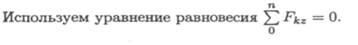В чем заключается допущение о сплошном строении материалов

Допущения и ограничения, принятые в сопротивлении материалов

Реальные строительные материалы, из которых воз­водятся различные здания и сооружения, представляют собой довольно сложные и неоднородные твердые тела, обладающие различными свойствами. Учесть это разно­образие свойств трудно, поэтому в сопротивлении мате­риалов используются не все характеристики твердых тел, а, только общие признаки, присущие всем телам суста­новившимися внутренними связями между ними. Иными словами, в сопротивлении материалов изучается поведе­ние конструкции из идеализированного материала, с со­хранением главных физико-механических характеристик.

1.1 Допущение о непрерывном (сплошном) строении материала.По этому допущению принимается, что весь объем любого элемента конструкции заполнен вещест­вом без каких-либо пустот, т. е. не учитывается действи­тельная дискретная атомистическая структура материа­лов. Это допущение позволяет выделять из любой части сооружения бесконечно малый элемент и, приписывая ему свойства материала всего сооружения, пользоваться при исследовании напряженно-деформированного состояния математическими методами анализа бесконечно малых величин.

2. Допущение о ненапряженном состоянии тела.Со­гласно этому допущению, в материале элемента до его нагружения нет никаких напряжений, т. е. действитель­ные (начальные) напряжения, характер и величина ко­торых зависят от причин возникновения, принимаются равными нулю. Иными словами, возникающие напряже­ния врезультате нагружения тела внешними силами принимаются за фактические напряжения в то время как они в действительности составляют лишь прирост напря­жение, вызванных этими силами.

3.Допущение об однородности материала. Согласно этому допущению принимается, что материал во всех точках любого объема имеет одинаковые физико-механи­ческие характеристики.

4.Допущение об изотропности материала. Согласно этому допущению, материал в любой точке и по всем на­правлениям, проведенным через эту точку, имеет одина­ковые физико-механические характеристики. Реальные материалы не являются абсолютно изотропными. Напри­мер, у технических сплавов стали физико-механические характеристики не одинаковы по разным направлениям, что обусловлено ее структурой и условиями обработки, но этими различиями обычно пренебрегают и считают сплавы стали изотропными. Если различия характерис­тик материала в разных направлениях будут значитель­ными, то такие конструкции следует рассчитывать по теории анизотропных тел. В данном случае материал наделяется свойствами абсолютной изотропии.

5.Допущение об идеальной упругости материала. Со­гласно этому допущению предполагается, что материал обладает способностью полностью восстанавливать свою первоначальную форму и размеры тела после устранения причин, вызвавших его деформацию. Деформация иде­ально упругого тела зависит лишь от тех нагрузок, ко­торые в данный момент действуют на тело и не зависят от того, каковы были нагрузки в предшествовавшие мо­менты времени. Данная гипотеза применима только при напряжениях, не превышающих предела упругости мате­риала.

6.Допущение о линейной зависимости между напря­жение и деформациями. Согласно этому допущению, упругое тело наделяется наиболее простой, а именно ли­нейной зависимостью между напряжениями и деформа­циями в данной точке, которая носит название закона Гука. Для такого материала диаграмма растяжения-сжатия, построенная в координатах «напряжение-де­формация», имеет вид наклонной прямой линии, прохо­дящей через начало координат. Для реальных материа­лов диаграмма имеет нелинейный характер, но на начальном этапе нагружения при сравнительно неболь­ших напряжениях, соответствующих действительной работе материала в конструкции, диаграмму с неболь­шой кривизной заменяют прямолинейной зависимостью Таким образом, в сопротивлении материалов закон Гука применим при напряжениях, не превосходящих некото­рого предела, называемого пределом пропорционально­сти. Если же исследуется поведение конструкции за пре­делом пропорциональности или же криволинейность диаграммы значительна, то расчеты проводят по физи­чески нелинейной теории.

7. Допущение о малости перемещений по сравнению с геометрическими размерами элементов сооружений. Со­гласно этому допущению, не учитываются изменения геометрических размеров элементов и местоположения нагрузок из-за искривления, растяжения, сжатия и сдви­га после приложения к ним внешних сил. Поскольку в со­противлении материалов исследуются элементы в виде бруса, то сравнение перемещений производится с его длиной. Таким образом, реакции и внутренние силовые факторы определяются по заданной, начальной геомет­рии, что значительно упрощает расчет, так как все урав­нения приобретают линейный вид. В тех же случаях, когда перемещения сравнимы с длинами элементов, рас­чет следует производить по деформированной схеме, пользуясь геометрически нелинейной теорией.

8. Следствием трех последних допущений об идеаль­ной упругости материала, линейной зависимости между напряжениями и деформациями и малости перемещений является принцип независимости действия сил или прин­цип суперпозиции.

9. Гипотеза плоских сечений (гипотеза Бернулли). Со­гласно этой гипотезе, поперечное сечение элемента (бал­ки, стержня), плоское и перпендикулярное к его оси до приложения к элементу внешних сил, остается плоским и перпендикулярным к оси и после приложения к эле­менту нагрузок.

10. Гипотеза Сен-Венана. Согласно этой гипотезе, в достаточно удаленных точках элемента от места приложения нагрузки внутренние силовые факторы весьма мало зависят от способа приложения этой нагрузки.

Источник

Допущения сопромата

При построении теории расчета на прочность, жесткость и устойчивость принимаются допущения, связанные со свойствами материалов и с деформацией тела.

Допущения, связанные со свойствами материалов

Сначала рассмотрим допущения, связанные со свойствами материалов :

допущение 1 : материал считается однородным (его физико-механические свойства считаются одинаковыми во всех точках;

допущение 2 : материал полностью заполняет весь объем тела, без каких-либо пустот (тело рассматривается как сплошная среда). Это допущение дает возможность применять при исследовании напряженно-деформированного состояния тела методы дифференциального и интегрального исчислений, которые требуют непрерывности функции в каждой точке объема тела;

допущение 3 : материал изотропный, то есть его физико-механические свойства в каждой точке одинаковы во всех направлениях. Анизотропные материалы – физико-механические свойства которых изменяются в зависимости от направления (например, дерево);

допущение 4 : материал является идеально упругим (после снятия нагрузки все деформации полностью исчезают).

Допущения, связанные с деформацией

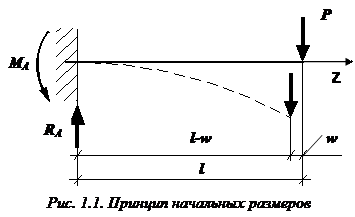
допущение 1 : деформации считаются малыми. Из этого допущения следует, что при составлении уравнений равновесия, а также при определении внутренних сил можно не учитывать деформацию тела. Это допущение иногда называют принципом начальных размеров. Например, рассмотрим стержень, заделанный одним концом в стену и нагруженный на свободном конце сосредоточенной силой (рис. 1.1).

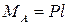
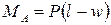
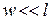
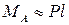
Момент в заделке, определенный из соответствующего уравнения равновесия методом теоретической механики, равен: . Однако прямолинейное положение стержня не является его положением равновесия. Под действием силы (P) стержень изогнется, и точка приложения нагрузки сместится и по вертикали, и по горизонтали. Если записать уравнение равновесия стержня для деформированного (изогнутого) состояния, то истинный момент, возникающий в заделке, окажется равным: . Принимая допущение о малости деформаций, мы полагаем, что перемещением (w) можно пренебречь по сравнению с длиной стержня (l), то есть , тогда . Допущение возможно не для всех материалов.

допущение 2 : перемещения точек тела пропорциональны нагрузкам, вызывающим эти перемещения (тело является линейно деформируемым). Для линейно деформируемых конструкций справедлив принцип независимости действия сил ( принцип суперпозиции ): результат действия группы сил не зависит от последовательности нагружения ими конструкции и равен сумме результатов действия каждой из этих сил в отдельности. В основе этого принципа лежит также предположение об обратимости процессов нагрузки и разгрузки.

Источник

Основные гипотезы сопротивления материалов

Основными гипотезами сопротивления материалов называют следующие:

Гипотеза об однородности и сплошности материала

допущение об однородности и непрерывности материала, т. е. принимают, что свойства материала не зависят от формы и размеров тела и одинаковы во всех его точках; Сплошность материала также равномерна. Нет ни включений ни раковин ни «непроваров»

Эта гипотеза позволяет упростить расчеты и выводы формул сопротивления материалов, т.к. идеализирует объект расчета, не учитывая реальные дефекты без которых невозможно изготовить реальные элементы конструкции.

Когда варится сталь или другой материал не возможно изготовить идеальную смесь и идеально остудить этот материал так, чтобы внутри не возникло неоднородности. Она есть, минимальная, но есть. И сопротивление материалов это не учитывает. Компенсировать эту погрешность мы будем с помощью коэффициента запаса.

В реальной жизни все тела имеют дефекты и несплошности. Но чтобы иметь возможность рассчитывать элементы конструкции, сопротивление материалов, при выводе всех своих формул использует идеализацию объекта и говорит, что тело однородное и сплошное по всему объему.

Гипотеза о малости деформаций

допущение о малости рассматриваемых перемещений. Предполагается, что перемещения, возникающие в конструкции в результате ее деформации, настолько малы, что по сравнению с размерами элементов ими можно пренебречь;

Например длина балки имеет рамер 4 метра, вес, кторый перемещается по ней вызовет максимальный прогиб 4 мм. Ну а в опорах возникнут реакции, которые конечно будут воздействовать на них, но эта величина деформаций опор будет на столько малой, что мы ней пренебрегаем при расчете балки.

Гипотеза об идеальной упругости материала

идеальная упругость материала принимается при расчетах всех видов деформаций и работы конструкций

Упругими мы называем такие деформации, которые после снятия нагрузки полностью снимаются с элемента конструкции. Т.е. объект полностью восстанавливает свою форму после снятия нагрузки. В реальной жизни это не совсем так. Тем более есть разные материалы и они по разному «упруги». Но при расчетах в формулах сопротивления материалов эту не идеальность не учитывают.

после того как слон сойдет с этой балки она станет снова ровной, идеально ровной

Предполагают, что материал обладает способностью полностью восстанавливать первоначальные размеры и форму после устранения нагрузок. Это допущение справедливо при ограниченных нагрузках. После некоторого уровня нагрузок в материале возникают остаточные деформации, не исчезающие после удаления нагрузки;

После приложения нагрузки, в зависимости от ее величины объект, тело может полностью восстановится и может восстанавливаться не на 100% (сейчас речь только об упругих деформациях). Так вот восстановление после снятия нагрузки в пределах упругих деформаций считается в сопротивлении материалов 100%, т.е. идеальным. Что конечно же в реальной жизни не наблюдается. Но это нужно для введения законов, которые позволили бы производить расчеты.

Гипотеза о линейной зависимости между силами и перемещениями

Допущение о линейной зависимости между силами, действующими на конструкцию, и вызываемыми ими перемещениями.

Согласно этому допущению величины упругих перемещений, возникающих в конструкции, прямо пропорциональны величинам вызвавших их сил. Т.е. перемещение пропорционально силе.

Пропорциональность между силой и изменением размера объекта сильно зависит от материала из которого он изготовлен. Так у стали хорошо заметна линия пропорциональности, на которой этот закон соблюдается. Об этом в Более мягкие материалы имеют линию не прямую, а больше криволинейную форму. Но сопротивление материалов этими нюансами пренебрегает, и ведет пересчет на прямолинейную форму. От нее уже и отталкиваются в дальнейших расчетах.

Принцип независимости действия сил

Допущение, называемое принципом независимости действия сил или принцип суперпозиции. Согласно этому принципу, результат воздействия на сооружение системы нагрузок, приложенных одновременно, равен сумме результатов воздействия тех же нагрузок, прикладываемых к телу по отдельности.

Использование принципа независимости действия сил возможно при условии соблюдения допущений малости деформаций и идеальной упругости;

Гипотеза плоских сечений или гипотеза Бернули

Допущение, именуемое гипотезой плоских сечений (Я. Бернулли), на основании которой предполагают, что плоские поперечные сечения, проведенные в брусе до деформации, остаются плоскими и нормальным, и к продольной оси и после деформации после приложения нагрузки.

сечения плоские до деформации остаются плоскими и после приложения нагрузки

Напряжение в сопротивлении материалов что это

Напряжение в сопротивлении материалов это мера которая позволят оценить величину действия нагрузки на единицу сопротивляемости этой силе. При растяжении-сжатии это площадь сечения, а при изгибе — момент инерции. Напряжение действует по площади очень маленькой площадки, из которых складывается сопротивление всей площади елемента конструкции.

При этом для разных материалов экспериментально определены максимальные величины этих напряжений. Так называемые допустимые напряжения. Подробнее об этом в статье испытания стали на разрыв.

Таким образом рассчитав напряжение в элементе конструкции мы можем подобрать материал, который выдержит расчетное напряжение или ответить на сколько близок элемент конструкции из заданного материала к допустимому напряжению.

Величина напряжений в каждой точке является мерой внутренних сил, которые возникают в материале как результат деформации, вызванной внешней силой.

Немного о нашем сайте:

Пройти курсы по сопротивлению материалов, получить короткие и емкие уроки для подготовки к экзамену студентам или инженеру вспомнить, улучшить уровень подготовки по отдельным темам? Это легко! С Александром Заболотным!

Кроме обучения сопротивлению материалов предлагаю получить знания и навыки решения задач по строительной механике.

Видео канал со снятыми видео уроками по сопротивлению материалов и строительной механике вы найдете по следующей ссылке.

Список видео уроков последовательно один за другим, где я рассказываю о сопротивлении материалов вы найдете по следующей ссылке:

Приветственное видео канала, для того чтобы познакомиться и подписаться, чтобы не пропустить новые видео уроки предлагаю ниже:

Источник

Расчетов в сопротивлении материалов

Механические свойства материалов

Прочность — способность не разрушаться под нагрузкой. Жесткость — особность незначительно деформироваться под нагрузкой.

Тема 2.1. Основные положения 163

Выносливость — способность длительное время выдерживать переменные нагрузки.

Устойчивость — способность сохранять первоначальную фор­му упругого равновесия.

Вязкость — способность воспринимать ударные нагрузки.

Виды расчетов

Расчет на прочность обеспечивает неразрушение конструкции.

Расчет на жесткость обеспечивает деформации конструкции под нагрузкой в пределах допустимых норм.

Расчет на выносливость обеспечивает необходимую долговеч­ность элементов конструкции.

Расчет на устойчивость обеспечивает сохранение необходимой формы равновесия и предотвращает внезапное искривление длинных стержней.

Основные гипотезы и допущения

Приступая к расчетам конструкции, следует решить, что в дан­ном случае существенно, а что можно отбросить, т. к. решение тех­нической задачи с полным учетом всех свойств реального объекта невозможно.

Допущения о свойствах материалов

Материалы однородные — в любой точке материалы имеют оди­наковые физико-механические свойства.

Материалы представляют сплошную среду — кристаллическое строение и микроскопические дефекты не учитываются.

Материалы изотропны — механические свойства не зависят от направления нагружения.

Материалы обладают идеальной упругостью — полностью вос­станавливают форму и размеры после снятия нагрузки.

В реальных материалах эти допущения выполняются лишь от­части, но принятие таких допущений упрощает расчет. Все упроще­ния принято компенсировать, введя запас прочности.

Допущения о характере деформации

Все материалы под нагрузкой деформируются, т. е. меняют форму и размеры.

Характер деформации легко проследить при испытании мате­риалов на растяжение.

Перед испытаниями цилиндрический образец закрепляется в за­хватах разрывной машины, растягивается и доводится до разруше­ния. При этом записывается зависимость между приложенным уси­лием и деформацией. Получают график, называемый диаграммой растяжения. Для примера на рис. 18.1 представлена диаграмма ра­стяжения малоуглеродистой стали.

На диаграмме отмечают особые точки:

— от точки 0 до точки 1 — прямая линия (деформация пря­мо пропорциональна нагрузке);

— от точки 2 до точки 5 деформации быстро нарастают и образец разрушается, разрушению предшествует появление утончения (шейки) в точке 4.

Если прервать испытания до точки 2, образец вернется к исходным размерам; эта область называется областью упругих де­формаций. Упругие деформации полностью исчезают после снятия нагрузки.

При продолжении испытаний после точки 2 образец уже не воз­вращается к исходным размерам, деформации начинают накапли­ваться.

При выключении машины в точке А образец несколько сжима­ется по линии АВ, параллельной линии 01. Деформации после точки 2 называются пластическими, они полностью не исчезают; сохра­нившиеся деформации называются остаточными.

На участке 01 выполняется закон Гука:

В пределах упругости деформации прямо пропорциональны на­грузке.

Считают, что все материалы подчиняются закону Гука.

Тема 2.1. Основные положения 165

нагрузкой не изменяются.

Расчеты ведут, используя принцип начальных размеров. При ра­боте конструкции деформации должны оставаться упругими.

К нарушению прочности следует относить и возникновение пла­стических деформаций. Хотя в практике бывают случаи, когда мест­ные пластические деформации считаются допустимыми.

Классификация нагрузок и элементов конструкции

Классификация нагрузок

Статистические нагрузки (рис. 18.2а) не меняются со време­нем или меняются очень медленно. При действии статистических нагрузок проводится расчет на прочность.

Повторно-переменные нагрузки (рис. 18.26) многократно меня­ют значение или значение и знак. Действие таких нагрузок вызывает усталость металла.

Динамические нагрузки (рис. 18.2в) меняют свое значение в короткий промежуток времени, они вызывают большие ускоре­ния и силы инерции и могут привести к внезапному разрушению конструкции.

Из теоретической механики известно, что по способу приложе­ния нагрузки могут быть сосредоточенными или распределенными по поверхности.

Реально передача нагрузки между деталями происходит не в точке, а на некоторой площадке, т.е. нагрузка является распреде­ленной.

Однако если площадка контакта пренебрежительно мала по сравнению с размерами детали, силу считают сосредоточенной.

При расчетах реальных деформируемых тел в сопротивлении материалов заменять распределенную нагрузку сосредоточенной не следует.

Аксиомы теоретической механики в сопротивлении материалов используются ограниченно.

Нельзя переносить пару сил в другую точку детали, переме­щать сосредоточенную силу вдоль линии действия, нельзя систе­му сил заменять равнодействующей при определении перемещений. Все вышеперечисленное меняет распределение внутренних сил в конструкции.

Формы элементов конструкции

Все многообразие форм сводится к трем видам по одному при­знаку.

1. Брус — любое тело, у которого длина значительно больше других размеров.

В зависимости от форм продольной оси и поперечных сечений различают несколько видов брусьев:

— прямой брус постоянного поперечного сечения (рис. 18.3а);

Тема 2.1. Основные положения 167

3. Массив — тело, у которого три размера одного порядка.

Контрольные вопросы и задания

1. Что называется прочностью, жесткостью, устойчивостью?

2. По какому принципу классифицируют нагрузки в сопроти­влении материалов? К какому виду разрушений приводят повторно-переменные нагрузки?

3. Какие нагрузки принято считать сосредоточенными?

4. Какое тело называют брусом? Нарисуйте любой брус и ука­жите ось бруса и его поперечное сечение. Какие тела называют пла­стинами?

5. Что называется деформацией? Какие деформации называют упругими?

6. При каких деформациях выполняется закон Гука? Сформули­руйте закон Гука.

7. Что такое принцип начальных размеров?

8. В чем заключается допущение о сплошном строении матери­алов? Поясните допущение об однородности и изотропности матери­алов.

Тема 2.1. Основные положения.

Нагрузки внешние и внутренние,

Знать метод сечений, внутренние силовые факторы, соста­вляющие напряжений.

Уметь определять виды нагружений и внутренние силовые факторы в поперечных сечениях.

Элементы конструкции при работе испытывают внешнее воз­действие, которое оценивается величиной внешней силы. К внешним силам относят активные силы и реакции опор.

Под действием внешних сил в детали возникают внутренние силы упругости, стремящиеся вернуть телу первоначальную форму и размеры.

Внешние силы должны быть определены методами теоретиче­ской механики, а внутренние определяются основным методом со­противления материалов — методом сечений.

В сопротивлении материалов тела рассматриваются в равнове­сии. Для решения задач используют уравнения равновесия, получен­ные в теоретической механике для тела в пространстве.

Используется система координат, связанная с телом. Чаще про­дольную ось детали обозначают z, начало координат совмещают с левым краем и размещают в центре тяжести сечения.

Метод сечений

Метод сечений заключается в мысленном рассечении тела плоскостью и рассмотрении равновесия любой из отсеченных ча­стей.

Если все тело находится в равновесии, то и каждая его часть находится в равновесии под действием внешних и внутренних сил. Внутренние силы определяются из уравнений равновесия, соста­вленных для рассматриваемой части тела.

Рассекаем тело поперек плоскостью (рис. 19.1). Рассматрива­ем правую часть. На нее действуют внешние силы F4 ; F5 ; F6 и внутренние силы

Тема 2.1. Основные положения 169

упругости qk, распределенные по сечению. Систему распределенных сил можно заменить главным вектором Rq, поме­щенным в центр тяжести сечения, и суммарным моментом сил Mo :

Разложив главный вектор Rо по осям, получим три составляющие:

где N_z — продольная сила;

Q_x — поперечная сила по оси х;

Q_y — поперечная сила по оси у.

Главный момент тоже принято представлять в виде моментов пар сил в трех плоскостях проекции:

М_х — момент сил относительно Ох; М_у — момент сил относитель­но Оу; M_z — момент сил относительно Oz.

Полученные составляющие сил упругости носят название вну­тренних силовых факторов. Каждый из внутренних силовых фак­торов вызывает определенную деформацию детали. Внутренние си­ловые факторы уравновешивают приложенные к этому элементу де­тали внешние силы. Используя шесть уравнений равновесия, можно получить величину внутренних силовых факторов:

Из приведенных уравнений следует, что:

N_z — продольная сила, равная алгебраической сумме проекций на ось Oz внешних сил, действующих на отсеченную часть бруса; вызывает растяжение или сжатие;

Q_x — поперечная сила, равная алгебраической сумме проекций на ось Qx внешних сил, действующих на отсеченную часть;

Q_y — поперечная сила, равная алгебраической сумме проекций на ось Оу внешних сил, действующих на отсеченную часть;

М_г — крутящийся момент, равный алгебраической сумме мо­ментов внешних сил относительно продольной оси Oz; вызывает скручивание бруса;

М_х — изгибающий момент, равный алгебраической сумме мо­ментов внешних сил относительно оси Ох;

М_у — изгибающий момент, равный алгебраической сумме мо­ментов внешних сил относительно оси Оу;

моменты М_х и М_у вызывают изгиб бруса в соответствующей плоскости.

Напряжения

Метод сечений позволяет определить величину внутреннего си­лового фактора в сечении, но не дает возможности установить за­кон распределения внутренних сил по сечению. Для оценки прочно­сти необходимо определить величину силы, приходящуюся на любую точку поперечного сечения.

Величину интенсивности внутренних сил в точке поперечного сечения называют механическим напряжением. Напряжение харак­теризует величину внутренней силы, приходящейся на единицу пло­щади поперечного сечения.

Тема 2.1. Основные положения 171

Рассмотрим брус, к которому приложена внешняя нагрузка (рис. 19.2). С помощью метода сечений рассечем брус поперечной плоскостью, отбросим левую часть и рассмотрим равновесие остав­шейся правой части. Выделим на секущей плоскости малую площадку ΔА На этой площадке действует равнодействующая внутренних сил упругости. Направление напряжения р_ср совпадает с направлением внутренней силы в этом сече­нии.

Вектор р_ср называют полным напряжени­ем. Его принято раскладывать на два вектора (рис. 19.3): τ — лежащий в площадке сечения и σ — направленный перпендикулярно площад­ке.

Если вектор р — пространственный, то его раскладывают на три составляющие:

Нормальное напряжение характеризует сопротивление сечения растяжению или сжатию.

Касательное напряжение характеризует сопротивление сечения сдвигу.

Сила N (продольная) вызывает появление нормального напря­жения а. Силы Q_x и Q_y вызывают появление касательных напря­жений т. Моменты изгибающие М_х и М_у вызывают появление нор­мальных напряжений ст, переменных по сечению.

Крутящий момент M_z вызывает сдвиг сечения вокруг продоль­ной оси, поэтому появляются касательные напряжения т.

Примеры решения задач

Пример 1.Определить величину продольной силы в сечении 1-1 (рис. 19.4).

Решение

Величина продольной силы в сечении не зависит от того, какая часть бруса рассматривается.

Пример 2.Определить внутренний силовой фактор в сечении 1-1 (рис. 19.5а).

Решение

Контрольные вопросы и задания

1. Какие силы в сопротивлении материалов считают внешними?
Какие силы являются внутренними?

2. Какими методами определяют внешние силы? Как называют
метод для определения внутренних сил?

3. Сформулируйте метод сечений.

Тема 2.1. Основные положения 173

4. Как в сопротивлении материалов располагают систему коор­динат?

5. Что в сопротивлении материалов называют внутренними си­ловыми факторами? Сколько в общем случае может возникнуть вну­тренних силовых факторов?

6. Запишите систему уравнений, используемую при определении внутренних силовых факторов в сечении?

7. Как обозначается и как определяется продольная сила в сече­нии?

8. Как обозначаются и как определяются поперечные силы?

9. Как обозначаются и определяются изгибающие и крутящий моменты?

10. Какие деформации вызываются каждым из внутренних си­ловых факторов?

11. Что называют механическим напряжением?

12. Как по отношению к площадке направлены нормальное и касательные напряжения? Как они обозначаются?

13. Какие напряжения возникают в поперечном сечении при дей­ствии продольных сил?

14. Какие напряжения возникают при действии поперечных сил?

15. С помощью метода сечений определите величину внутрен­него силового фактора в сечении 1-1 и вид нагружения (рис. 19.6).

16. С помощью метода сечений определите величину момента
m4, величину внутреннего силового фактора в сечении 2-2 и вид
нагружения (рис. 19.7).

17. Ответьте на вопросы тестового задания.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Источник