В чем заключается гидростатический парадокс

08.10.202309.07.2022 admin 0 Comments

Гидростатический парадокс

Смотреть что такое «Гидростатический парадокс» в других словарях:

ГИДРОСТАТИЧЕСКИЙ ПАРАДОКС — вес жидкости, налитой в сосуд, может отличаться от силы давления, оказываемой ею на дно сосуда. Так, в расширяющихся кверху сосудах сила давления на дно меньше веса жидкости, а в суживающихся больше. В цилиндрическом сосуде обе силы одинаковы.… … Большой Энциклопедический словарь

ГИДРОСТАТИЧЕСКИЙ ПАРАДОКС — заключается в том, что вес жидкости, налитой в сосуд, может отличаться от силы давления, оказываемой ею на дно сосуда. Так, в расширяющихся кверху сосудах (рис.) сила давления на дно меньше веса жидкости, а в суживающихся больше. В цилиндрич.… … Физическая энциклопедия

Гидростатический парадокс — Гидростатический парадокс явление, при котором вес налитой в сосуд жидкости может отличаться от силы давления на дно. Причины Схема опыта Паскаля Причина гидростатического парадокса состоит в том, что жидкость дав … Википедия

ГИДРОСТАТИЧЕСКИЙ ПАРАДОКС — физич. закон, в силу которого давление на дно в сосудах различной формы, но с одинаковой величины дном, наполнен. одною и тою же жидкостью до одинаковой высоты, одинаково, не смотря на разницу в количестве жидкости. Словарь иностранных слов,… … Словарь иностранных слов русского языка

гидростатический парадокс — вес жидкости, налитой в сосуд, может отличаться от силы давления жидкости на дно сосуда. Так, в расширяющихся кверху сосудах (рис.) сила давления на дно меньше веса жидкости, а в суживающихся больше. В цилиндрическом сосуде обе силы одинаковы.… … Энциклопедический словарь

ГИДРОСТАТИЧЕСКИЙ ПАРАДОКС — вес жидкости, налитой в сосуд, может отличаться от силы давления жидкости на дно сосуда. Так, в расширяющихся кверху сосудах (рис.) сила давления на дно меньше веса жидкости, а в суживающихся больше. В цилиндрич. сосуде обе силы одинаковы.… … Естествознание. Энциклопедический словарь

гидростатический парадокс — hidrostatinis paradoksas statusas T sritis fizika atitikmenys: angl. hydrostatic paradox vok. hydrostatisches Paradoxon, n rus. гидростатический парадокс, m pranc. paradoxe hydrostatique, m … Fizikos terminų žodynas

Гидростатический парадокс — см. Гидростатическое давление … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Основной закон гидростатики — (закон Паскаля) формулируется так Давление, оказываемое на жидкость(или газ) в каком либо одном месте на ее границе, например, поршнем, передается без изменения во все точки жидкости(или газа). Закон назван в честь французского учёного Блеза… … Википедия

Источник

В чем состоит гидростатический парадокс?

Гидростатический парадокс, заключается в том, что вес жидкости, налитой в сосуд, может отличаться от силы давления, оказываемой ею на дно сосуда. Так, в расширяющихся кверху сосудах сила давления на дно меньше веса жидкости, а в суживающихся – больше. В цилиндрическом сосуде обе силы одинаковы. Если одна и та же жидкость налита до одной и той же высоты в сосуды разной формы, но с одинаковой площадью дна, то, несмотря на различный вес налитой жидкости, сила давления на дно одинакова для всех сосудов и равна весу жидкости в цилиндрическом сосуде. Это следует из того, что давление покоящейся жидкости зависит только от глубины под свободной поверхностью и от плотности жидкости. Объясняется гидростатический парадокс следующим. Поскольку гидростатическое давление всегда нормально к стенкам сосуда, сила давления на наклонные стенки имеет вертикальную составляющую, которая компенсирует вес излишнего против цилиндра объема жидкости в расширяющемся кверху сосуде и вес недостающего против цилиндра объема жидкости в суживающемся кверху сосуде. Гидростатический парадокс обнаружил французский физик Блез Паскаль (1623–1662).

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

ГИДРОСТАТИЧЕСКИЙ ПАРАДОКС

Полезное

Смотреть что такое «ГИДРОСТАТИЧЕСКИЙ ПАРАДОКС» в других словарях:

Гидростатический парадокс — заключается в том, что вес жидкости, налитой в сосуд, может отличаться от силы давления, оказываемой ею на дно сосуда. Так, в расширяющихся кверху сосудах (рис.) сила давления на дно меньше веса жидкости, а в суживающихся больше. В… … Большая советская энциклопедия

Источник

Гидростатический парадокс и сила давления на стенку

Понятие гидростатический парадокс является одним из основных в динамике жидкостей. Для того чтобы разобраться о чем идет речь необходимо вспомнить формулировку закона Паскаля.

Закон Паскаля: внешнее давление, создаваемое в любой точке покоящейся жидкости, передается одинаково по всему объему (во всех направлениях).

В этой статье мы расскажем о том как прийти к обоснованию и вообще, что из себя представляет гидростатический парадокс, как увидеть его на примере опыта, где он нашел применение и конечно, какие выводы можно сделать из полученных знаний.

Содержание статьи

Вывод расчетной формулы

Определим полную силу давления Р на плоскую наклонную стенку, имеющую площадь F. Линия Oz является следом плоскости рассматриваемой стенки.

Чтобы сделать видимым контур поверхности стенки F, на которую действует сила P, повернем рассматриваемую плоскость вокруг оси Oz до совпадения её с плоскостью чертежа. Тогда ось Ox будет представлять собой след свободной поверхности жидкости при пересечении её с плоскостью стенки.

Рассмотрим прямоугольную элементарную площадку dF, заштрихованную на чертеже, стороны которой параллельны Ox.

Обозначим расстояние площадки dF от оси Ox буквой l, а глубину погружения её под уровень жидкости через h.

Расстояние центра тяжести С рассматриваемой площадки от оси Ox обозначим l_ц.т. (расстояние центра тяжести), а глубину погружения его под уровень h_ц.т.

h = l × sinα и hц.т. = l_ц.т. × sinα (формула 1)

где α – угол наклона стенки к горизонту.

Далее вычисляем элементарную силу давления dP. Для этого вспоминаем:

1) закон Паскаля (описан в первом абзаце статьи) дает выражение

2) сила давления, действующая на какую либо элементарную поверхность, определяется выражением

Объединяя выражения под пунктом 1 и 2 получаем:

dP = (p₀ + ρ × g × h) × dF (формула 2)

Затем подставим в полученную формулу 2 значение h из формулы 1 и проинтегрируем левую и правую часть формулы 2 по всей площади стенки F и получим формулу 3

Величина интеграла ldF представляет собой статический момент площади относительно оси Ox. Он равен произведению площади F на расстояние от её центра тяжести до оси, относительно которой берется статический момент.

Далее подставляя этот статический момент в формулу 3 получим

P = (p₀ + ρ × g × h_ц.т.) × *F (формула 4)

Следовательно, полная сила давления в жидкости на какую-либо плоскую стенку равна произведению площади стенки на гидростатическое давление в её центре тяжести.

Формула 4 для определения силы давления на плоскую стенку действительна для случая, когда внешнее давление над поверхностью жидкости в сосуде равно p₀.

Если сосуд открыт, то p₀ = p_атм (равно атмосферному давлению), тогда зависимость, описанная в формуле 4, определяет силу, обусловленную полным абсолютным давлением жидкости на плоскость.

Сила, обусловленная избыточным давлением на плоскость, в этом случае записывается так

P = ρ × g × h_ц.т. × F (формула 5)

Это наиболее часто встречающийся на практике случай.

Сущность гидростатического парадокса

Зависимость описанная в формуле 5 представляет собой так называемый гидростатический парадокс.

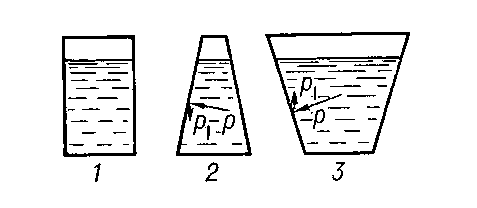
Для его иллюстрации посмотрите представленный рядом рисунок.

Гидростатический парадокс заключается в том, что давление, оказываемое на дно, не зависит от формы сосуда при условии соблюдения следующих условий:
1. дно сосудов различной формы имеет одинаковую площадь и расположено горизонтально;
2. высота уровня жидкости и её плотность в различных сосудах одинакова.

Для наглядного примера демонстрации гидростатического парадокса представьте три сосуда различной формы заполненные водой.

В сосуд А налита вода весом 4 Н (Ньютона), в сосуд В налита вода весом 3 Н и в сосуд С вода весом 2 Н.

Высотная отметка до которой налита вода в каждом сосуде одинакова и составляет 0,5 метра. Площадь дна у всех трех сосудов тоже одинакова и составляет 30 см = 0,003 м 2 = S.

Используя формулу Паскаля

где ρ – плотность воды (округлим до 1000 кг/см 2 );
g – ускорение свободного падения (округляем до 10 м/с 2 );
h – высота до которой налита вода (в нашем примере 0,5м).

p = 1000 × 10 × 0,5 = 5000 Па.

Тогда сила действующая на дно сосуда

F = p × S = 5000 × 0,003 = 15 Н.

Таким образом жидкость в каждом сосуде независимо и с весом 4 Н для сосуда А и с весом 2 Н для сосуда С давит на дно с одинаковой силой равной 15 Н.

Кажет это противоречит здравому смыслу, но приводит к интересным опытам, которые ставил Блез Паскаль

Гидростатический парадокс и опыт Паскаля

Пытаясь найти объяснение гидростатического парадокса Паскаль ставил сосуды, заполненные водой на специальные весы, которые позволяют замерить силу которая давит на дно каждого из сосудов.

Проведя множество замеров ученый пришел к выводу, что при определенной форме сосуда возможно даже с помощью небольшого количества жидкости создать очень большую силу.

Своё умозаключение Блез Паскаль в 1648 году продемонстрировал на примере опыта с бочкой.

Затем он поднялся на второй этаж – на высоту около 4 метров и налил в трубку кружку воды.

Возникшие в трубке силы создали такое давление на крышку бочки, что её разорвало.

Воды из кружки, которую ученый вылил в трубку поднялась до отметки 4 метра. Таким образом вес воды составил

Явление гидравлического парадокса нашло применение в современной техники. Оно широко используется в современных гидравлических прессах.

Источник

В чем заключается гидростатический парадокс

Гидростатический парадокс — явление, при котором сила весового давления налитой в сосуд жидкости на дно сосуда может отличаться от веса налитой жидкости. В сосудах с увеличивающихся к верху поперечным сечением сила давления на дно сосуда меньше веса жидкости, в сосудах с уменьшающимся к верху поперечным сечением сила давления на дно сосуда больше веса жидкости. Сила давления жидкости на дно сосуда равно весу жидкости лишь для сосуда цилиндрической формы.

Сила давления жидкости на горизонтальное дно сосудов не зависит от их формы.

Причина гидростатического парадокса состоит в том, что жидкость давит не только на дно, но и на стенки сосуда. Давление жидкости на наклонные стенки имеет вертикальную составляющую. В расширяющемся к верху сосуде она направлена вниз, в сужающемся к верху сосуде она направлена вверх. Вес жидкости в сосуде будет равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда. Если одна и та же жидкость налита до одной и той же высоты в сосуды разной формы, но с одинаковой площадью дна, то, несмотря на различный вес налитой жидкости, сила давления на дно одинакова для всех сосудов и равна весу жидкости в цилиндрическом сосуде. Это следует из того, что давление покоящейся жидкости зависит только от глубины под свободной поверхностью и от плотности жидкости.

Источник

Портал agro-sss.ru

В чем заключается гидростатический парадокс

Гидростатический парадокс

Смотреть что такое «Гидростатический парадокс» в других словарях:

В чем состоит гидростатический парадокс?

Читайте также

Бернадетт Субиру, парадокс из Лурда

Парадокс: холодные звезды

Парадокс

Парадокс в музыке

Цитата. Афоризм. Парадокс

Парадокс и банальность

ПАРАДОКС