В чем заключается опыт юнга

В чем заключается опыт юнга

1. Какие два взгляда на природу света существовали с давних пор среди ученых?

До начала XIX в. не было доказательств ни в пользу волновых, ни в пользу корпускулярных представлений.

В настоящее время признана справедливой как волновая, так и корпускулярная теория.
Обе теории, дополняя друг друга, позволяют объяснять многие физические явления.

2. В чем заключалась суть опыта Юнга, что этот опыт доказывал и когда был поставлен?

В 1802 г. английский ученый Томас Юнг поставил опыт по сложению пучков света от двух источников, в результате чего получил не меняющуюся во времени картину, состоящую из чередующихся светлых и темных полос.
Юнг правильно объяснил возникновение полос интерференцией света.

Однако интерференция присуща только волновым (т. е. периодическим) процессам.
Поэтому oпыт Юнга стал доказательством того, что свет обладает волновыми свойствами.

3. В чем заключается интерференция звуковых волн?

При наложении двух когерентных волн (т. е. волн с одинаковой частотой и постоянной разностью фаз) образуется так называемая интерференционная картина, т. е. не меняющаяся со временем картина распределения амплитуд колебаний в пространстве.

В одних точках пространства колебания всегда происходят с максимальной амплитудой.
Это те точки, в которые колебания от обоих источников в любой момент времени приходят в одинаковых фазах и поэтому всегда усиливают друг друга.
В других точках колебания происходят с минимальной амплитудой.
Эти точки расположены по отношению к источникам так, что к ним колебания всегда приходят в противоположных фазах, ослабляя друг друга (а при равных амплитудах колебаний волны в любой момент времени полностью гасят друг друга).
В остальных точках колебания также происходят с постоянными амплитудами, значения которых лежат в промежутке от минимальной до максимальной.

4. Как на опыте можно получить интерференционную картину света?

На проволочное кольцо с ручкой, затянутое мыльной пленкой, в затемненном помещении направляется свет желтого цвета.
На пленке образуются горизонтально расположенные чередующиеся желтые и черные полосы.

5. Как объяснить появление на мыльной пленке чередующихся полос?

Свет, падая на пленку, частично отражается от передней поверхности в точке А, а частично проходит внутрь пленки и отражается от задней поверхности в точке В, после чего выходит из пленки в точке С.
Волны, выходящие из точек A и C, являются когерентными, т,к. они образуются от одного и того же источника.
Разность хода длин волн зависит от толщины пленки, которая в разных точках различна.
Если толщина пленки окажется такой, что волны будут выходить из точек А и С, имея одинаковые фазы, то эти волны при сложении усилят друг друга.
В результате возникнет максимум интерференционной картины — желтая полоса.
Если толщина пленки окажется такой, что волны будут выходить из точек А и С в противоположных фазах, то эти волны при сложении будут гасить друг друга.
В результате возникнет минимум интерференционной картины — темная полоса.

6. Что доказывает опыт с освещением мыльной пленки?

Этот опыт доказывает, что раз наблюдается явление интерференции, значит, свет обладает волновыми свойствами.

7. Что можно сказать о частоте (или длине волны) световых волн разных цветов?

Томас Юнг измерил еще и длину световой волны.
Оказалось, что свету разных цветов соответствуют волны разной длины (разной частоты).

Например, красному свету в световом диапазоне соответствует самая большая длина волны ( иначе самая маленькая частота).
Длины волн убывают (а частоты возрастают) в следующей последовательности цветов: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.

Источник

Эксперимент с двумя щелями и границы макромира

В 1900, последнем году XIX века, Макс Планк открыл кванты света: показал, что энергия света передается в виде минимальных энергетических пакетов. Так зародилась квантовая физика, которая, казалось бы, совершенно случайно попала из XXI века в начало XX-го. На практике квантовая механика оказалась одной из самых точных и строгих систем, известных науке: принципы квантовой механики лежат в основе деления атомного ядра, действия лазера, работы полупроводников. Сегодня уже осуществлены квантовая телепортация и квантовые вычисления. При этом, еще в 1927 году, на пятом Сольвеевском конгрессе, посвященном проблемам квантовой механики, состоялся знаменитый спор между Альбертом Эйнштейном и Нильсом Бором по поводу интерпретируемости квантовой механики. На тот момент победила точка зрения Бора («копенгагенская интерпретация»), указывающая, что следует абстрагироваться от концептуализации событий, происходящих при квантовых взаимодействиях, удовлетворившись математической согласованностью квантовой механики. При этом квантовая система понимается во многом как «черный ящик», но ее уравнения с удивительной точностью подтверждают результаты экспериментов.

Основное отличие квантовой физики (доминирует в микромире) от классической физики (доминирует в макромире) заключается в вероятностном характере квантовых процессов. Так, применительно к электрону в атоме, уравнения квантовой механики дают распределение вероятностей, указывающих, в какой точке орбитали должен быть электрон – и именно там он и оказывается по результатам эксперимента.

Именно с неопределенностью результатов квантового эксперимента вплоть до его окончания связаны и разнообразные квантовые парадоксы, увлекательно описанные в книге Николя Жизана «Квантовая случайность». С неопределенностью того же рода связан знаменитый реальный эксперимент с двумя щелями. Ниже я напомню суть этого эксперимента, после чего расскажу о его новейших постановках. Суть этих повторных экспериментов – наблюдать проявление квантовой вероятности не только в случаях с элементарными частицами, но и с атомами, неорганическими молекулами, крупными органическими молекулами и… так далее. Так нащупывается граница между микромиром и макромиром, то есть, областью доминирования квантовой физики и областью доминирования классической физики.

Эксперимент с двумя щелями

В начале XIX века в научном сообществе, представители которого мыслили в духе детерминизма классической физики, всерьез встал вопрос о том, что представляет собой свет: частицы или волны. Ньютон считал, что свет состоит из мельчайших частиц, «корпускул», что и позволяет объяснить его преломление. С другой стороны, теория Гука-Гюйгенса приводит к выводу, что свет проявляет волновые свойства. Ключевым экспериментом, призванным конкретизировать природу света, стал опыт с двумя щелями, поставленный Томасом Юнгом в 1801 году. Именно Томас Юнг, опираясь на феномен интерференции волн, окончательно сформулировал волновую теорию света, которую проиллюстрировал при помощи своего знаменитого эксперимента:

Свет последовательно пропускается через два барьера, в первом из которых прорезана одна щель, а во втором — две. Если бы свет состоял из частиц-корпускул, то на экране, расположенном за вторым барьером, образовывалось бы две освещенные полосы, по одной напротив каждой из щелей. На самом же деле на экране образуется интерференционный узор, свидетельствующий, что свет распространяется по принципу волны. В 1818 году на основании этих данных Французская Академия выступила с вопросом о том, сможет ли кто-нибудь непротиворечиво объяснить природу света. В результате опытов Жака Френеля и Симеона Дени Пуассона на оставшуюся часть XIX века установилось представление о волновой природе света, которое было вновь оспорено только в 1900 году, когда Планк предложил вышеупомянутую концепцию «кванта». Промежуточным итогом, позволившим вписать физические свойства света в квантовую механику, стала теория корпускулярно-волнового дуализма, сформулированная Луи де Бройлем в 1924 году. Согласно этой теории, свет одновременно проявляет свойства волны и потока частиц.

На фоне такого развития событий в 1927 году Клинтон Дэвиссон и Лестер Джермер повторили эксперимент с двумя щелями на электронах, чтобы показать их дифракцию. Длина волны электрона зависит от энергии частицы, и оказалось, что электрон с энергией 100 эВ (электрон-вольт) имеет длину волны 0,1 нм, что весьма сопоставимо с расстоянием между атомами в кристаллической решетке. Поскольку к тому времени уже удалось получить дифракцию рентгеновских лучей в кристаллической решетке, дифракция электронов также дала ожидаемый результат: два пучка электронов, пропускаемых через две щели, оставляли на экране такие следы, которые должны оставаться от двух волн.

Именно тогда в полной мере началась эпоха квантовых парадоксов, на протяжении которой довелось узнать, что на микроуровне мир устроен существенно иначе, нежели на макроуровне, устроен абсурдно и контринтуитивно. Так, был обнаружен квантовый туннельный эффект, при котором квантовая частица с некоторой вероятностью может преодолеть барьер, непроницаемый для классической частицы. Была выявлена зависимость результата опыта от акта измерения, наиболее ярко представленная в виде мысленного эксперимента под названием «кот Шрёдингера» (а также его усложненного варианта под названием «друг Вигнера»):

Не вдаваясь в подробное описание этих экспериментов, отмечу: характер течения квантовых экспериментов ключевым образом зависит от присутствия или отсутствия наблюдателя. Так, в вышеупомянутой постановке двухщелевого эксперимента с электронами интерференционная картина сохраняется, только когда за ходом эксперимента никто не смотрит. Если эксперимент пронаблюдать, то происходит коллапс волновой функции частицы, и поток электронов разделяется надвое. Электроны начинают вести себя как корпускулы и оставлять на экране не интерференционный узор, а две полосы напротив двух щелей. Данное явление называется «декогеренцией». По какой-то причине поток частиц теряет квантовую согласованность и перестает вести себя как единая волна.

При этом в 1949 году советским ученым Биберману, Сушкину и Фабриканту удалось продемонстрировать, что дифракционные свойства присущи не только потоку электронов, но и отдельному электрону, проходящему через детектор. Буквально в процессе подготовки этой публикации, 20 августа 2021 года, появилась новость об экспериментальном подтверждении корпускулярно-волнового дуализма у одиночного фотона. Дифракцию одиночного фотона выполнила команда во главе с Тай Хён Юн из Южнокорейского института фундаментальных наук. Таким образом, квантовой механике подчиняются мельчайшие частицы наблюдаемого мира… а вот каковы самые крупные объекты, которые также ей подчиняются?

Щель расширяется

В начале XXI была поставлена целая череда экспериментов, демонстрирующих, что двухщелевой эксперимент можно проводить не только с элементарными частицами, но и с атомами, молекулами, крупными молекулами, огромными молекулами и, возможно, даже с вирусами.

Подобные эксперименты гораздо сложнее экспериментов над электронами, как с физической, так и с технологической точки зрения. Создать пучок электронов и пропускать их через две щели можно при помощи электронных пушек, расположенных в вакуумированной камере. С молекулами, особенно крупными, приходится учитывать гораздо больше факторов: вес, форму, ориентацию молекул, а также силу химических связей между атомами в них. Для максимального упрощения этих факторов в одном из первых опытов, призванных исследовать квантовые эффекты на примере больших молекул, использовались фуллерены.

У меня в блоге я уже упоминал новейшие исследования, связанные с фуллеренами; напомню, что фуллерены – это крупные неорганические молекулы, состоящие из атомов углерода. Фуллерен C₆₀ напоминает по форме футбольный мяч, а фуллерен C₇₀ – мяч для регби. В описываемом опыте, поставленном в 1999 году, фуллерены доводили до газообразного состояния, нагревая в керамической печи до температуры 900 K, а затем с силой выдувая через щель в ее корпусе. Действительно, в таком опыте фуллерены демонстрируют интерференционный паттерн, характерный для двухщелевого эксперимента:

В данном случае фуллерены проходили через детектор со скоростью около 200 м/c.

В 2019 году в Венском университете группа под руководством Армина Шайеги успешно провела двухщелевой опыт с молекулой грамицидина, состоящей из 15 аминокислот. Длина волны в таком эксперименте тем меньше, чем больше размер молекулы, поэтому детектор должен быть особенно чувствительным. Кроме того, приходится иметь дело с хрупкостью органических молекул, о которой я писал выше. Для проведения опыта Шайеги с коллегами покрыли тонким слоем грамицидина край вращающегося угольного колесика. Затем этот край бомбардировали лазерными импульсами длительностью по несколько фемтосекунд каждый, отщепляя таким образом молекулы грамицидина и по возможности не повреждая их. После этого отдельные молекулы грамицидина подхватывались струей аргона, гнавшей их в детектор со скоростью 600 м/с. Действительно, в данном эксперименте грамицидин продемонстрировал длину волны в 350 фемтометров.

В сентябре 2019 году там же, в Венском университете, был поставлен еще более амбициозный опыт под руководством Маркуса Арндта. В ходе этого опыта удалось наблюдать волновые квантовые свойства у молекулы размером 2000 атомов, формула которой C₇₀₇H₂₆₀F₉₀₈N₁₆S₅₃Zn₄.

Эти молекулы направляли в детектор, пропуская их через пятиметровую вакуумную трубку. Чтобы они случайно ни с чем не провзаимодействовали, для движения молекул выделили узкий «коридор», а саму трубку защитили от малейших колебаний при помощи системы пружин и амортизаторов. Такая молекула настолько огромна по сравнению с фуллереном и даже с элементарной частицей, что напрашиваются теории, предполагающие, что граница между микро- и макромиром вообще отсутствует, и макроскопические объекты также могут находиться в квантовой суперпозиции, правда, в течение исчезающе малых промежутков времени. В статье об этом эксперименте упоминается теория непрерывной спонтанной локализации (CSL), в соответствии с которой в уравнение Шрёдингера вводится стохастический нелинейный член, фактически разрушающий макроскопические суперпозиции с течением времени.

Вирус Шрёдингера

Итак, переходим к самому интересному. Квантовые эффекты в живой природе объективно реальны, например, именно на них основан фотосинтез. Но можно ли поместить живое существо в квантовую суперпозицию, то есть, провести его одновременно через две щели или воспроизвести эксперимент с котом Шрёдингера, но с участием вируса?

В 2009 году группа О. Ромеро-Изарта из Инсбрукского университета предложила осуществить оптическую левитацию вируса, так, чтобы вирус парил в вакуумной полости, а затем добиться запутанности вируса с квантовым состоянием микроскопического объекта, например, фотона.

Источник

Отголоски прошлого: опыт Юнга в основе нового метода рентгеновской спектроскопии

В 1803 году некий джентльмен опубликовал труд, в котором описывал эксперимент, доказывающий волновую теорию света. Этим джентльменом был Томас Юнг, а его опыт носил название «эксперимент с двумя щелями». Прошло уже более двух веков, но опыт Юнга не был забыт и даже стал фундаментом нового метода рентгеновской спектроскопии, который позволяет более детально изучить физические свойства твердого тела. Итак, почему опыт Юнга считается одним из основополагающих в физике, как его применили современные ученые и что у них из этого получилось мы узнаем из доклада исследовательской группы. Поехали.

Как уже было сказано, в далеком 1803 году Томас Юнг опубликовал описание своего необычного эксперимента. И поскольку «кто не знает прошлого, не имеет будущего», мы коротенько этот опыт с вами рассмотрим.

Томас Юнг

Итак, для проведения опыта было необходимо всего три вещи: свет, пластина с двумя вертикальными прорезями и проекционный экран. При этом световое излучение было монохроматическим, то есть обладало минимальным частотным разбросом. Свет направляется на пластину со щелями, ширина которых должна быть максимально приближена к длине волны излучения. А проекционный экран необходим для наблюдения за результатом.

И тут возникает столкновение двух теорий света — корпускулярной и волновой.

Первая предполагает, что свет состоит из частиц. А вторая — что это волна. Опираясь на каждую из этих теорий мы должны получить разный результат в опыте Юнга.

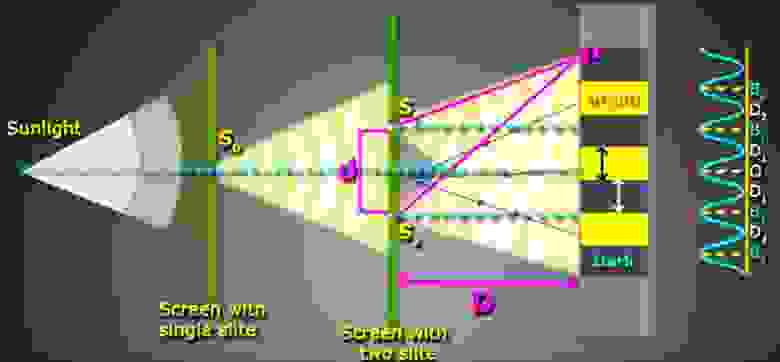
Схематическое изображение опыта Юнга.

Во-первых, источники света (в опыте их два) должны быть когерентными, то есть согласованными. Создать два согласованных световых излучения проблематично, мягко говоря. Посему используется один луч света, который разделяется на два за счет той самой ширмы с прорезями. Так мы имитируем когерентность за счет вторичных волн первичного светового излучения.

Во-вторых, важную роль играет ширина прорезей, так как при ее увеличении будет расти освещенность экрана, то есть сложнее будет различить максимумы и минимумы интерференционной картины. Посему ширина должна быть максимально приближена к длине волны излучения.

И в-третьих, расстояние между прорезями влияет на частоту следования интерференционных полос.

В итоге Томас Юнг не только предоставил доказательства интерференции света, но и породил еще больше споров между сторонниками двух теорий, корпускулярной и волновой.

На самом же деле опыт Юнга никого особо не ссорил (я надеюсь, ибо ученые тоже могут быть драчунами), а скорее подтолкнул к еще более глубокому изучению света, его особенностей и способов его пояснения.

С ростом интереса к квантовой физике опыт Юнга получил еще одну теорию в свою копилку — квантовую. И тут нам фантазия не сильно поможет, поскольку крайне сложно представить себе шарик для страйкбола, способный одновременно быть и частицей, и волной, и разделяться, и соединяться, и черт знает что еще делать. Суть такова — ученые решили провести эксперимент Юнга с электроном, использовав его вместо света.

Ученые «выстреливали» по одному электрону, чтобы у них не было возможности взаимодействовать друг с другом. На пути у них была такая же ширма с двумя прорезями, как и в классическом опыте Юнга, а потом экран для визуализации результатов.

По логике, одиночные электроны, попавшие в прорези, должны сформировать на экране две области попадания, то есть как в корпускулярной теории. Однако мы знаем, что квантовая теория и классическая логика частенько расходятся. Результатом опыта с электронами было множество областей попадания, то есть как в волновой теории. Другими словами, электрон является и частицей, и волной (волна де Бройля, если точнее) одновременно. Таким образом электрон находится в состоянии квантовой суперпозиции, то есть обладает сразу несколькими состояниями, которые невозможно реализовать одновременно с точки зрения классической физики. Да уж, порой кажется, что классическая и квантовая физики это Людвиг ван Бетховен и Оззи Осборн — оба крутые, но во многом очень разные.

Томас Юнг видимо и представить не мог как далеко зайдет его опыт, и как много нового он может рассказать. А сейчас мы рассмотрим уже деяния наших современников, решивших применить опыт Томаса Юнга для реализации нового типа рентгеновской спектроскопии.

Ярким примером принадлежности чего-то и к частицам, и к волнам в квантовой механике является неупругое рассеяние рентгеновского излучения (RIXS). С точки зрения частиц в RIXS рентгеновский фотон выталкивает электрон из ядра атома в валентную оболочку. В этот момент образуется высоковозбужденное атомное состояние, в котором имеется очень локализованная «пустота» размером в несколько пикометров. Такое промежуточное состояние очень быстро распадается, чему соответствует тот факт, что пустота заполняется валентным электроном при переизлучении фотона. Конечное же возбужденное состояние может соответствовать орбитальному, магнитному или межзонному возбуждению.

Исследователи же фокусируются на изучении рентгеновских волн, распространяющихся через вышеупомянутое локализованное промежуточное состояние, а после образующих интерференцию.

Ученые переносят нас немного в прошлое, точнее в 90-ые годы. По их словам уже тогда стало очевидно — даже если в RIXS рассеяние неупругое, а дыра в ядре атома (лучше назвать это термином «вакансия») очень локальна, то все равно амплитуды ее образования и аннигиляции должны быть когерентно суммированы при задействовании идентичных ионов, участвующих в делокализации финального состояния возбуждения. Вследствие всего этого возможна интерференция.

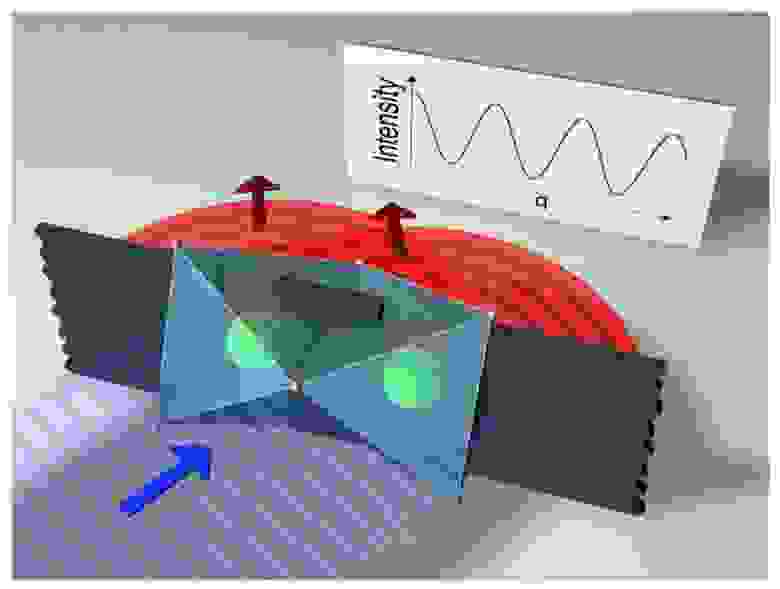
Изображение №1

И вот уже в 1994 году было предположено проявление интерференции для RIXS в двухатомных молекулах, что соответствует опыту Юнга. Это возможно за счет того, что промежуточное состояние RIXS содержит единственную вакансию ядра, которая может быть на любом из двух атомов в молекуле (изображение №1). В конечном состоянии электрон находится на возбужденной молекулярной орбитали, которая делокализована по двум атомам. Рентгеновское же излучение создает интерференцию в виде синусоидального интерференционного колебания на графике.

В качестве основного подопытного был выбран Ba₃CeIr₂O₉ (BCIO) — изолятор, который является кристаллическим твердым телом с квазимолекулярной электронной структурой (2А). Такие характеристики позволяют значительно четче рассмотреть интерференцию, являющуюся ярким признаком симметрии низкоэнергетических электронных возбуждений.

Итак, для начала ученые вырастили индивидуальные кристаллы BCIO. Каждый из Ir 4+ ионов внутри структурных димеров показал 5d 5 конфигурацию с одной вакансией в t_2g оболочке.

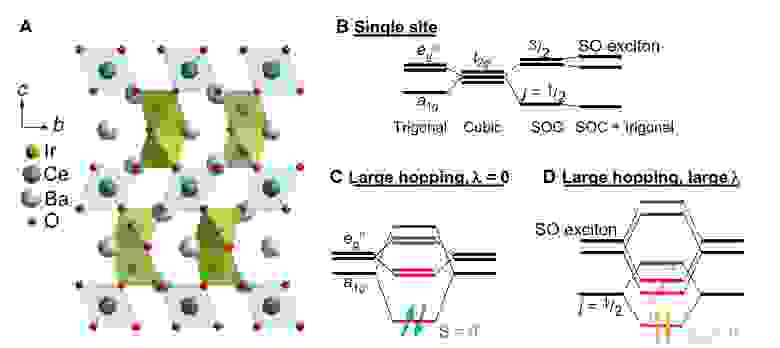
Изображение №2

В случае сильного спин-орбитального взаимодействия связывающие/антисвязывающие состояния могут формироваться из спин-орбитального-запутанного j = 1/2 состояния (2D). Однако сильное Ir-Ir взаимодействие может погасить j = 1/2 моменты. В таком случае t_2g орбитали становятся куда более подходящей основой для формирования связывающих/антисвязывающих состояний (2С).

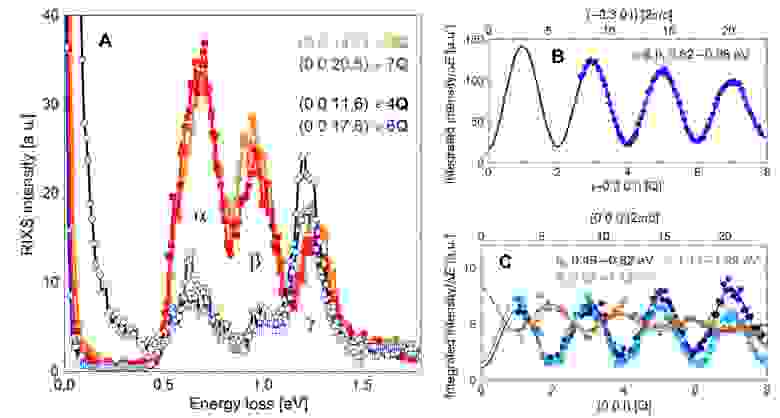
Изображение №3

На изображении 3А мы можем увидеть результаты RIXS образца Ba₃CeIr₂O₉ при фиксированном излучении, настроенном на L3 край Ir (2p→5d), что резонансно усиливает неупругое рассеяние от возбуждений внутри t_2g. 5d t_2g — e δ _g расщепление выше 3 эВ, при этом наблюдаемые функции (a, B и ℽ на графике) находятся в диапазоне 0.5 … 1.5 эВ. Таким образом их можно отнести к внутре-t_2g возбуждениям. Также стоит отметить, что на графике нет характерных для индивидуальных j = 1/2 моментов особенностей, а пик спин-орбитального возбуждения достигает максимума в 1.5 λ.

Исследователи отмечают еще одно важное наблюдение: интегральная интенсивность функций демонстрирует ярко выраженные особенности интерференции двух лучей, другими словами четкое синусоидальное колебание как функции q_c (3B). Таким образом мы получили опыт Юнга, только в данном случае вместо расстояния между прорезями мы имеем расстояние между ионами (Ir-Ir).

Данное исследование — одно из самых сложных из тех, что я встречал, посему настоятельно рекомендую ознакомиться с докладом ученых и дополнительными материалами к нему, если вас интересуют детали, нюансы и подробности сего труда.

Ученые считают, что самой важной особенностью RIXS интерферометрии является возможность определять симметрию низкоэнергетических возбуждений, что помогает отличить два разных варианта орбиталей, описанных на изображениях 2С и 2D.

Конечно, на этом исследование нового метода рентгеновской спектроскопии не завершится, ведь ученые только слегка описали вершину айсберга. Дальнейшие эксперименты с другими типами материалов могут открыть новые пути реализации сей техники. В любом случае совершенствование новейших методик исследования физических свойств даже уже изученных (якобы) объектов это дело благое.

К тому же, данное исследование стало наглядным примером того, что открытия и наблюдения, совершенные несколько веков назад еще способны не только удивлять, но и быть невероятно полезными для создания новых технологий, методик и т.д.

Благодарю за внимание, оставайтесь любопытствующими, несмотря на сложность заинтересовавшего вас материала :), и отличной всем рабочей недели, ребята.

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps до весны бесплатно при оплате на срок от полугода, заказать можно тут.

Источник