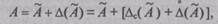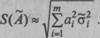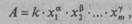В чем заключается особенность расчета погрешностей косвенных измерений

Расчет погрешностей при косвенных измерениях

В большинстве случаев конечной целью лабораторной работы является вычисление искомой величины с помощью некоторой формулы, в которую входят величины, измеряемые прямым путем. Такие измерения называются косвенными. В качестве примера приведем формулу плотности твердого тела цилиндрической формы

, (П.5)

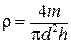
Зависимость (П.5) в общем виде можно представить следующим образом:

, (П.6)

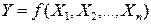
При расчете погрешностей в случае косвенных измерений удобно придерживаться такой последовательности действий:

1) получить средние значения каждой прямо измеряемой величины áX₁ñ, áX₂ñ, …, áX_nñ;

2) получить среднее значение косвенно измеряемой величины áYñ, подставив в формулу (П.6) средние значения прямо измеряемых величин;

4) основываясь на явном виде функции (П.6), получить формулу для расчета абсолютной погрешности косвенно измеряемой величины DY и рассчитать ее;

5) рассчитать относительную погрешность измерения ;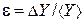

6) записать результат измерения с учетом погрешности.

Ниже без вывода приводится формула, позволяющая получить формулы для расчета абсолютной погрешности, если известен явный вид функции (П.6):

, (П.7)

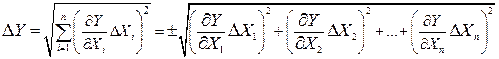
где ¶Y¤¶X₁ и т. д. – частные производные от Y по всем прямо измеряемым величинам X₁, X₂, …, X_n (когда берется частная производная, например по X₁, то все остальные величины X_i в формуле считаются постоянными), DX_i– абсолютные погрешности прямо измеряемых величин, вычисленные согласно (П.3).

Рассчитав DY, находят относительную погрешность .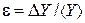

Однако если функция (П.6) является одночленом, то намного легче сначала рассчитать относительную погрешность, а затем уже абсолютную.

Действительно, разделив обе части равенства (П.7) на Y, получим

.

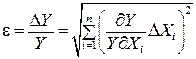
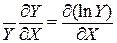
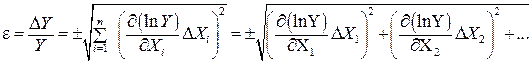
Но так как , то можно записать

. (П.8)

Теперь, зная относительную погрешность, определяют абсолютную .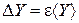

В качестве примера получим формулу для расчета погрешности плотности вещества, определяемой по формуле (П.5). Поскольку (П.5) является одночленом, то, как сказано выше, проще сначала рассчитать относительную погрешность измерения по (П.8). В (П.8) под корнем имеем сумму квадратов частных производных от логарифма измеряемой величины, поэтому сначала найдем натуральный логарифм r:

ln r = ln 4 + ln m – ln p –2 ln d – ln h,

а потом уже воспользуемся формулой (П.8) и получим, что

. (П.9)

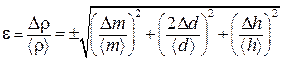
Как видно, в (П.9) используются средние значения прямо измеряемых величин и их абсолютные погрешности, рассчитанные методом прямых измерений по (П.3). Погрешность, вносимую числом p, не учитывают, поскольку ее значение всегда можно взять с точностью, превышающей точность измерения всех других величин. Рассчитав e, находим .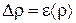

Если косвенные измерения являются независимыми (условия каждого последующего эксперимента отличаются от условий предыдущего), то значения величины Y вычисляются для каждого отдельного эксперимента. Произведя n опытов, получают n значений Y_i. Далее, принимая каждое из значений Y_i (где i – номер опыта) за результат прямого измерения, вычисляют áYñ и DY по формулам (П.1) и (П.2) соответственно.

Окончательный результат как прямых, так и косвенных измерений должен выглядеть так:

, (П.10)

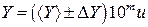
где m – показатель степени, u – единицы измерения величины Y.

Источник

В чем заключается особенность расчета погрешностей косвенных измерений

В лабораторной практике большинство измерений – косвенные и интересующая нас величина является функцией одной или нескольких непосредственно измеряемых величин:

Как следует из теории вероятностей, среднее значение величины определяется подстановкой в формулу (13) средних значений непосредственно измеряемых величин, т.е.

Требуется найти абсолютную и относительную ошибки этой функции, если известны ошибки независимых переменных.

Рассмотрим два крайних случая, когда ошибки являются либо систематическими, либо случайными. Единого мнения относительно вычисления систематической ошибки косвенных измерений нет. Однако, если исходить из определения систематической ошибки как максимально возможной ошибки, то целесообразно находить систематическую ошибку по формулам

Формулой (15) удобно пользоваться в случае, если функция имеет вид суммы или разности аргументов. Выражение (16) применять целесообразно, если функция имеет вид произведения или частного аргументов.

Для нахождения случайной ошибки косвенных измерений следует пользоваться формулами:

В этом случае надежность для доверительного интервала ΔN будет тоже P.

Часто наблюдается случай, когда систематическая ошибка и случайная ошибка близки друг к другу, и они обе в одинаковой степени определяют точность результата. В этом случае общая ошибка ∑ находится как квадратичная сумма случайной Δ и систематической δ ошибок с вероятностью не менее чем P, где P – доверительная вероятность случайной ошибки:

При проведении косвенных измерений в невоспроизводимых условиях функцию находят для каждого отдельного измерения, а доверительный интервал вычисляют для получения значений искомой величины по тому же методу, что и для прямых измерений.

Следует отметить, что в случае функциональной зависимости, выраженной формулой, удобной для логарифмирования, проще сначала определить относительную погрешность, а затем из выражения ΔN = ε ¯ N найти абсолютную погрешность.

Прежде чем приступать к измерениям, всегда нужно подумать о последующих расчетах и выписать формулы, по которым будут рассчитываться погрешности. Эти формулы позволят понять, какие измерения следует производить особенно тщательно, а на какие не нужно тратить больших усилий.

При обработке результатов косвенных измерений предлагается следующий порядок операций:

Приведем примеры расчета ошибки косвенного измерения.

Пример 1.Находится объем цилиндра по формуле

где d – диаметр цилиндра, h – высота цилиндра.

Обе эти величины определяются непосредственно. Пусть измерение этих величин дало следующие результаты:

h = (8.65 ± 0.02) мм, при одинаковой надежности Р = 0.95.

Среднее значение объема, согласно (14) равно

Воспользовавшись выражением (18) имеем:

Систематическая ошибка оказывается сравнимой со случайной, следовательно

Таким образом, результат измерения оказывается

Пример 2. Найти абсолютную и относительную погрешности для следующей функциональной зависимости:

В этом случае удобнее сначала искать относительную погрешность. Тогда

Используя формулу (18), получим

Абсолютную случайную погрешность найдем из выражения

Используя формулу (16) получаем

Абсолютную систематическую ошибку найдем из выражения

Приведем таблицу расчета систематических погрешностей для простейших функций.

Таблица расчета случайных погрешностей для простейших функций.

Источник

В чем заключается особенность расчета погрешностей косвенных измерений

В чем смысл оценки погрешности измерения? В том, что мы задаем границы истинного значения величины, которого мы не знаем, и никогда не сможем узнать, т.к. все измерения всегда делаются с погрешностью. Если, например, значение силы задано вот таким образом:

это означает, что истинное значение лежит между значениями 2,3 Н и 2,5 Н. Эти значения можно назвать «границами» значения этой величины.

При проведении прямых измерений абсолютная погрешность измерения определяется прибором и методом измерения (погрешность отсчета).

Допустим, при смешивании горячей и холодной воды мы имеем следующие результаты измерений:

· температура холодной воды t₁ = (16,0 ± 1,5) °С,

· температура горячей воды t₁ = (66,0 ± 1,5) °С

· температура смеси t = (43,0 ± 1,5) °С,

· масса холодной воды m _х = (80 ± 2) г = (80 ± 2) ∙ 10 –3 кг,

· масса горячей воды m _г = (100 ± 5) г = (100 ± 5) ∙ 10 –3 кг.

Надо рассчитать количества теплоты, полученное холодной водой и отданное горячей при смешивании и сравнить полученные значения в пределах погрешности.

При расчёте количества теплоты, полученного холодной водой, получаем значение:

А для количества теплоты, отданного горячей:

Вычислим верхнюю границу количества теплоты, полученного холодной водой.

Так как количество теплоты определяется умножением, то максимальное количество теплоты получится, если взять для каждого из множителей максимальное значение, то есть верхние границы интервалов значений с погрешностью. А максимальное значение разности получится, если для уменьшаемого взять верхнюю границу значения, а для вычитаемого – нижнюю. Полученное значение будет верхней границей значения количества теплоты:

Аналогично вычисляем нижнюю границу значения количества теплоты:

В полученных границах для Q_пол и лежит искомое значение. Чтобы сравнивать это значение с количеством теплоты, отданным горячей водой методом интервалов, оценим

абсолютную погрешность найденного значения количества теплоты. Из рисунка видно, что

Найденное нами прежде значение для Q_пол близко к значению, найденному как среднее значение границ:

Кроме того, нам все равно придется округлить эти значения в соответствии с вычисленной погрешностью. Поэтому вычислять среднее в дальнейшем не обязательно.

А вот для погрешности найдём следующее значение:

Кстати, если бы мы предварительно округлили бы значения границ, как описывалось, значение погрешности не изменилось бы (проверьте!).

Произведем необходимые округления (до разряда сотен) и запишем значение количества теплоты, полученного холодной водой:

Q_пол = 9100 Дж ± 1200 Дж.

Значит, полученное значение лежит округлённо между 7900 Дж и 10 300 Дж.

Попробуйте рассчитать таким же образом границы значения количества теплоты, отданного горячей водой. Если не получится сделать это самим, посмотрите еще раз, как это делается.

Вычисляем верхнюю границу:

Вычисляем нижнюю границу значения количества теплоты:

Сравнение значений величины с учетом погрешности

11400 Дж. Как сделать вывод о том, равны ли эти значения? Очень просто: надо нанести интервалы значений на числовую ось и посмотреть, перекрываются ли эти интервалы. Из рисунка можно видеть, что эти количества теплоты совпадают в пределах погрешности эксперимента.

Правила округления значения погрешности

Следует пояснить правила округления при записи результатов с погрешностью. Обычно во всех пособиях предлагается в значении абсолютной погрешности оставлять одну значащую цифру. Так, число 0,63 следует округлить до 0,6. Однако надо быть осторожным в случае, если в процессе округления полученная одна значащая цифра является единицей. В этом случае при округлении числа 1,49 до 1 погрешность округления может составить (1,49 – 1)/1 0,49 = 49% от неокруглённого значения, поскольку интервал округления по величине близок к самому значению погрешности. Даже когда единственная значащая цифра после округления 2, погрешность может составить до 25% от самого значения. Поэтому в вузе обычно объясняют студентам, что значение погрешности окончательного результата округляется до одной значащей цифры, но если эта значащая цифра 1 или 2, то до двух. В школьном эксперименте абсолютная погрешность результата около 30% вполне обычное дело, поэтому в значении погрешности рекомендуется оставлять две значащие цифры только в том случае, если первая из них – единица. В значении результата следует оставлять столько десятичных знаков (или разрядов), сколько их в значении погрешности, так как погрешность «поправляет» «неверные» цифры результата.

© Ивашкина Д.А., 2017. Публикация материалов с сайта разрешена только при наличии активной ссылки на главную страницу.

Источник

В чем заключается особенность расчета погрешностей косвенных измерений

Чтобы найти погрешность косвенных измерений, надо воспользоваться формулами, приведенными в таблице. Эти формулы могут быть выведены «методом границ».

Сначала надо вспомнить основные понятия теории погрешности.

Так как мы никогда не знаем точного значения величины А, а лишь определяем из опыта ее приближенное значение, то и величину абсолютной погрешности мы можем определить лишь при­бли­зи­тель­но. Наиболее просто находится максимальная величина абсолютной погрешности, которая и используется нами в лабораторных работах.

Относительная погрешность измерения ε_А равна:

При косвенных измерениях величину погрешности искомой величины вычисляют по формулам:

В случае, когда искомая величина находится по формуле, в которой в основном присутствуют произведение и частное, удобней находить сначала относительную погрешность. Если при этом один из множителей представляет собой сумму или разность, нужно предварительно найти его абсолютную погрешность (сложением абсолютных погрешностей слагаемых), а затем относительную.

Зная относительную погрешность, найти абсолютную погрешность измерений можно так:

«Правило ничтожных погрешностей»

при суммировании погрешностей любым из слагаемых можно пренебречь, если оно не превосходит ⅓ – ⅟ 4 от другого.

Запись результата с указанием погрешности.

Абсолютная погрешность измерений обычно округляется до 1 значащей цифры, а, если эта цифра 1, то до двух.

Результат записывается в виде:

А = А_изм ± ΔА, например: ℓ = (13 ± 2) мм.

Пример оценки погрешностей косвенных измерений № 1

Пример оценки погрешностей косвенных измерений № 2

Задания для самостоятельного решения

Задание 1. Найдите плотность вещества, из которого сделан куб со стороной 7,00 ± 0,15 см, если его масса 847 ± 2 г. Что это за вещество?

Задание 2. Найдите удельную теплоту сгорания топлива, 2,10 ± 0,15 г которого хватило, чтобы нагреть 400 ± 10 мл воды на 35°С ± 2°С. Что это за топливо?

© Ивашкина Д.А., 2017. Публикация материалов с сайта разрешена только при наличии активной ссылки на главную страницу.

Источник

Косвенные измерения

Методика обработки результатов косвенных измерений изложена в документе МИ 2083—90 «ГСОЕИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей». В нем рассмот­рены случаи линейной и нелинейной функции (2.49) при отсутствии и наличии статистической связи (корреляции) между погрешностями из­мерений аргументов. Приводится критерий проверки гипотезы об отсут­ствии указанной корреляции.

Оценка результата и погрешностей измерений.Каждый аргумент в выражении (2.49) измеряется с некоторой погрешностью. Поэтому лю­бой из них можно представить в с ледующем виде:

погрешность результата измерения i-го аргумента, а параметры Δ_с1, и Δ˚_i — систематическая и случайная составляющие погрешности Δ_i.

Задача состоит в том, чтобы с помощью функции (2.49) и ее аргумен­тов найти оценку результата А˜ и его погрешности Δ(А˜) в виде, подоб­ном (2.50):

где Δ_С(А˜) и Δ˚(А˜) — систематическая и случайная составляющие погреш­ности Δ(А˜). Для решения задачи подставим аргументы (2.50) в (2.49), что приводит к выражению

Положим, что в этой формуле погрешности Δ_i, аргументов малы по сравнению с оценкой x˜_i аргументов и что в пределах изменения А,

допустима линеаризация функции (2.52). Учитывая это, разложим данную функцию в ряд Тейлора и оставим в нем только члены перво­го порядка:

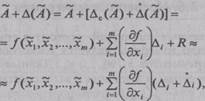остаточный член ряда Тейлора:

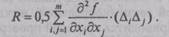Из (2.53) получаем формулу для оценки результата косвенного изме­рения

(2.55)

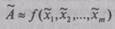
а также выражение для оценки абсолютной систематической погрешно­
сти

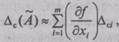в котором частные производные 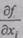называются коэффициентами

влияния i-го аргумента, а слагаемые 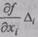— частными погрешностями.

На практике систематические погрешности Δ_i аргументов стремятся устранить, а неисключенные остатки таких погрешностей рассматри­вают как случайные, подчиняющиеся равномерному закону распре­деления. Поэтому выражение для оценки систематической погрешно­сти косвенного измерения, приведенное далее, отличается от соот­ношения (2.56).

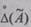
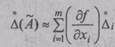Для оценки случайной составляющей погрешности косвенного изме­рения вычитают (2.55) и (2.56) из (2.53). В оставшемся выражении

усредняют квадраты левой и правой части, что позволяет в итоге найти оценку среднеквадратического отклонения S(A) случайной погрешности результата косвенного измерения в зависимости от оценок СКО случайных погрешностей аргументов:

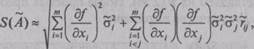где r˜_ij — оценка коэффициента корреляции, определяющего меру ста-

При r˜_ij = 0 оценку СКО S(А˜) вычисляют по формуле

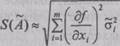Для использования выражений (2.58) и (2.59) требуется вычисление оценок СКО σ˜_i , аргументов функции (2.49) на основе обработки ре­зультатов их многократных наблюдений.

Рассмотрим частные случаи вычисления СКО S(A˜) косвенного изме­рения при отсутствии корреляции между погрешностями измерения ар­гументов.

Пусть функция (2.49) имеет вид суммы

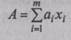Найдя ее частные производные 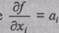и подставив их в (2.59), по-

Предположим, что функция (2.49) имеет вид произведения

(2.64)

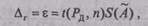
тического отклонения случайной погрешности косвенного измерения (2.59). Коэффициент f_э — эффективное число степеней свободы распре­деления Стьюдента — рекомендуется рассчитывать по приближенной формуле

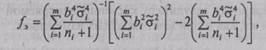Граница θ неисключенных систематических погрешностей результата косвенного измерения вычисляется без учета знака по формуле

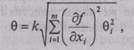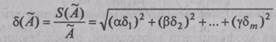где 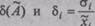— относительные среднеквадратические отклонения

случайных погрешностей результата измерения А˜ и i-го аргумента.

Доверительные границы случайной погрешности и неисключенных систематических погрешностей.При косвенных измерениях, как и при рассмотренных ранее многократных наблюдениях прямых измерений,

здесь θi — заданные границы результатов измерений неисключенных систематических погрешностей аргументов; к — поправочный коэффи­циент, значения которого вычисляются по табл. 2.7 с учетом задаваемой доверительной вероятности Рддля оценки значения θi, а также числа т составляющих θi. Погрешность расчета границы θ по формуле (2.66) не превышает 5%.

Границы погрешности результата косвенного измерения.Суммарные границы ±Δ погрешности результата косвенного измерения вычисляют с учетом границы неисключенных систематических погрешностей 0 (см. формулу (2.66)) и доверительной границы е случайной погрешности (2.64) в зависимости от отношения θ/S(A˜), где S(A˜) — оценка средне-

квадратического отклонения случайной погрешности косвенного измере­ния. Порядок такого учета аналогичен соответствующему учету для однократных прямых измерений и указан в табл. 2.8, где коэффи­циент К зависит от задаваемой доверительной вероятности (Рд = 0,95

или Рд = 0,99) и отношения θ/S(A˜). Значения данного коэффициента при косвенных измерениях выбираются по табл. 2.10.

Таблица 2.10. Зависимости коэффициента К при косвенных измерениях

Результат косвенного измерения и его погрешность должны пред­ставляться в виде формулы

В заключение отметим, что при однократных измерениях аргументов процедура определения результата косвенно измеряемой величины со­храняется такой же, как и при многократных измерениях.

2.7. Метрологические характеристики средств измерений и их нормирование

Каждому виду средств измерений приписываются определенные но­минальные (в данном случае близкие к теоретическим) метрологические характеристики. Реальные же характеристики средств измерений, как правило, не совпадают с номинальными, что и определяет их инстру­ментальные погрешности.

К метрологическим характеристикам средств измерений относятся те, которые оказывают влияние на результаты и погрешности изме­рений. С помощью этих характеристик оценивается погрешность из­мерений, выполняемых используемыми СИ в известных условиях. Для совокупности рабочих средств измерений определенного типа данные о метрологических характеристиках содержатся в нормах, установленных в соответствующих нормативно-технических доку­ментах. Причем отдельный экземпляр СИ должен иметь метроло­гические характеристики, не выходящие за пределы, оговоренные в вышеуказанных документах.

Средства измерений могут применяться в нормальных и рабочих ус­ловиях. Эти условия для конкретных видов СИ установлены в стандар­тах или технических условиях.

Нормальным условиям применения средств измерений должен удовле­творять ряд следующих (основных) требований: температура окружаю­щего воздуха (20±5)°С; относительная влажность (65±15)%; атмосферное давление (100±4) кПа; напряжение питающей сети (220±4) В и (115±2,5)

частота сети (50±1) Гц и (400+12) Гц. Как следует из перечисленных тре­бований, нормальные условия применения СИ характеризуются диапа­зоном значений влияющих на них величин типа климатических факто­ров и параметров электропитания.

Рабочие условия применения СИ определяются диапазоном значений влияющих величин не только климатического характера и параметров электропитания, но и типа механических воздействий. В частности, диа­пазон климатических воздействий делится на ряд групп, охватывающих широкий диапазон изменения окружающей температуры.

Одной из важнейших метрологических характеристик является по­грешность средств измерения, позволяющая оценить инструментальную погрешность (точность) измерения ими физической величины. Причем погрешность средства измерения может быть представлена в форме аб­солютной (Δ), относительной (δ) или приведенной (δ_пр) погрешностей. Указанные погрешности определяются аналогично погрешностям изме­рений, заданным соответственно выражениями (2.1), (2.2) и (2.3). Однако в них вместо результата измерения х должно использоваться показание средства измерения (измерительного прибора) у.

В учебной и технической литературе это показание обозначают ино­гда в виде А, А_п, А_Х, х_п или х_изм.

Как отмечалось в разделе 2.1, погрешность СИ, используемого в нормальных условиях, называется основной, а в условиях, не выхо­дящих за границы рабочих, — дополнительной. Для СИ электриче­ских величин основная и дополнительная погрешности нормируются отдельно. Порядок такого нормирования рассмотрен ниже. Здесь же остановимся на формах представления погрешностей СИ, воспользо­вавшись для их наглядного получения и анализа градуировочной ха­рактеристикой СИ.

Градуировочной характеристикой средства измерения называется за­висимость вида у =f (x) имеющая место между его выходной у и входной х величинами. Пусть функция у_И = f_И (x) — номинальная градуировочная характеристика, которой должно обладать СИ, а у = f(x) — реальная, соответствующая конкретным условиям его использования. Для широ­кого круга средств измерений данные характеристики имеют следую­щую аналитическую форму записи:

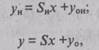где S_Н и S — номинальная и реальная чувствительности СИ, оп­ределяемые выражением (1.4); у_он, у_о, — соответственно выходные ве­личины при отсутствии и наличии так называемой аддитивной (см. ниже) составляющей погрешности.

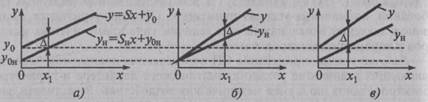Рис. 2.11. Погрешности измерительного прибора: а — абсолютная; 6 — относительная

Соеднеквадратическое отклонение погрешности первого прибора

Некоторые метрологи в области радиотехнических измерений счита­ют энтропийную погрешность более точной и отвечающей современно­му информационному подходу к характеристике процесса измерения физических величин. Информационный подход позволяет с единых по­зиций анализировать измерительные устройства как в статическом, так и в динамическом режимах работы, оптимизировать технические харак­теристики и оценить предельные возможности тех или иных средств из­мерений.

Однако классические методы оценки погрешности измерений также имеют свои преимущества и по-прежнему широко применяются в метро­логии.

Источник