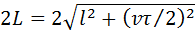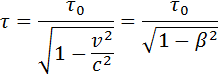В чем заключается относительность промежутка времени между событиями
Относительность длины отрезков и промежутков времени (продолжение)
Релятивистский закон сложения скоростей
3. В теории относительности при переходе от одной системы отсчёта к другой закон преобразования скоростей записывается иначе, чем в классической механике:
где υ — скорость тела в неподвижной системе отсчёта, υ’ — скорость тела в подвижной системе отсчёта, V — скорость подвижной системы отсчёта относительно неподвижной.
При обратном переходе:
Это выражение представляет собой релятивистский закон сложения скоростей.
Относительность промежутков времени
4. В классической механике считается, что время во всех системах отсчёта течёт одинаково. Это означает, что если какой-то физический процесс длится определённое время в неподвижной системе отсчёта, то его длительность в движущейся системе отсчёта будет такой же.
В теории относительности следует ожидать, что длительность физического процесса в разных системах отсчёта будет различной.
Обратимся к мысленному эксперименту. Пусть вдоль платформы движется вагон длиной s = 6 600 000 км со скоростью υ = 240 000 км/с. У задней стенки вагона вспыхивает лампочка (рис. 129). Для наблюдателя, движущегося вместе с вагоном, промежуток времени, через который свет дойдёт до передней стенки вагона, равен
С точки зрения наблюдателя, находящегося на платформе, свет будет «догонять» переднюю стенку вагона, следовательно, он встретится с ней через промежуток времени, равный
Из этого примера видно, что промежуток времени между двумя событиями (вспышка лампочки и встреча луча света с передней стенкой вагона) с точки зрения наблюдателя, находящегося в вагоне, меньше, чем промежуток между этими же событиями с точки зрения наблюдателя, находящегося на платформе.
Таким образом, в теории относительности промежуток времени между одной и той же парой событий различен в разных системах отсчёта.
Из формулы следует, что промежуток времени между двумя событиями имеет наименьшую длительность в той системе отсчёта, в которой оба события произошли в одной и той же точке пространства. Во всех других системах отсчёта он будет иметь тем большую длительность, чем больше скорость движения.
Движущиеся часы по сравнению с неподвижными отстают. Часто говорят, что в движущейся системе отсчёта происходит замедление времени. Точно так же, как относительность длины, замедление времени связано с движением системы отсчёта.
Итак, промежуток времени между двумя событиями — величина относительная, зависящая от скорости движения системы отсчёта. Время, измеренное по часам, движущимся вместе с тем телом, с которым происходят события, называют собственным временем для данного процесса.
В чем заключается относительность промежутка времени между событиями
Популярно об Эйнштейне и СТО
А вот еще один взгляд на теорию относительности: в одном интернет-магазине продаются часы, у которых нет секундной стрелки. Зато с той же скоростью относительно часовой и минутной вращается циферблат. А в названии этих часов присутствует имя знаменитого физика « Эйнштейн».
Относительность промежутков времени состоит в том, что ход часов зависит от движения наблюдателя. Движущиеся часы отстают от неподвижных: если какое-либо явление имеет определенную длительность для движущегося наблюдателя, то оно кажется более продолжительным для неподвижного. Если бы система двигалась со скоростью света, то неподвижному наблюдателю движения в ней казались бы бесконечно замедленными. В этом заключается знаменитый «парадокс часов».
Пример
Если я одновременно (для себя) щелкаю пальцами на раздвинутых руках, то для меня промежуток времени между щелчками равен нулю (предполагается, что я это проверил способом Эйнштейна — встречные световые сигналы вместе пришли в середину расстояния между парами щелкающих пальцев). Но тогда для любого наблюдателя, движущегося «боком» относительно меня, щелчки будут не одновременны. А значит, по его отсчету мое мгновение станет некоей длительностью.
Наоборот, если он щелкает пальцами на раздвинутых руках и с его точки зрения щелчки одновременны, то для меня они окажутся неодновременными. Поэтому его мгновение я воспринимаю как длительность.
Подобно этому, мое «почти мгновение» — очень короткая длительность — для движущегося наблюдателя растягивается. А его «почти мгновение» растягивается для меня. Словом, мое время для него замедляется, его же время замедляется для меня.
Правда, в этих примерах не сразу видно, что во всех системах отсчета сохраняется направление времени — обязательно от прошлого к будущему. Но это легко доказать, вспомнив о запрете сверхсветовых скоростей, что делает невозможным движение во времени вспять.
Еще один пример
Элла и Алла — космонавтки. Они летят на разных ракетах в противоположные стороны и проносятся мимо друг друга. Девушки любят смотреться в зеркальце. Кроме того, обе девушки наделены сверхчеловеческой способностью видеть и обдумывать неуловимо быстрые явления.
Элла сидит в ракете, разглядывает собственное отражение и размышляет о неумолимом беге времени. Там, в зеркале, она видит себя в прошлом. Ведь свет от ее лица сначала дошел до зеркала, потом отразился от него и вернулся обратно. На это путешествие света ушло время. Значит, Элла видит себя не той, какая она есть теперь, а чуть-чуть более молодой. Примерно на трехсотмиллионную долю секунды – т.к. скорость света равна 300 000 км/с, а путь от лица Эллы до зеркала и обратно — примерно 1 метру. «Да, — думает Элла, — даже увидеть себя можно только в прошлом!»
Алла, летящая на встречной ракете, поравнявшись с Эллой, приветствует ее и любопытствует, чем занята подруга. О, она смотрится в зеркало! Однако, Алла, заглянув в зеркало Эллы, приходит к иным заключениям. По оценке Аллы, Элла стареет медленнее, чем по оценке самой Эллы!
В самом деле, пока свет от лица Эллы добрался до зеркала, зеркало относительно Аллы сместилось — ведь ракета движется. На обратном пути света Алла отметила дальнейшее смещение ракеты.
Значит, для Аллы свет шел туда и обратно не по одной прямой линии, а по двум разным, несовпадающим. На пути «Элла — зеркало — Элла» свет шел углом, описал нечто похожее на букву «Д». Поэтому с точки зрения Аллы он прошел больший путь, чем с точки зрения Эллы. И тем больший, чем больше относительная скорость ракет.
Алла — не только космонавт, но и физик. Она знает: по Эйнштейну, скорость света всегда постоянна, в любых системах отсчета одинакова, т.к. не зависит от скорости движения светового источника. Следовательно, и для Аллы и для Эллы скорость света составляет 300 000 км/с. Но если с одной и той же скоростью свет умеет проходить в разных системах отсчета разные пути, вывод отсюда единственный: время в разных системах отсчета течет по-разному. С точки зрения Аллы, свет у Эллы прошел больший путь. Значит, на это и времени ушло больше, иначе скорость света не сохранилась бы неизменной. По измерениям Аллы, время у Эллы течет медленнее, чем по измерениям самой Эллы.
Последний пример
Если астронавт вылетает с Земли со скоростью, отличающейся от скорости света на одну двадцатитысячную, летит по прямой в течение года туда (отсчитанного по его часам и по событиям его жизни), а затем возвращается обратно. По часам астронавта на это путешествие уходит 2 года.
Вернувшись на Землю, он обнаружит (согласно релятивистской формуле замедления времени), что жители Земли состарились на 100 лет (по земным часам), т. е. встретит уже другое поколение.
Формула релятивистского замедления времени:
Источник: из книг Г. Амфилова «Бегство от удивлениний», М. Льоцци «История физики»
Кто первый?
Во время учебы в школе А. Эйнштейн часто задавал себе вопрос «Что мог бы видеть человек, движущийся за световой волной со скоростью света?».
А в работе Гегеля «Диалектика природы» есть цитата: «Свет есть налично сущая чистая сила наполнения пространства, и его бытие является абсолютной скоростью». Оказывается, он предвосхитил А. Эйнштейна.
О нём
Знаменитые уравнения Эйнштейна — основа общей теории относительности — были опубликованы в 1916 году. После этого один из крупнейших современных физиков Дж. Уилер сказал: «В общей теории относительности, пространство «говорит» материи как ей двигаться, а материя «указывает» пространству как ему искривляться.»
Знаменитый физик Нильс Бор в 1961 году говорил: «На каждом этапе Эйнштейн бросал вызов науке, и не будь этих вызовов, развитие квантовой физики затянулось бы надолго».
В чем заключается относительность промежутка времени между событиями
Существование единого мирового времени, не зависящего от системы отсчета, которое принималось как очевидный факт в классической физике, эквивалентно неявному допущению о возможности синхронизации часов с помощью сигнала, распространяющегося с бесконечно большой скоростью.
С релятивистским эффектом замедления времени связан так называемый « парадокс близнецов ». Предполагается, что один из близнецов остается на Земле, а второй отправляется в длительное космическое путешествие с субсветовой скоростью. С точки зрения земного наблюдателя, время в космическом корабле течет медленнее, и когда астронавт возвратится на Землю, он окажется гораздо моложе своего брата-близнеца, оставшегося на Земле. Парадокс заключается в том, что подобное заключение может сделать и второй из близнецов, отправляющийся в космическое путешествие. Для него медленнее течет время на Земле, и он может ожидать, что по возвращению после длительного путешествия на Землю он обнаружит, что его брат-близнец, оставшийся на Земле, гораздо моложе его.
Чтобы разрешить «парадокс близнецов», следует принять во внимание неравноправие систем отсчета, в которых находятся оба брата-близнеца. Первый из них, оставшийся на Земле, все время находится в инерциальной системе отсчета, тогда как система отсчета, связанная с космическим кораблем, принципиально неинерциальная. Космический корабль испытывает ускорения при разгоне во время старта, при изменении направления движения в дальней точке траектории и при торможении перед посадкой на Землю. Поэтому заключение брата-астронавта неверно. СТО предсказывает, что при возвращении на Землю он действительно окажется моложе своего брата, оставшегося на Земле.
В настоящее время уже необходимо принимать во внимание релятивистский эффект замедления хода часов при транспортировке атомных часов на большие расстояния.
Учебник. Относительность промежутков времени
При выполнении любых физических измерений исключительную роль играют пространственно-временные соотношения между событиями. В СТО событие определяется как физическое явление, происходящее в какой-либо точке пространства в некоторый момент времени в избранной системе отсчета. Таким образом, чтобы полностью охарактеризовать событие, требуется не только выяснить его физическое содержание, но и определить его место и время. Для этого необходимо использовать процедуры измерения расстояний и промежутков времени. Эйнштейн показал, что эти процедуры нуждаются в строгом определении.
Для того чтобы в выбранной системе отсчета выполнять измерения промежутка времени между двумя событиями (например, началом и концом какого-либо процесса), происходящими в одной и той же точке пространства, достаточно иметь эталонные часы. Наибольшей точностью в настоящее время обладают часы, основанные на использовании собственных колебаний молекул аммиака (молекулярные часы) или атомов цезия (атомные часы). Измерение промежутка времени опирается на понятие одновременности: длительность какого-либо процесса определяется путем сравнения с промежутком времени, отделяющим показание часов, одновременное с концом процесса, от показания тех же часов, одновременного с началом процесса. Если же оба события происходят в разных точках системы отсчета, то для измерения промежутков времени между ними в этих точках необходимо иметь синхронизованные часы.
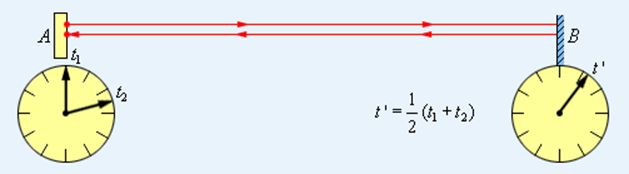
Эйнштейновское определение процедуры синхронизации часов основано на независимости скорости света в пустоте от направления распространения. Пусть из точки A в момент времени t1 по часам A отправляется короткий световой импульс (рис. 4.2.1). Пусть время прихода импульса в B и отражения его назад на часах B есть t’. Наконец, пусть отраженный сигнал возвращается в A в момент t2 по часам A. Тогда по определению часы в A и B идут синхронно, если t’ = (t1 + t2) / 2.
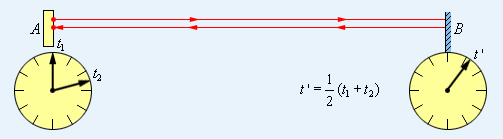
Существование единого мирового времени, не зависящего от системы отсчета, которое принималось как очевидный факт в классической физике, эквивалентно неявному допущению о возможности синхронизации часов с помощью сигнала, распространяющегося с бесконечно большой скоростью.
Итак, в разных точках выбранной системы отсчета можно расположить синхронизованные часы. Теперь можно дать определение понятия одновременности событий, происходящих в пространственно-разобщенных точках: эти события одновременны, если синхронизованные часы показывают одинаковое время.
Рассмотрим теперь вторую инерциальную систему K’, которая движется с некоторой скоростью υ в положительном направлении оси x системы K. В разных точках этой новой системы отсчета также можно расположить часы и синхронизировать их между собой, используя описанную выше процедуру. Теперь интервал времени между двумя событиями можно измерять как по часам в системе K, так и по часам в системе K’. Будут ли эти интервалы одинаковы? Ответ на этот вопрос должен находиться в согласии с постулатами СТО.
Пусть оба события в системе K’ происходят в одной и той же точке и промежуток времени между ними равен τ0 по часам системы K’. Этот промежуток времени называется собственным временем. Каким будет промежуток времени между этими же событиями, если его измерить по часам системы K?
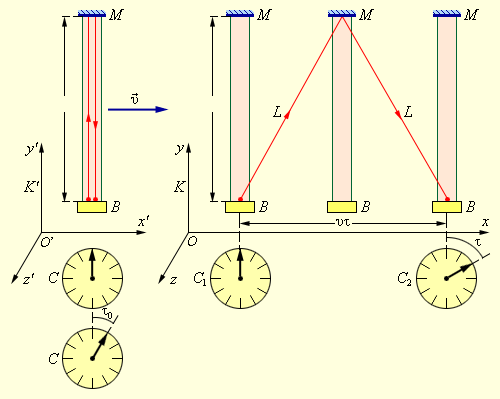
Для ответа на этот вопрос рассмотрим следующий мысленный эксперимент. На одном конце твердого стержня некоторой длины l расположена импульсная лампа B, а на другом конце – отражающее зеркало M. Стержень расположен, неподвижно в системе K’ и ориентирован параллельно оси y’ (рис. 4.2.2). Событие 1 – вспышка лампы, событие 2 – возвращение короткого светового импульса к лампе.
Таким образом, промежуток времени между двумя событиями зависит от системы отсчета, т. е. является относительным. Собственное время τ0 всегда меньше, чем промежуток времени между этими же событиями, измеренный в любой другой системе отсчета. Этот эффект называют релятивистским замедлением времени. Замедление времени является следствием инвариантности скорости света.
С релятивистским эффектом замедления времени связан так называемый «парадокс близнецов». Предполагается, что один из близнецов остается на Земле, а второй отправляется в длительное космическое путешествие с субсветовой скоростью. С точки зрения земного наблюдателя, время в космическом корабле течет медленнее, и когда астронавт возвратится на Землю, он окажется гораздо моложе своего брата-близнеца, оставшегося на Земле. Парадокс заключается в том, что подобное заключение может сделать и второй из близнецов, отправляющийся в космическое путешествие. Для него медленнее течет время на Земле, и он может ожидать, что по возвращению после длительного путешествия на Землю он обнаружит, что его брат-близнец, оставшийся на Земле, гораздо моложе его.
Чтобы разрешить «парадокс близнецов», следует принять во внимание неравноправие систем отсчета, в которых находятся оба брата-близнеца. Первый из них, оставшийся на Земле, все время находится в инерциальной системе отсчета, тогда как система отсчета, связанная с космическим кораблем, принципиально неинерциальная. Космический корабль испытывает ускорения при разгоне во время старта, при изменении направления движения в дальней точке траектории и при торможении перед посадкой на Землю. Поэтому заключение брата-астронавта неверно. СТО предсказывает, что при возвращении на Землю он действительно окажется моложе своего брата, оставшегося на Земле.
В настоящее время уже необходимо принимать во внимание релятивистский эффект замедления хода часов при транспортировке атомных часов на большие расстояния.
Относительность промежутков времени
При выполнении любых физических измерений исключительную роль играют пространственно-временные соотношения между событиями. В СТО событие определяется как физическое явление, происходящее в какой-либо точке пространства в некоторый момент времени в избранной системе отсчета. Таким образом, чтобы полностью охарактеризовать событие, требуется не только выяснить его физическое содержание, но и определить его место и время. Для этого необходимо использовать процедуры измерения расстояний и промежутков времени. Эйнштейн показал, что эти процедуры нуждаются в строгом определении.
Для того чтобы в выбранной системе отсчета выполнять измерения промежутка времени между двумя событиями (например, началом и концом какого-либо процесса), происходящими в одной и той же точке пространства, достаточно иметь эталонные часы. Наибольшей точностью в настоящее время обладают часы, основанные на использовании собственных колебаний молекул аммиака (молекулярные часы) или атомов цезия (атомные часы). Измерение промежутка времени опирается на понятие одновременности: длительность какого-либо процесса определяется путем сравнения с промежутком времени, отделяющим показание часов, одновременное с концом процесса, от показания тех же часов, одновременного с началом процесса. Если же оба события происходят в разных точках системы отсчета, то для измерения промежутков времени между ними в этих точках необходимо иметь синхронизованные часы.
Эйнштейновское определение процедуры синхронизации часов основано на независимости скорости света в пустоте от направления распространения. Пусть из точки A в момент времени t1 по часам A отправляется короткий световой импульс (рис. 4.2.1). Пусть время прихода импульса в B и отражения его назад на часах B есть t’. Наконец, пусть отраженный сигнал возвращается в A в момент t2 по часам A. Тогда по определению часы в A и B идут синхронно, если t’ = (t1 + t2) / 2.
Синхронизация часов в СТО
Существование единого мирового времени, не зависящего от системы отсчета, которое принималось как очевидный факт в классической физике, эквивалентно неявному допущению о возможности синхронизации часов с помощью сигнала, распространяющегося с бесконечно большой скоростью.
Итак, в разных точках выбранной системы отсчета можно расположить синхронизованные часы. Теперь можно дать определение понятия одновременности событий, происходящих в пространственно-разобщенных точках: эти события одновременны, если синхронизованные часы показывают одинаковое время.
Рассмотрим теперь вторую инерциальную систему K’, которая движется с некоторой скоростью υ в положительном направлении оси x системы K. В разных точках этой новой системы отсчета также можно расположить часы и синхронизировать их между собой, используя описанную выше процедуру. Теперь интервал времени между двумя событиями можно измерять как по часам в системе K, так и по часам в системе K’. Будут ли эти интервалы одинаковы? Ответ на этот вопрос должен находиться в согласии с постулатами СТО.
Пусть оба события в системе K’ происходят в одной и той же точке и промежуток времени между ними равен τ0 по часам системы K’. Этот промежуток времени называется собственным временем. Каким будет промежуток времени между этими же событиями, если его измерить по часам системы K?
Для ответа на этот вопрос рассмотрим следующий мысленный эксперимент. На одном конце твердого стержня некоторой длины l расположена импульсная лампа B, а на другом конце – отражающее зеркало M. Стержень расположен, неподвижно в системе K’ и ориентирован параллельно оси y’ (рис. 4.2.2). Событие 1 – вспышка лампы, событие 2 – возвращение короткого светового импульса к лампе.
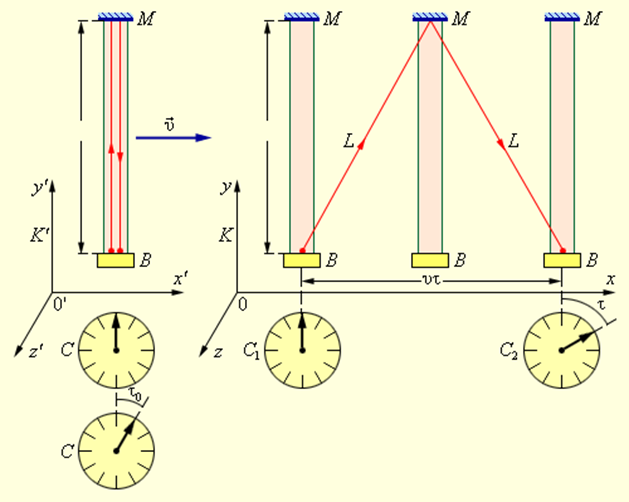
Относительность промежутков времени. Моменты наступлений событий в системе K’ фиксируются по одним и тем же часам C, а в системе K – по двум синхронизованным пространственно-разнесенным часам C1 и C2. Система K’ движется со скоростью υ в положительном направлении оси x системы K
В системе K’ оба рассматриваемых события происходят в одной и той же точке. Промежуток времени между ними (собственное время) равен τ = 2l / c. С точки зрения наблюдателя, находящегося в системе K, световой импульс движется между зеркалами зигзагообразно и проходит путь 2L, равный
где τ – промежуток времени между отправлением светового импульса и его возвращением, измеренный по синхронизованным часам C1 и C2, расположенными в разных точках системы K. Но согласно второму постулату СТО, световой импульс двигался в системе K с той же скоростью c, что и в системе K’. Следовательно, τ = 2L / c.
Из этих соотношений можно найти связь между τ и τ0:
Таким образом, промежуток времени между двумя событиями зависит от системы отсчета, т. е. является относительным. Собственное время τ0 всегда меньше, чем промежуток времени между этими же событиями, измеренный в любой другой системе отсчета. Этот эффект называют релятивистским замедлением времени. Замедление времени является следствием инвариантности скорости света.
Эффект замедления времени является взаимным, в согласии с постулатом о равноправии инерциальных систем K и K’: для любого наблюдателя в K или K’ медленнее идут часы, связанные с системой, движущейся по отношению к наблюдателю. Этот вывод СТО находит непосредственное опытное подтверждение. Например, при исследовании космических лучей в их составе обнаружены μ-мезоны – элементарные частицы с массой, примерно в 200 раз превышающей массу электрона. Эти частицы нестабильны, их среднее собственное время жизни равно τ0 = 2,2·10 –6 с. Но в космических лучах μ-мезоны движутся со скоростью, близкой к скорости света. Без учета релятивистского эффекта замедления времени они в среднем пролетали бы в атмосфере путь, равный cτ0 ≈ 660 м. На самом деле, как показывает опыт, мезоны за время жизни успевают пролетать без распада гораздо большие расстояния. Согласно СТО, среднее время жизни мезонов по часам земного наблюдателя равно 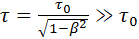
С релятивистским эффектом замедления времени связан так называемый «парадокс близнецов». Предполагается, что один из близнецов остается на Земле, а второй отправляется в длительное космическое путешествие с субсветовой скоростью. С точки зрения земного наблюдателя, время в космическом корабле течет медленнее, и когда астронавт возвратится на Землю, он окажется гораздо моложе своего брата-близнеца, оставшегося на Земле. Парадокс заключается в том, что подобное заключение может сделать и второй из близнецов, отправляющийся в космическое путешествие. Для него медленнее течет время на Земле, и он может ожидать, что по возвращению после длительного путешествия на Землю он обнаружит, что его брат-близнец, оставшийся на Земле, гораздо моложе его.
Чтобы разрешить «парадокс близнецов», следует принять во внимание неравноправие систем отсчета, в которых находятся оба брата-близнеца. Первый из них, оставшийся на Земле, все время находится в инерциальной системе отсчета, тогда как система отсчета, связанная с космическим кораблем, принципиально неинерциальная. Космический корабль испытывает ускорения при разгоне во время старта, при изменении направления движения в дальней точке траектории и при торможении перед посадкой на Землю. Поэтому заключение брата-астронавта неверно. СТО предсказывает, что при возвращении на Землю он действительно окажется моложе своего брата, оставшегося на Земле.
Эффекты замедления времени пренебрежимо малы, если скорость космического корабля гораздо меньше скорости света c. Тем не менее, удалось получить прямое подтверждение этого эффекта в экспериментах с макроскопическими часами. Наиболее точные часы – атомные работающие на пучке атомов цезия-133. Эти часы «тикают» 9192631770 раз в секунду. Американские физики в 1971 году провели сравнение двух таких часов, причем одни из них находились в полете вокруг Земли на обычном реактивном лайнере, а другие оставались на Земле в военно-морской обсерватории США. В соответствии с предсказаниями СТО, путешествующие на лайнерах часы должны были отстать от находящихся на Земле часов на (184 ± 23)·10 –9 с. Наблюдаемое отставание составило (203 ± 10)·10 –9 с, т. е. в пределах ошибок измерений. Через несколько лет эксперимент был повторен и дал результат, согласующийся со СТО с точностью 1 %.
В настоящее время уже необходимо принимать во внимание релятивистский эффект замедления хода часов при транспортировке атомных часов на большие расстояния.