В чем заключается парадокс эйлера даламбера
Парадокс Даламбера
Парадокс Даламбера — утверждение в гидродинамике идеальной жидкости, согласно которому при непрерывном стационарном обтекании тела безграничным поступательным потоком невязкой жидкости, при условии выравнивания параметров далеко впереди и позади тела, сила сопротивления равна нулю.
Содержание
Варианты названия парадокса
Историческая справка
Различные варианты парадокса Даламбера
В силу принципа относительности Галилея можно говорить и о парадоксе Даламбера в случае поступательного движения тела с постоянной скоростью в безграничном объеме идеальной жидкости, который покоится на бесконечности.
Кроме этого парадокс Даламбера справедлив при обтекании тела потоком, заключенным в бесконечный цилиндрический канал.
Особенности формулировки парадокса Даламбера
Важно отметить, что в формулировке парадокса говорится только об отсутствии составляющей силы, действующей на тело, которая параллельна потоку на бесконечности (об отсутствии силы сопротивления). Составляющая силы, которая перпендикулярна потоку (подъемная сила), может быть отлична от нуля даже при выполнении всех условий парадокса (так, например, обстоит дело для двумерных задач: подъемная сила вычисляется по известной формуле Жуковского).
Обратим внимание на то, что момент сил, действующих на тело со стороны потока, может быть, вообще говоря, отличен от нуля. Так, при безотрывном обтекании наклонённой к потоку пластинки даже при нулевой циркуляции скорости (и, следовательно, при нулевой подъемной силе) возникает момент сил, стремящийся повернуть пластинку поперёк потока.
При наличии объемных сил (например, силы тяжести) со стороны жидкости на тело может действовать сила Архимеда, однако ее нельзя считать составляющей силы сопротивления, ибо она не обращается в нуль в покоящейся жидкости.
Случаи нарушения парадокса Даламбера
Как это хорошо известно, при обтекании тела реальным потоком жидкости всегда имеется ненулевая сила сопротивления, наличие которой объясняется нарушением тех или иных условий, входящих в формулировку парадокса Даламбера. В частности,
Если создать условия, в которых обтекание тела будет достаточно близко к условиям в формулировке парадокса Даламбера, например придать телу обтекаемую (каплеобразную или эллипсоидальную) форму, то возможно добиться существенного — в десятки и сотни раз — снижения сопротивления по сравнению с плохообтекаемыми (например, в форме куба) телами с тем же миделевым сечением.
Учебники
Журнал «Квант»
Общие
Бетяев С. Гидродинамические парадоксы //Квант. — 1998. — № 1. — С. 5-9.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Обстоятельства, с которыми мы сталкиваемся, кажутся на первый взгляд совершенно парадоксальными с чисто математической точки зрения и предусмотреть их можно только из физических соображений. Ж.Адамар
Содержание
Парадоксом называют неожиданное суждение, резко противоречащее общепринятому. Практическое значение парадоксов — двигателей прогресса — состоит в том, что они заставляют по-новому посмотреть на основы старой теории и построить другую, более совершенную теорию, а зачастую и новую науку. Специальная теория относительности — это разрешение парадокса о конечности скорости передачи информации, квантовая механика — разрешение парадокса о прерывистости сигнала в микромире. Парадоксы «породили» физику элементарных частиц и современную космологию, стимулировали развитие современной математики.
Самые фундаментальные парадоксы, стоящие на развилке наук, формулируют и разрешают гении. Это подметил еще А.С.Пушкин:
«О, сколько нам открытий чудных
Готовят просвещенья дух
И опыт, сын ошибок трудных,
И гений, парадоксов друг,
И случай, бог изобретатель.»
В науке различают опытное суждение, установленное с помощью эксперимента, и теоретическое суждение, основанное на математическом моделировании явления. Поэтому можно говорить о трех типах научных парадоксов.
Первый из них — противоречие между общепринятым теоретическим суждением и вновь полученным теоретическим суждением. Такой самый простой тип парадокса («теория — теория») возникает в результате улучшения математической модели или усовершенствования метода расчета.
Второй тип парадокса — противоречие между общепринятым опытным суждением и вновь полученным опытным суждением («опыт-опыт») — заслуживает более подробного рассмотрения, чем мы и займемся, отложив на время в сторону определение и анализ парадоксов третьего типа.
Парадоксы симметрии
Всегда ли симметрия причин приводит к симметрии следствия? В микромире — не всегда (об этом можно прочитать, например, в книге Р.Фейнмана «Характер физических законов» — Библиотечка «Квант», вып. 62). И в гидродинамике тоже не всегда. Картина обтекания симметричного тела, помещенного в симметричный поток, зачастую оказывается несимметричной. В этом заключена сущность парадокса симметрии.
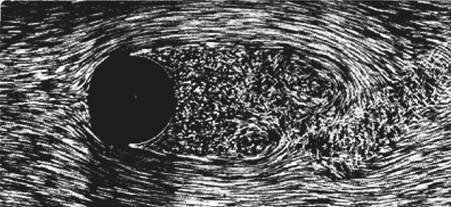
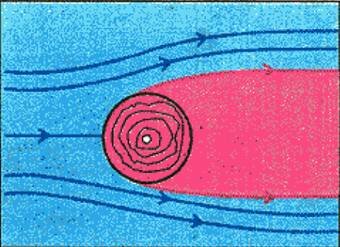
На рисунке 1 показано симметричное обтекание кругового цилиндра потоком воды. Траектории частиц жидкости сделаны видимыми (визуализированными) с помощью алюминиевого порошка; вода движется слева направо. Верхняя и нижняя половинки симметричны — одна из них является зеркальным отражением другой. Более того, почти симметрично обтекание передней и задней частей цилиндра. Рисунок 2 иллюстрирует обтекание того же цилиндра в других условиях. Симметрия «верх—низ» сохранена, но симметрия левой и правой частей нарушена — за цилиндром образовались две замкнутые зоны с противоположно направленными вращениями частиц жидкости. Наконец, на рисунке 3 представлена картина обтекания цилиндра в условиях, когда нарушена симметрия обоих типов. Обтекание нестационарно, изменяется с течением времени (визуализация осуществлялась с помощью воздушных пузырьков в воде).
Почему течение теряет симметрию? Исчерпывающе ответить на этот вопрос в настоящее время нельзя. Поэтому подменим его другим, более простым. Например, чем отличаются условия обтекания цилиндров в трех рассмотренных случаях? Оказывается — разным отношением действующих на частицу сил: силы лобового сопротивления и вязкой силы. Это отношение характеризуется так называемым числом Рейнольдса Re (безразмерным параметром). При малых числах Re силы вязкости значительны, тело движется, как дробинка в меде (рисунку 1 соответствует Re = 1,5, рисунку 2 — Re = 26). При больших числах Re силы вязкости малы, поток становится неустойчивым и даже хаотическим (рисунку 3 соответствует Re = 2000).
Смена симметрии, их внезапное разрушение — фундаментальный закон современной гидродинамики. В реальных условиях абсолютная симметрия невозможна, в потоке всегда есть асимметрия. Поэтому если считать, что симметричные причины влекут за собой симметричные последствия, то почти симметричные причины могут приводить к совсем несимметричным последствиям. В этом заключается одно из объяснений парадокса симметрии.
Парадокс Эйфеля
Представим аэродинамическую силу лобового сопротивления в виде
F \sim \rho u^2_ <\infty>l^2\), где ρ — плотность, u∞ — скорость невозмущенного набегающего потока, а l — характерный размер тела, легко получить из соображений размерностей (проверьте!). А коэффициенты \(
\frac<\pi><4>\), Cx записаны для удобства. Безразмерный коэффициент сопротивления Cx можно определить из экспериментов. Он обычно убывает с ростом числа Re, т.е. с уменьшением сил вязкого трения.
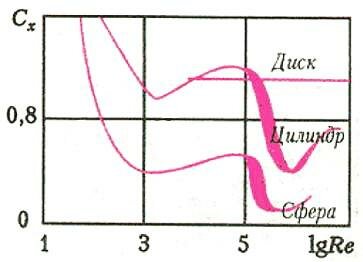
Парадокс Эйфеля обнаружен не только при обтекании сферы, но и при обтекании других тел. На рисунке 4 представлена полученная экспериментально зависимость Cx(Re) для сферы, кругового цилиндра и диска, при этом тела имеют один и тот же диаметр l. На участке резкого изменения Cx для сферы и цилиндра наблюдается разброс экспериментальных данных, показанный на рисунке «дорожкой». Коэффициент сопротивления диска практически постоянен — для тел с острыми кромками парадокс Эйфеля не справедлив. Объяснение парадокса заключается в том, что вблизи критического значения числа Рейнольдса происходит переход от плавного, стационарного течения, называемого ламинарным, к нестационарному, хаотическому движению, называемому турбулентным. Малое изменение Re приводит к большой перестройке течения.
Такая ситуация, когда малое изменение какого-либо параметра приводит к коренному изменению течения, типична для гидродинамики. Именно она объясняет многочисленные парадоксы расходимости опытных данных — проведенные при, казалось бы, одних и тех же условиях измерения оказываются совершенно различными. Поэтому при моделировании обтекания тел в аэрогидродинамических трубах следует учитывать влияние стенок трубы, поддерживающих модель устройств, неоднородностей в набегающем потоке, физико-химических свойств поверхности модели (шероховатость, смачиваемость, теплопроводность). Сделать это чрезвычайно трудно, если не сказать — невозможно.
Парадокс Дюбуа
Исследования Дюбуа показали, что сила сопротивления, действующая со стороны потока на покоящееся в трубе тело, в определенном диапазоне чисел Re меньше, чем сила сопротивления, действующая на движущееся с той же скоростью тело в покоящейся воде. В соответствии с принципом относительности, результат не должен зависеть от того, движется ли тело в покоящейся жидкости или жидкость обтекает покоящееся тело. Как же объяснить парадокс Дюбуа?
Конечно, влиянием тех факторов, о которых уже упоминалось. Поток в опытном бассейне или в аэродинамической трубе более неравномерен, чем в «спокойном» море или атмосфере, поэтому переход к турбулентному режиму здесь наступает раньше, т.е. при докритических значениях Re, след за телом сужается, сопротивление падает. Парадокс Дюбуа не утратил своей актуальности и в наше время. Различие между результатами трубного эксперимента и натурного, проводимого в условиях реального полета, остается для гидродинамиков проблемой номер один.
Если вы видели когда-нибудь вертолет на стоянке, то должны были заметить, как низко, почти на метр, свисают его лопасти. Лишь в полете они распрямляются. Точно так же крыло самолета под действием аэродинамических сил изменяет в полете свою форму. Изменяет незначительно, а результаты скрупулезных (и дорогих!) экспериментальных исследований оказываются совсем неверными. Таким образом, для объяснения несоответствия между результатами трубного и натурного экспериментов приходится учитывать, кроме всего прочего, упругие свойства конструкций, подверженных действию гидродинамических сил.
Подошло время сказать о парадоксах третьего типа. Кроме парадоксов типа «теория—теория» и «опыт—опыт», существуют еще парадоксы типа «теория-опыт» (или «опыт—теория»). Для них характерно резкое противоречие между теоретическими результатами и тем, что мы называем опытом, интуицией или просто «здравым смыслом».
Самый известный из парадоксов типа «теория-опыт» — это парадокс Эйлера — Даламбера. В 1742 году петербургский академик Л.Эйлер рассчитал сопротивление цилиндра, движущегося в жидкости, лишенной трения, и получил удивительный результат — сила сопротивления оказалась равной нулю! Спустя семь лет выдающийся французский механик Ж.Даламбер с помощью некоторых ухищрений рассчитал обтекание произвольного тела конечного объема и получил все тот же ошеломляющий результат — нулевое сопротивление.
Такой вывод резко отличался от «здравого смысла». Даламбер, как и каждый из нас, из личного опыта знал, что для поддержания движения к телу необходимо приложить силу тяги, преодолевающую силу сопротивления (именно поэтому летательные аппараты, корабли и подводные лодки снабжены двигателями). Даламбер не смог объяснить полученный результат и с горечью заметил, что нулевое сопротивление — «единственный парадокс, разрешение которого я оставляю геометрам будущих времен».
Прямо скажем: геометрам (гидродинамикам и математикам) достался в наследство крепкий орешек. Прежде чем его раскалывать, выясним геометрический смысл парадокса. Течение, исследованное Эйлером и Даламбером, симметрично, т.е. правая половина течения совпадает с левой (аналогично рисунку 1). Следовательно, совпадающая с направлением невозмущенного потока составляющая импульса (количества движения) струйки, обтекающей тело, постоянна: в некотором сечении слева вдали от тела она такая же, как в некотором сечении справа вдали от тела. В соответствии с законом сохранения импульса, на струйку, как и на помещенное в нее тело, не действует сила сопротивления. Математическая модель, использованная Эйлером и Даламбером, оказалась переупрощенной. Реальные течения несимметричны (подобно тем, которые изображены на рисунках 2 и 3).
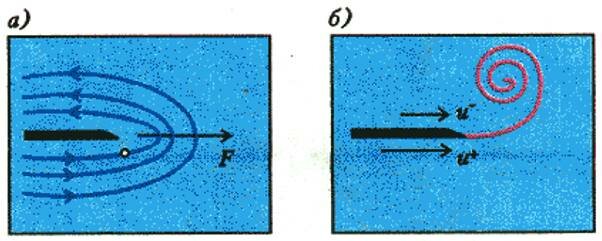
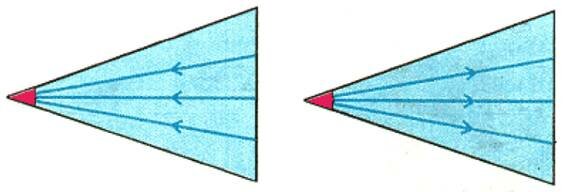
Кроме парадокса Эйлера — Даламбера, известно много парадоксов «переупрощения математической модели». Так, безотрывное обтекание острой кромки пластины (рис. 6,а) приводит к «парадоксу бесконечности» — скорость жидкости при подходе к кромке неограниченно растет. Более того, для разворота потока на 180° требуется так называемая центростремительная сила. В силу третьего закона Ньютона на пластину будет действовать такая же по величине сила (ее называют подсасывающей). К чему она приложена? К кромке пластины, т.е. к точке! Реальное обтекание кромки — отрывное, от нее отходит линия разрыва касательной составляющей скорости (окрашенная на рисунке 6,б в красный цвет), скорость на кромке конечна.
Корректность математической модели
Разработка непарадоксальной математической модели, адекватно описывающей реальный процесс, — очень сложное дело. В большинстве случаев об этом приходится только мечтать, поэтому известный математик Д.Биркгоф в шутку предложил разделить гидродинамиков на экспериментаторов, которые наблюдают то, что нельзя описать, и теоретиков, которые описывают то, что нельзя наблюдать.
Пришла пора сделать выводы. Во избежание парадоксов математическая модель течения не должна быть переупрощенной — следует учитывать тот фактор, пренебрежение которым приводит к парадоксу. С точки зрения физика, такое требование естественно. Однако математик подходит к этому вопросу строже (такова его профессия). С точки зрения математика, постановка задачи должна быть корректной. Корректность включает три требования к математической модели: существование решения, его единственность и устойчивость.
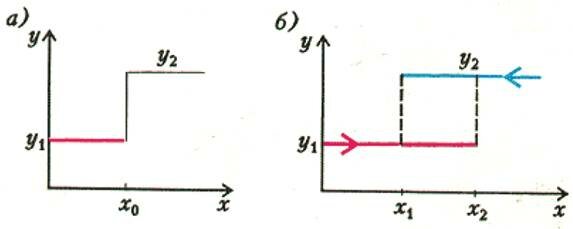
Ну а как поступить, если имеется несколько решений? Допустим, при решении квадратного уравнения вы получили два корня. Какой из них выбрать? Давайте переберем все возможные случаи, обратившись к опыту. Если в опыте не реализуется ни один из возможных корней, то это означает, что математическая модель — квадратное уравнение — несправедлива. Если в опыте реализуется лишь один из полученных корней, то он оказывается устойчивым по отношению к малым внешним возмущениям, а другой корень — неустойчивым. Наконец, имеется третья возможность — когда могут реализоваться оба решения. Если при значении параметра (х = x0) происходит смена одного решения (у = y1) на другое (у = y2), то говорят о бифуркации решения (рис. 8,а). Если в некотором диапазоне значений параметра (x1 x2, обратный ход). В этом случае выбор решения зависит от предыстории процесса. (Гистерезисные режимы обтекания крыла наблюдаются, например, вблизи значения угла атаки α, соответствующего максимальному значению коэффициента подъемной силы Cy)
С парадоксами неединственности ученые столкнулись еще на заре развития авиации. В 1910 году на авиационном салоне под Парижем молодой ученый из Румынии А.Коанда поднял в воздух сконструированный им самолет, который смело можно назвать прототипом современных реактивных летательных аппаратов. Из сопел, расположенных по бокам фюзеляжа, вырывались огненные струи. После успешного полета отделавшийся ушибами изобретатель принимал восторженные поздравления. «Молодой человек! Вы опередили эпоху на 30, а то и на все 50 лет!» — сказал ему Эйфель. Но триумфатор думал о другом — о странном поведении огненной струи во время разбега самолета. Струя вместо того чтобы отражаться от специально установленных металлических щитков, защищающих фанерный фюзеляж от воспламенения, прижималась к ним, разворачиваясь в обратную сторону.
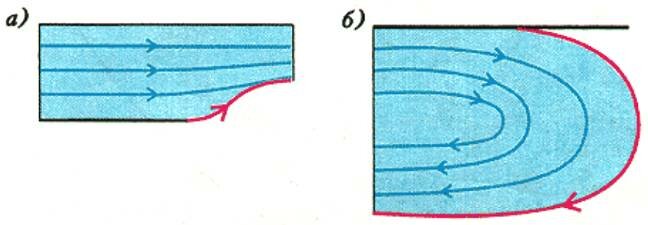
С эффектом Коанда мы встречаемся каждый день, досадуя, что струя, вытекающая из носика чайника, вдруг прилипает к его поверхности и льется мимо чашки. Такой поворот струи и прилипание к твердой поверхности гидродинамики в шутку называют еще «эффектом чайника». На рисунке 9, а показана схема истечения струи из канала без поворота, а на рисунке 9,б — с поворотом. Получено два решения. Но разгадан ли парадокс Коанда? К сожалению, нет — неизвестно, при каких условиях реализуется тот или иной режим.
Мы не обсудили еще один критерий корректности математической модели — устойчивость решения. Случайные, неустойчивые по отношению к малым возмущениям процессы нельзя исследовать с помощью классического аппарата математики. Определить отдельную беспорядочную траекторию невозможно, как невозможно предсказать, будет ли дождь через месяц. В лучшем случае можно рассчитывать на получение некоторых общих выводов. Очень хорошо об этом сказал русский поэт и философ В.С.Соловьев:
«Природа с красоты своей
Покрова снять не позволяет,
И ты машинами не вынудишь у ней,
Чего твой дух не угадает».
Парадокс неустойчивости заключается в том, что обтекание тела при стационарных внешних условиях зависит от времени. Пример нестационарного течения демонстрирует, например, рисунок 3. Обтекание становится нестационарным, когда число Рейнольдса превышает некоторое критическое значение. Доподлинно известно, что нестационарность вызвана неустойчивым характером отрыва потока от тела, но до окончательного разрешения парадокса нестационарности еще далеко.
Д’Аламбера — Эйлера парадокс
Полезное
Смотреть что такое «Д’Аламбера — Эйлера парадокс» в других словарях:
Д’АЛАМБЕРА — ЭЙЛЕРА ПАРАДОКС — положение гидродинамики, согласно к рому при равномерном и прямолинейном движении тела внутри безграничной жидкости, лишённой вязкости, вихреобразований и поверхностей разрыва скоростей, результирующая сила сопротивления жидкости движению тела… … Физическая энциклопедия
ДАламбераЭйлера парадокс — (по имени Ж. Л. ДАламбера и Л. Эйлера) равенство нулю сопротивления аэродинамического для тела конечного размера, обтекаемого безвихревым, установившимся, не отрывающимся от тела потоком идеальной жидкости при отсутствии в нём… … Энциклопедия «Авиация»
ДАламбераЭйлера парадокс — (по имени Ж. Л. ДАламбера и Л. Эйлера) равенство нулю сопротивления аэродинамического для тела конечного размера, обтекаемого безвихревым, установившимся, не отрывающимся от тела потоком идеальной жидкости при отсутствии в нём… … Энциклопедия «Авиация»
Эйлера-Д′аламбера парадокс — см. Д′Аламбера Эйлера парадокс. Авиация: Энциклопедия. М.: Большая Российская Энциклопедия. Главный редактор Г.П. Свищев. 1994 … Энциклопедия техники
Парадокс Даламбера — утверждение в гидродинамике идеальной жидкости, согласно которому при непрерывном стационарном обтекании тела безграничным поступательным потоком невязкой жидкости, при условии выравнивания параметров далеко впереди и позади тела, сила… … Википедия
ЭйлерадАламбера парадокс — ЭйлерадАламбера парадокс то же, что ДАламбераЭйлера парадокс … Энциклопедия «Авиация»
ЭйлерадАламбера парадокс — ЭйлерадАламбера парадокс то же, что ДАламбераЭйлера парадокс … Энциклопедия «Авиация»
Аэродинамика — (от греческого аer воздух и dynamis сила) 1) раздел механики сплошных сред, в котором изучаются закономерности движения жидкостей и газов (преимущественно воздуха), а также механическое и тепловое взаимодействие между жидкостью или газом и… … Энциклопедия техники
«Обстоятельства, с которыми мы сталкиваемся, кажутся на первый взгляд совершенно парадоксальными с чисто математической точки зрения, и предусмотреть их можно только из физических соображений».
«Природа с красоты своей
Покрова снять не позволяет,
И ты машинами не вынудишь у ней,
Чего твой дух не угадает».
В 1742 году петербуржский академик Л. Эйлер рассчитал сопротивление цилиндра, равномерно движущегося в жидкости, лишенной трения, и получил удивительный результат — сила сопротивления оказалась равной нулю! Спустя семь лет выдающийся французский механик Ж. Даламбер с помощью некоторых ухищрений рассчитал обтекание произвольного тела конечного объема и получил все тот же ошеломляющий результат — нулевое сопротивление. Такой вывод резко отличался от «здравого смысла». Даламбер не смог объяснить полученный результат и с горечью заметил, что нулевое сопротивление — «единственный парадокс, разрешение которого я оставляю геометрам будущих времен».
Для нас этот парадокс интересен тем, что он фактически положен в основу Хиггсовского механизма образования массы материи, который в корне противоречит нашему механизму явления врождённой инерции. Механизм образования массы по Хиггсу заключается в том, что инертность частицы может проявиться при её неравномерном (ускоренном) движении только сквозь какую-то среду. Такой средой, по мнению Хиггса, может быть физический вакуум, носителями которого являются, так называемые бозоны Хиггса. Если тело движется с постоянной скоростью сквозь жидкость без вязкости и без турбулентности, то жидкость будет обтекать тело, не оказывая ему в целом никакого сопротивления (в гидродинамике это называется парадоксом Даламбера). Однако при попытке изменить скорость тела у него обнаружится некоторая дополнительная инертность, называемая присоединенной массой.
В нашей модели явления инерции, кроме врождённого свойства материи преобразования напряжение-движение, являющегося основой явления инерции (см. главу 1.2.1.), б О льшую количественную часть инерционного сопротивления так же обеспечивает мировая материальная среда, правда состоящая не из бозонов Хиггса, а из элементарных носителей среды амеров. Однако механизм образования инерции, обеспечиваемый средой, в нашей версии принципиально отличается от образования массы по Хиггсу.
Как показано в главе (1.2.1.), все физические тела, которые на микроуровне практически более чем на 90% состоят из пустоты, почти не взаимодействуют со средой при равномерном движении, т.к. амеры преимущественно свободно пролетают между невозмущёнными при равномерном движении материальными структурами вещества. И лишь при деформации тел их внутреннее пространство наполняется свободными амерами вещества, которые и образуют парус взаимодействия, улавливающий ветер взаимодействия, состоящий из амеров среды, что и вызывает эффект вторичного инерционного сопротивления ускоренному движению. При этом первичным остаётся врождённое свойство материи преобразование напряжение-движение, без которого никакого эффекта инерционности не может быть в принципе (см. гл. 1.2.1).
Во-первых, такая «инерционность» не зависит от свойств самого тела, которые якобы и при равномерном движении, и при ускоренном движении остаются абсолютно одинаковыми, т.е. исключается физическая деформация тела, которая происходит при любом взаимодействии, а, следовательно, и само взаимодействие. Это фактически инерция без деформации, а, следовательно, и без взаимодействия. В такой модели инерционность тела фактически является свойством изменяющегося относительного движения материи, а вовсе не самой материи!Ё? Непонятно так же, как в условиях полного отсутствия вязкости к телу может присоединиться так называемая присоединённая масса среды, ведь ей в этом случае просто нечем зацепиться за тело.
Во-вторых, модель инерции, основанной только на внешнем сдерживании движения материи средой в отсутствие собственной инерции материи, т.е. в отсутствие свойства материи (среды) преобразование напряжение-движение, не имеет физического смысла, т.к. она не объясняет физическую природу собственно самой инерции. Не имея собственного свойства инерции, материя среды не может передать его телу, т.к. передать можно только то, что есть у самого передающего объекта. Ведь если массу образуют бозоны Хиггса, то для образования массы самих бозонов Хиггса нужны бозоны Хиггса второго порядка и так до бесконечности. Причём, если в этом бесконечном ряду хотя бы в одном из его бесконечных порядков не будет собственной массы, то её не будет и у всего ряда. Это означает, что даже вся вселенная не сможет оказать никакого инерционного сопротивления даже самой маленькой из всех известных и даже ещё неизвестных частиц материи.
Кроме того, парадокс Эйлера-Даламбера не имеет опытного подтверждения в реальной действительности не только потому, что в природе нет ничего идеального, в том числе и идеальной невязкой жидкости, а главным образом потому, что парадокс Эйлера-Даламбера — это чисто математический парадокс, не имеющий никакого отношения к действительности реального взаимодействия материи. Парадокс Эйлера-Даламбера получен при помощи, оторванных от физики и потому абсолютно бессмысленных чисто математических манипуляций с теоремой Бернулли.
Вот официальное математическое доказательство парадокса Эйлера-Даламбера:
получим требуемое равенство:
F – сила давления потока жидкости, которая по всем существующим законам физики должна действовать на тело (А).
В нашей версии физическая сущность свойства материи преобразование напряжение–движение, т.е. инерции, отражена не в парадоксе Даламбера–Эйлера, а в самом законе Бернулли для несжимаемой жидкости ( m * V 2 / 2 + Р * V = const ). Объём неизменного массового элемента жидкости в заданном неразрывном потоке жидкости так же остаётся неизменным. Поэтому когда поток жидкости встречает на своём пути сужение трубопровода, давление перед сужением локально увеличивается. При этом потенциальная энергия (Р * V ), образованная силой давления на неизменный объём неизменного массового элемента жидкости перед сужением и за его кормой так же увеличивается. Эта потенциальная энергия под действием избыточного давления набегающего потока постепенно реализуется в движение массового элемента жидкости внутри сужения, что сопровождается увеличением его кинетической энергии ( m * V 2 / 2). Потенциальная энергия за его кормой внутри сужения соответственно уменьшается на такую же величину, что равносильно уменьшению давления неразрывного потока внутри сужения. В расширении всё повторяется с точностью до наоборот.
Таким образом, в отсутствие каких–либо дополнительных внешних сил для потока в целом, кроме тех, что затрачиваются на преодоление общего сопротивления (трения) трубы, суммарная энергия каждого массового элемента потока в полном соответствии с законом сохранения энергии остаётся неизменной. Однако сохранение энергии обеспечивается компенсацией внешней силой общего сопротивления потоку со стороны трубы.
Как показано в главе (1.2.1.) уравнение Бернулли является идеалистической математической записью принципа действия врождённого свойства материи преобразование напряжение–движение. Однако даже из идеализированного варианта уравнения Бернулли следует, что напряжение образуется из движения по мере его расходования и наоборот, т.е. существует отрицательная обратная связь этого преобразования, что и обеспечивает его инерционность в виде конечного ускорения инерции. Следовательно, преобразование напряжение–движение осуществляется не мгновенно, а с определённым ускорением, что и воспринимается нами, как инерция.
Как только из напряжения образуется движение, само напряжение уменьшается строго на величину энергии, которая и затрачена на это движение. При этом прирост нового движения соответственно замедляется, т.к. он происходит за счёт уже несколько уменьшенного напряжения, и наоборот, что и есть инерция. То есть само понятие инерция предполагает постепенное преобразование напряжение–движение с определённым ускорением, обусловленным отрицательной обратной связью процесса преобразования напряжение–движение, а вовсе не мгновенное преобразование. Именно наличие конечного ускорения, вместо мгновенного разгона или торможения и обуславливает эффект инерции.
Поэтому сам по себе парадокс Эйлера–Даламбера не может лежать в основе явления инерции, как считает Хиггс. Парадокс Эйлера–Даламбера основан на выравнивании давлений и скоростей жидкости в отдалённых от тела сечениях. При этом голая математика, для которой исходным начальным условием является сам факт выравнивания давлений на расстоянии от тела, не учитывает физические процессы, происходящие непосредственно вблизи тела (массового элемента). Это всё равно, что судить об одном явлении природы совершенно по другому явлению, происходящему совсем в другой точке пространства.
И ещё один важный момент.
Отсутствие вязкости означает не только её отсутствие между элементами самой жидкости, но отсутствие трения между жидкостью и телом. Но трение есть не что иное, как взаимодействие между поверхностями, а, значит, и между телами. То есть условие отсутствия вязкости исключает часть общего взаимодействия, в том числе и соответствующую часть его математического описания. Естественно, что такое описание будет парадоксальным. Поэтому совершенно непонятно, что так упорно ищут шарлатаны от физики – сторонники Стандартной модели на БАК–е в Церне? Ведь их модель построена на неправильном математическом описании реальной действительности! Ё!