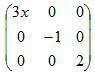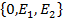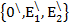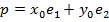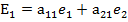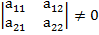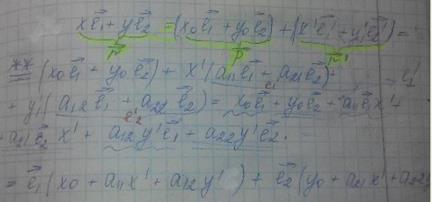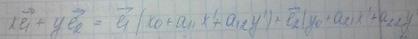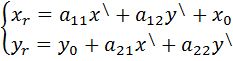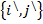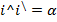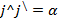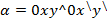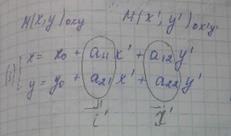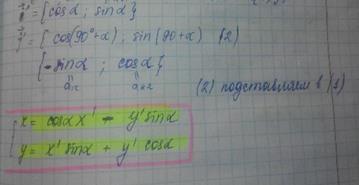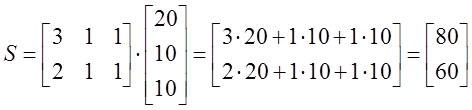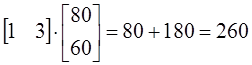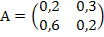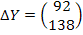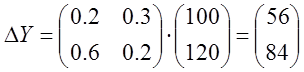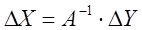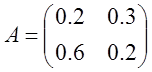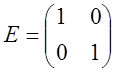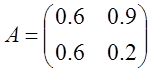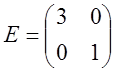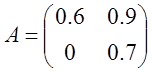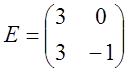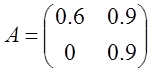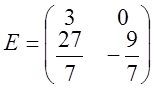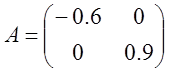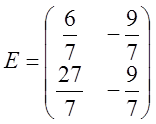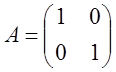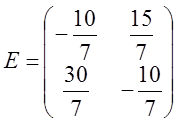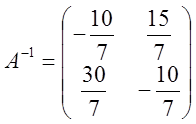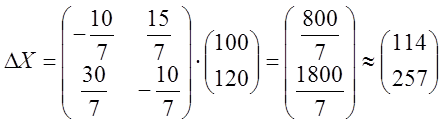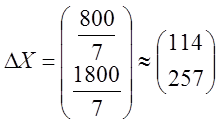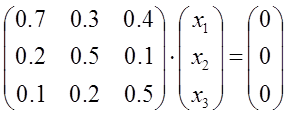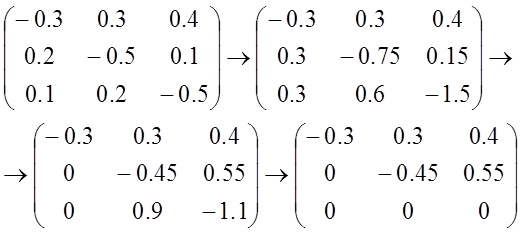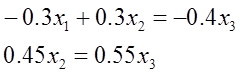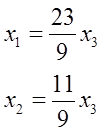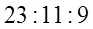В чем заключается правило многоугольника сложения
Операции над векторами и их свойства: сложение и умножение
Прежде чем приступить к тематике статьи, напомним основные понятия.
Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.
Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.
Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.
Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.
Сложение двух векторов
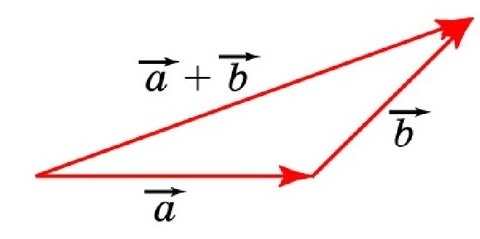
Геометрически сложение векторов выглядит так:
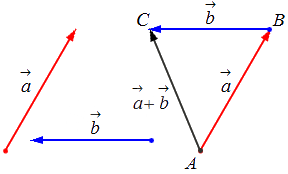
— для неколлинеарных векторов:
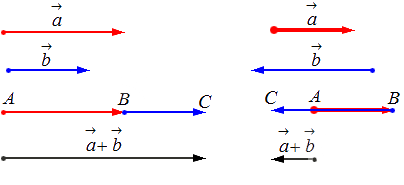
— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:
Сложение нескольких векторов
Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.
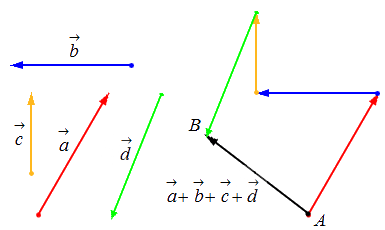
Геометрически оно выглядит следующим образом:
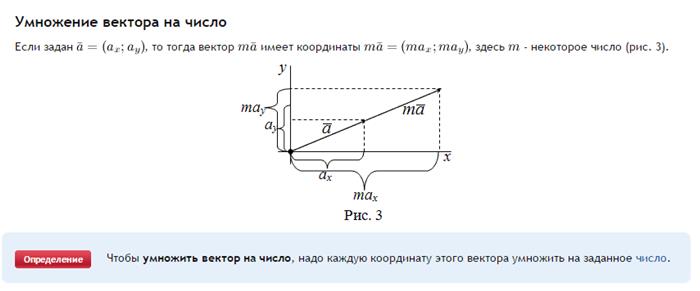
Умножение вектора на число
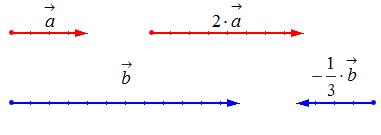
Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:
Свойства операций над векторами
Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.
Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.
Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.
Сложение векторов в геометрии
Основные законы сложения векторов в геометрии
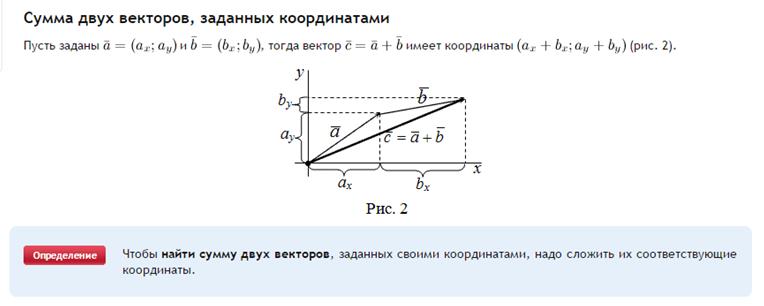
На плоскости найти сумму векторов можно, воспользовавшись формулой:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если ситуация переходит в пространственное измерение, то достаточно всего лишь а тот же пример добавить новую координату:
Основные законы:
Помимо покоординатного сложения направленных отрезков, существуют геометрические нормы, которые позволяют узнать их сумму. Наиболее широко используемых методов в системе три: правило треугольника, параллелограмма и многоугольника.
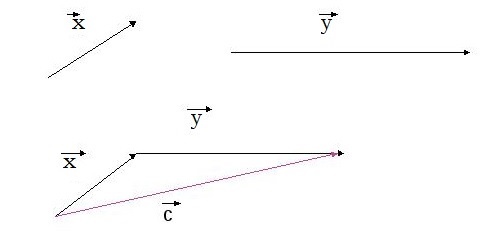
Как происходит сложение по правилу треугольника
Чтобы узнать сумму векторов x и y, необходимо из произвольной точки отложить первый из них, а затем из его конца уже отложить второй. Следующий шаг — построить направленный отрезок, который соединит начало \vec x с концом \vec y. Образовавшаяся сторона треугольника и будет результатом сложения двух векторов. Теорема считается доказанной.
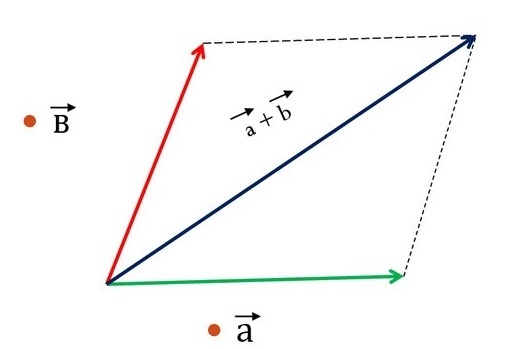
Сложение по правилу параллелограмма
Найти сумму векторов можно без построения треугольника. Для этого от начала первого вектора нужно отложить второй вектор. Дополним получившийся чертеж до параллелограмма. Две его стороны у нас уже имеются. Выстроить оставшиеся поможет способ параллельного переноса. Диагональ готовой фигуры, которая исходит из начальной точки векторов, считается их суммой. Теорема доказана.
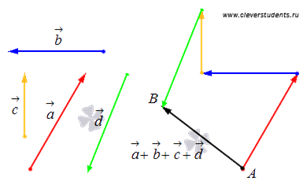
Как и когда применяется правило многоугольника
Данный способ потребуется для того, чтобы сложить более двух векторов.
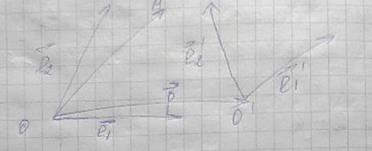
Принцип действий в данном случае похож на последовательность шагов, как в случае с треугольником. Из произвольной точки провести первый вектор. Из его конца — второй, из второго — третий и так далее. Затем окончание последнего вектора соединить с началом первого — это будет результат сложения всех векторов. Доказательство теоремы выполнено.
Задачи с примерами решения
Задача 1
Решение
Задача 2
С помощью правила треугольника постройте сумму заданных векторов a и b.
Решение 1
Решение 2
Одна цель достигнута разными способами, что наглядно демонстрирует действие переместительного закона.
К коллинеарным векторам это построение неприменимо.
Основываясь на рассмотренной операции сложения двух векторов, мы можем сложить три вектора и более. В этом случае складываются первые два вектора, к полученному результату прибавляется третий вектор, к получившемуся прибавляется четвертый и так далее.
Сложение нескольких векторов на плоскости таким способом называется правилом многоугольника. Приведем иллюстрацию правила многоугольника.
1.3. Умножение вектора на число k соответствует растяжению вектора в k раз при k > 1 или сжатию в 1/k раз при 0
Числа aij, входящие в состав данной матрицы, называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j — номер столбца.
Строка матрицы называется нулевой, если все ее элементы равны нулю.
Если хотя бы один из элементов строки матрицы не равен нулю, то строка называется ненулевой.
Столбец матрицы называется нулевым, если все его элементы равны нулю.
Если хотя бы один из элементов столбца матрицы не равен нулю, то столбец называется ненулевым.
2. Квадратной матрицейназывается матрица, у которой количество строк равно количеству столбцов (размера n×n), число n называется порядком матрицы.
 | -7 |  | — квадратная матрица размера 3×3 |
| -1 |
Нулевой матрицейназывается матрица, все элементы которой равны нулю, т.е. aij = 0, ∀i, j.
 |  | — нулевая матрица |
Вектор-строкой называется матрица, состоящая из одной строки.
 | -5 |  | — вектор-строка |
Вектор-столбцом называется матрица, состоящая из одного столбца.
 |  | — вектор-столбец |
| -7 |
Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.
 |  | — не диагональные элементы равны нулю |
Единичной матрицей называется диагональная матрица, диагональные элементы которой равны 1.
| E = |  |  | — диагональные элементы равны 1 |
Верхней треугольной матрицей называется матрица, все элементы которой ниже главной диагонали равны нулю.
 | -6 |  |
Нижней треугольной матрицей называется матрица, все элементы которой выше главной диагонали равны нулю.
 |  |
| -2 |
Ступенчатой матрицей называется матрица, удовлетворяющая следующим условиям:
· если матрица содержит нулевую строку, то все строки, расположенные под нею, также нулевые;
· если первый ненулевой элемент некоторой строки расположен в столбце с номером i, и следующая строка не нулевая, то первый ненулевой элемент следующей строки должен находиться в столбце с номером большим, чем i.
 |  |
| -3 |
 |  |
7. Преобразования координат на плоскости. Ориентация плоскости.
R=
Рассмотрим еще один R ̸̸ на той же плоскости R ̸̸ =
Рассмотрим вектор х на той же самой плоскости, возникает вопрос: как будут связаны между собой координаты этого вектора в 1 и во 2 базисе.
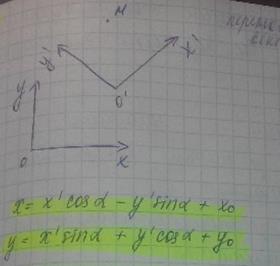
Полученные формулы будут называться формулами преобразования координат на плоскости.
Рассмотрим на плоскости точку М относительно старой системы координат, то это будут два числа (х,у)R М=(х,у)R
Связь между координатами R1=xe1+ye2 и 
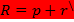
Если мы рассмотрим вектора нового базиса относительно старого базиса, то


А т.к. базисные вектора линейно независимые, значит каждый из них ненулевой вектор и они неколлинеарные, т.е. а11 и а21 ≠ 0 или 
То что вектора не коллинеарные означает
Эти условия записываются в виде палочек а внутри типо таблица, это похоже на матрицу:
Таким образом мы получим
Эти формулы называются формулами преобразования координат на плоскости
Для прямоугольной декартовой системы координат эти формулы примут вид:
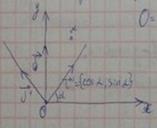
1 случай: Поворот
R и R \ ортонормированы
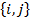
α – угол поворота системы координат
aij— координаты новых базисных векторов относительно старого базиса
В нашем случае это
2 случай: Системы координат ортонормированы (перенос системы координат на вектор)
3 случай: Поворот с переносом
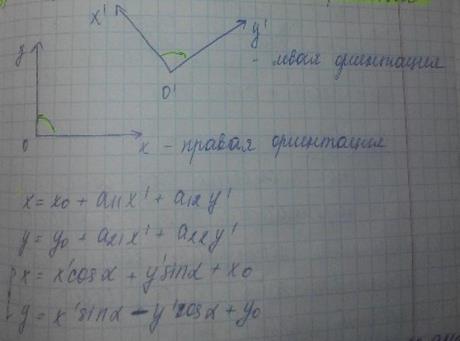
4 случай: Смена ориентации. Симметрия относительно оси
Угол идущий по часов стрелке будет отрицательной, стрелки будут отрицательными, если наоборот то положительными
3. Координаты вектора на плоскости. Сложение векторов, умножение вектора на число в координатах.
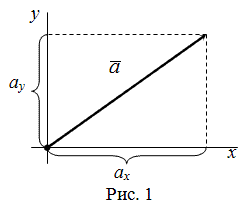
2. 
11.Применение свойств матриц и их определителей в задачах с экономическим содержанием. Примеры решения задач.
Предприятие производит три типа продукции, используя два вида ресурсов. Норма затрат ресурсов i-ого вида на производство единицы продукции j-ого типа задана матрицей затрат А, выпуск продукции за квартал- матрицей Х, стоимость единицы каждого вида ресурсов задана матрицей Р. Найти
1) Матрицу S полных затрат ресурсов каждого вида
2) Полную стоимость всех затраченных ресурсов
А= 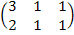
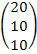
Полная стоимость ресурсов =
Полная стоимость ресурсов =
Завод производит швейные машины. Каждая машина может находиться в одном из двух состояний:
2) Требует регулировки.
В момент изготовления р% машин работают хорошо, (1-р)% требуют регулировки. Статистические исследования показали, что из тех машин, которые сегодня работают хорошо, через месяц 70% будут работать хорошо, а 30% потребуют регулировки. Среди тех машин, которые сегодня требуют регулировки, через месяц 60% будут работать хорошо, 40% потребуют регулировки. Каковы доли машин, которые будут работать хорошо или потребуют регулировки через месяц после их изготовления?
| Работают хорошо | Требуют регулировки | |
| Момент изготовления | 20% | 80% |
| Через месяц | ||
| Те что работали хорошо | 14% (20%*0.7) | 6% (20%*0.3) |
| Те что требовали регулировки | 48% (80%*0.6) | 32 (80%*0.4) |
| Итого через месяц: | 62% (14%+48%) | 38% (6%+32%) |
Ответ: через месяц 62% машин будут работать хорошо, а 32% будут требовать регулировки
_________________________________________________________________
Дана матрица прямых затрат А. Найти изменение векторов:
А) конечного продукта 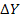
Б) валового выпуска 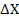
А) 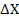
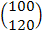
а)
а)
Найдем обратную матрицу. Для этого приведем матрицу A к единичной, а единичную матрицу теми же операциями к обратной.
1)
2)
3)
4)
5)
6)
Получили обратную матрицу:
Ответ: а) 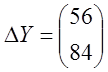
Решим систему методом Гаусса:
Оставим в левой части переменные x1 и x2, которые возьмем за основные. Оставшуюся (неосновную) переменную x3 перенесем в правую часть.
Отношения национальных доходов для сбалансированной торговли должно быть равно
Ответ:
8. 
2. Линейная зависимость и независимость векторов. Векторное пространство. Коллинеарность и компланарность векторов.
Свойства линейно зависимых векторов:
Линейное, или векторное пространство 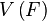
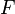
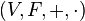
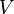
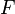

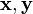
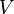
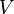
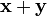
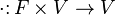
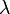
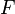
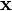
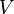
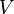
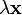
причём, заданные операции удовлетворяют следующим аксиомам — аксиомам линейного (векторного) пространства:
1. 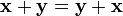

2. 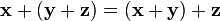
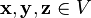
3. существует такой элемент 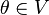
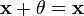
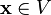
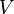
4. для любого 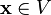
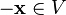
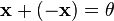
5. 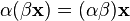
6. 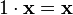
7. 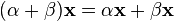
8. 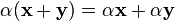
Таким образом, операция сложения задаёт на множестве 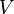
Векторные пространства, заданные на одном и том же множестве элементов, но над различными полями, будут различными векторными пространствами.
В качестве дополнительной (девятой) аксиомы векторного пространства иногда используют следующую: размерность пространства равна некоторому натуральному числу (если существует максимальная линейно независимая система векторов данного пространства или, что то же самое, существует конечная порождающая система векторов данного пространства), и тогда такое пространство называют конечномерным, или говорят, что пространство бесконечномерное (если не существует конечной порождающей системы векторов данного пространства). В соответствии с этим, теория линейных (векторных) пространств разделяется на две различные части: теорию конечномерных пространств, в которой существенным оказывается алгебраический аспект, и теорию бесконечномерных пространств, где главным оказывается аспект анализа — вопрос о разложимости данного элемента по заданной бесконечной системе функций.