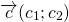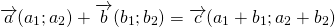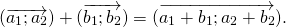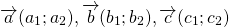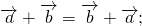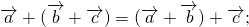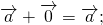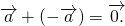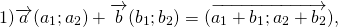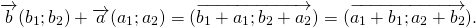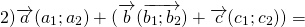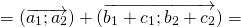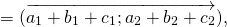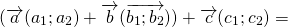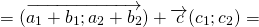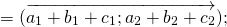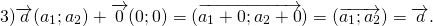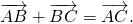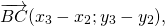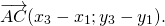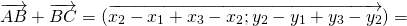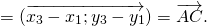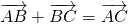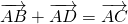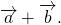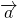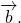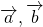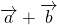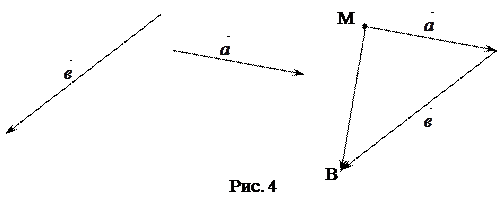В чем заключается правило треугольника
Геометрия. 9 класс
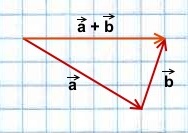
По правилу треугольника вектор (AC) ⃗ равен сумме векторов (AB) ⃗и (BC) ⃗. С другой стороны, вектор (AC) ⃗ равен сумме векторов (AD) ⃗ и (DС) ⃗.
(AC) ⃗ = (AB) ⃗+ (BC) ⃗ = a ⃗ + b ⃗.
(AC) ⃗ = (AD) ⃗ + (DC) ⃗ = b ⃗ +(a) ⃗.
a ⃗ + b ⃗= b ⃗ + (a) ⃗ (переместительный закон)
При доказательстве переместительного закона сложения векторов мы обосновали правило сложения неколлинеарных векторов – правило параллелограмма.
Чтобы сложить неколлинеарные векторы a ⃗ и b ⃗, нужно выбрать произвольную точку и отложить от неё векторы, равные данным. На этих векторах построить параллелограмм. Вектор с началом в выбранной точке и являющийся диагональю параллелограмма, будет суммой данных векторов a ⃗ и b ⃗.
Докажем ещё одно свойство сложения векторов: сочетательный закон.
Выберем произвольную точку А и отложим от неё вектор (AB) ⃗, равный(a) ⃗, от точки В – вектор (BC) ⃗, равный вектору b ⃗, а от точки С – вектор (CD) ⃗, равный вектору c ⃗.
Пользуясь правилом треугольника, найдём значения суммы трёх данных векторов.
(a ⃗ + b ⃗) + c ⃗ = (AB) ⃗+ (BC) ⃗ + (CD) ⃗ = (AC) ⃗ + (CD) ⃗ = (AD) ⃗.
Найдём сумму этих же векторов, изменив порядок действий.
Построим сумму векторов b ⃗ и c ⃗, а затем к вектору a ⃗ прибавим получившийся результат.
a ⃗+ (b ⃗+ c ⃗) = (AB) ⃗+ ((BC) ⃗ + (CD) ⃗) = (AB) ⃗ + (BD) ⃗ = (AD) ⃗.
Мы доказали, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.
При сложении нескольких векторов пользуются правилом многоугольника: при сложении векторов их последовательно откладывают один за другим, так чтобы начало следующего вектора совпадало с концом предыдущего. Вектор, соединяющий начало первого вектора с концом последнего, будет суммой данных векторов.
p ⃗ = (a1) ⃗+ (a2) ⃗ + (a3) ⃗ + (a4) ⃗+ (a5) ⃗
Сложение векторов
Сумма векторов
Свойства сложения векторов:
Для любых векторов
3) свойство прибавления нулевого вектора:
4) сумма противоположных векторов равна нулевому вектору:
Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:
Так как соответствующие координаты равны, то эти векторы равны.
(О сложении векторов)
Каковы бы ни были точки A, B, C, имеет место векторное равенство:
Что и требовалось доказать.
Правило треугольника построения суммы двух векторов
Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.
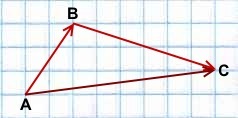
(то есть это правило следует из теоремы о сложении векторов).
Правило параллелограмма построения суммы двух векторов
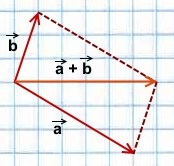
Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.
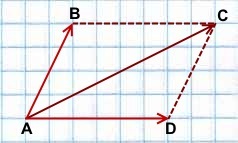
Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.
При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.
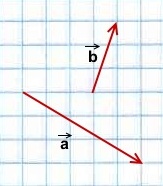
1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора
Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).
2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы
Достроим на этих векторах параллелограмм.
равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.
1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.
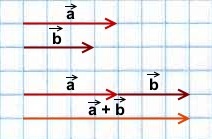
2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.
Фактически в обоих случаях мы используем правило треугольника сложения векторов:
от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.
Из неравенства треугольника следует ещё два свойства сложения векторов:
Сложение векторов
Часть математических и физических задач содержит необходимость математических действий с векторами (сложение и вычитание).
Способ 1. Метод сложения треугольником
Возьмём необходимые вектора и параллельным переносом совместим конец первого вектора ( ) и начало второго ( ) (рис. 1)
Рис. 1. Сложение векторов (правило треугольника)
Тогда вектор, соединяющий начальную точку первого вектора ( ) и конец второго ( ), является вектором ( ).
Способ 2. Метод сложения параллелограммом
Возьмём необходимые вектора и параллельным переносом совместим начало первого вектора ( ) и начало второго ( ) (рис. 2). Параллельным переносом совместим конец каждого вектора с началом другого.
Рис. 2. Сложение векторов (правило параллелограмма)
Тогда вектор, соединяющий общую начальную точку первого ( ) и второго ( ) векторов и общий конец данных векторов, является вектором суммы ( ).
Вывод: в ряде задач, где присутствуют несколько однородных векторных физических величин, часто необходимо найти общий вектор (общую скорость, равнодействующую силу, полный вектор магнитной индукции или электрической напряжённости поля). Тогда необходимо сначала сложить вектора, а потом найти модуль получившегося вектора.Чаще всего первый метод используется в кинематике (сложение скоростей). Второй метод часто используют в динамике.
Сложение и вычитание векторов
Существование: Имеем два следующих случая:
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
\( \vec + \vec = \left( <
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора \( \overrightarrow \) выполняется равенство
Для произвольных точек \( A,\ B\ и\ C \) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Разность векторов. Вычитание векторов
Длина нулевого вектора равна нулю:
\( \left| \vec <0>\right| = 0 \)
Умножение вектора на число
Определение Произведением вектора \( \overrightarrow
Длина вектора \( \overrightarrow
Векторы \( \overrightarrow
Правило треугольника
Чтобы сложить векторы 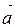
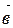
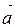
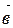
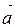
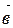
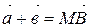
По правилу треугольника можно складывать любые векторы.
Коротко правило треугольника можно записать так:
для любых трех точек А,В и С 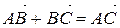
Правило параллелограмма
Чтобы сложить векторы 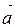
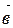
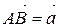
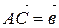
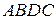
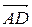
 |
По правилу параллелограмма можно складывать тольконеколлинеарные векторы.
Свойства сложения векторов:
Суммой n векторов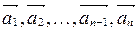
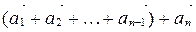
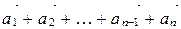
При построении суммы n векторов пользуются правилом многоугольника.
Дата добавления: 2015-11-28 ; просмотров: 3263 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ