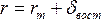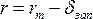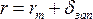В чем заключается суть зональной системы прямоугольных координат

Зональная система плоских прямоугольных координат

(проекция Гаусса – Крюгера)

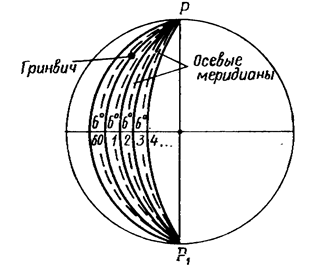
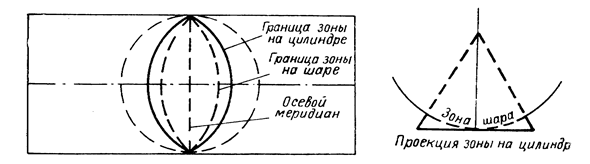
Эта проекция предложена Гауссом в 1828 г., удобные для практических расчетов формулы разработаны Крюгером к 1912 г., в СССР принята с 1928 г. Сущность проекции заключается в следующем. Поверхность земного сфероида делят меридианами на зоны в 6° по долготе, начиная от начального меридиана, и нумеруют по направлению к востоку (рис. 35), всего зон 60. Далее получают плоские изображения каждой зоны, для чего мысленно помещают сфероид внутрь цилиндра так, чтобы осевой меридиан зоны касался поверхности цилиндра (рис. 36). Из центра сфероида (рис. 37) зону проектируют на поверхность цилиндра – при этом углы сферы будут изображены без искажения, поэтому данную проекцию называют равноугольной, поперечно-цилиндрической. Изображение на поверхности цилиндра затем можно развернуть на плоскость.

В поперечно-цилиндрической проекции искажения будут в длинах линий: зоны на цилиндре получаются более широкими, чем на шаре. Не будет никаких искажений осевого меридиана – он касается поверхности цилиндра, но чем дальше расположены отрезки от осевого меридиана, тем больше искажений в длинах линий.

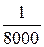
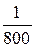
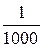
Ширина зоны на экваторе около 670 км, т.е. крайние точки зоны удалены от осевого меридиана примерно на 335 км. Искажения в длинах линий на экваторе достигают: при удалении от осевого меридиана на 100 км – , на 300 км – . Для широт территории РФ наибольшие искажения могут достигать примерно .

Наличие искажений в общем случае определяет возможное непостоянство масштаба в отдельных частях карты, и поэтому существуют понятия главного масштаба и частных масштабов. Главный – масштаб того глобуса, который изображают при составлении карты, частные масштабы относятся к различным частям карты.

Система географических координат удобна для изучения всей физической поверхности Земли или значительных ее участков, но неудобна для решения многих инженерных задач. Проекция Гаусса в географическом отношении не имеет практического значения, так как дает изображение земной поверхности с разрывами. Но ее ценность в том, что она в силу малых искажений сближает карту с планом и позволяет назначать систему плоских прямоугольных координат в каждой зоне, что удобно при решении инженерных задач.

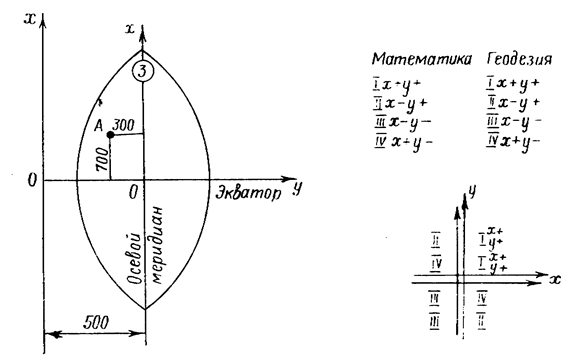
В проекции Гаусса за начало координат в каждой зоне принимают точку пересечения осевого меридиана с линией экватора, которые образуют прямой угол. Они и есть в данном случае оси координат (рис. 38). Осевой меридиан служит осью абсцисс x, а линия экватора – осью ординат у. Положительным направлением абсцисс считается направление от экватора к северу, положительным направлением ординат – на восток. В математике применяется левая система координат (нумерация четвертей против движения часовой стрелки), в геодезии – правая система. Но так как наименования осей координат тоже противоположны, знаки координат точек, расположенных в одноименных четвертях, совпадают (см. рис. 38), что позволяет применять формулы тригонометрии без всяких изменений и в данной системе.

Для территории РФ, расположенной в северном полушарии, абсциссы х везде положительны, а ординаты у могут быть и положительными, и отрицательными, например, для точки А (см. рис. 38) x_A = 700 км; y_A = – 300 км. Отрицательные ординаты затрудняют обработку геодезических материалов. Чтобы избежать этого, ординату осевого меридиана принимают не за 0, а за 500 км. Следовательно, к ординатам всех точек зоны прибавляется эта условная величина (500 км), и теперь у_А = – 300 + 500 = 200 км.

Дополнительно в записи ординаты точки указывают номер зоны в связи с тем, что во всех шестидесяти зонах системы координат одинаковые. Следовательно, значение координат точки необходимо дополнить номером зоны, в которой эта точка находится. Этот номер приписывается впереди ординаты, и если в нашем случае точка А (см. рис. 38) находится в третьей зоне, то запись ординаты будет у_А = 3200 км.

Таким образом, ординаты точек получают преобразования и соответственно называются преобразованными. Для определения местоположения точки в зоне следует, зная ее координаты, действовать в обратном порядке: убрать из записи ординаты номер зоны и вычесть 500 км.

Источник

ЗОНАЛЬНАЯ СИСТЕМА ПРЯМОУГОЛЬНЫХ КООРДИНАТ

Географические координаты могут быть распространены на всю по­верхность земного эллипсоида. В этом их большое достоинство. Однако их применение в массовых геодезических работах затруднительно, по­скольку оно связано со сложными вычислениями. Поэтому эти координа­ты применяют при картографировании, навигации, создании и использо­вании геоинформационных систем (ГИС) и т. д.

В инженерной геодезии в связи с этим используют плоские прямо­угольные координаты. Для установления связи между географическими координатами любой точки на земном сфероиде и прямоугольными коор­динатами той же точки на плоскости применяют специальный способ проектирования всего земного шара на плоскость по шестиградусным зо­нам, простирающимся от северного полюса к южному (рис. 2.4).

Счет зон ведут на восток от нулевого, проходящего через Гринвиче-скую обсерваторию, меридиана. Каждую полученную таким образом зо­ну проектируют поочередно на плоскость при помощи цилиндра.

Если общую фигуру Земли представить в виде сферы, то ось АВ тако­го цилиндра будет проходить через центр сферы О (рис. 2.5). При этом

ось вращения Земли РР\ будет пер­пендикулярна оси цилиндра АВ, и каждая зона будет касаться повер­хности цилиндра по своему средне­му меридиану.

Каждую зону последовательно проектируют на внутреннюю боко­вую поверхность цилиндра при ус­ловии сохранения равенства углов, формы и подобия изображаемых контуров. Зоны переходят на повер­хность цилиндра в несколько рас­ширенном виде (см. рис. 2.5) и, раз­вернув цилиндр, получают плоское изображение земной поверхности. Такую проекцию поэтому называ­ют равноугольной поперечно-цилиндрической (рис. 2.6). Она дает не сплошное изображение всей земной поверхности, а с разрывами, увели­чивающимися от экватора к полюсам.

Север

Рис. 2.5. Схема к построению равноугольной поперечно-цилиндрической проекции

В этой системе начало координат в каждой зоне принимают в точке пересечения среднего меридиана с экватором (рис.2.7). Средний мериди­ан зоны принимают за ось абсцисс, поэтому его называют еще осевым ме­ридианом. Изображение экватора в виде прямой, перпендикулярной осе­вому меридиану, принимают за ось ординат.

Абсциссы к северу от экватора принимают положительными, а к югу — отрицательными. Ординаты, отсчитываемые на восток от осевого ме­ридиана, считают положительными, а на запад — отрицательными.

Источник

Зональная система плоских прямоугольных координат

(проекция Гаусса – Крюгера)

Зональная система плоских прямоугольных координат предложена Гауссом в 1828 г., удобные для практических расчетов формулы разработаны Крюгером к 1912 г., в СССР принята с 1928 г. Сущность проекции заключается в следующем. Поверхность земного сфероида делят меридианами на зоны в 6° по долготе, начиная от начального меридиана, и нумеруют по направлению к востоку (рис. 35), всего зон 60. Далее получают плоские изображения каждой зоны, для чего мысленно помещают сфероид внутрь цилиндра так, чтобы осевой меридиан зоны касался поверхности цилиндра (рис. 36). Из центра сфероида (рис. 37) зону проектируют на поверхность цилиндра – при этом углы сферы будут изображены без искажения, поэтому данную проекцию называют равноугольной, поперечно-цилиндрической. Изображение на поверхности цилиндра затем можно развернуть на плоскость.

В поперечно-цилиндрической проекции искажения будут в длинах линий: зоны на цилиндре получаются более широкими, чем на шаре. Не будет никаких искажений осевого меридиана – он касается поверхности цилиндра, но чем дальше расположены отрезки от осевого меридиана, тем больше искажений в длинах линий.

Ширина зоны на экваторе около 670 км, т.е. крайние точки зоны удалены от осевого меридиана примерно на 335 км. Искажения в длинах линий на экваторе достигают: при удалении от осевого меридиана на 100 км – , на 300 км – . Для широт территории РФ наибольшие искажения могут достигать примерно .

Наличие искажений в общем случае определяет возможное непостоянство масштаба в отдельных частях карты, и поэтому существуют понятия главного масштаба и частных масштабов. Главный – масштаб того глобуса, который изображают при составлении карты, частные масштабы относятся к различным частям карты.

Система географических координат удобна для изучения всей физической поверхности Земли или значительных ее участков, но неудобна для решения многих инженерных задач. Проекция Гаусса в географическом отношении не имеет практического значения, так как дает изображение земной поверхности с разрывами. Но ее ценность в том, что она в силу малых искажений сближает карту с планом и позволяет назначать систему плоских прямоугольных координат в каждой зоне, что удобно при решении инженерных задач.

В проекции Гаусса за начало координат в каждой зоне принимают точку пересечения осевого меридиана с линией экватора, которые образуют прямой угол. Они и есть в данном случае оси координат (рис. 38). Осевой меридиан служит осью абсцисс x, а линия экватора – осью ординат у. Положительным направлением абсцисс считается направление от экватора к северу, положительным направлением ординат – на восток. В математике применяется левая система координат (нумерация четвертей против движения часовой стрелки), в геодезии – правая система. Но так как наименования осей координат тоже противоположны, знаки координат точек, расположенных в одноименных четвертях, совпадают (см. рис. 38), что позволяет применять формулы тригонометрии без всяких изменений и в данной системе.

Для территории РФ, расположенной в северном полушарии, абсциссы х везде положительны, а ординаты у могут быть и положительными, и отрицательными, например, для точки А (см. рис. 38) x_A = 700 км; y_A = – 300 км. Отрицательные ординаты затрудняют обработку геодезических материалов. Чтобы избежать этого, ординату осевого меридиана принимают не за 0, а за 500 км. Следовательно, к ординатам всех точек зоны прибавляется эта условная величина (500 км), и теперь у_А = – 300 + 500 = 200 км.

Дополнительно в записи ординаты точки указывают номер зоны в связи с тем, что во всех шестидесяти зонах системы координат одинаковые. Следовательно, значение координат точки необходимо дополнить номером зоны, в которой эта точка находится. Этот номер приписывается впереди ординаты, и если в нашем случае точка А (см. рис. 38) находится в третьей зоне, то запись ординаты будет у_А = 3200 км.

Таким образом, ординаты точек получают преобразования и соответственно называются преобразованными. Для определения местоположения точки в зоне следует, зная ее координаты, действовать в обратном порядке: убрать из записи ординаты номер зоны и вычесть 500 км.

Практическая часть

Освоение обозначений систем координат на учебной топографической карте масштаба 1:10 000 и определение координат точек

Географическая система координат. Лист карты окаймляют три рамки: внутренняя, минутная и внешняя. Внутренняя рамка имеет форму трапеции (что наглядно видно на картах более мелкого масштаба). Эта рамка образована отрезками меридианов и параллелей, непосредственно ограничивающих картографическое изображение. На выходах этих линий в углах рамки указаны соответствующие значения широты и долготы. Так, на рис. 39,а лист карты ограничен по долготе 14°11¢15² – 14°15¢00² и по широте 54°17¢30² – 54°20¢.

Минутная рамка с обозначением определенного интервала широт и долгот служит для более точного измерения географических координат точек на карте. Минутные и полуминутные интервалы отмечены утолщенными линиями, десятисекундные интервалы – точками. Соответственно на рисунке начало первых утолщенных линий определяет точку с долготой l = 14°12¢ и с широтой j = 54°18¢. Внешняя рамка имеет декоративное назначение.

Широта j_B и долгота l_B точки В, заданной на карте, определяется параллелью и меридианом, проходящим через эту точку. Для определения j_B и l_B, без построения линий параллели и меридиана через данную точку, следует соединить прямыми линиями одноименные концы минутных или десятисекундных интервалов, далее применить линейную интерполяцию, для чего положить линейку с миллиметровыми делениями так, чтобы отсчитать отрезки a и b (рис. 39, б). Тогда

.

На рис. 38,а для точки В j₁ = 54°19¢40²; j₂ = 54°19¢50²;
j_B = 54°19¢40² + 10² = 54°19¢48². Аналогично, проведя меридианы l₁и l₂ (рис. 39, б), определите долготу l_B. Для контроля j и l нужно вычислять дважды, при двух различных положениях линейки, т.е. при различных значениях отрезков а и b. Далее следует определить географические координаты двух точек. Вначале определите координаты точек на глаз, затем для одной из точек уточните координаты по приведенному выше способу (для соединения одноименных интервалов потребуется линейка длиной более 40 см).

Прямоугольная система координат Гаусса–Крюгера. В этой системе координаты на листе карты представлены сеткой квадратов (см. рис. 39, а). Размер квадрата должен быть кратным целому числу километров, поэтому сетка называется километровой (линии сетки 1, 2 на рис. 39, а).

Абсциссы х, за начало отсчета которых принимают линию экватора, подписаны у горизонтальных линий, при этом сотни километров приводятся не у всех линий. Например, абсцисса 6019 выписана полностью, у абсциссы 6020 приведена только цифра 20 («сокращенная абсцисса»). Система надписей у ординат аналогична, при этом ординаты точек указываются преобразованными.

При обозначении квадратов километровой сетки применяются сокращенные координаты (квадраты 22/48; 21/49 и т.д. на рис. 39, а).

Для получения значений координат точки D измеряют отрезки Dx_ю и Dу_з, от южной и западной сторон квадрата километровой сетки. Для контроля проводят аналогичные измерения от северной и восточной сторон квадрата: Dx_с и Dу_в.

Сторона километровой сетки равна 1000 м, и потому разности
f_x = (Dx_ю + Dx_с) – 1000 и f_y = (Dу_з + Dу_в) – 1000 представляют собой погрешности в определении координат. Точность измерения считается достаточной, если f_x и f_y [м] не превосходят числа тысяч в знаменателе численного масштаба карты. В этом случае f_x и f_y распределяются с обратным знаком, пропорционально измеренным величинам Dx и Dу.

Пусть для точки D (квадрат 22/50) получено: x_D = 6022,75 км и у_D = = 3450,32 км. Действительное значение ординаты будет y_{Dдейств} = 450,32 – –500 = – 49,68 км[1]. Точка D расположена в 3-й зоне, находится западнее осевого меридиана (рис. 39, в).

Упражнения.Найдите координаты двух точек при условии первоначального определения на глаз. Затем для одной точки уточните координаты измерениями, определите по приведенному ранее способу погрешности и распределите их. Для этой же точки вычислите действительное значение ординаты, покажите ее местоположение на схеме зоны.

ОРИЕНТИРОВАНИЕ ЛИНИЙ, ПЛАНОВ И КАРТ

Для ориентирования карты достаточно ориентировать линию, принадлежащую данной карте.

Для того чтобы ориентировать линию, надо знать угол ориентирования, т.е. тот угол, который данная линия составляет с направлением, принятым за начальное.

В географической системе за начальное направление принято северное направление географического меридиана (рис. 40, 41) и углами ориентирования являются географический азимут A и географический румб r_г.

Географический азимут – угол, отсчитываемый от северного направления географического меридиана по ходу часовой стрелки до ориентируемой линии. Изменяется от 0 до 360°.

Но географические меридианы в разных точках сфероида не параллельны между собой, поэтому азимут одной и той же линии (см. рис. 40, линия 1–2) в различных ее точках будет различен (азимут A_(A)в точке А не равен азимуту A_(B) в точке В. Это различие определяет угол g, который называется сближением меридианов: g = А_(В) – А_(А)(см. рис. 40, 41).

В геодезии пользуются терминами: прямое направление линии и обратное. Так, если исходное направление линии – направление АВ
(см. рис. 41), то обратное направление – направление ВА. Соответственно азимут линии АВ будет прямым, линии ВА – обратным (т.е. А_(А), А_(В) – азимуты прямые, А_(В)обр – азимут обратный). Зная азимут прямой в точке А_(А)и сближение меридианов g_(В),можно вычислить азимут обратный в точке В. В данном случае А_(В)обр = А_(А) + 180° + g_(В).

Расчет показал, что для средних широт при расстояниях между точками менее 0,5 км сближение меридианов менее 30². В строительной практике такая погрешность (30²) в определении направлений считается допустимой, и тогда при l

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник

Зональная система координат

Из перечисленных выше систем координат, только географическая может быть распространена на всю земную поверхность. Однако использование ее весьма затруднено ввиду сложности решения ряда технических задач на сфере, т.к. географические координаты выражаются в градусной мере, тогда как все расстояния на земной поверхности определяются в метрах. Значительно проще решаются эти задачи в удобной системе плоских прямоугольных координат.

Для установления связи между географическими координатами любой точки на сфероиде и прямоугольными координатами этой же точки на плоскости применяют зональную систему координат. Эта система основана на равноугольной (конформной) поперечно-цилиндрической проекции Гаусса и называется системой координат Гаусса-Крюгера.

Сущность этой проекции заключается в следующем.

1.Земной эллипсоид меридианами разбивается на шести и трехградусные зоны. Средний меридиан называют осевым. Нумерация зон ведется на восток. Осевые меридианы лежат на внутренней поверхности цилиндра, в котором сферическая поверхность разбивается на отдельные участки(всего 60).

2.Каждая зона в отдельности конфермно проектируется на плоскость таким образом, чтобы осевой меридиан изображался прямой линией без искажений (т.е. с точным сохранением длин вдоль осевого меридиана). Экватор также изобразится прямой линией. За начало счета координат в каждой зоне принимается пересечение изображения осевого меридиана – оси абсциссе х и экватора – оси ординат у. Линии, параллельные осевому меридиану и экватору образуют прямоугольную координатную сетку.

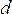
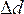
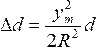
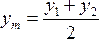
3.Искажения длин линии в проекции Гаусса-Крюгера возрастают по мере удаления от осевого меридиана пропорционально квадрату ординаты. Эти искажения на краях шестиградусной зоны могут достигать величины порядка 1/1500 длины линии, а в трехградусной зоне 1/6000. Для отрезка с координатами конечных точек х1у1 и х2у2, формула поправки за искажение длины линии на плоскости имеет вид , где и R- средний радиус кривизны.

В съемках крупного масштаба такими искажениями пренебрегать нельзя. В этом случае, при расположении участка на краю зоны, следует или учитывать искажения, или применять частную систему координат с осевым меридианом, проходящим примерно через середину участка работ.

4.Система координат в каждой зоне одинаковая. Для установления зоны, к которой относится точка, к значению ординат слева приписывается номер зоны. Чтобы не иметь отрицательных ординат, точкам осевого меридиана условно приписывается ордината, равная 500 км. Например, если дана ордината 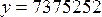, то точка находится в 7 зоне и имеет ординату от осевого меридиана равную 375252-500000=-124748 м.

Листы международной карты мира масштаба 1:1 000 000 представляют трапеции, ограниченные с востока и запада прямыми – крайним меридианами, а с севера и юга – дугами окружностей – крайними параллелями. Каждый лист такой карты до60 широты имеет размеры: 4 по широте и6 по долготе. Начиная от Гринвича через каждые 6 земной поверхности делится на 60 колонн. Нумерация колонн начинается от меридиана 180 и ведется против часовой стрелки. Например колонна №34 ограничена меридианами 18 и 24 в.д. Номер зоны равен номеру колонны 30. По широте земная поверхность от экватора через каждые4 делится на гряды, обозначается заглавными буквами латинского алфавита от A до V.

Система обозначения отдельных листов карт называется номенклатурой карт. Деление листа карты одного масштаба на листы карты более крупного масштаба называется разграфкой топографических карт.

1:500 000 – на 4 части – L-36-Б

1:200 000 – на 36 листов – L-36-XXXII

1:100 000 – на 144 листа – L-36-84

1:50 000 – лист 1:100 000 на 4 части – L-36-84-A

1:25 000 – на 4 части – L-36-84-A-в

1:10 000 – на 4 части – L-36-84-A-в-3

Для более крупного масштаба разграфка будет показана на практических занятиях.

Ориентировать линию на плоскости – значит определить ее положение относительно направления, принятого за начальное(т.е. меридиана).

Для ориентирования направлений по сторонам света пользуются азимутами и румбами.

Взаимоотношение румбов и дирекционных углов хорошо иллюстрируют рисунок и таблица.

Сближение меридианов. Прямые и обратные азимуты и румбы.

За счет сферичности Земли, меридианы на полюсах сходятся в точки. Линия, касательная к дуге меридиана в данной точке, называется полуденной линией этой точки.

Угол между полуденными линиями двух точек, лежащих на разных меридианах, называется сближением меридианом в данных точках.

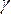
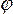
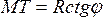
Для приближенного определения сближения меридианов представим земной шар радиусом R и две точки M и N, лежащие на одной параллели, через которые проведены меридианы. Если в точках M и N провести касательные к этим меридианам – полуденные линии, то они пересекутся на продолжении оси вращения Земли в точке Т под углом , называемым сближением меридианов в точках M и N. Если точки M и N имеют широту равную , то радиус ОМ, согласно рисунку будет , а касательная .

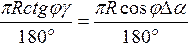
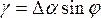
Подставляя в эти формулы значения r и MT получим , откуда имеем приближенно , т.е. сближения двух меридианов равняется разности их долгот, умноженной на синус широты.

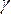
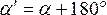
Если через точку Р, являющуюся началом линии PQ, проходит географический меридиан СЮ и линия NS параллельная осевому меридиану зоны, в которой лежит точка Р, то угол между ними будет углом сближения меридианов, а — дирекционным углом линии PQ, отсюда . Для линии PQ угол будет прямым дирекционным углом, а — обратным. Так как линии NS параллельны осевому меридиану, то . Сближение меридиан точек расположенных к востоку от осевого меридиана имеет знак (+), к зададу (-).

Прямые и обратные румбы.

Из рисунка хорошо видно соотношение прямого и обратного румбов линии DF значения r будут иметь одинаковое градусное значение, обозначения – противоположение (например ЮВ-СЗ; СВ-ЮЗ; и т.д.).

Магнитные азимуты(объяснить земной магнетизм).

Вертикальная плоскость, проходящая через концы магнитной стрелки называется плоскостью магнитного меридиана, угол которого она составляет с плоскостью географического меридиана, называется магнитным склонением, обозначается через 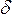(дельта). Магнитные азимуты отсчитываются от северного направления магнитной стрелки(от0 до 360 ).

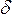
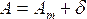
Если склонение восточное, то, чтобы перейти от магнитного азимута к географическому азимуту, значение берется со знаком «+», т.е. , если склонение западное, то со знаком «-».

Зависимость между географическими и магнитными румбами приведена в таблице.

При восточном склонении

СВ

ЮВ

ЮЗ

СЗ

При западном склонении

СВ

ЮВ

ЮЗ

СЗ

1.Рельеф земной поверхности

Физическая поверхность Земли неровная, на ней имеются возвышения, углубления и сравнительно плоские участки образующие рельеф. Следовательно, рельефом называется совокупность различных по форме неровностей (понижений и повышений) земной поверхности. Рельеф исключительно сложен для изображения. Сложность проистекает из того, что рельеф – пространственный объект, и мы его обычно рассматриваем ортогонально на плоскости. Рельеф местности – важнейший элемент содержания топографических карт.

Все формы земной поверхности, представляющие сочетание его элементов, можно разделить на положительные (выпуклые) и отрицательные (вогнутые).

Главные положительные формы рельефа следующие

Курган – изолированная, расположенная на равнине возвышенность до 50 м высотой с резко выраженной подошвой.

Бугор – отдельная куполообразная или коническая возвышенность высотой до 100 м с резко выраженной подошвой.

Холм – отдельная небольшая коническая или куполообразная возвышенность высотой не более 200 м, с пологими склонами и с неясно выраженной подошвой.

Гора – изолированная возвышенность высотой более 200 м с ясно выраженными и сравнительно крутыми склонами. У горы следует различать вершину, склоны и подошву. Остроконечная вершина горы называется пиком.

Седловина – понижение между двумя соседними вершинами или возвышенностями, напоминающее своей формой седло.

Хребет – горная возвышенность, имеющая сравнительно большое протяжение, с крутыми склонами. У хребта различают: водораздел – он проходит по самым высоким точкам хребта, называемым гребнем(его профиль представляет волнообразную кривую или ломаную линию); перевалы – пониженные части на профиле водораздела; два склона хребта, один из которых часто бывает более крутой; отроги хребта – второстепенные, меньше по размерам хребты, отходящие от главного водораздела и являющиеся местом перехода к равнине.

Плато – плоская широкая возвышенность, ограниченная крутыми склонами.

К главным отрицательным формам рельефа относят

Овраг – резко выраженное углубление на равнине, вытянутое в одном направлении, с крутыми склонами и временно действующими водотоками. Овраги часто имеют ответвления.

Балка – углубление более крупное, чем овраг, с пологими склонами, зачастую покрытыми растительностью.

Лощина – небольшое углубление с весьма пологими склонами, постепенно переходящими в равнину. У лощины, оврага и балки различают два склона – боковые стороны – и тальвег – линию, соединяющую самые низкие точки дна углублений и имеющую уклон в одном направлении.

Долина – выработанное рекой понижение, вытянутое в одном направлении, часто имеющее ясно выраженные склоны. Тальвег долин, как и лощина, имеет уклон в одном направлении.

Ущелье – узкая скалистая долина со сходящимися внизу склонами.

Котловина – вынутое понижение рельефа на земной поверхности, ограниченное со всех сторон (замкнутая котловина) или расположенное между горными цепями (межгорная котловина). Котловины бывают различной величины и формы (чашеобразные, блюдцеобразные и др). У котловины различают: край – место перехода котловины в равнину; дно – наиболее низкую часть котловины, поднимающиеся от дна к краям. Небольшие по размерам и мелкие по глубине котловины с плоским дном называются блюдцами или западинами.

2.Абсолютные и относительные высоты точек земной поверхности, превышения, уклоны.

Для полного определения положения точки на физической поверхности Земли нужно кроме координат указать высоту точки или расстояние от нее до уровенной поверхности по отвесной линии. Численное значение высоты называется отметкой. Высоты бывают абсолютные и относительные, или условные. Счет абсолютных высот ведется от поверхности геоида, т.е. от среднего уровня мирового океана, например, высоты точек С-НС и В-Н В. Наблюдение за средним уровнем океана ведется при помощи футштока на водомерном мосту. В странах СНГ счет абсолютных высот ведется от нуля Кранштадского футштока (Балтийская система высот).

Высота одной точки относительно уровенной поверхности другой точки называется относительной отметкой или превышением h этих точек, т.е. превышение равно разности высот двух точек.

Началом счета высот может являться любая условно принятая уровенная поверхность, например отрезок НВ называется относительной высотой.

В зависимости от абсолютного значения высот точек и их взаимного расположения различают равнинную, холмистую и горную местности.

На равнинной местности крутизна склона мало заметна, отсутствуют резко выраженные неровности, а отдельные точки ее имеют небольшие относительные высоты. Горная местность характеризуется сочетанием понижений и возвышенностей высотой более 200 м и резко выраженными крутыми склонами.

Изображение рельефа на планах и картах

Рельеф на планово-картографических материалах изображают при помощи соответствующих условных знаков, от которых требуется:

· подробно и точно показать расположение всех его форм неровностей местности, характеризующих ее расчлененность и доступность;

· обеспечить определение высот отдельных точек местности и превышений одних точек над другими, направление склонов и их крутизну;

· наглядно изобразить рельеф, позволяя возможно яснее представить действительный ландшафт местности.

Для изображения рельефа на планах и картах используются способы: штрихов, отмывки и горизонталей.

При штриховом изображении рельефа густота и толщина штрихов (гашюр) усиливается с увеличением крутизны скатов. Способ наглядный.

Недостаток этого способа в том, что по плану с штриховками трудно судить о превышении между точками земной поверхности. Кроме того, обилие штрихов ухудшает читаемость планов и карт, а само нанесение штрихов – очень трудоемкая и кропотливая работа.

Наглядными способами изображения рельефа является способ отмывки скатов, т.е. окрашивание скатов коричневой краской по принципу: чем круче скат, тем темнее тон окраски, и способ цветовой пластики, применяемый для изображения рельефа на географических картах. Например на физико-географических картах низменности показаны зеленым цветом, возвышенность светло-коричневым, горы – темно-коричневым.

Способы отмывки и цветной пластики, как и метод штрихов, не дают точного представления о превышениях между точками земной поверхности, а главное, недостаточное для инженерных целей точностью.

На современных топографических картах и планах рельеф изображают горизонталями, дополненными абсолютными отметками и бергштрихами. Этот способ объективен, прост для использования, позволяет геометрически наиболее точно передать форму рельефа и отобразить его особенности. Горизонталью называется след от пересечения физической поверхности Земли уровенной плоскостью, следовательно – горизонталь есть замкнутая кривая линия, изображающая геометрическое место точек земной поверхности с одинаковыми высотами.

Расстояние между параллельными секущими плоскостями должно быть одинаковым, их принято обозначать h малая и называть высотой сечения рельефа.

На топографических картах высота сечения рельефа устанавливается от масштаба съемки и от характера местнос

Стандартное (нормальное) сечение рельефа – 2% от показателя масштаба в метрах.

Масштабы карт и планов и высота сечения h в метрах

Источник