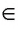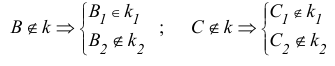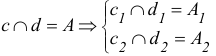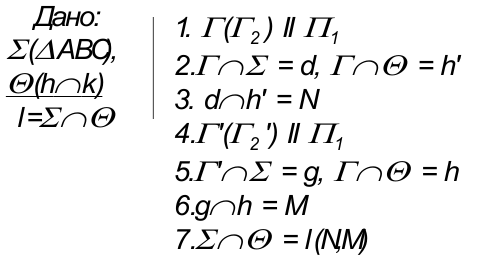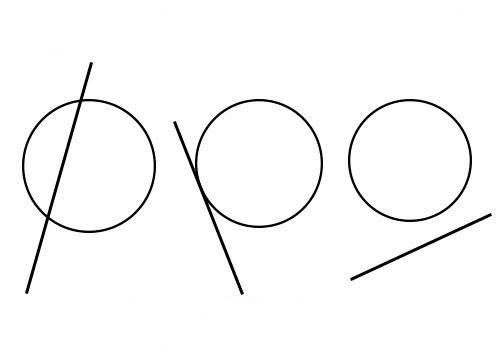В чем заключается свойство взаимного расположения точек на плоскости относительно данной прямой

Система геометрических понятий, изучаемых в школе. Основные свойства принадлежности точек и прямых, взаимного расположения точек на плоскости и прямой.

Рассмотрим пять групп аксиом, лежащих в основе евклидовой геометрии.

Первая группа – аксиомы принадлежности. В них устанавливаются отношения между точками, прямыми и плоскостями.

1. Через две точки проходит одна и только одна прямая.

2. На каждой прямой лежат по крайней мере две точки.

3. Существуют три точки, не лежащие на одной прямой.

Бесконечность прямой надо будет доказывать.

Для построения стереометрии присоединяются еще аксиомы.

4. Через каждые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.

5. Если две точки прямой принадлежат некоторой плоскости, то и все точки этой прямой принадлежат указанной плоскости.

6. Если две плоскости имеют общую точку, то они имеют по крайней мере еще одну общую точку.

7. Существует по крайней мере 4 точки, не лежащие в одной плоскости.

Вторая группа – аксиомы порядка. Они определяют понятие «лежать между» и выражают свойства взаимного расположения точек на прямой и плоскости.

1. Если точка В лежит между точками А и С, то она лежит между точками С и А.

2. Для любых двух точек прямой А и В существует на этой прямой такая точка С, что точка В лежит между точками А и С.

3. Из трех точек на прямой не более чем одна лежит между двумя другими.

4. Пусть точки А, В и С не лежат на одной прямой, и прямая не проходит ни через одну их этих точек. Если при этом прямая а пересекает отрезок АВ (то есть проходит через точку, лежащую между точками А и В), то она пересекает один из отрезков ВС или АС.

Аксиомы первых двух групп позволяют определить понятие отрезка, луча, угла.

Точки, расположенные между А и В, называются точками, лежащими внутри отрезка АВ, точки А и В называются концами отрезка АВ,

Луч с началом О – это совокупность всех точек прямой, лежащих с одной стороны от О.

Угол – это совокупность двух лучей с общим началом, лежащих на разных прямых.

Третья группа – аксиомы равенства (конгруэнтности). Они определяют равенство отрезков и углов.

1. На данной прямой по данную сторону от данной на ней точки можно отложить отрезок, равный данному, и притом единственным образом.

2. Два отрезка, порознь равны третьему, равны между собой.

3. Пусть на некоторой прямой точка В лежит между точками А и С и на некоторой другой или той же прямой точка В лежит между двумя точками А и С. Если при этом отрезок АВ равен отрезку А В и отрезок ВС равен В С, то АС = А С.

4. По одну сторону от данного луча можно отложить данный угол и притом единственным образом.

5. Два угла, порознь равные третьему, равны между собой.

Дата добавления: 2016-05-11 ; просмотров: 1334 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

На уроках математики в предыдущих классах и в главе 1 вы уже познакомились со свойствами некоторых геометрических фигур. Теперь вы приступаете к систематическому изучению геометрии.

Как уже отмечалось ранее, основными геометрическими фигурами являются точка, прямая, плоскость. Представление об этих фигурах вы уже имеете.

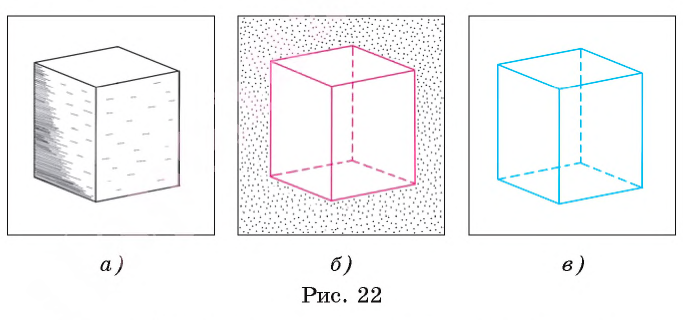
Например, туго натянутая нить дает представление о части прямой, страница книги или грань прямоугольного параллелепипеда — о части плоскости (рис. 22, а, б, в).

Если точка А принадлежит прямой b, то говорят, что прямая b проходит через точку А. Это записывают так: А

Если точка А не принадлежит прямой b, то говорят, что прямая b не проходит через точку А. В этом случае используется запись А 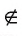b (читают: «Точка А не принадлежит прямой b», «Точка А не лежит на прямой b» или «Прямая b не проходит через точку А»).

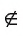
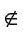
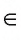
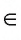
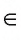
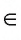
Например, на рисунке 23, а изображены точка С — вершина квадрата и точка Т, не лежащие на прямой l (С l, Т l), проходящей через вершины А и D квадрата (А l, D l). На рисунке 23, б, в изображена прямая l, проходящая через вершины О и F куба (O l, F l).

В курсе геометрии понятия « точка», « прямая» и «плоскость» относятся к основным понятиям и принимаются без определений, другие геометрические понятия определяются через основные. К основным понятиям относятся также понятия «принадлежать» и «лежать между». Свойства геометрических фигур устанавливаются путем логических рассуждений на основе некоторых утверждений (аксиом), которые принимаются без доказательств. Аксиомы выражают основные свойства геометрических фигур, которые соответствуют формам и отношениям, наблюдаемым в окружающем пространстве.

Утверждение, которое обосновывается путем логических рассуждений, называется теоремой, а само обоснование — доказательством. Доказать теорему — это значит путем рассуждений обосновать, что она следует из некоторых аксиом или ранее доказанных теорем.

Взаимное расположение точек и прямых на плоскости характеризуют следующие основные свойства (аксиомы):

Прямая, которая проходит через точки А и В, обозначается АВ или ВА.

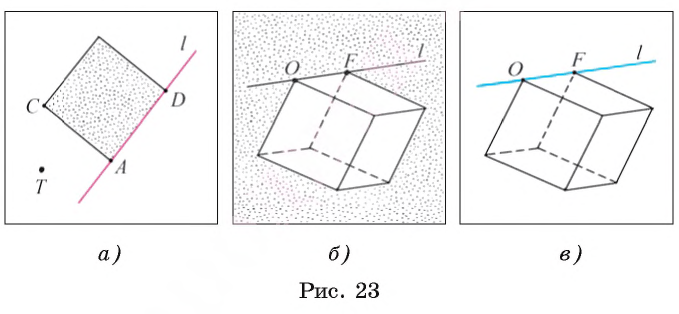
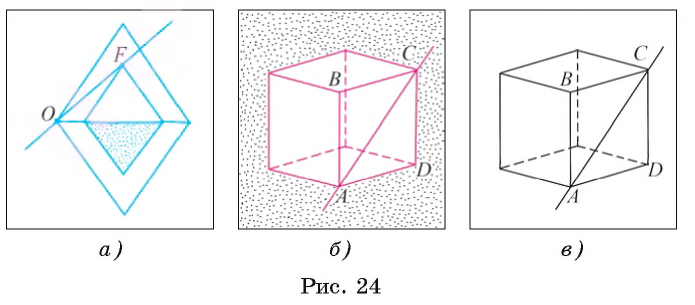
Например, на рисунке 24, а изображена прямая ОF, которая проходит через точки О и F, а на рисунке 24, б, в показана прямая АС, которая проходит через вершины А и С куба и лежит в той же плоскости, что и грань АВСD куба.

1 Здесь и в дальнейшем, говоря «две точки», «две прямые» и т. д., будем считать, что эти точки, прямые и т. д. различны.

Пересекающиеся и параллельные прямые

Рассмотрим понятия пересекающихся и параллельных прямых.

Определение. Две прямые называются пересекающимися, если они имеют одну общую точку.

Если прямые а и b пересекаются в точке О, то это обозначается так: О = а b (читают: «Прямые а и b пересекаются в точке О»).

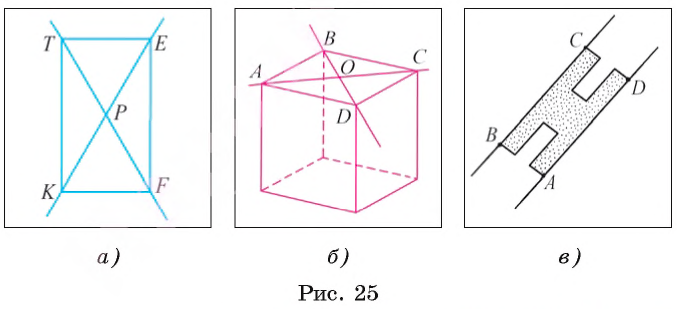
Например, на рисунке 25, а изображены прямые КЕ и TF, которые проходят через вершины прямоугольника и пересекаются в точке Р (Р =TF КЕ).

На рисунке 25, B изображены прямые АС и BD, которые проходят через вершины куба и пересекаются в точке О (О = АС 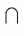ВD).

Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.

Параллельные прямые l₁ и l₂ обозначаются так: l₁ 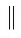l₂ (читают: «Прямая l₁ параллельна прямой l₂ »).

Например, на рисунке 25, в изображены параллельные прямые ВС и АD (ВС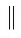АD).

Теорема. Если две прямые плоскости имеют общую точку, то она единственная.

Пусть две прямые а и b имеют общую точку О. Докажем, что других общих точек эти прямые не имеют. Допустим, что прямые а и b имеют еще одну общую точку O₁. Тогда получается, что через точки O и O₁ проходят две прямые а и b. Но этого быть не может, так как по аксиоме А3 через две точки проходит единственная прямая. Таким образом, наше предположение неверно, и прямые а и b имеют единственную общую точку.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Взаимное расположение точки, прямых и плоскостей с примерами

Содержание:

Взаимное расположение точки и прямой:

Возможны два варианта расположения точки относительно прямой:

Взаимное расположение прямых

Прямые в пространстве могут занимать друг к другу одно из трех положений:

Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.

Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.

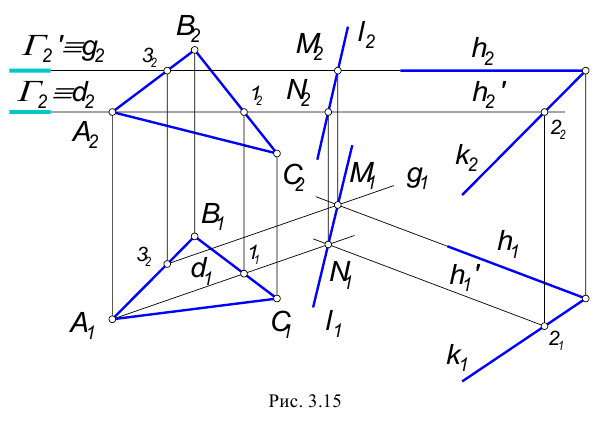
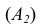
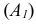
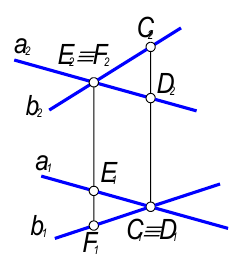
У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная и горизонтальная проекции этой точки должны находиться на одной линии связи.

Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.

Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.

На рис. 3.4 точка С принадлежит прямой b, а точка D на прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций.

Плоскость. Способы ее задания, положение относительно плоскостей проекций

Положение плоскости в пространстве может быть однозначно определено:

Всегда от одного способа задания плоскостей можно перейти к другому.

След плоскости – это линия пересечения заданной плоскости с одной из плоскостей проекций.

Соответственно различают горизонтальный, фронтальный и профильный следы плоскости.

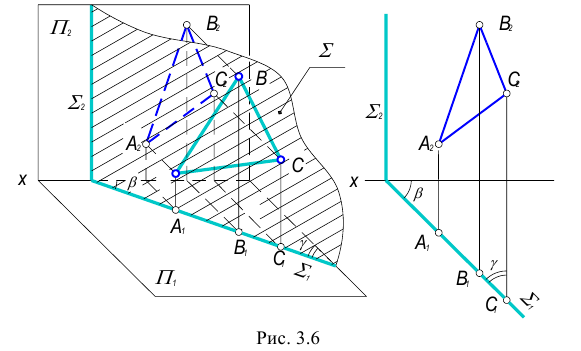
Плоскостью общего положения называется плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций.

Плоскостями частного положения относительно плоскостей проекций называются плоскости параллельные или перпендикулярные им.

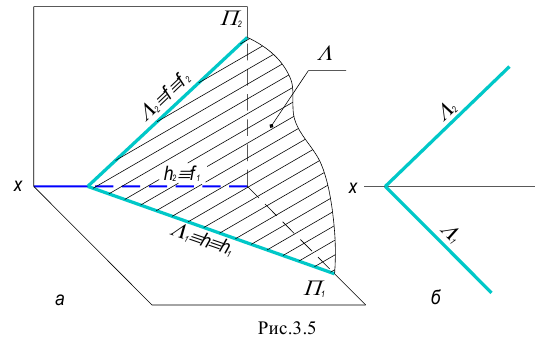
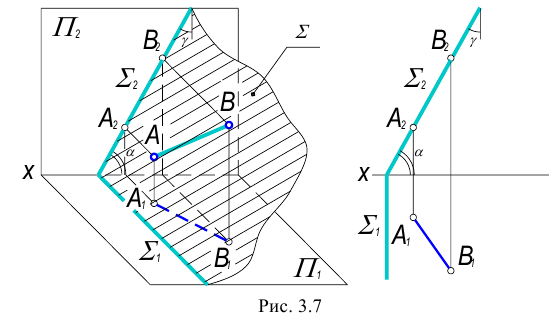
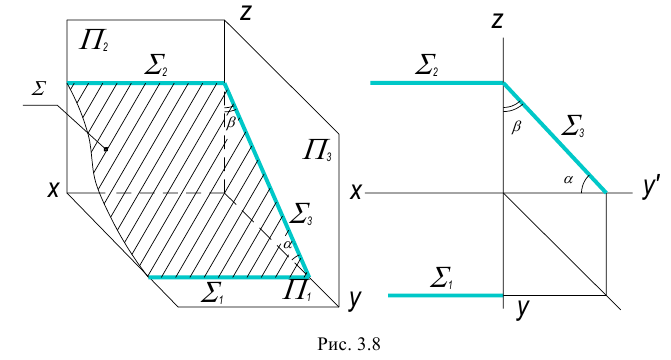
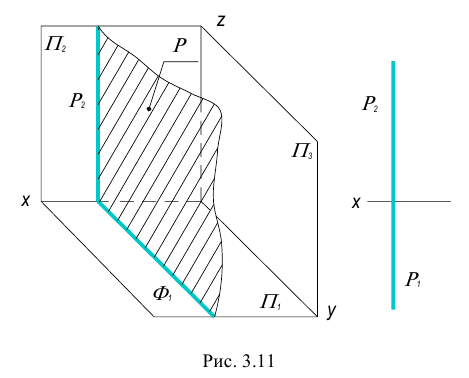
Плоскость перпендикулярная одной из плоскостей проекций называется проецирующей плоскостью.

Существует три вида проецирующих плоскостей: горизонтально- проецирующая, фронтально-проецирующая и профильно-проецирующая плоскости. Такие плоскости вырождаются в прямую линию (след плоскости) на ту плоскость проекций, к которой они перпендикулярны.

2. Фронтально-проецирующая плоскость – плоскость перпендикулярная фронтальной плоскости проекций.

3. Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

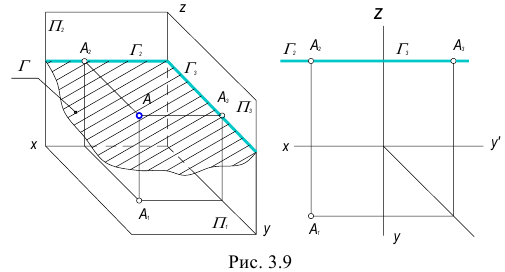
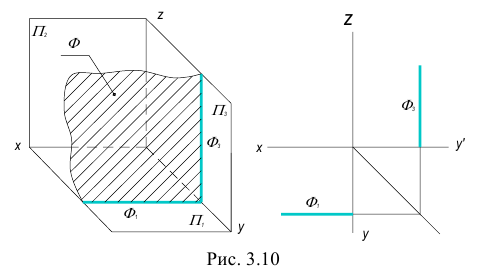
Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня.

Существует три вида плоскостей уровня: горизонтальная, фронтальная и профильная плоскости уровня.

1. Горизонтальная плоскость – плоскость, параллельная горизонтальной плоскости проекций.

3. Профильная плоскость – плоскость, параллельная профильной плоскости проекций.

Принадлежность прямой и точки плоскости

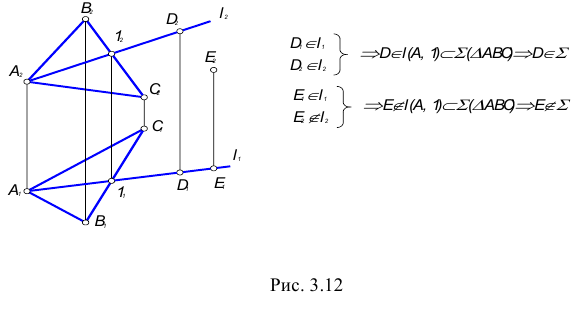
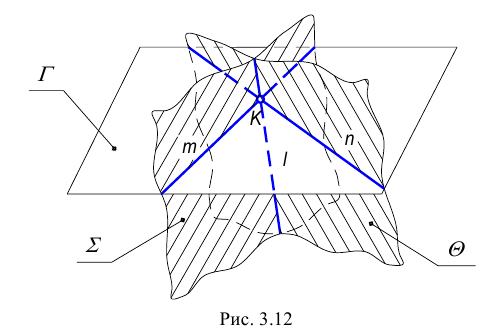
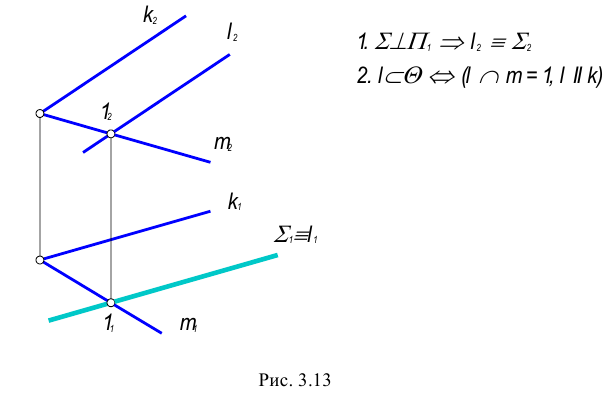
Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.12).

Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.

Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.

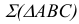
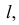
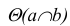
На рис. 3.12 изображена плоскость и точки D и Е. Точка D принадлежит плоскости, т. к. принадлежит прямой имеющей с этой плоскостью две общие точки – 1 и А. Точка Е не принадлежит плоскости, т.к. через нее нельзя провести прямую, лежащую в данной плоскости. На рис. 3.13. показана плоскость и прямая t, лежащая в этой плоскости, т.к. имеет с ней общую точку 1 и параллельна прямой..

Взаимное расположение прямой и плоскости

Для прямой и плоскости возможны три случая их взаимного расположения:

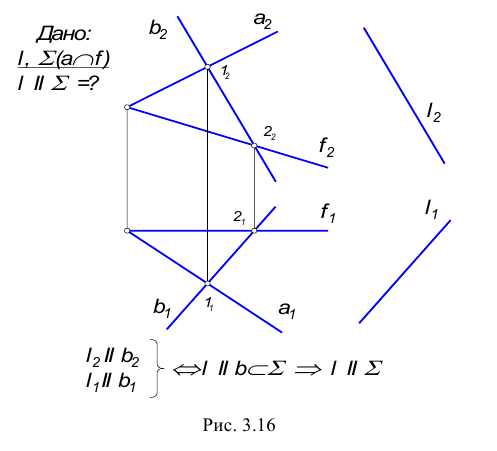
Параллельность прямой и плоскости

Прямая параллельна плоскости, если она параллельна прямой, принадлежащей этой плоскости.

Этот признак параллельности прямой и плоскости хорошо известен из курса стереометрии.

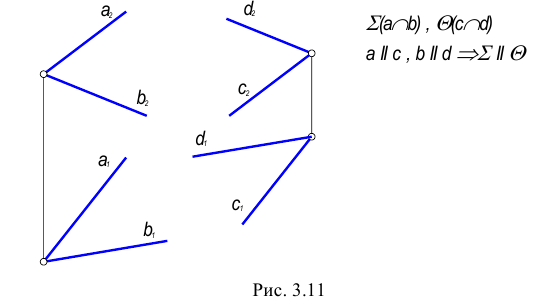
Взаимное расположение плоскостей

Плоскости по отношению друг к другу могут занимать два положения: быть параллельными или пересекаться.

Плоскости параллельны, если пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым второй плоскости

Если две плоскости не параллельны, то они обязательно пересекаются и результатом их пересечения является прямая.

Для построения линии пересечения плоскостей необходимо найти две точки, одновременно принадлежащие этим плоскостям, или одну общую точку, если известно направление линии пересечения.

Направление линии пересечения известно в том случае, если:

Общая точка для двух пересекающихся плоскостей в общем случае определяется с помощью вспомогательной плоскости частного положения, также пересекающей заданные плоскости по прямой (рис. 3.12).

Рассмотрим сначала частные случаи пересечение двух плоскостей:

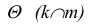
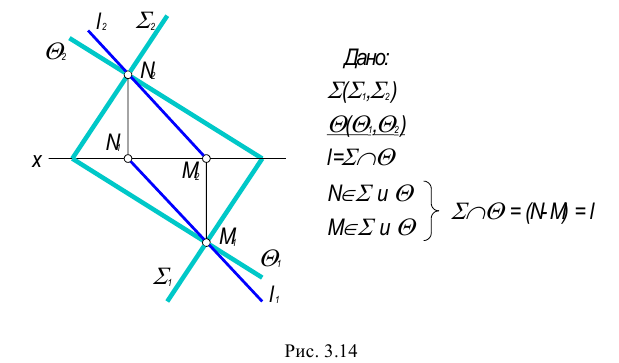
1. Пересекаются плоскость общего положения горизонтально- проецирующая плоскость заданная следом.

2. Пересекаются плоскости общего положения заданные следами.

В этом случае следы плоскости пересекаются в пределах чертежа, следовательно, линия пересечения этих плоскостей строится по двум точкам, являющимся следами линии пересечения, которые находятся в точках пересечения одноименных следов плоскостей.

Рассмотрим общий случай пересечения плоскостей:

3. Пересекаются плоскости общего положения.

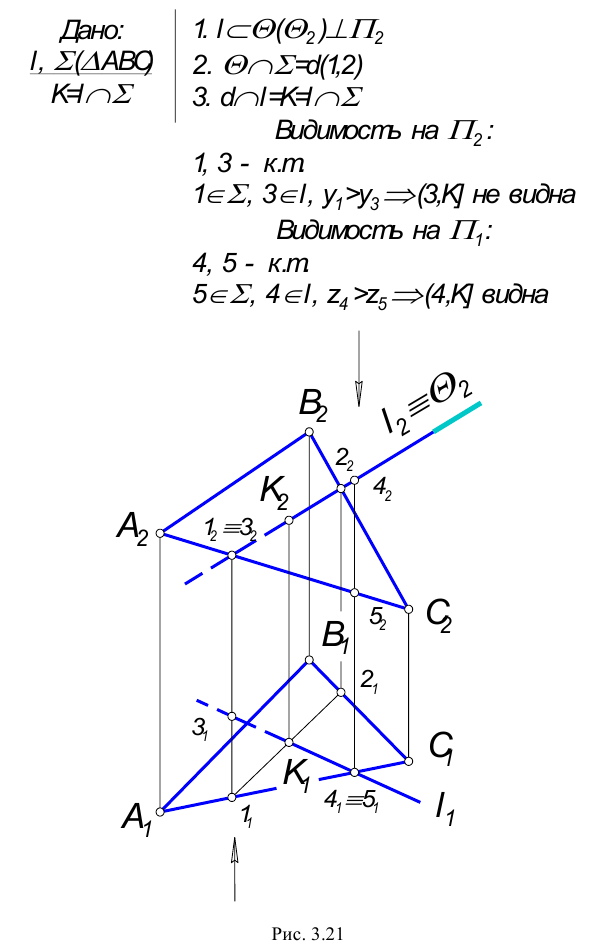
Определение видимости на КЧ

Для улучшения наглядности изображений, заданных на КЧ, принято видимые для наблюдателя линии показывать сплошными, а невидимые штриховыми линиями. При этом предполагается, что:

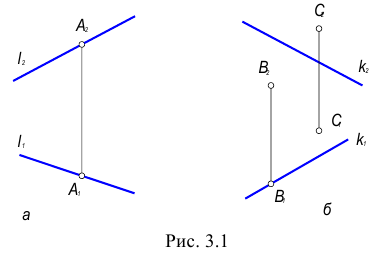
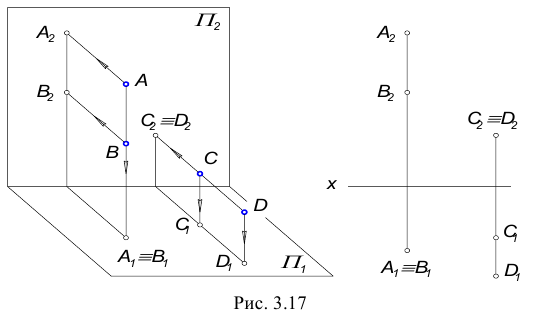
Даны две пары точек:

Необходимо определить видимость точек относительно горизонтальной и фронтальной плоскостей проекций.

Если на КЧ какие-либо две проекции точек совпадают, то для наблюдателя будет видима та точка, проекция которой на КЧ находится дальше от оси проекций.

Точки А и В, С и D называются точками, конкурирующими в видимости, а сам метод определения видимости – метод конкурирующих точек.

Конкурирующими в видимости точками называются точки, лежащие на одном проецирующем луче, но принадлежащие разным геометрическим объектам.

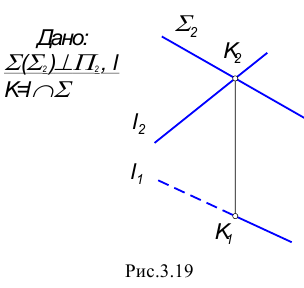
Пересечение прямой с плоскостью

Прямая называется пересекающей плоскость, если она имеет с ней только одну общую точку. Рассмотрим различные случаи пересечения прямой и плоскости,

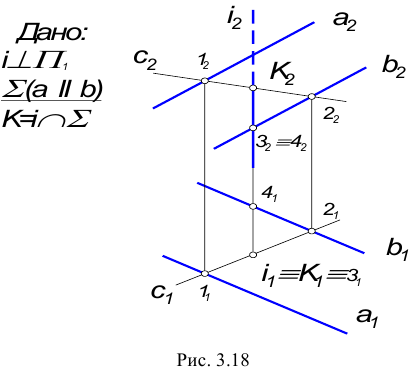
1. Прямая – проецирующая, плоскость – частного положения.

На КЧ необходимо построить проекции точки пересечения прямой с плоскостью и определить видимость этой прямой относительно горизонтальной и фронтальной плоскостей проекций. Точка К должна одновременно принадлежать и прямой, и плоскости.

В данном случае фронтальная проекция точки пересечения лежит на следе плоскости

Построение недостающей горизонтальной проекции точки пересечения сводится к задаче на принадлежность точки прямой:

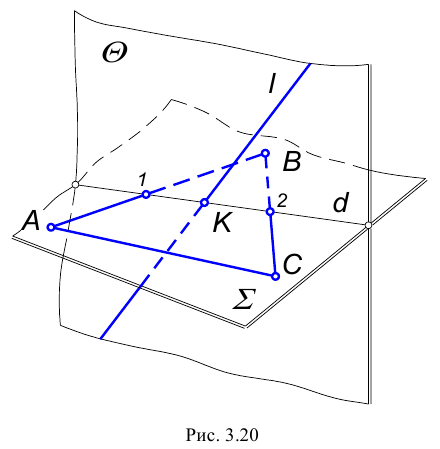
Пересечение прямой общего положения с плоскостью общего положения (первая основная позиционная задача).

В общем случае задача на пересечение прямой с плоскостью решается с помощью вспомогательной секущей плоскости, на которую накладывается ряд условий:

Порядок нахождения точки пересечения прямой с плоскостью:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Взаимное расположение прямых в пространстве. Взаимное расположение точки и прямой

Базовыми геометрическими элементами являются точка, прямая и плоскость. Они называются так потому, что из них можно построить многие объекты, например, такие как пирамида или призма. Чтобы понять свойства этих фигур, важно знать взаимное расположение в пространстве прямых и плоскостей. Рассмотрим подробнее этот вопрос в статье.

Определение и описание точки, прямой и плоскости

Вам будет интересно: Пополняем словарный запас: неказистый — это.

Вам будет интересно: «Соразмерно» — это и «в рамках», и «гармонично»

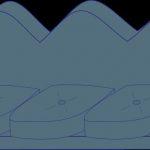
(x; y; z) = (x0; y0; z0) + α*(a; b; c)

Элементы с нулевыми индексами соответствуют некоторой точке, которая является частью прямой. Координаты, которые умножаются на параметр α (альфа) описывают ее направляющий вектор, вдоль которого она проходит. Подставляя произвольные числа α можно найти все точки, которые образуют прямую в пространстве.

Очевидно, что для векторного уравнения в двумерном пространстве необходимо использовать лишь две координаты для точек и векторов.

Плоскость является совокупностью точек. Образованные на них вектора перпендикулярны некоторому направлению, задаваемому нормальным к плоскости вектором. Все это можно описать несколькими способами. Тем не менее, для решения задач на определение взаимного расположения плоскости и прямой удобно пользоваться уравнением общего вида. Оно записано ниже:

Удобство этой формы записи заключается в том, что коэффициенты A, B, C являются координатами перпендикулярного вектора n¯ к плоскости.

При решении задач важно учитывать, в каком пространстве решается проблема. Так, приведенный вид уравнения плоскости в двумерном случае без координаты z будет соответствовать уравнению прямой.

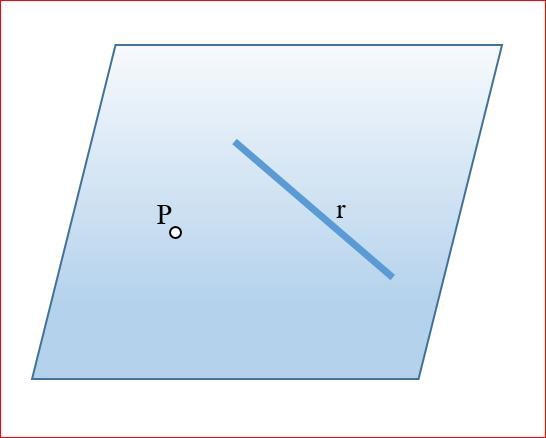
Расположение точки и прямой

Вам будет интересно: Обзор основных вузов Сургута

Взаимное расположение этих объектов не зависит от того, рассматриваются они на плоскости или в пространстве. Критерии определения постоянно одни и те же.

Относительно прямой точка может находиться лишь в двух возможных положениях:

Определить вариант расположения в конкретной задаче достаточно легко. Для этого следует подставить координаты искомого объекта в уравнение, задающее прямую. Если равенство будет выполняться, значит, точка принадлежит прямой. В противном случае она не является ее частью.

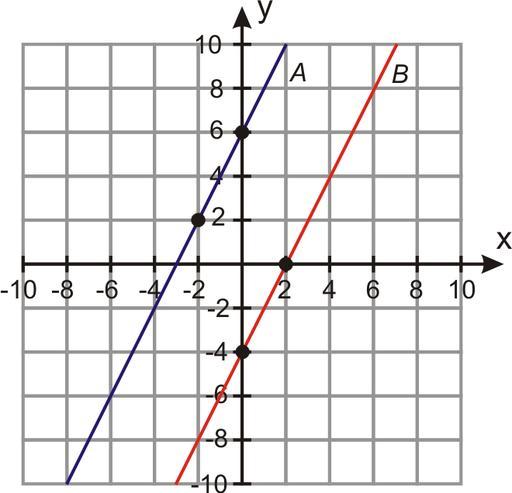
Две прямые на плоскости

Какое может быть взаимное расположение двух прямых на плоскости? Существует три разных варианта:

Чтобы понять, каково взаимное расположение прямых в конкретном случае, необходимо провести некоторый математический анализ. Ниже описываются основные идеи, которые следует использовать при его осуществлении.

Если направляющие векторы прямых параллельны друг другу, значит и прямые, как минимум, будут параллельными. Параллельность векторов доказывается, если один из них можно представить в виде другого, умноженного на действительное число.

Если направляющие вектора параллельны, и хотя бы одна точка одной прямой соответствует и другой прямой, тогда речь идет о полностью совпадающих прямых.

Если направляющие вектора не являются параллельными, то прямые пересекаются в одной точке. Найти ее координаты можно с помощью решения системы уравнений (эти координаты должны соответствовать обоим уравнениям прямых).

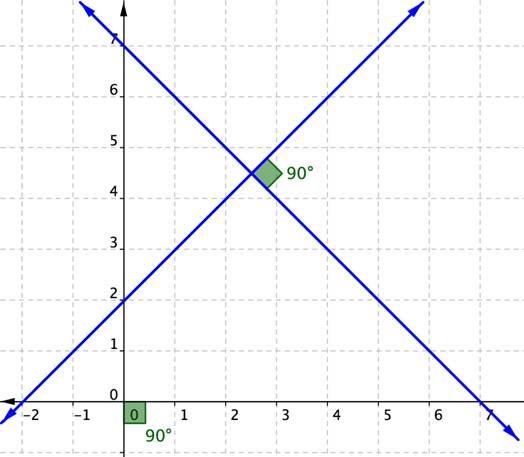
Частным случаем пересечения прямых является угол пересечения, равный 90o. В таком случае говорят о перпендикулярности между рассматриваемыми объектами. Если две прямые перпендикулярны, то скалярное произведение их векторов направляющих будет равно нулю.

Прямая и окружность на плоскости

Поскольку данный объект часто появляется в геометрических задачах, то полезно также рассмотреть вопрос взаимного расположения окружности и прямой. Возможны такие варианты:

Определить вариант расположения этих объектов для конкретной задачи можно с использованием соответствующих уравнений. Для окружности с центром в (x0; y0) и радиусом R оно имеет вид:

Определение варианта расположения сводится к решению квадратного уравнения.

Две прямые в пространстве

Расчет расстояния производится по формуле:

Формулу можно непосредственно применить, если даны векторные уравнения прямых.

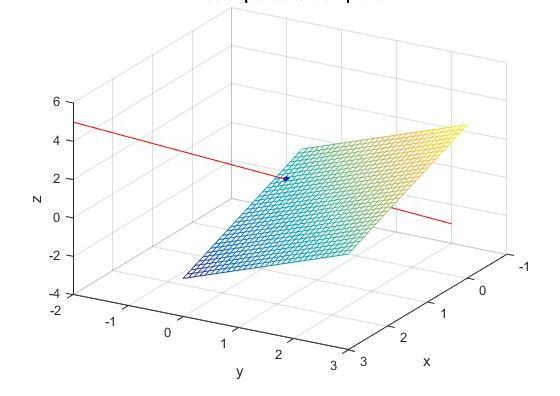
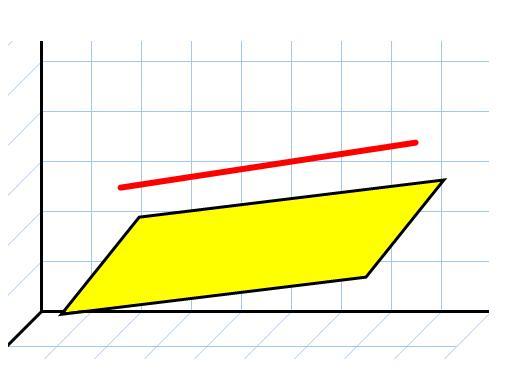
Плоскость и прямая

В данном случае речь идет о трехмерном пространстве. Взаимное расположение плоскости и прямой возможно следующее:

Определить параллельность этих геометрических объектов достаточно просто. Для этого нужно рассчитать скалярное произведение нормального вектора плоскости и направляющего вектора прямой. Равенство нулю этого произведения является достаточным условием параллельности. Если к тому же хотя бы одна точка принадлежит плоскости, значит, вся прямая лежит в ней.

Если скалярное произведение нулю не равно, тогда вывод следующий. Прямая и плоскость пересекаются в одной точке. Частным случаем является пересечение под прямым углом. Если направляющий вектор прямой можно представить в виде произведения на число вектора нормали к плоскости, значит, прямая и плоскость перпендикулярны.

Задача с двумя прямыми на плоскости

Ниже даны два уравнения в общем виде для прямых в двумерном пространстве:

Необходимо определить взаимное расположение прямых.

Поскольку имеет место случай на плоскости, то нет необходимости приводить эти уравнения к векторному виду. Решить задачу можно проще, если найти корни системы из этих них. Имеем:

Поскольку система имеет единственное решение, то оно соответствует пересечению рассматриваемых прямых в точке (14; 21).

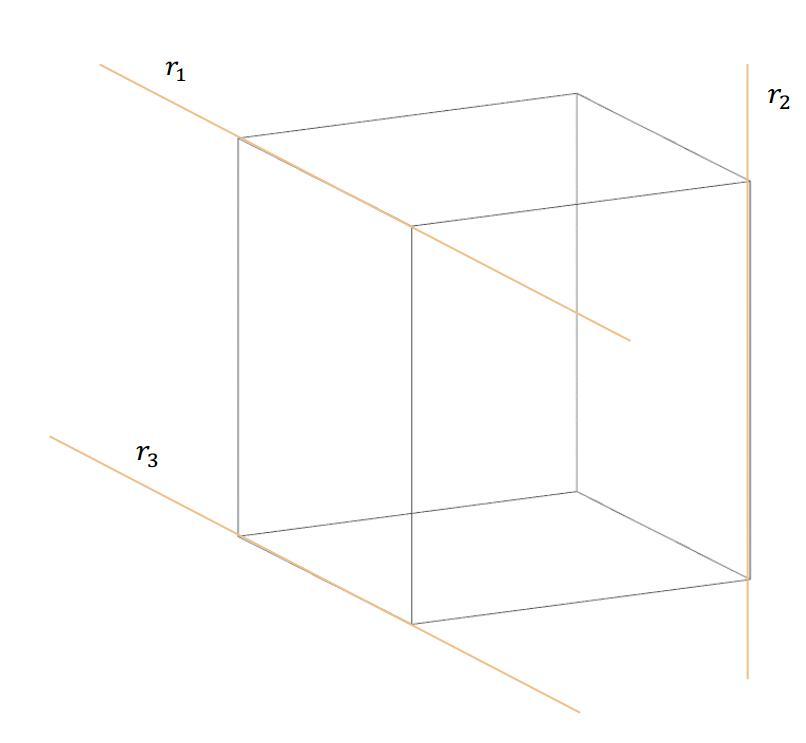
Задача с двумя прямыми в пространстве

Даны две прямые, которые описываются уравнениями:

Каково взаимное расположение прямых в пространстве?

Можно заметить, что направляющие вектора параллельными не являются (никакое значение параметра β не способно дать направляющий вектор r1). То есть прямые либо пересекаются, либо являются скрещивающимися.

Его векторное произведение с направляющим вектором для r1 равно:

Поскольку длина этого вектора отлична от нуля, значит, расстояние между прямыми будет больше нуля. Последний факт говорит, что они не имеют общих точек и являются скрещивающимися.

Источник