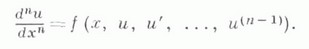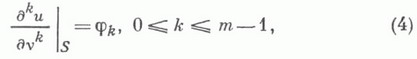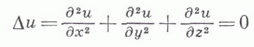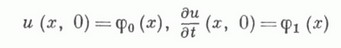В чем заключается задача коши
Коши задача
Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).
От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.
Основные вопросы, которые связаны с задачей Коши, таковы:
Содержание
Различные постановки задачи Коши
Свойства задачи Коши
См. также
Литература
А.Н. Тихонов, А.Б. Васильева, А.Г. Свешников Курс высшей математики и математической физики. Дифференциальные уравнения. — Физматлит, 2005. — ISBN 5-9221-0277-X
Полезное
Смотреть что такое «Коши задача» в других словарях:
Коши задача — одна из основных задач теории дифференциальных уравнениний. Заключается в нахождении решения такого уравнения, удовлетворяющего так называемым начальным условиям. Например, для уравнения dy = 2xdx можно поставить Коши задачу: найти решение… … Энциклопедический словарь
КОШИ ЗАДАЧА — задача о нахождении решения дифференц. ур ния (обыкновенного или в частных производных), удовлетворяющего нач. условиям. Рассмотрена в 1823 24 О. Коши (A. Cauchy). Примером К. з. может служить осн. задача механики, когда по известным нач.… … Физическая энциклопедия
КОШИ ЗАДАЧА — одна из основных задач теории дифференциальных уравнений. Заключается в нахождении решения такого уравнения, удовлетворяющего т. н. начальным условиям. Напр., для уравнения dy = 2xdx можно поставить Коши задачу: найти решение у = у(х),… … Большой Энциклопедический словарь
КОШИ ЗАДАЧА — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в отыскании решения (интеграла) дифференциального уравнения, удовлетворяющего так наз. начальным условиям (начальным данным). К. з. обычно… … Математическая энциклопедия
Коши задача — одна из основных задач теории дифференциальных уравнений (См. Дифференциальные уравнения), впервые систематически изучавшаяся О. Коши. Заключается в нахождении решения u (x, t); х = (x1. xn) дифференциального уравнения вида: … … Большая советская энциклопедия
КОШИ ЗАДАЧА — численные методы решения для обыкновенного дифференциального уравнения. Задачей Коши наз. задача определения функции или нескольких функций, удовлетворяющих одному или, соответственно, системе дифференциальных уравнений и принимающих заданные… … Математическая энциклопедия
КОШИ ЗАДАЧА — одна из оси. задач теории дифференц. ур ний. Заключается в нахождении решения такого ур ния, удовлетворяющего т. н.начальным условиям. Напр., для ур ния dy = 2xdx можно поставить К. з.: найти решение у = у(х), принимающее при х0 = 0 значение… … Естествознание. Энциклопедический словарь
КОШИ ХАРАКТЕРИСТИЧЕСКАЯ ЗАДАЧА — задача отыскания решения дифференциальных уравнений или систем уравнений с частными производными по заданным его значениям на характеристических многообразиях. Для широкого класса уравнений гиперболического и параболического типов в пространстве… … Математическая энциклопедия
Коши — (Cauchy) Огюстен Луи (21.8.1789, Париж, 23.5.1857, Со), французский математик, член Парижской АН (1816). Окончил Политехническую школу (1807) и Школу мостов и дорог (1810) в Париже. В 1810 13 работал инженером в г. Шербур. В 1816 30… … Большая советская энциклопедия
Инструменты пользователя
Инструменты сайта
Боковая панель
Теория вероятностей и математическая статистика 
Строительная механика для строительных специальностей
Матанализ. Дифференциальное и интегральное исчисление
Экономика
Решение дифференциальных уравнений:
Контакты
Решение задачи Коши (диффуры)
Задача Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).
Что бы решить задачу Коши – нужно получить общее решение дифференциального уравнения в которое входят произвольные постоянные, количество которых зависит от порядка дифференциального уравнения и численно равно этому порядку. Собственно, решение задачи Коши и отличается от нахождения общего решения дифференциального уравнения тем, что, используя общее решение с учётом начальных условий находят эти произвольные константы, входящие в общее решение.
От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.
Примеры
Пример 1.
Решение дифференциального уравнения:
Дифференциальные уравнения с разделяющимися переменными. Решение задачи Коши
КОШИ ЗАДАЧА
— одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в отыскании решения (интеграла) дифференциального уравнения, удовлетворяющего так наз. начальным условиям (начальным данным). К. з. обычно возникает при анализе процессов, определяемых дифференциальным законом и начальным состоянием, математич. выражением к-рых и являются уравнение и начальное условие (откуда терминология и выбор обозначений: начальные данные задаются при (=0, а решение отыскивается при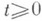 
). От краевых задач К. з. отличается тем, что область, в к-рой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее и К. з. можно рассматривать как одну из краевых задач.
Основные вопросы, к-рые связаны с К. з., таковы.
1) Существует ли (хотя бы локально) решение К. з.?
2) Если решение существует, то какому пространству оно принадлежит, в частности, какова область его существования?
3) Является ли решение единственным?
4) Если решение единственно, то будет ли оно корректным, т. е. непрерывным (в каком-либо смысле) относительно начальных данных?
Простейшая К. з. состоит в том, что требуется найти определенную на полупрямой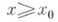 
функцию и(х), к-рая удовлетворяет обыкновенному дифференциальному уравнению 1-го порядка
Дословно так же формулируется К. з. для систем обыкновенных дифференциальных уравнений, т. е. для обыкновенного дифференциального уравнения вида (1) с начальным условием (2), где и=и (х).- функция со значением в конечномерном векторном пространстве
— функция, определенная в 
Для существования, единственности и корректности решения К. з. и здесь достаточны условия Пикара.
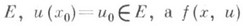
Для обыкновенных дифференциальных уравнений высших порядков
К. з ., в начальных данных к-рой участвуют, помимо самой функции, и ее производные
стандартным приемом сводится к соответствующей задаче вида (1), (2).
В случае обыкновенных дифференциальных уравнений 1-го порядка, не разрешимых относительно производной искомой функции, постановка К. з.- та же, разве что в большей степени опирается на ее геометрич. трактовку, но исследование может осложняться невозможностью (даже локальной) редукции уравнения к нормальной форме (1).
состоящей в отыскании ( п-k )-мерной интегральной поверхности, проходящей через данную точку, имеет вид
(в окрестности этой точки; здесь d,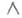
— символы внешнего дифференциала и внешнего произведения соответственно) (см. Фробениуса теорема).
Для линейных дифференциальных уравнений с частными производными
В этом случае вблизи точки х 0 уравнений (3) можно записать в так наз. нормальной форме
К. з. обычно рассматривается, когда носителем начальных данных является характеристич. поверхность, т. е. когда условие (5) выполнено для всех 
с начальными условиями
не имеет решения, если функция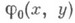 
не является аналитической.
Широкий класс уравнений, для к-рых К. з. поставлена корректно, составляют гиперболич. уравнения. В этом случае К. з. носит глобальный характер, однако условия нехарактеристичности Sпри этом недостаточно. Необходимо, чтобы Sбыла поверхностью пространственного типа. Модельным уравнением гиперболич. типа является волновое уравнение
на гиперплоскости t=0 однозначно разрешима для любых достаточно гладких функций 
и решение непрерывно зависит в метрике пространств C k от этих функций. Для случаев n=1, n=2 и n=3 явный вид этого решения дается формулами Д’А л а м б е р а, Пуассона и Кирхгофа соответственно:
где 
— элемент поверхности единичной сферы 
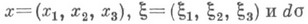
Множество точек на плоскости t=0, данные Коши на к-ром вполне определяют значение и( х, t).решения волнового уравнения (7) в точке ( х, t), наз. областью зависимости для этой точки. Областями зависимости точки ( х, t).в случаях n=1, n=2 и n=3 являются отрезок, круг и шар, определяемые соотношением 
(в соответствующем пространстве R n ). Если носителем данных Коши является нек-рая область Sгиперплоскости t=0, то данные Коши в этой области влияют на решение во всех точках ( х, t).множества, для к-рого пересечение 
не пусто; это множество наз. областью влияния.
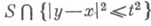
Множество точек 
, на к-ром решение ивполне определяется по данным Коши на S, наз. областью определения и( х, t) с начальными данными на S. В случае n=1, n=2 и n=3 область определения образуют все точки ( х, t), для к-рых отрезок, круг и шар 
соответственно расположены в S.
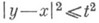
Эти результаты распространяются на более общий случай, когда носителем данных Коши является: поверхность Sпространственного типа, то есть поверхность, для к-рой величина Qв (5) сохраняет на Sположительное значение.
Для вырождающихся уравнений К. з. имеет свои особенности. Напр., если уравнение гиперболич. типа и носителем данных Коши является поверхность, на к-рой уравнение параболически вырождается, то в зависимости от характера вырождения принятие начальных условий может осуществляться с нек-рым весом.
Лит.:[1] К о в а л е в с к а я С. В., Научные работы, М., 1948; [2] А д а м а р Ж., Задача Коши для линейных уравнений с частными производными гиперболического типа, пер. с франц., М., 1978; [3] Берс Л., Джон Ф.,Шехтер М., Уравнения с частными производными, пер. с англ., М., 1966; [4] Б и ц а д з е А. В., Уравнения математической физики, М., 1976; [5] Курант Р., Уравнения с частными производными, иер. с англ., М., 1964; [6] Мизохата С., Теория уравнений с частными производными, пер. с япон., М., 1977; [7] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972; [8] Хёрмандер Д., Линейные дифференциальные операторы с частными производными, пер. с англ., М., 1965. А. П. Солдатов.
Принцип и понятие
Под задачей Коши для дифференциального уравнения понимают выражение вида: y’ = f (x, y) с начальным условием, соответствующим равенству: y (x0) = y0. По сути, это обозначает, что необходимо найти такое решение уравнения, которое проходит через заданную точку игрек и икс нулевое. Решением задачи называется функция, заданная на указанном интервале в окрестности точки икс нулевое, то есть: x Є (x0 — q, x0 + q).
Для проведения анализа функции должны выполняться следующие критерии:
Следует отметить, что решение Коши включает в себя и сам интервал икс нулевое плюс минус кью, фактически q-окрестность. Это обозначает, что одна и та же функция, задаваемая одной формулой, но рассматриваемая на разных интервалах, представляет два разных нахождения задачи Коши. Отсюда возникает вопрос, при каких же ответах существует решение Коши, а также когда оно будет единственным.
Существует теорема, гарантирующая единственность какого-то решения задачи. На самом деле возможность аналитического подхода Коши требует лишь главного условия, при котором функция f будет непрерывной в какой-то окрестности точки x0, y0. Но для доказательства единственности этого недостаточно. Для нормального случая необходимо следующее:
По игреку функция должна иметь обыкновенный рост, то есть не убыстряющийся (локальный подъём не превышать линейный). Если эти два условия выполняются, то решение Коши существует и оно будет единственным. Это значит, что тогда у точки икс нулевое найдётся такая окрестность, в которой существует решение и к тому же оно будет единственным.
А это обозначает, что любая другая функция в этой окрестности, удовлетворяющая уравнениям начальных условий, совпадает с той, существование которой утверждается. При этом на практике проверка условия на самом деле вещь не очень сложная, особенно если функция f (y) имеет в окрестности ограниченную производную.
Алгоритм нахождения
Пусть имеется функция у’ = 2 * √ |y| и условие что y (0) = 0. Необходимо её исследовать. Тут можно заметить, что в этом случае функция зависит только от игрека и условию не удовлетворяет. В окрестностях точки с координатами (0, 0) она не удовлетворяет условию, так как любая окрестность захватывает ноль, а у корня квадратного по игреку будет бесконечная производная.
Это приводит не к единственности получения результатов. Так, у уравнения есть два решения: y1 тождественный нулю; y2 равняется x2. Согласно условию, игрек стоит по модулю, точнее, можно сказать, что для отрицательных значений икс будет меньше ноля, а положительных — больше.
Главный же вопрос заключается в продолжаемости анализа. Доказывается возможность простым построением решения с использованием специальных условий. В итоге должна быть найдена окрестность в точке x0. То есть берётся уравнение и точка с начальными координатами, затем выясняется, что в окрестности выполнены условия теоремы и строится решение.
Затем исследуется другая точка и изучается структура её окрестности. Например, обнаруживается, что условия существования единственности выполняются. Согласно теореме, тогда можно будет строить решение, где в качестве начальной точки будет взята любая координата. Другими словами, получается более широкое решение. Поэтому возникает вопрос, насколько можно приблизить точность ответа. Практические примеры показывают, что иногда можно двигаться до бесконечности, а в некоторых случаях сделать не более трёх шагов.
Если есть два уравнения y’ = f (x, y); y (x0) = y0 имеющие два решения: y1 (x), x Є I1 (эX), y2 (x), x єI2 (єX0). Тогда можно утверждать, что игрек два будет продолжением решения y1 (x) если в I2 входит I1, а y2 (x) равняется y1 (x) для любого икс из интервала I1. Следует учесть, что в этом определении в качестве областей функции всегда рассматривается интервал.
В изучении исследуются и матричные функциональные системы, состоящие из нескольких переменных A (z 1, z 2, …, zn). При этом z являются вещественными, а элементы матрицы могут быть как вещественными, так и комплексными. Исходя из этого даётся определение того, что функция, описываемая матрицей, непрерывна тогда, когда все элементы непрерывны в точке или на некотором множестве.
При определении используют численные и векторные функции от аргумента: y = (x), где y — это столбец от набора игреков, а икс со штрихом — от набора иксов. Таким образом, обобщённым решением будет такое действие, которое не будет иметь нетривиального продолжения, то есть вторые интервалы содержать первые.
Примеры задач
На практических занятиях по высшей математике студентам предлагается для понимания курса выполнить ряд практических заданий. Существует типовой набор задач, научившись решать которые учащийся досконально разберётся в теме. Вот некоторые из них.
Первый пример. Имеется уравнение y’ = (2y / x lnx) + 1/x, для которого установлено начальное условие y (e) = 0. Необходимо найти решение, проходящее через точку e. Перед тем как приступить непосредственно к решению, необходимо отметить, что функция f (x, y) определённа всюду, за исключением прямых x = 0 и x = 1. Отсюда следует, что краевое решение не может быть вычислено на интервале от нуля до единицы.
В этом примере должен содержаться интервал, имеющий координату точки e по иксу. Он не может включать значения меньше единицы, так как необходимо, чтобы выполнялось заданное условием уравнение, которое в точке x = 1 теряет смысл, ведь в ней функция неопределённа. Установив это, можно переходить к анализу уравнения.
Заданное равенство является линейным — неоднородным уравнением первого порядка. Для решения нужно сначала рассмотреть левое соотношение: y’ = 2y / x * lnx. Добавив константу, уравнение можно переписать как y = c * e. Теперь необходимо взять интеграл исходя из первообразной формулы: ∫ 2 dx / (x *lnx).
После того как будет найдена постоянная, через общий интегральный метод с учётом условия определения функции, уравнение в окрестности точки e будет иметь решение вида: y = ln2x — lnx. Из полученного выражения можно сделать вывод, что функция будет определена для всех положительных иксов, но рассматривать её необходимо от единицы до плюс бесконечности. Это и будет максимальное непродолжаемое решение задачи: xЄ (1, + ∞).
Второй пример. Пусть имеется функция y’ = y / (1+x 2 ) с начальным условием: y = y (0). В задании нужно будет рассмотреть дифференциальную кривую уравнения, проходящего через точку y0. Нужно заметить, что функция f (x, y) в любой ограниченной области двумерной плоскости удовлетворяет условию регулярности для теоремы существования единственности. В задаче спрашивается, каким должен быть y0, если предел максимального решения при иксе, стремящемся к плюс бесконечности, равняется единице.
Операционный метод
Решение задачи Коши (примеров) целесообразно выполнять экономичным методом интегрирования линейных выражений, содержащих постоянные коэффициенты. Суть способа сводится к решению алгебраических равенств или неравенств. Алгоритм исследования заключается в следующих действиях:
Использование онлайн-калькулятора
Часто решение задач по рассматриваемой теме связано с большими трудозатратами. Это касается времени и повышенного внимания. На практике не всегда получается правильно применить алгоритм и избежать ошибок. Поэтому имеет смысл для сложных заданий использовать онлайн-калькулятор. Решения на задачу Коши с его помощью доступны любому заинтересованному, имеющему доступ к интернету и устройство, поддерживающее работу веб-обозревателя.
В интернете существует довольно большое количество различных математических онлайн-решителей. В своём большинстве они бесплатны и ориентированы на работу даже с людьми, совершенно не разбирающимися в тематике. Поэтому они привлекательны не только как инструмент, предоставляющий быстрый и правильный ответ на поставленную задачу, но и как обучающие программы.
Всё дело в том, что на страницах сервисов, предлагающих такого рода услуги, содержится вся необходимая теоретическая информация. Кроме этого, они предлагают к рассмотрению типовые примеры с подробным объяснением решения. Из онлайн-калькуляторов, предоставляющих бесплатный доступ к своим услугам в русском сегменте интернета, можно отметить следующие:
Приведённые сервисы помогают без труда найти студентам решение дифференциального уравнения с заданными начальными условиями. Для этого в предлагаемую форму необходимо записать дифуравнение и через запятую начальные данные. Затем просто нажать интерактивную кнопку «Решить» и через некоторое время на экране дисплея отобразится ответ.
Для правильной записи уравнения существуют подсказки, так что разобраться, как работает сайт, сможет пользователь даже со слабой компьютерной подготовкой. Кроме этого, некоторые сервисы предлагают не просто ответ, а и пошаговое решение, к которому даётся комментарий. Решив несколько заданий, учащийся сможет разобраться в алгоритме и вычислять уравнения уже самостоятельно.
Следует отметить, что предложенные сервисы могут находить ответ для любой сложности математической задачи, например, вычисляя устойчивость математических моделей. Они также востребованы в инженерии и научных исследованиях, связанных с анализом функций. Для таких расчётов важны точность и время, что вполне могут обеспечить математические онлайн-сервисы.