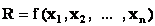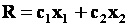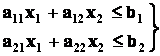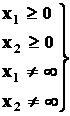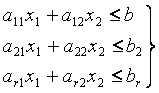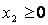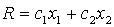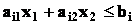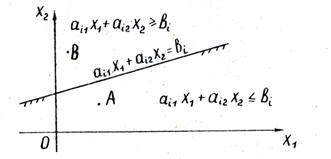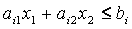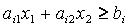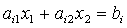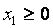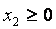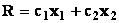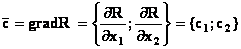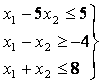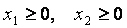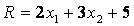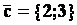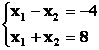В чем заключается задача оптимизации

Задача оптимизации

Задачей оптимизации в математике называется задача о нахождении экстремума (минимума или максимума) вещественной функции в некоторой области. Как правило, рассматриваются области, принадлежащие и заданные набором равенств и неравенств.

Содержание

Постановка задачи оптимизации

Для того, чтобы корректно поставить задачу оптимизации необходимо задать:

Тогда решить задачу 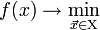означает одно из:

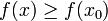
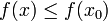
Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек x₀ таких, что всюду в некоторой их окрестности для минимума и для максимума.

Если допустимое множество 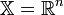, то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

Классификация методов оптимизации

Методы, по средством которых решают задачи оптимизации, подразделяются на виды, соответствующие задачам, к которым они применяются:

Существующие в настоящее время методы поиска можно разбить на три большие группы:

Некоторые детерминированные методы:

Помимо того, оптимизационные методы делятся на следующие группы:

Также они разделяются по критерию размерности допустимого множества на методы одномерной оптимизации и методы многомерной оптимизации.

Литература

Ссылки

Методы второго порядка:
(требуют значения первой и второй частных производных):
Метод Ньютона • Метод Ньютона-Рафсона

Полезное

Смотреть что такое «Задача оптимизации» в других словарях:

задача оптимизации надёжности — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN reliability optimization problem … Справочник технического переводчика

Задача о порядке перемножения матриц — Задача о порядке перемножения матриц классическая задача динамического программирования, в которой дана последовательность матриц и требуется минимизировать количество скалярных операций для вычисления их произведения. Матрицы… … Википедия

Задача о рюкзаке — Задача о ранце (рюкзаке) одна из задач комбинаторной оптимизации. Название это получила от максимизационной задачи укладки как можно большего числа нужных вещей в рюкзак при условии, что общий объём (или вес) всех предметов ограничен. Подобные… … Википедия

Задача о рюказаке — Задача о ранце (рюкзаке) одна из задач комбинаторной оптимизации. Название это получила от максимизационной задачи укладки как можно большего числа нужных вещей в рюкзак при условии, что общий объём (или вес) всех предметов ограничен. Подобные… … Википедия

Задача о коммивояжере — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия

Задача о коммивояжёре — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия

Задача коммивояжера — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия

Задача коммивояжёра — Оптимальный маршрут коммивояжёра через 15 крупнейших городов Германии. Указанный маршрут является самым коротким из всех возможных 43 589 145 600. Задача коммивояжёра (англ. Travelling salesman problem, TSP) (коммивояжёр&#16 … Википедия

Задача о ранце — Пример задачи о ранце: необходимо разместить ящики в рюкзак при условии на вместимость рюкзака 15 кг, так чтобы суммарная полезность предметов в рюкзаке была максимальной. Задача о ранце (рюкзаке) (англ. … Википедия

Задача о максимальном потоке — Максимальный поток в транспортной сети. Числа обозначают потоки и пропускные способности. В теории оптимизации и теории графов, задача о максимальном потоке заключается в нахождении такого потока по транспортной сети, что сум … Википедия

Источник

В чем заключается задача оптимизации

5. Многомерная оптимизация

Оптимизация – это целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.

Количественная оценка оптимизируемого качества называется критерием оптимальности или целевой функцией. Её можно записать в виде:

Существуют два типа задач оптимизации – безусловные и условные.

Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной функции (5.1) от n действительных переменных и определении соответствующих значений аргументов.

Решение задач оптимизации, в которых критерий оптимальности является линейной функцией независимых переменных (то есть содержит эти переменные в первой степени) с линейными ограничениями на них, составляет предмет линейного программирования.

Слово «программирование» отражает здесь конечную цель исследования – определение оптимального плана или оптимальной программы, по которой из множества возможных вариантов исследуемого процесса выбирают по какому-либо признаку наилучший, оптимальный, вариант.

Примером такой задачи является задача оптимального распределения сырья между различными производствами при максимальной стоимости продукции.

Пусть из двух видов сырья изготавливается продукция двух видов.

Учитывая, что расход данного ресурса не может превышать общего его количества, запишем ограничительные условия по ресурсам:

В аналогичном виде формулируются так называемые транспортные задачи (задачи оптимальной организации доставки товаров, сырья или продукции из различных складов к нескольким пунктам назначения при минимуме затрат на перевозку) и ряд других.

Графический метод решения задачи линейного программирования.

и условиям неотрицательности :

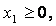
для которых функция

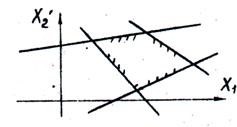
Построим в системе прямоугольных координат x ₁ Ox ₂ область допустимых решений задачи (рис.11). Для этого, заменяя каждое из неравенств (5.5) равенством, строим соответствующую ему граничную прямую:

а для координат любой точки В другой полуплоскости – противоположное неравенство:

Координаты любой точки граничной прямой удовлетворяют уравнению:

Для определения того, по какую сторону от граничной прямой располагается полуплоскость, соответствующая заданному неравенству, достаточно «испытать» одну какую-либо точку (проще всего точку О (0;0)). Если при подстановке её координат в левую часть неравенства оно удовлетворяется, то полуплоскость обращена в сторону к испытуемой точке, если же неравенство не удовлетворяется, то соответствующая полуплоскость обращена в противоположную сторону. Направление полуплоскости показывается на чертеже штриховкой. Неравенствам:

соответствуют полуплоскости, расположенные справа от оси ординат и над осью абсцисс.

На рисунке строим граничные прямые и полуплоскости, соответствующие всем неравенствам.

Общая, часть (пересечение) всех этих полуплоскостей будет представлять собой область допустимых решений данной задачи.

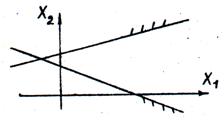
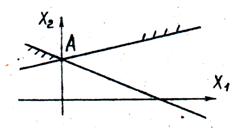
При построении области допустимых решений в зависимости от конкретного вида системы ограничений (неравенств) на переменные может встретиться один из следующих четырех случаев:

Рис. 12. Область допустимых решений пустая, что соответствует несовместности системы неравенств; решения нет

Рис. 14. Область допустимых решений ограниченная, изображается в виде выпуклого многоугольника. Допустимых решений бесконечное множество

Рис. 15. Область допустимых решений неограниченная, в виде выпуклой многоугольной области. Допустимых решений бесконечное множество

Графическое изображение целевой функции

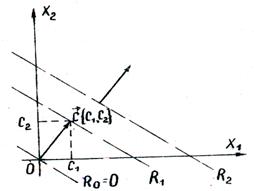
Задача отыскания оптимального решения системы неравенств (5.5), для которого целевая функция R (5.7) достигает максимума, гео­метрически сводится к определе­нию в области допустимых реше­ний точки, через которую пройдет линия уровня, соответствую­щая наибольшему значении пара­метра R

Если область допустимых решений есть выпуклый многоугольник, то экстремум функции R достигается, по крайней мере, в одной из вер­шин этого многоугольника.

Если экстремальное значение R достигается в двух вершинах, то такое же экстремальное значение достигается в любой точке на отрезке, соединяющем эти две вершины. В этом случае говорят, что задача имеет альтернативный оптимум.

В случае неограниченной области экстремум функции R либо не существует, либо достигается в одной из вершин области, либо имеет альтернативный оптимум.

и условиям неотрицательности :

для которых функция:

Заменим каждое из неравенств равенством и построим граничные прямые:

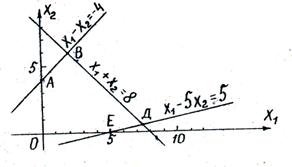
Определим полуплоскости, соответствующие данным неравенствам, путём «испытания» точки (0;0). С учетом неотрицательности x ₁ и x ₂ получим область допустимых решений данной задачи в виде выпуклого многоугольника ОАВДЕ.

В области допустимых решений находим оптимальное решение, строя вектор градиента

Задания. Найти положение точки экстремума и экстремальное значение целевой функции

Источник

Прикладная практика оптимизации и немного истории

В патентовании есть такая категория изобретений, когда патентуется не то, что человек/коллектив придумал (оно уже достаточно давно известно, например, клей), и не новый способ достижения актуальной цели (например, герметизация раны от инфекции). А патентуется, например, применение широко известного вещества в совершенно новом (для данного вещества), но тоже хорошо и давно известном для достижения цели применении. «А давайте попробуем заклеить рану клеем БФ-6? О! А он, оказывается, имеет бактерицидные свойства. и рана под ним дышит. и быстрее заживает! Надо застолбить и применять!»

В прикладной математике есть инструменты, грамотное применение которых позволяет решать оч-ч-чень большой круг самых различных задач. Об этом я и хочу вам рассказать. Может кого натолкну на поиски своего нетривиального применения успешно освоенных алгоритмов или приёмов/программ. Здесь будет мало отсылок на строгие математические инструменты или соотношения, больше качественный разбор преимуществ и приложений численного метода (методов), сыгравшего в моей жизни большую роль и ставшего основой решения важных профессиональных задач.

Довольно давно (при защите диссертации и работе на военно-космическом предприятии, Краснодар) был разработан инструментарий для решения задач оптимизации — поиска локального экстремума многопараметрической функции на некотором множестве ограничений для её параметров. Такие методы широко известны, например, почти все знакомы с методом наискорейшего спуска (Градиентный спуск).

Комплекс программ (сначала Fortran, потом Pascal/Modula 2, ныне алгоритм упокоился в хорошо наследуемом, удобном и универсальном VBA/Excel) реализовывал несколько различных известных методов поиска экстремума, которые удачно дополняли друг друга на очень широком классе задач. Они были легко взаимозаменяемы и, установленные в стек (следующий стартовал с оптимума, найденного предыдущим, с широким охватом возможных начальных значений параметров), достаточно быстро находили минимум и «дожимали» целевую функцию с хорошей гарантией глобальности найденного экстремума.
Например, с применением этого комплекса программ была построена модель автономной системы, состоящей из солнечных батарей, аккумуляторов (тогда только-только появились долговечные никель-водородные), полезной нагрузки и системы управления (ориентация батарей и преобразование энергии для нагрузки). Всё это прогонялось на заданном периоде времени под воздействием внешних метеоусловий в заданной местности. Для этого также была создана модель погоды (мною самостоятельно, через 7 лет после Брэдли Эфрона, переоткрытым) методом «статистический бутстрэп». При этом, в качестве исходного «кирпичика» для модели солнечной батареи (и батареи аккумуляторов) использовались модели реальных параметров кремниевых пластин (аккумуляторов), из которых собирались батареи с учётом их статистического разброса при производстве и схемы сборки. Модель автономной системы позволяла оценить размеры и конфигурацию солнечной и аккумуляторной батареи, достаточные для решения поставленных задач в заданных условиях функционирования системы (тут прямо физически узнал/вспомнил суконную речь полковника Первого отдела).

Измерения кремниевых пластин фотоэлементов на выходе техпроцесса и идентификация параметров модели единичного элемента методом оптимизации позволили создать массив параметров элементов, описывающий статистические параметры текущего техпроцесса производства солнечных элементов.

Математическая модель вольтамперных характеристик (ВАХ) солнечного элемента, хорошо известна, параметров там немного. Подобрать параметры модели ВАХ солнечного элемента с минимальным среднеквадратичным отклонением — это классическая задача поиска минимума целевой функции (суммарный квадрат отклонений на ВАХ).

Полученные методом Монте-Карло параметры готовой солнечной батареи отражали возможный стохастический разброс её параметров при заданной структуре соединения элементов. Построение модели батареи, собранной из моделей солнечных элементов, позволяло, в частности, решать и задачи оценки потерь мощности батареи при повреждениях (война в Афганистане была в разгаре, а в космосе метеориты летают), и потерь из-за частичного затенения (снег, листва), что приводило к возникновению опасных пробойных напряжений и необходимости грамотно размещать шунтирующие диоды для уменьшения потерь мощности в среднем. Всё это были уже стохастические задачи, т.е. требующие огромного объёма вычислений с разным разбросом исходных параметров «кирпичиков», схем соединения батареи и воздействующих факторов. «Плясать» от первичной идентифицированной модели солнечного элемента в таких расчётах было накладно, поэтому строилась цепочка моделей: первичной кремниевой пластины, блока из которых собиралась вся батарея (если требовался анализ структурной схемы), и самой батареи. Параметры этих моделей идентифицировались с помощью методов оптимизации, а массив элементов структуры батареи для её расчёта генерировался методом Монте-Карло с учётом стохастических вариаций (массив параметров + статистический бутстрэп).

Решаемые задачи всё усложнялись. В начале была идея самые «вычислительно-ёмкие» части методов оптимизации сделать на ассемблере, но по мере роста производительности сначала СМ-ЭВМ (задачи считались за ночь), а потом ПК (ныне самые сложные задачи требуют час-два), необходимость оптимизации программы оптимизации (шедевр тавтологии) отпала. К тому же, «вычислительно-ёмкими» оказываются в большинстве случаев сами целевые функции.

Здесь необходимо вернуться к частично уже затронутой универсальности методов оптимизации и соотнести их с другими методами численного анализа. Основные применения разработанного инструментария:

— идентификация параметров теоретической модели по исходным (экспериментальным или вычисленным) данным;
— аппроксимация данных, это та же идентификация только не модели, а параметров подходящей (в общем случае абстрактной) формулы, для целей сглаживания/аппроксимации, интерполяции и экстраполяции;
— численное решение систем произвольных (!) уравнений.

Вроде бы немного, но этот класс задач «накрывает» большой спектр реальных прикладных задач математики в промышленности, науке, пример с моделью автономной системы тому свидетельство.

В арсенале классических методов численного анализа есть эффективные прямые методы/подходы решения некоторых стандартных задач (например, систем уравнений с полиномами невысоких степеней), для них разработаны специальные библиотеки программ. Однако, когда число параметров/неизвестных превышает 4-5 (и вычислительные затраты катастрофически нарастают), и/или когда вид уравнений далёк от классических (не полиномы и т.п.), а в жизни, как правило, всё сложнее (исходные данные зашумлены погрешностями и ошибками измерений), готовые библиотеки программ оказываются малоэффективны.

Приведу поподробнее ещё один пример из относительно недавнего применения разработанного инструментария для решения задач оптимизации из жизни.
Для некоей диссертации по экспериментальным (полевым) данным требовалась идентификация теоретической модели, которая должна была эти данные описать и позволяла дать реальные рекомендации по повышению эффективности смежного технологического процесса. Каждый процент улучшения техпроцесса оправдывал неоднократное путешествие на полевые испытания (и близлежащие пляжи) первым классом через полмира и приобретение шикарного джипа Лексус только для проезда по полям (да ещё и с приятной длинноногой блондинкой, умеющей не только варить борщ :). Проблема была в том, что таких моделей было несколько, выбрать применимость одной из них могла идентификация и качество воспроизведения данных эксперимента, а параметров в этих моделях было от 6 до 9, и потенциально наиболее полезная модель по закону бутерброда была самой сложной.

Ниже приводятся исходные экспериментальные данные (X,Y,Z), 19 измерений:

И пример аппроксимации кривой (U3 — эксперимент, U3R — расчёт по модели) при идентификации самой сложной девяти-параметрической модели (a1. a9 — параметры модели):

Формула этой модели:

Если у вас возникает потребность в подобных работах — я мог бы делать расчёты по предоставленным данным и прислать результаты электронной почтой, чтобы оценить преимущества разработанного мат. аппарата.

Это востребованный спектр задач в науке, на производстве, при подготовке диссертаций, серьёзных дипломов, обработке данных, построении моделей. Причём какой-либо обман исключён, ибо по предоставленным результатам каждый может сам оценить достигнутую реально точность расчёта.

Опишите ваши проблемы в обработке данных — и я найду, как получить решение, программа должна работать!
Заинтересован получить взгляд со стороны на описанное, возможно, на новые сферы применения. Буду признателен за полезные замечания и кооперацию.

Источник

1. Введение в методы оптимизации

Оптимизация – это процесс выбора наилучшего варианта или процесс приведения системы в наилучшее (оптимальное) состояние, который состоит в нахождении всех максимизирующих или минимизирующих элементов или седловых точек. Оптимизация лежит в основе экономического анализа. В пассивных экономических моделях (таких, как изучающие общее равновесие) нас интересует оптимальное поведение лица, принимающего решение. В активных моделях (таких, как модели эффективного роста) мы сами заинтересованы в получении оптимума. В последние годы появилась тенденция к переходу от моделей типа «затраты – выпуск» к моделям анализа производственных процессов, от простейших моделей роста к моделям, изучающим траектории оптимального и эффективного роста.

Методы оптимизации – методы поиска экстремума функции (в практических задачах – критериев оптимальности) при наличии ограничений или без ограничений очень широко используются на практике. Это, прежде всего оптимальное проектирование (выбор наилучших номинальных технологических режимов, элементов конструкций, структуры технологических цепочек, условий экономической деятельности, повышение доходности и т. д.), оптимальное управление построением нематематических моделей объектов управления (минимизации невязок различной структуры модели и реального объекта) и многие другие аспекты решения экономических и социальных проблем (например, управление запасами, трудовыми ресурсами, транспортными потоками и т. д.).

Методы оптимизации являются разделом математического моделирования.

Эти темы охватывают широкий спектр различных задач математического моделирования, возникающих при исследовании реальных объектов промышленного производства, экономических, финансовых и других проблем.

Модель – это такой материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте–оригинале.

Для того чтобы использовать математические результаты и численные методы теории оптимизации для решения конкретных задач, необходимо:

 установить границы подлежащей оптимизации системы;

 определить количественный критерий, на основе которого можно произвести анализ вариантов с целью выявления «наилучшего»;

 осуществить выбор внутрисистемных переменных, которые используются для определения характеристик и идентификации вариантов;

 построить модель, отражающую взаимосвязи между переменными.

Эта последовательность действий составляет содержание Процесса постановки задачи оптимизации.

Рассмотрим некоторые встречающиеся в практической деятельности задачи математического моделирования в содержательной, а не в формальной математической трактовке.

Задачи оптимального распределения ресурсов. В общем ви­де эти задачи могут быть описаны следующим образом. Имеется некоторое количество ресурсов, под которыми можно понимать денежные средства, материальные ресурсы (например, сырье, по­луфабрикаты, трудовые ресурсы, различные виды оборудования и т. д.). Эти ресурсы необходимо распределить между различны­ми объектами их использования по отдельным промежуткам вре­мени или по различным объектам так, чтобы получить макси­мальную суммарную эффективность от выбранного способа распределения. Показателем эффективности может служить, на­пример, прибыль, товарная продукция, фондоотдача (задачи мак­симизации критерия оптимальности) или суммарные затраты, се­бестоимость, время выполнения данного объема работ и т. п. (задачи минимизации критерия оптимальности).

Имеется начальное количество средств Р0, которое необходи­мо распределить в течение П Лет между S предприятиями. Сред­ства ИKi (K = 1. N; I = 1. S), выделенные в K-м году I-му пред­приятию, приносят доход в размере Fki(Uki) и к концу года возвращаются в количестве Ki(Uki). В последующем распределе­нии доход может либо участвовать (частично или полностью), ли­бо не участвовать.

Требуется определить такой способ распределения ресурсов (количество средств, выделяемых каждому предприятию в каж­дом плановом году), чтобы суммарный доход от S предприятий за П Лет был максимальным. Следовательно, в качестве показателя эффективности процесса распределения ресурсов за П Лет прини­мается суммарный доход, полученный от S предприятий:

(1)

Количество ресурсов в начале K-го года будем характеризовать величиной Pn1 (параметр состояния). Управление на K-том Шаге состоит в выборе переменных Uk1, Uk2, …, Uks, обозначающих ресурсы, выделяемые в K-том Году I-му предприятию.

Если предположить, что доход в дальнейшем распределении не участвует, то уравнение состояния процесса имеет вид

(2)

Если же некоторая часть дохода участвует в дальнейшем рас­пределении в каком-нибудь году, то к правой части последнего равенства прибавляется соответствующая величина.

Требуется определить ПS Неотрицательных переменных ИKi, Удовлетворяющих условиям (2) и максимизирующих функ­цию (1).

Оптимальное управление запасами. Класс задач, в которых рассматривается оптимальное управление запасами, является од­ним из наиболее сложных. Это обусловлено тем, что в задачах управления запасами процесс, естественно, разворачивается во времени, причем управление заключается в том, что решение на данном промежутке времени принимается с учетом того состоя­ния, к которому пришла система за предшествующие периоды. Кроме того, эти задачи связаны, как правило, с дискретным харак­тером переменных и, следовательно, решаются довольно сложно.

Проблема управления запасами является одной из важнейших областей практического приложения экономико-математических методов, в том числе методов математического программирова­ния.

При формулировке задач управления запасами используют следующие понятия.

Запасы — Это любые денежные или материальные ценности, которые периодически пополняются (производятся, доставляют­ся и т. д.) и некоторое время сохраняются с целью расходования их в последующие промежутки времени. Уровень запасов в лю­бой момент времени определяется начальным уровнем запасов плюс пополнение и минус расход за промежуток времени от на­чального момента до текущего.

Управление запасами в общем случае состоит в воздействии на соотношение между двумя основными факторами — пополне­нием и расходом. Цель управления — оптимизация некоторого критерия, зависящего от расходов на хранение запасов, стоимо­сти поставок, затрат, связанных с пополнением, штрафов и т. д.

В такой общей постановке подобные задачи могут иметь са­мое разнообразное практическое применение. Например, под за­пасами можно понимать продукцию предприятия, которая произ­водится непрерывно (пополнение) и отгружается потребителям определенными дискретными партиями (расход). При этом спрос на продукцию предполагается наперед заданным (детерминиро­ванный спрос) или подверженным случайным колебаниям (сто­хастическая задача). Управление запасами состоит в определении размеров необходимого выпуска продукции для удовлетворения заданного спроса. Цель — минимизация суммарных затрат на хранение и пополнение запасов.

Под запасами можно понимать запасы сырья или других мате­риалов, поставляемых дискретными партиями (пополнение), ко­торые должны обеспечить непрерывное потребление в процессе производства (расход). Критерием оптимальности могут служить суммарные затраты на хранение запасов, замораживание оборот­ных средств и поставки запасов.

Запасами могут быть товары, поставляемые в магазин опреде­ленными партиями и предназначенные для удовлетворения непрерывного, но подверженного случайным колебаниям поку­пательского спроса. Критерий оптимальности — суммарные за­траты на поставки, хранение запасов и изменение производствен­ного ритма; связи с вариациями спроса.

Запасами могут быть и сезонные товары, сохраняющиеся на складе ограниченной емкости. Товары можно покупать и прода­вать в различных количествах по ценам, меняющимся во време­ни. Задача состоит в определении политики покупок и продаж, обеспечивающих максимум суммарной прибыли, и является при­мером задачи складирования.

Задачи о замене. Одной из важных экономических проблем, с которыми приходится встречаться на практике, является опреде­ление оптимальной стратегии в замене старых станков, произ­водственных зданий, агрегатов, машин и т. д., другими словами, старого оборудования на новое.

Старение оборудования включает его физический и мораль­ный износ, в результате чего растут производственные затраты по выпуску продукции на старом оборудовании, увеличиваются за­траты на его ремонт и обслуживание, а вместе с тем снижаются производительность и так называемая ликвидная стоимость.

Наступает момент, когда старое оборудование более выгодно продать, заменить новым, чем эксплуатировать ценой больших затрат. При этом оборудование можно заменить либо новым обо­рудованием того же вида, либо новым, более совершенным в тех­ническом отношении с учетом технического прогресса.

Оптимальная стратегия замены оборудования состоит в опре­делении оптимальных сроков замены. Критерием оптимальности при определении сроков замены может служить либо прибыль от эксплуатации оборудования, которую следует максимизировать, либо суммарные затраты на эксплуатацию в течение рассматри­ваемого промежутка времени, подлежащие минимизации.

Задачи оптимального управления. Обычно к этому типу задач относят задачи, связанные с нахождением распределен­ного во времени непрерывного управляющего воздействия. В экономике это прежде всего задачи прогнозирования тенденций развития, долгосрочных инвестиций и др. Например задача опти­мизации суммарного фонда потребления, где в качестве управ­ляющего воздействия рассматривается величина инвестиций как функция времени (задача может быть сформулирована с учетом и без учета инвестиционного лага), задача максимизации дисконти­рованного потребления и т. д.

Все упомянутые классы задач (при этом их состав далеко не полон) требуют для своего решения применения специальных ма­тематических методов линейного и нелинейного программирова­ния, динамического программирования, принципа максимума и некоторых других. Составной частью вычислительных работ при решении рассмотренных проблем могут являться задачи решения нелинейных уравнений и их систем, вычисления интегралов, ре­шение дифференциальных уравнений и т. д.

Существует достаточно большое количество численных методов оптимизации. Основные из них можно Классифицировать следующим образом:

 по размерности решаемой задачи: одномерные и многомерные;

 по способу формирования шага многомерные методы делятся на следующие виды:

O по способу вычислений градиента: с парной пробой и с центральной пробой;

O по алгоритму коррекции шага;

O по алгоритму вычисления новой точки: одношаговые и многошаговые;

 безградиентные: с поочередным изменением переменных и с одновременным изменением переменных;

 случайного поиска: с чисто случайной стратегией и со смешанной стратегией;

 по наличию активных ограничений;

 без ограничений (безусловные);

 с ограничениями (условные);

 с ограничениями типа равенств;

 с ограничениями типа неравенств;

Методы одномерной оптимизации являются базой для некоторых «многомерных» методов. В многомерной градиентной оптимизации строится улучшающая последовательность в зависимости от скорости изменения критерия по различным направлениям. При этом под улучшающей последовательностью понимается такая последовательность Х0, х1, …, хI, …, в каждой точке которой значение критерия оптимальности лучше, чем в предыдущей. В безградиентных методах величина и направление шага к оптимуму при построении улучшающей последовательности формируется однозначно по определенным детерминированным функциям в зависимости от свойств критерия оптимальности в окрестности текущей точки без использования производных (т. е. градиента). Случайные методы используются в задачах высокой размерности. Многомерная условная оптимизация учитывает активные ограничения, выраженные в виде равенств и неравенств. В каждом из рассмотренных направлений имеется большое число методов, обладающих своими достоинствами и недостатками, которые зависят, прежде всего, от свойств функций, экстремум которых ищется. Одним из сравнительных показателей качества метода является количество значений функции, которое нужно вычислить для решения задачи с заданной погрешностью. Чем это число меньше, тем при прочих равных условиях эффективнее метод.

В теоретических и математических задачах принято рассматривать задачи оптимизации как задачи поиска минимума функции. Даже методы имеют общее название – методы спуска. Однако при решении реальных практических задач очень часто встречаются задачи и на максимум (например, максимизация дохода, объема выпуска и т. д.). Конечно, легко перейти от одного вида экстремума к другому путем смены знака у критерия оптимальности, но это делают в прикладных нематематических задачах не всегда, чтобы не терять содержательную нить задачи.

1. Почему необходимо использование математики в экономике?

2. Что такое математическая модель?

3. Как строится математическая модель экономического явления и объекта? Приведите пример построения модели.

4. Что такое оптимизация?

5. Какие существуют методы оптимизации?

6. Какие экономические задачи решаются методами оптимизации?

Источник