W cu2 2 что это за формула
Энергия поля конденсатора
Вся энергия заряженного конденсатора сосредотачивается в электрическом поле между его пластинами. Энергию, накопленную в конденсаторе, можно определить следующим образом. Представим себе, что мы заряжаем конденсатор не сразу, а постепенно, перенося электрические заряды с одной его пластины на другую.
При перенесении первого заряда работа, произведенная нами, будет небольшой. На перенесение второго заряда мы затратим больше энергии, так как в результате перенесения первого заряда между пластинами конденсатора будет уже существовать разность потенциалов, которую нам придется преодолевать, третий, четвертый и вообще каждый последующий заряд будет переносить все труднее и труднее, т. е. на перенесение их придется затрачивать все больше и больше энергии. Пусть мы перенесем таким образом некоторое количество электричества, которое мы обозначим буквой Q.
Вся энергия, затраченная нами при заряде конденсатора, сосредоточится в электрическом поле между его пластинами. Напряжение между пластинами конденсатора в конце заряда мы обозначим буквой U.
Как мы уже заметили, разность потенциалов в процессе заряда не остается постоянной, а постепенно увеличивается от нуля — в начале заряда — до своего конечного значения U.
Для упрощения вычисления энергии допустим, что мы перенесли весь электрический заряд Q с одной пластины конденсатора на другую не маленькими порциями, а сразу. Но при этом мы должны считать, что напряжение между пластинами конденсатора было не ноль, как в начале заряда, и не U, как в конце заряда, а равнялось среднему значению между нулем и U, т. е. половине U. Таким образом, энергия, запасенная в электрическом поле конденсатора, будет равна половине напряжения U, умноженной на общее количество перенесенного электричества Q.
Полученный результат мы можем записать в виде следующей математической формулы:
W = UQ/2 (1)
Если напряжение в этой формуле будет выражено в вольтах, а количество электричества — в кулонах, то энергия W получится в джоулях. Если мы вспомним, что заряд, накопленный на конденсаторе, равен Q = CU, то формулу (1) можно будет записать окончательно в следующем виде:
W = CU 2 /2 (2)
Выражение (2) говорит нам о том, что энергия, сосредоточенная в поле конденсатора, равна половине произведения емкости конденсатора на квадрат напряжения между его пластинами.
Этот вывод имеет очень важное значение при изучении раздела радиотехники о колебательных контурах.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
W=CU²/2. Что это за формула и что за значок W?
формула закона сохранения энергии.
Эквивале́нтность ма́ссы и эне́ргии — физическая концепция, согласно которой масса тела является мерой энергии, заключённой в нём. Энергия тела равна массе тела, умноженной на размерный множитель квадрата скорости света в вакууме:
где E — энергия тела, m — его масса, c — скорость света в вакууме, равная 299 792 458 м/с.
Данная концепция может быть интерпретирована двояко:
* с одной стороны, концепция означает, что масса неподвижного тела (так называемая масса покоя) является мерой внутренней энергии этого тела [1];
* с другой стороны, можно утверждать, что любому виду энергии соответствует некая масса. Например, было введено понятие релятивистской массы как характеристики кинетической энергии движущегося тела [2].
В современной теоретической физике концепцию эквивалентности массы и энергии обычно используют в первом смысле [3]. Главной причиной, почему приписывание массы любому виду энергии считается неудачным, является следующая из этого полная синонимичность понятий массы и энергии. Кроме того, неаккуратное использование такого принципа может запутывать и в конечном итоге не является оправданным. Таким образом, в настоящее время термин «релятивистская масса» в профессиональной литературе практически не встречается, а когда говорят о массе, имеют в виду массу покоящегося тела. В то же время термин «релятивистская масса» используется для качественных рассуждений в прикладных вопросах, а также в образовательном процессе и в научно-популярной литературе. При этом под этим термином понимается увеличение инертных свойств движущегося тела.
В наиболее универсальной форме принцип был сформулирован впервые Альбертом Эйнштейном в 1905 году, однако представления о связи энергии и инертных свойств тела развивались и в более ранних работах других исследователей.
Электроемкость конденсатора
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Электроемкость проводников
Проводники умеют не только проводить через себя электрический ток, но и накапливать заряд. Эта способность характеризуется таким параметром, как электроемкость.
Электроемкость
C = q/φ
С — электроемкость [Ф]
q — электрический заряд [Кл]
φ — потенциал [В]
Особенность этой величины в том, что она зависит от формы проводника. Для каждого вида проводников есть своя формула расчета электроемкости. Самая популярная — формула электроемкости шара.
Электроемкость шара
C = 4πεε0r
С — электроемкость [Ф]
ε — относительная диэлектрическая проницаемость среды [-]
ε0 — электрическая постоянная
r — радиус шара [м]
Конденсаторы
Способность накапливать заряд — полезная штука, поэтому люди придумали конденсаторы. Это такие устройства, которые помогают применять электрическую емкость проводников в практических целях.
Конденсатор состоит из двух проводящих пластин (обкладок), разделенных диэлектриком. Между проводящими пластинами образуется электрическое поле, все силовые линии которого идут от одной обкладки к другой.
Когда заряд накапливается на обкладках, происходит процесс под названием зарядка конденсатора. Заряды на разных обкладках равны по величине и противоположны по знаку.
Электроемкость конденсатора измеряется отношением заряда на одной из обкладок к разности потенциалов между обкладками:
Электроемкость конденсатора
C = q/U
С — электроемкость [Ф]
q — электрический заряд [Кл]
U — напряжение (разность потенциалов) [В]
По закону сохранения заряда, если обкладки заряженного конденсатора соединить проводником, то заряды нейтрализуются, переходя с одной обкладки на другую. Так происходит разрядка конденсатора.
Любой конденсатор имеет предел напряжения. Если оно окажется слишком большим, то случится пробой диэлектрика, то есть разрядка произойдет прямо через диэлектрик. Такой конденсатор больше работать не будет.
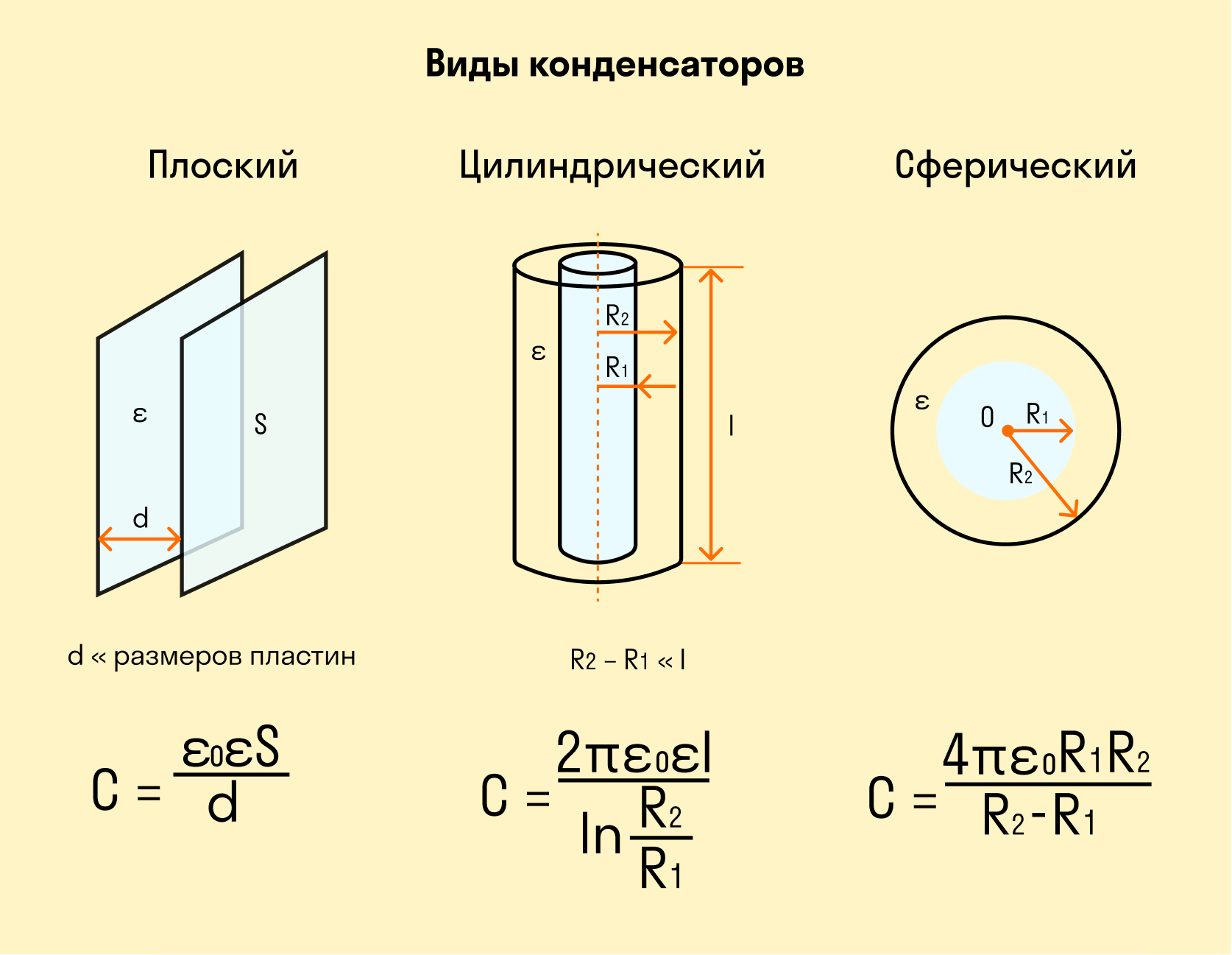
Виды конденсаторов
Энергия конденсатора
У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.
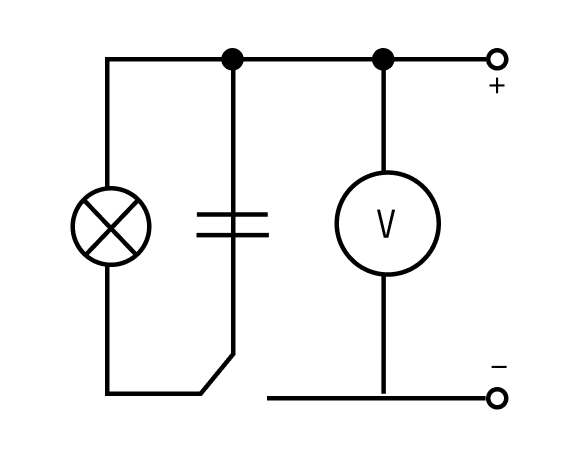
Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.
Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.
Энергия электростатического поля
Wp = qEd
Wp — энергия электростатического поля [Дж]
q — электрический заряд [Кл]
E — напряженность электрического поля [В/м]
d — расстояние от заряда [м]
В случае с конденсатором d будет представлять собой расстояние между пластинами.
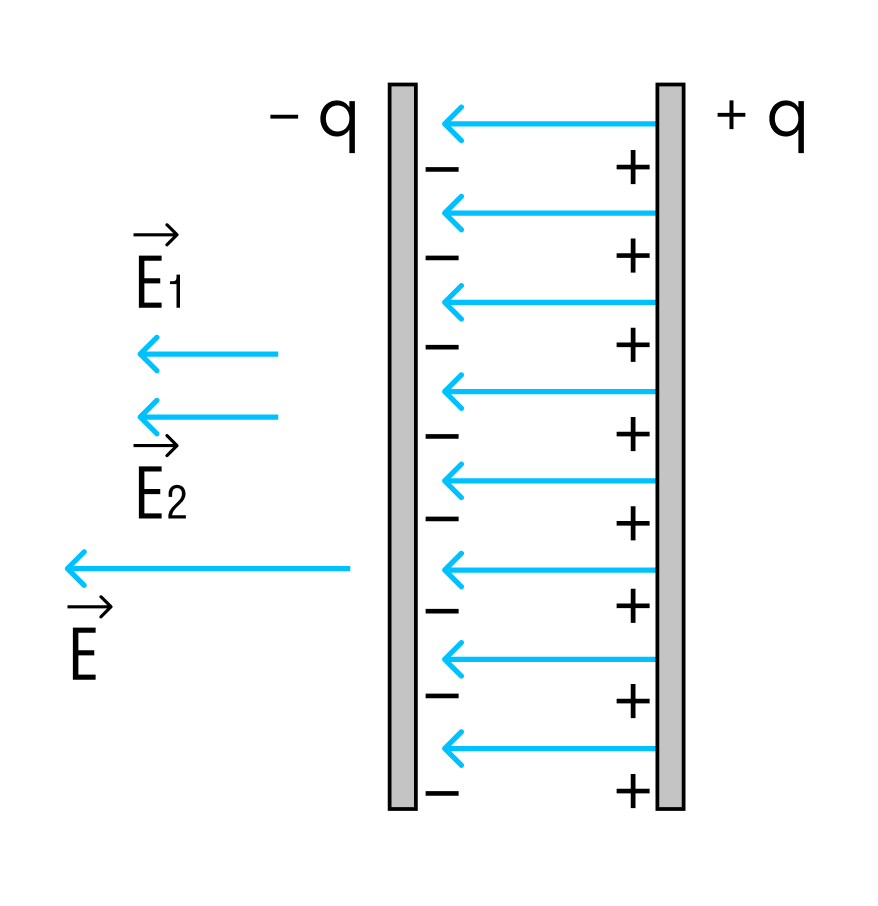
Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.
Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.
В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.
Тогда энергия конденсатора равна:
Wp = qEd/2
Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:
U = Ed
Wp = qU/2
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.
Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:
Энергия конденсатора
Wp = qU/2
Wp — энергия электростатического поля [Дж]
q — электрический заряд [Кл]
U — напряжение на конденсаторе [В]
Энергия конденсатора
Wp = q 2 /2C
Wp — энергия электростатического поля [Дж]
q — электрический заряд [Кл]
C — электроемкость конденсатора [Ф]
Энергия конденсатора
Wp = CU 2 /2
Wp — энергия электростатического поля [Дж]
C — электроемкость конденсатора [Ф]
U — напряжение на конденсаторе [В]
Эти формулы справедливы для любого конденсатора.
Применение конденсаторов
Конденсатор есть в каждом современном устройстве. Без него не будет работать ни один прибор. Разберем два самых наглядных примера.
Пример раз — вспышка
Без конденсатора вспышка в фотоаппарате работала бы не так, как мы привыкли, а с большими задержками, и к тому же быстро разряжала бы аккумулятор. Конденсатор в этом случае работает как батарейка. Он накапливает заряд от аккумулятора и хранит его до востребования. Когда нам нужна вспышка, конденсатор разряжается, чтобы она сработала и вылетела птичка.
Пример два — тачскрин
Тачскрин на телефоне работает по принципу, схожему с конденсатором. В самом смартфоне, конечно, тоже есть множество конденсаторов, но этот принцип куда интереснее.
Дело в том, что тело человека тоже умеет проводить электричество — у него даже есть сопротивление и электроемкость. Так что можно считать человеческий палец пластиной конденсатора — тело же проводник, почему бы и нет. Но если поднести палец к металлической пластине, получится плохой конденсатор.
В экран телефона встроена матрица из микроскопических пластинок. Когда мы подносим палец к одной из них, получается своего рода конденсатор. Когда перемещаем палец ближе к другой пластинке — еще один конденсатор. Телефон постоянно проверяет пластинки, и если обнаруживает, что у какой-то из них внезапно изменилась электроемкость, значит, рядом есть палец. Координаты пластинки с изменившейся электроемкостью передаются операционной системе телефона, а она уже решает, что с этими координатами делать.
Кстати, то же самое можно проделать, если взять обычную сосиску и поводить ей по экрану смартфона. Тачскрин будет реагировать на все контакты, как реагирует на человеческий палец.
Это не единственный вариант реализации тачскрина, но один из лучших на сегодняшний день. В айфоне используется именно он.
Изучать физику на примерах из реальной жизни может быть очень даже интересно. Попробуйте и убедитесь сами на классическом курсе по физике для 10 класса.
Закон Кулона, конденсатор, сила тока, закон Ома, закон Джоуля – Ленца
Теория к заданию 14 из ЕГЭ по физике
Закон Кулона
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.
В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.
Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
В аналитическом виде закон Кулона имеет вид:
Сила взаимодействия между зарядами зависит также от среды между заряженными телами.
В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.
Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.
Электрическая емкость конденсатора
Электроемкость
Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.
Электрический конденсатор
Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.
Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика. Проводники называются обкладками конденсатора. Как правило, расстояние между обкладками, равное толщине диэлектрика, намного меньше размеров самих обкладок, так что поле в конденсаторе практически все сосредоточено между его обкладками. Если обкладки являются плоскими пластинами, поле между ними однородно. Электроемкость плоского конденсатора определяется по формуле:
Под зарядом конденсатора понимают абсолютное значение заряда одной из пластин.
Энергия поля конденсатора
Энергия заряженного конденсатора выражается формулами
которые выводятся с учетом выражений для связи работы и напряжения и для емкости плоского конденсатора.
Сила тока
Электрическим током называется упорядоченное (направленное) движение заряженных частиц.
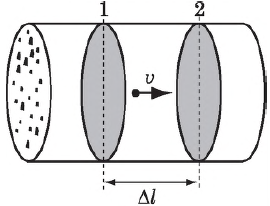
Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.
В СИ единица силы тока является основной и носит название ампер (А) в честь французского ученого А. М. Ампера (1755-1836).
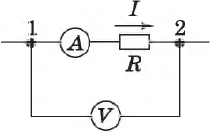
Силу тока измеряют амперметром. Принцип устройства амперметра основан на магнитном действии тока.
Закон Ома для участка цепи
Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.
Закон этот был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. В приведенной формулировке он называется также законом Ома для участка цепи. Математически закон Ома записывается в виде следующей формулы:
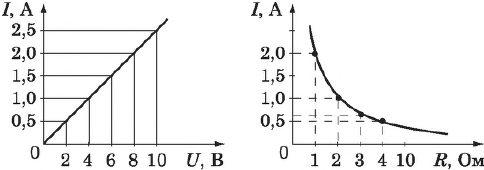
Зависимость силы тока от приложенной разности потенциалов на концах проводника называется вольт-амперной характеристикой (ВАХ) проводника.
Электрическое сопротивление
Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.
Удельное сопротивление
Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.
Зависимость сопротивления от температуры
С повышением температуры сопротивление металлов возрастает. Однако существуют сплавы, сопротивление которых почти не меняется при повышении температуры (например, константан, манганин и др.). Сопротивление же электролитов с повышением температуры уменьшается.
Зависимость удельного сопротивления проводников от температуры выражается формулой:
Таблица валентности химических элементов
Таблица валентности химических элементов.
Таблица валентности химических элементов:
Ниже приводится таблица валентности химических элементов с примерами соединений.
Валентность (от лат. valēns – «имеющий силу») – способность атомов химических элементов образовывать определённое число химических связей.
Валентность – это мера (численная характеристика) способности химических элементов образовывать определённое число химических связей.
Значения валентности записывают римскими цифрами I, II, III, IV, V, VI, VII, VIII.
Валентность определяют по числу химических связей, которые один атом образует с другими.
Таблица валентности химических элементов:
Первоначально за единицу валентности была принята валентность атома водорода. Валентность другого элемента можно при этом выразить числом атомов водорода, которое присоединяет к себе или замещает один атом этого другого элемента. Определенная таким образом валентность называется валентностью в водородных соединениях или валентностью по водороду: так, в соединениях HCl, H2O, NH3, CH4 валентность по водороду хлора равна единице, кислорода – двум, азота – трём, углерода – четырём.
Валентность кислорода, как правило, равна двум. Поэтому, зная состав или формулу кислородного соединения того или иного элемента, можно определить его валентность как удвоенное число атомов кислорода, которое может присоединять один атом данного элемента. Определенная таким образом валентность называется валентностью элемента в кислородных соединениях или валентностью по кислороду: так, в соединениях K2O, CO, N2O3, SiO2, SO3 валентность по кислороду калия равна единице, углерода – двум, азота – трём, кремния – четырём, серы – шести.
С точки зрения электронной теории валентность определяется числом неспаренных (валентных) электронов в основном или возбужденном состоянии.
Известны элементы, которые проявляют постоянную валентность. У большинства химических элементов валентность переменная.