Wgs 84 меркатор что это

СОДЕРЖАНИЕ

Характеристики

Формулы

Сферическая и эллипсоидальная смесь

Преимущества и недостатки

Однако, в отличие от эллипсоидального Меркатора, паутина Меркатора не совсем конформна. Это означает, что углы между линиями на поверхности не будут соответствовать одинаковым углам на карте, хотя они не будут отклоняться настолько, чтобы их можно было заметить невооруженным глазом. Линии отклоняются, потому что Web Mercator указывает, что координаты должны быть даны как измеренные на эллипсоидальной модели WGS 84. При проецировании координат, полученных при съемке, на эллипсоид, как если бы они были сняты на сфере, угловые соотношения немного меняются. Это стандартная практика для стандартной сферической проекции Меркатора, но, в отличие от Web Mercator, сферическая проекция Меркатора обычно не используется для карт локальных областей, таких как карты улиц, и поэтому точность положений, необходимых для построения, обычно меньше, чем угловое отклонение. вызвано использованием сферических формул. Преимущество Web Mercator заключается в том, что сферическую форму гораздо проще вычислить, чем эллипсоидальную форму, и поэтому требуется лишь небольшая часть вычислительных ресурсов.

Идентификаторы

Из-за медленного внедрения в реестр EPSG Web Mercator представлен несколькими разными именами и идентификаторами системы пространственной привязки (SRID), включая EPSG: 900913, EPSG: 3785 и EPSG: 3857.

EPSG: 900913

EPSG: 3785

В 2008 году EPSG предоставила официальный идентификатор EPSG: 3785 с официальным названием «Popular Visualization CRS / Mercator», но отметила: «Это не официальная геодезическая система». В этом определении использовалась сферическая (а не эллипсоидальная) модель Земли.

EPSG: 3857

Позже в том же году EPSG предоставила обновленный идентификатор EPSG: 3857 с официальным названием «WGS 84 / Pseudo-Mercator». В определении был использован эллипсоид WGS84 (EPSG: 4326), а не сфера.

Хотя прогноз тесно связан с Google, Microsoft указана как «источник информации» в стандартах EPSG.

Другие идентификаторы

Другие используемые идентификаторы включают ESRI: 102113, ESRI: 102100 и OSGEO: 41001.

ESRI: 102113 соответствует EPSG: 3785, а ESRI: 102100 соответствует EPSG: 3857.

WKT определение

Источник

Форумы GIS-Lab.info

Геоинформационные системы (ГИС) и Дистанционное зондирование Земли

Из Меркатора в WGS84 и обратно.

Из Меркатора в WGS84 и обратно.

Сообщение t[0]p » 12 сен 2017, 10:10

Re: Из Меркатора в WGS84 и обратно.

Сообщение freeExec » 12 сен 2017, 12:39

Re: Из Меркатора в WGS84 и обратно.

Сообщение ericsson » 12 сен 2017, 21:54

Re: Из Меркатора в WGS84 и обратно.

Сообщение t[0]p » 14 сен 2017, 14:18

Re: Из Меркатора в WGS84 и обратно.

Сообщение Andrey Zhukov » 14 сен 2017, 14:28

Re: Из Меркатора в WGS84 и обратно.

Сообщение konst555 » 14 сен 2017, 15:13

Re: Из Меркатора в WGS84 и обратно.

Сообщение Игорь Белов » 14 сен 2017, 21:03

Re: Из Меркатора в WGS84 и обратно.

Сообщение t[0]p » 15 сен 2017, 05:58

Re: Из Меркатора в WGS84 и обратно.

Сообщение Игорь Белов » 15 сен 2017, 09:39

Re: Из Меркатора в WGS84 и обратно.

Сообщение ericsson » 15 сен 2017, 11:31

Re: Из Меркатора в WGS84 и обратно.

Сообщение Ariki » 18 сен 2017, 12:08

Re: Из Меркатора в WGS84 и обратно.

Сообщение Ariki » 18 сен 2017, 13:54

Но ведь это неправда. Вы не сможете конформно изобразить чемодан на плоскости, пользуясь формулами проекции Меркатора или геометрическими построениями с использованием цилиндра.

Проекция EPSG:3857 основана на эллипсоиде WGS84, несмотря на то, что использует формулы для сферы. Если мы используем «честную» проекцию Меркатора на сфере, то порядок преобразований из WGS84 в координаты проекции такой:
1. Преобразуем геодезическую широту на эллипсоиде WGS84 в широту на сфере (для сферы геодезическая широта совпадает с геоцентрической).
2. Подставляем полученную широту и долготу в формулы проекции Меркатора для сферы. Эта проекция равноугольна по отношению к поверхности сферы.
Для EPSG:3857 первый шаг пропускается, то есть геодезическая широта на эллипсоиде WGS84 непосредственно подставляется в формулы сферической проекции Меркатора. Проекция не является равноугольной относительно поверхности эллипсоида, а поверхность сферы в этом случае вообще не имеет отношения к нашим координатам, заданным на эллипсоиде. В proj.4 пропуск первого шага реализуется через грязный хак с добавлением параметра

к определению проекции.

Я согласен с тем, что, поскольку Земля не является ни сферой, ни эллипсоидом, небольшие отклонения свойств проекции Pseudo Mercator от настоящей проекции Меркатора (на сфере или эллипсоиде) не являются практически значимыми в большинстве применений.

Источник

СОДЕРЖАНИЕ

Характеристики

Формулы

Сферическая и эллипсоидальная смесь

Преимущества и недостатки

Однако, в отличие от эллипсоидального Меркатора, паутина Меркатора не совсем конформна. Это означает, что углы между линиями на поверхности не будут соответствовать одинаковым углам на карте, хотя они не будут отклоняться настолько, чтобы их можно было заметить невооруженным глазом. Линии отклоняются, потому что Web Mercator указывает, что координаты должны быть даны как измеренные на эллипсоидальной модели WGS 84. При проецировании координат, полученных при съемке, на эллипсоид, как если бы они были сняты на сфере, угловые соотношения немного меняются. Это стандартная практика для стандартной сферической проекции Меркатора, но, в отличие от Web Mercator, сферическая проекция Меркатора обычно не используется для карт локальных областей, таких как карты улиц, и поэтому точность положений, необходимых для построения, обычно меньше, чем угловое отклонение. вызвано использованием сферических формул. Преимущество Web Mercator заключается в том, что сферическую форму гораздо проще вычислить, чем эллипсоидальную форму, и поэтому требуется лишь небольшая часть вычислительных ресурсов.

Идентификаторы

Из-за медленного внедрения в реестр EPSG Web Mercator представлен несколькими разными именами и идентификаторами системы пространственной привязки (SRID), включая EPSG: 900913, EPSG: 3785 и EPSG: 3857.

EPSG: 900913

EPSG: 3785

В 2008 году EPSG предоставила официальный идентификатор EPSG: 3785 с официальным названием «Popular Visualization CRS / Mercator», но отметила: «Это не официальная геодезическая система». В этом определении использовалась сферическая (а не эллипсоидальная) модель Земли.

EPSG: 3857

Позже в том же году EPSG предоставила обновленный идентификатор EPSG: 3857 с официальным названием «WGS 84 / Pseudo-Mercator». В определении был использован эллипсоид WGS84 (EPSG: 4326), а не сфера.

Хотя прогноз тесно связан с Google, Microsoft указана как «источник информации» в стандартах EPSG.

Другие идентификаторы

Другие используемые идентификаторы включают ESRI: 102113, ESRI: 102100 и OSGEO: 41001.

ESRI: 102113 соответствует EPSG: 3785, а ESRI: 102100 соответствует EPSG: 3857.

WKT определение

Источник

Google Web Mercator: неоднозначная система координат

Первого октября 2014 года американское Национальное Агентство Геопространственной Разведки (NGA) опубликовало отчет, в котором изложена критика системы координат Web Mercator, используемой во множестве картографических веб-сервисов. К документу прилагалось подробное разъяснение проблемы и рекомендации для партнеров NGA. Документ получил большой резонанс, но далеко не все статьи, основанные на этом отчете, отличались точностью и грамотностью изложения. Это касается, например, статьи на сайте ГИС Ассоциации, которую, по причине грубейших ошибок в терминологии, можно считать безграмотной. Поскольку именно с этой системой координат разработчики веб-сервисов сталкиваются чаще всего, я считаю, что есть смысл разобраться в проблеме.

Для начала — пара определений, без которых некоторые детали не могут быть ясны. Важно понимать, что Web Mercator — это система координат, а не только проекция, хотя ее название и напоминает известную многим проекцию Меркатора. Именно это терминологическое разночтение вводит в заблуждение читателей статьи на сайте ГИС Ассоциации. Разница между проекцией и системой координат состоит в том, что проекция — это только способ, которым сложная форма модели фигуры Земли разворачивается на плоскость, тогда как система координат включает в себя также математическое определение модели (эллипсоида или сфероида), аппроксимирующей сложную фигуру Земли.

На этой иллюстрации красным отмечено то, что относится только к механизму проекции (в данном случае — цилиндрической). К системе координат же относится вообще все, что здесь изображено.

В свою очередь, именно эта самая аппроксимирующая модель поверхности (пунктирная сфера на рисунке выше, на которой определены координаты λ,φ) и является источником проблемы, о которой дальше пойдет речь.

Я не могу сказать достоверно, кому первому и когда все это пришло в голову. Но, на сколько мне известно, первым крупным проектом, который стал использовать систему координат Web Mercator, был сервис Google Maps, и случилось это в 2005 году. Перед разработчиками стояла тогда задача упростить вычисления, необходимые для работы с картографическими данными, и самое очевидное, что можно было сделать — это использовать в системе координат сферу вместо эллипсоида. Занятно, что сам Герард Меркатор, скорее всего, исходил из таких же геометрических представлений, создавая свой способ проецирования карт на плоскость, потому что только Ньютон, живший несколько позже, предложил гипотезу о том, что Земля из-за центробежной силы имеет форму эллипсоида вращения, а не шара. Таким образом, разработчики Google, в каком-то смысле, вернулись в шестнадцатый век.

Критика в адрес этого подхода в профессиональных кругах звучит уже не в первый раз. Начиная с 2005 года, организация European Petroleum Survey Group (EPSG), занимающаяся стандартизацией в области систем координат и являющаяся держателем реестра их идентификаторов — кодов EPSG — отказывалась присвоить системе Web Mercator свой собственный официальный код, мотивируя это ее заведомым геометрическим несовершенством. Потому в сети можно встретить ссылки на эту систему через неофициальные коды: EPSG:900913, EPSG:102113 и другие. Однако, в 2008 году этой организации пришлось сдаться и присвоить код, так как популярность системы выросла, и ее нужно было как-то однозначно обозначать, чтобы не породить еще большую анархию. Первая попытка дать определение системе была не совсем удачной, но в конце концов ей был присвоен официальный SRID EPSG:3857.

Поскольку проекции — предмет изучения математики, я начну с формул, а потом дам им графическую иллюстрацию. Строго говоря, не обязательно даже хорошо владеть тригонометрией, чтобы понять разницу между реализацией систем координат на основе проекции Меркатора, сферы в одном случае и эллипсоида — в другом. Формулы заметно различаются внешне.
Проекция Меркатора эллипсоида на плоскость задается следующим образом:

где:
x и y — прямоугольные координаты,
λ — долгота на эллипсоиде в радианах,
φ — широта на эллипсоиде в радианах,
a — значение большой полуоси эллипсоида,
e — значение эксцентриситета эллипсоида (отношения большой и малой полуосей).

Если же вместо эллипсоида используется сфера, как это происходит в системе координат Web Mercator, все становится существенно проще, так как формула для ординат (оси Y) вырождается, давая следующее:

Согласитесь, выглядит куда проще и короче, чего и добивались разработчики Google. Это позволяет довольно заметно сократить количество математических операций при работе с картографическими материалами в клиентских и серверных приложениях.

Геометрия и картография

Даже если вообще не вдаваться в формулы, простые иллюстрации неплохо демонстрируют суть проблемы. Поясню сначала, что принцип построения проекции Меркатора состоит в том, что любая точка поверхности эллипсоида или сфероида проецируется на цилиндр, внутрь которого этот эллипсоид помещен так, чтобы их вертикальные оси совпадали, а поверхности либо касались по одной линии (наиболее частый случай), либо пересекались по двум. (Смотрите иллюстрацию выше). Далее, условные лучи проекции выходят из центра эллипсоида, пересекают его поверхность в точке P и попадают на поверхность цилиндра в точке P’, куда и переносится соответствующая точка поверхности Земли. Легко мысленно представить себе, что если реальная поверхность Земли при этом сначала спроецирована не на довольно близкий к ее форме эллипсоид, а на идеализированную сферу, то при проекции на цилиндр точек сферы, одни и те же исходные точки земной поверхности окажутся на ином расстоянии от линии экватора по вертикальной оси, чем в случае с эллипсоидом.

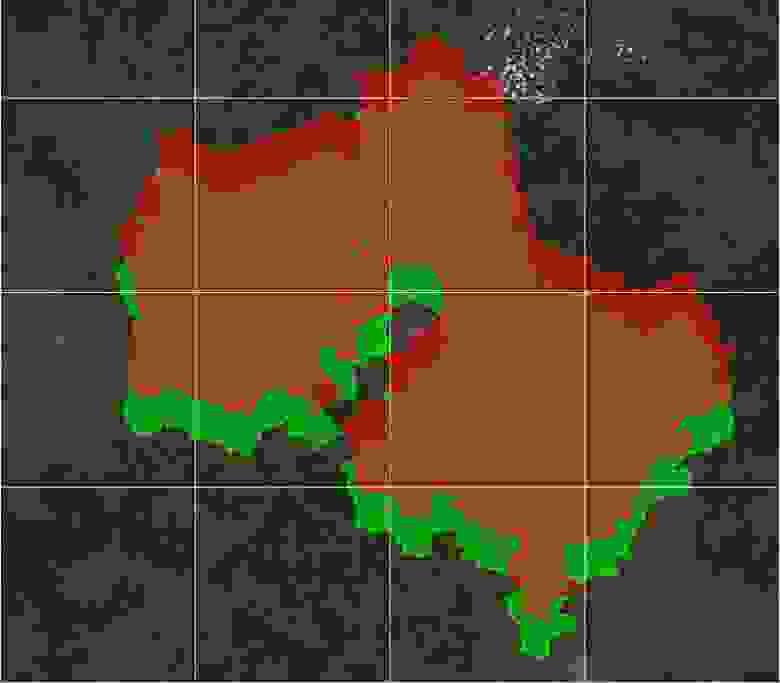
Попробую проиллюстрировать «масштабы бедствия». Возьмем в архиве NASA EOSDIS спутниковый снимок в естественных цветах Центрального Федерального округа России, сделанный аппаратом MODIS Aqua с разрешением 250 метров на пиксель 21 сентября 2014 года (именно этот день — потому что он был ясным, так будет красивее) — это будет наш фон.

Далее, запросом через Overpass Turbo выгрузим из базы OpenStreetMap административные границы Московской области в формате GeoJSON. Код запроса:

Теперь, используя Global Mapper, трансформируем данные границ Московской области из географической проекции в проекцию Меркатора эллипсоида WGS84. А далее, чтобы имитировать ситуацию, когда система координат будет опознана неправильно, скопируем получившиеся данные и вручную сменим определение системы координат на Web Mercator. В реальности, скорее, возможна обратная ситуация: данные в Web Mercator могут быть приняты за данные в WGS84/Mercator (это более чем возможно, потому что у Web Mercator есть еще куча названий, в некоторых из которых присутствует «WGS84»), однако от нашей имитации она будет отличаться только направлением сдвига. Получившиеся данные загрузим в Global Mapper, наложим поверх сетку с шагом 100 километров и посмотрим, что получилось.

Зеленый контур на карте находится там, где нужно, а красный — сдвинут. Величина этого сдвига — 19,6 километров. Это не значит, что такая ошибка существует во всех картографических сервисах, использующих эту систему координат, вовсе нет. Но она проявится в случае, если взять данные в этой системе и попытаться совместить с другими данными без ее верного учета. В этом случае, к ней будет применено неверное обратное преобразование в географические координаты, что и приведет к ошибке.

Некоторые картографические проекции обладают особыми свойствами, которые критичны для решения навигационных задач. Проекция Меркатора входит в их число, потому что ее широко используют для создания морских и аэронавигационных карт. Это возможно благодаря такому геометрическому свойству этой проекции, как конформность. В данном случае, оно означает, что форма объектов достаточно большого размера на этой карте сохраняется, так как сохраняются величины углов между линиями. Для навигации это означает, что глядя на карту, можно вычислить направление на искомую точку относительно меридиана (направления на географический север) и, двигаясь в этом направлении по магнитному компасу или под постоянным углом к линии на Полярную звезду, оказаться в нужном месте. Такой путь называется «локсодрома» и не является кратчайшим путем между двумя точками на поверхности Земли, а современные навигационные устройства позволяют вычислять путь по «ортодроме» — действительно кратчайшей линии, но от проекции Меркатора не отказываются, потому что карта, выполненная в ней, дает возможность в экстренной ситуации использовать для навигации подручные средства, не полагаясь на GPS-приемник и прочую электронику.

И вот здесь система координат Web Mercator оказывается обманчивой. Хотя она и основана на проекции Меркатора, но использование сферы с постоянным радиусом, как предельного упрощения модели поверхности Земли, лишает ее свойства конформности. Это значит, что двигаясь с постоянным курсовым углом, измеренным по такой карте, не удастся попасть в искомую точку из-за искажений углов в этой системе координат. Казалось бы, это не так важно для веб-сервисов, потому что по ним никто в своем уме не будет прокладывать путь в экстренной ситуации. Однако, разнообразие веб-сервисов велико, и гарантировать, что кто-то из разработчиков не вздумает считать какие-то направления в этой проекции — нельзя. При вычислениях в этой проекции ошибка может очень сильно накапливаться. Плюс, сейчас весьма популярны средства вроде САС.Планета, выкачивающие данные из веб-сервисов, и никто не может предугадать, что дальше с этими данным сделает пользователь.

Масштабы проблемы в данном случае тоже довольно легко измерить. Возьмем тот же снимок для фона, те же данные о положении административной границы Московской области. Теперь нам нужны три линии: ортодрома (кратчайшая с учетом кривизны Земли) и две локсодромы, построенные в системах Mercator/WGS84 и Web Mercator. Строить эти линии будем между самой южной точкой в Серебрянопрудском районе области, недалеко от населенного пункта с занятным названием «Мочилы» и самой северной — в Талдомском районе.

Построим ортодрому. Теперь измерим ее длину (получилось чуть меньше трехсот семи километров) и начальный угол относительно меридиана. Дальше — самое интересное. Перепроецируем рабочее пространство в проекцию Меркатора и построим из той же начальной исходной точки прямую в этой проекции линию, задав измеренный угол и длину 307 километров, не глядя, куда она попадет другим концом. Повторим то же самое, но в системе координат Web Mercator. Две локсодромы готовы. Для наглядности еще найдем на ортодроме центральную точку, поделив ее пополам и поставив в этом месте маркер. Перепроецируем рабочее пространство в UTM 37N WGS84, чтобы добиться минимального искажения углов, пропорций и прочих свойств карты.

В таком масштабе почти ничего нельзя разобрать — все линии практически сливаются. Но взглянем поближе на центр линий, включив предварительно сетку с шагом 100 метров.

Зеленая линия с черной точкой на карте — это ортодрома. Желтая — локсодрома, которая построена в Mercator/WGS84, красная — локсодрома в Web Mercator. Как и ожидалось, локсодромы ушли от ортодромы, потому что они не являются кратчайшими расстояниями и относительно прямой ортодромы являются дугами. Основательно ушли — более чем на 500 метров. Но куда же они нас привели?

Желтая локсодрома, построенная в проекции Меркатора эллипсоида WGS84, описав правильную дугу, «волшебным образом» вернулась к нужной точке. Это означает, что в данной проекции можно попасть в нужную точку, зная начальный курсовой угол и двигаясь все время под этим углом к направлению на географический север. А с красной так не вышло — она промахнулась более чем на полторы сотни метров. Полторы сотни на три сотни тысяч метров пути. Четыре сотых доли процента. Много это, или мало? Это достаточно, чтобы не считать ее конформной и не использовать для вычислений, где это важно.

Проблема с определением того, что используется система координат Web Mercator — не выдумана. Из-за ее, скажем так, «анархического» прошлого у нее столько имен, что все просто невозможно перечислить. Однако, я попробую продемонстрировать, на сколько все ужасно, перечислив только некоторые из известных имен и кодов этой системы координат:

Web Mercator, Google Web Mercator, Spherical Mercator, WGS 84 Web Mercator, WGS 84/Pseudo-Mercator (при том, что «псевдо» тут как раз не Меркатор, а WGS84), WGS84 Web Mercator (Auxiliary Sphere), Popular Visualisation CRS / Mercator, WGS84 / Simple Mercator.

EPSG:900913, EPSG:3785, EPSG:3857, EPSG:102113, ESPG:102100, EPSG:41001.

Вот так эта система выглядит в формате PROJ.4:
+proj=merc +lon_0=0 +k=1 +x_0=0 +y_0=0 +a=6378137 +b=6378137 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs
Здесь следует обратить внимание на равные значения параметров размеров полуосей эллипсоида a и b. Их равенство и означает использование сферы. В случае, если это «честная» проекция Меркатора эллипсоида WGS84, она же EPSG:3395, в формате PROJ.4 она определяется вот так:
+proj=merc +lon_0=0 +k=1 +x_0=0 +y_0=0 +ellps=WGS84 +datum=WGS84 +units=m +no_defs

Я не пытаюсь тут доказать, что система координат Web Mercator никуда не годится. Годится, конечно. И ровно тот же вывод (кроме вопросов, где важно соответствие военным стандартам США) можно обнаружить в отчете NGA. Просто важно понимать разницу между системами координат и их возможностями. Важно понимать, что Web Mercator используется почти везде: Google, OpenStreetMap, Bing, Yahoo и несчетное число других сервисов. Она также заложена в формат Slippy Map Tiles, в котором хранятся многие тайловые источники растровых данных. Она столь популярна, что далеко не все, кто ее используют, задумываются над тем, как же именно она устроена. А задуматься иногда стоит, особенно если планируемый сервис должен выполнять функции, более сложные чем простой показ картинки с картой.

Несколько занятных фактов вместо заключения

Агентство NGA, с отчета которого начался новый виток этой истории, до появления таких сервисов как NASA World Wind, Google Maps, Яндекс.Карты и других, было единственным доступным любому источником спутниковых снимков сравнительно высокого разрешения (10 метров на пиксель, черно-белое изображение) на территорию России, которые можно было бесплатно скачать через сервис NIMA Raster Roam (тогда NGA еще носило название NIMA — National Imagery and Mapping Agency). Эти снимки были частью разведывательной программы, выполнявшейся спутниками начиная с пятидесятых годов, и попавшие в программу рассекречивания в 1995 году.

Сервис Яндекс.Карты не использует систему координат Web Mercator, он использует честную проекцию Меркатора эллипсоида WGS84, код EPSG:3395. С чем это связано изначально, мне неизвестно, но было бы весьма интересно услышать комментарии сотрудников Яндекса, которые здесь, на Хабре, присутствуют в немалом количестве.

Местные картографические сервисы скандинавских стран часто не используют проекцию Меркатора вообще, предпочитая те системы координат, которые приняты в этих странах, например, норвежский государственный сервис Norge i Bilder использует три зоны проекции UTM и датум EUREF89. Это вызвано тем, что в северных широтах проекция Меркатора дает слишком сильные деформации масштаба.

Источник

Блог Алексея Воронина

История, краеведение, сельское хозяйство, лесоводство, биология, IT…

Практическая картография

В пеших путешествиях и велопоездках незаменимым спутником исследователя является топографическая карта. Одной из задач картографии (одной из дисциплин такой науки как геодезия) является изображение криволинейной поверхности Земли (фигуры Земли) на плоской карте. Для решения этой задачи необходимо выбрать эллипсоид — форму трехмерного тела, приближенно соответствующего земной поверхности, датум — начальную точку системы координат (центр эллипсоида) и начальный меридиан (англ. prime meridian) и проекцию — способ изображения поверхности этого тела на плоскости.

Эллипсоиды и датумы

В разное время для построения карт использовались различные варианты представления поверхности Земли в виде сферы или эллипсоида.

Одним из первых эллипсоидов был эллипсоид Бесселя (Bessel ellipsoid, Bessel 1841), определенный из измерений в 1841 году Фридрихом Бесселем (Friedrich Wilhelm Bessel), с длиной большой полуоси a = 6377397,155 м и сжатием f = 1:299,152815. В настоящее время он используется в Германии, Австрии, Чехии и некоторых азиатских и европейских странах.

Фридрих Бессель

датум Potsdam (PD)

Ранее для построения карт в проекции UTM использовался международный эллипсоид (International ellipsoid 1924, Hayford ellipsoid) с длиной большой (экваториальной) полуоси a = 6378388 м и сжатием f = 1:297,00, предложенный американским геодезистом Джоном Филлмором Хейфордом (John Fillmore Hayford) в 1910 году.

Джон Филлмор Хейфорд

датум ED 50 (European Datum 1950)

Для выполнения работ на всей территории СССР с 1946 года (постановление Совета Министров СССР от 7 апреля 1946 г. № 760) использовалась геодезическая система координат СК-42 (Пулково 1942), основанная на эллипсоиде Красовского с длиной большой (экваториальной) полуоси a = 6378245 м и сжатием f = 1:298,3. Этот референц-эллипсоид назван в честь советского астронома-геодезиста Феодосия Николаевича Красовского. Центр этого эллипсоида сдвинут по отношению у центру масс Земли примерно на 100 метров для максимального соответствия поверхности Земли на европейской территории СССР.

Феодосий Николаевич Красовский

датум Пулково-1942 (Pulkovo 1942)

В настоящее время (в том числе и в системе GPS) широко используется эллипсоид WGS84 (World Geodetic System 1984) с длиной большой полуоси a = 6378137 м, сжатием f = 1:298,257223563 и эксцентрисетом e = 0,081819191. Центр этого эллипсоида совпадает с центром масс Земли.

датум WGS84 (EPSG:4326)

Центр системы координат WGS84 совпадает с центром масс Земли, ось Z системы координат направлена на опорный полюс (англ. IERS Reference Pole (IRP)) и совпадает с осью вращения эллипсоида, ось X проходит по линии пересечения нулевого меридиана и плоскости, проходящей через точку начала координат и перпендикулярную к оси Z, ось Y перпедикулярна оси X.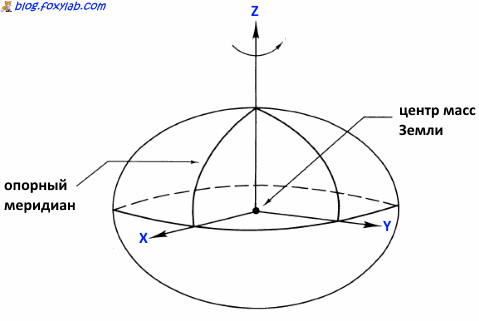

система координат WGS84

Альтернативой эллипсоиду WGS84 является эллипсоид ПЗ-90, используемый в системе ГЛОНАСС, с длиной большой полуоси a = 6378136 м и сжатием f = 1:298,25784.

Набор из указанных пяти параметров (dX, dY, dZ, da, df) может вводиться в навигатор или навигационную программу в качестве характеристики используемого пользователем датума.

Проекции

Способ изображения трехмерной земной поверхности на двумерной карте определяется выбранной картографической проекцией.
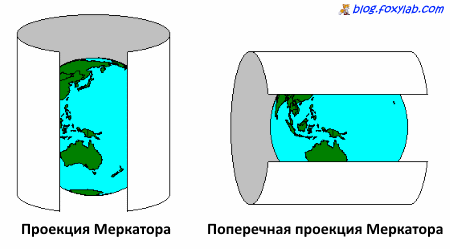
Наиболее популярны (нормальная) цилиндрическая проекция Меркатора и такая ее разновидность как поперечно-цилиндрическая проекция Меркатора (Transverse Mercator).

Герард Меркатор

В отличие от известной в течение веков нормальной проекции Меркатора, которая особенно хороша для изображения экваториальных областей, поперечная проекция отличается тем, что цилиндр, на который проецируется поверхность планеты, повернут на 90°:

Цилиндрическая проекция Меркатора

Сферическая проекция Меркатора

Вариант меркаторовской сферической проекции используется многими картографическими сервисами, например, OpenStreetMap, Google Maps, Bing Maps.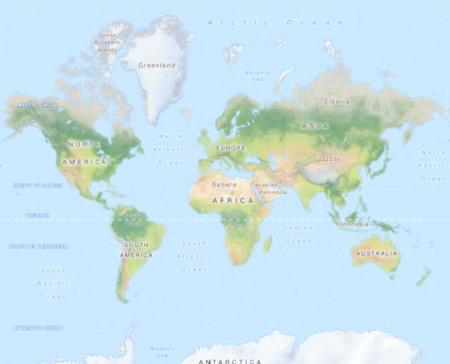

карта мира в OpenStreetMap

Эллиптическая проекция Меркатора

Поперечно-цилиндрическая проекция Меркатора

Чаще всего используются две разновидности поперечно-цилиндрической проекции Меркатора — проекция Гаусса-Крюгера (англ. Gauss — Krüger) (получила распространение на территории бывшего СССР) и универсальная поперечная проекция Меркатора (англ. Universal Transverse Mercator (UTM)).
Для обеих проекций цилиндр, на который происходит проекция, охватывает земной эллипсоид по меридиану, называемому центральным (осевым) меридианом (англ. central meridian, longitude origin) зоны. Зона (англ. zone) — это участок земной поверхности, ограниченный двумя меридианами с разностью долготы в 6°. Всего существует 60 зон. Зоны полностью покрывают поверхность Земли между широтами 80°S и 84°N.
Отличие двух проекций заключается в том, что проекция Гаусса-Крюгера — это проекция на касательный цилиндр, а универсальная поперечная проекция Меркатора — это проекция на секущий цилиндр (для избежания искажений на крайних меридианах):

Проекция Гаусса-Крюгера была разработана немецкими учёными Карлом Гауссом и Луи Крюгером.
В этой проекции зоны нумеруются с запада на восток, начиная с меридиана 0°. Например, зона 1 простирается с меридиана 0° до меридиана 6°, ее центральный меридиан 3°.
В советской системе разграфки и номенклатуры топографических карт зоны называются колоннами и нумеруются с запада на восток, начиная с меридиана 180°.
Например, Гомель и окрестности относятся к зоне 6 (колонне 36) с центральным меридианом 33°.
Зоны/колонны делятся параллелями на ряды (через 4°), которые обозначаются заглавными латинскими буквами от А до V, начиная от экватора к полюсам.
Например, Гомель и окрестности относятся к ряду N. Таким образом, полное название листа карты масштаба 1:1 000 000 (10 км в 1 см), изображающей Гомель, выглядит как N-36. Этот лист делится на листы карт более крупного масштаба: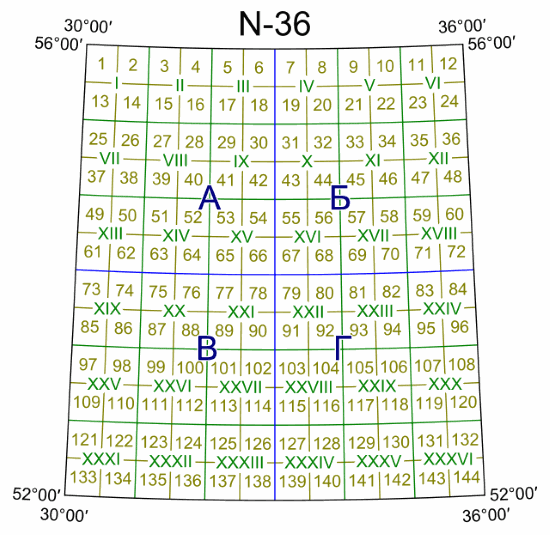

Для Беларуси и соседних стран разграфка такова: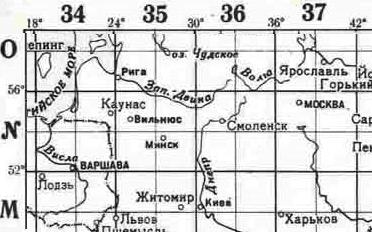

Для определения по топографической карте положения точки на карту наносят сетку прямоугольных координат X и Y, выраженных в километрах. Она образована системой линий, параллельных изображению осевого меридиана зоны (вертикальные линии сетки, оси X) и перпендикулярных к нему (горизонтальные линии сетки, оси Y).
На карте масштаба 1:200 000 расстояние между линиями сетки составляет 4 км; на карте масштаба 1:100 000 — 2 км.
Координата X подписывается на вертикальных краях листа карты и выражает расстояние до экватора, а координата Y подписывается на горизонтальных краях листа карты и состоит из номера зоны (первые одна или две цифры значения) и положения точки относительно центрального меридиана зоны (последние три цифры значения, причем центральному меридиану зоны присваивается значение 500 км).

фрагмент листа N36-123 советской топографической карты масштаба 1:100 000

Например, на вышеприведенном фрагменте карты надпись 6366 возле вертикальной линии сетки означает: 6 — 6-я зона, 366 — расстояние в километрах от осевого меридиана, условно перенесенного западнее на 500 км, а надпись 5804 возле горизонтальной линии сетки означает расстояние от экватора в километрах.

Универсальная поперечная проекция Меркатора

Универсальная поперечная проекция Меркатора (UTM) была разработана инженерными войсками США (United States Army Corps of Engineers) в 1940-х годах.

эмблема U.S. Army Corps of Engineers

Для построения карт в проекции UTM ранее использовался эллипсоид International 1924 — сетка UTM (International), а в настоящее время — эллипсоид WGS84 — сетка UTM (WGS84).
В этой проекции зоны нумеруются с запада на восток, начиная с меридиана 180°.
Эта система используется вооруженными силами США и НАТО (англ. United States and NATO armed forces):

Каждая зона разделена на горизонтальные полосы через каждые 8° широты. Эти полосы обозначены буквами, с юга на север, начиная от буквы C для широты 80° S и заканчивая буквой X для широты 84° N. Буквы I и O пропущены для избежания путаницы с цифрами 1 и 0. Полоса, помеченная буквой X, занимает 12° по широте.
Зона в этой проекции обозначается номером (англ. longitude zone) и буквой (каналом широты, англ. latitude zone):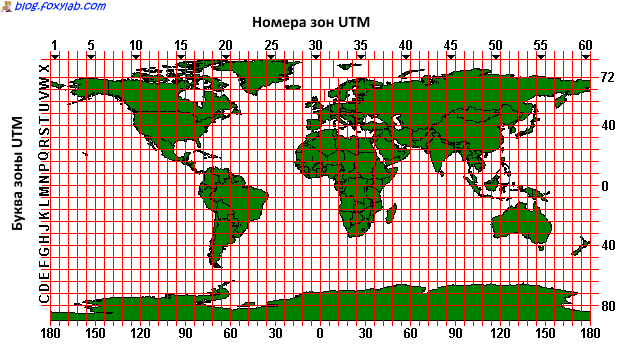

На этом рисунке видны две нестандартные зоны долготы — зона 32V расширена для покрытия всей южной Норвегии, а зона 31V сокращена для покрытия только водного пространства.
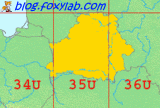
Для Гомеля и окрестностей зона обозначается как 36U с центральным меридианом 33°:

Зона покрывается прямоугольной (километровой) сеткой (сеткой по универсальной поперечной проекции Меркатора, СУППМ):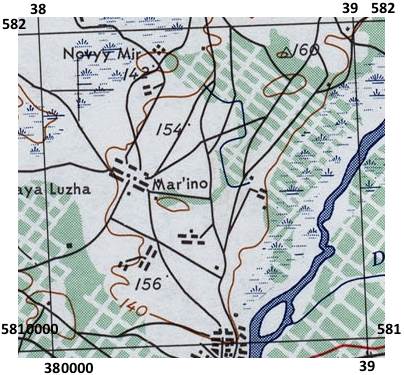

Длина стороны квадрата сетки в вышеприведенном фрагменте карты составляет 10 км.

Точка начала системы координат для каждой зоны определяется пересечением экватора и центрального меридиана зоны.
Координата E (Easting) на такой сетке представляет собой расстояние на карте от центрального меридиана в метрах (к востоку — положительное, к западу — отрицательное), к которому прибавлено + 500 000 метров (англ. False Easting) для избежания появления отрицательных значений.
Координата N (Northing) на такой сетке представляет собой расстояние на карте от экватора в метрах (к северу — положительное, к югу — отрицательное), причем в южном полушарии это расстояние вычитается из 10 000 000 метров (англ. False Northing) для избежания появления отрицательных значений.
Например, для левого нижнего угла квадрата сетки на вышеприведенной карте координаты записываются как
36U (либо 36+) 380000 5810000 ,
где 36 — longitude zone, U — latitude zone, 380000 — easting, 5810000 — northing.

Преобразование широты и долготы в координаты UTM поясняется рисунком:

Примечание. Погрешность считывания координат с карты (georeferencing accuracy) обычно принимается равной ±0,2 мм. Именно такую точность имеют устройства, применяемые при создании аналоговой карты.

Геоид

Продолжение следует.

Практическая картография : 4 комментария

Неправильное определения датума, надо смотреть буржуйское определение, так как слово буржуйское:
«A geodetic datum (plural datums, not data) is a reference from which measurements are made. In surveying and geodesy, a datum is a set of reference points on the Earth’s surface against which position measurements are made, and (often) an associated model of the shape of the earth (reference ellipsoid) to define a geographic coordinate system.»

То есть, в двух словах, датум — это математический эллипсоид, привязанный в пространстве относительно множества реально существующих точек (реперов), закрепленных на поверхности земли.
Начальный меридиан и проекция к датуму никакого отношения не имеют. Проекций на один и тот же эллипсоид может быть множество.

Спасибо за Ваш комментарий!
Моё мнение такое — датум = эллипсоид, у которого задан центр и начальный меридиан (пример датума — WGS84).
Про отношение проекции к датуму я и не писал (там просто перечисление — «эллипсоид», «датум», «проекция»).

Алексей очень подробная и полезная статья-спасибо! Помогите разобраться с задачей. У меня есть две точки с GPS координатами и из каждой точки направление на искомую точку. Известны углы и расстояние между точками, координаты, которых даны. Могу решить треугольник и определить все его стороны. Всё это на расстояниях не больше 2 км. Как мне получить GPS координаты искомой точки оптимальным способом, по каким формулам линейные значения в угловые переводить? В какой системе координат? Заранее спасибо!

Источник