Y sinx что за функция

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №4. Свойства и график функции .

Перечень вопросов, рассматриваемых в теме

Синусоидой называется множество точек плоскости, которое в некоторой системе координат является графиком функции , где a≠0.

Число │a│ называется амплитудой.

Колягин М.В. Ткачева Ю.М., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. М.: Просвещение, 2010.–336 с.

Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.

Открытые электронные ресурсы:

Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/

Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс]. – Режим доступа: https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

На прошлом уроке мы говорили о свойствах графика косинуса:

1) область определения функции – множество R всех действительных чисел;

2) Множество значений функции – отрезок [–1;1];

3) Функция косинуса периодическая, ;

5) Функция принимает:

;

6) Функция

Давайте сравним их со свойствами графика синуса, а для начала определим следующие моменты:

Свойства функции :

3) Период функции равен ;

4) Функция чётная/нечётная;

5) Функция принимает:

6) Функция

Изменяя амплитуду и значение аргумента функции синуса график ведет себя следующим образом (рис.1)

Рис. 1 – графики синуса

Сдвиг графика влево/вправо вдоль оси абсцисс

Если к аргументу функции добавляется постоянная, то происходит сдвиг (параллельный перенос) графика вдоль оси Ох.

Правило:
1) чтобы построить график функции , нужно сдвинуть график вдоль оси Ох на b единиц влево;

2) чтобы построить график функции , нужно график сдвинуть вдоль оси ОХ на b единиц вправо.

Теоретический материал для самостоятельного изучения

1. На следующие утверждения нужно ответить верно/неверно.

1) Тригонометрическая функция определена на всей числовой прямой.

2) График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.

3) График тригонометрической функции можно построить, используя одну главную полуволну.

Ответ: верно, неверно, верно.

2. Вспомним, что мы уже знаем о функции , ответив на вопросы:

1) Какие значения может принимать переменная х. Какова область определения этой функции?

2) В каком промежутке заключены значения выражения . Назови наибольшее и наименьшее значения функции .

3) Функция синуса чётная или нечётная?

Примеры и разборы решения заданий тренировочного модуля:

Пример 1. Найдем все корни уравнения , принадлежащие отрезку .

Построим графики функций и (рис. 6)

Рис. 7 – графики функций и .

Графики пересекаются в четырёх точках, абсциссы которых являются корнями уравнения . На выбранном отрезке от корни уравнения симметричны: и . Из рисунка видно, что симметричность корней объясняется периодичностью функции: аналогично для

Ответ: ; .

Пример 2.Найти все решения неравенства , принадлежащие отрезку .

Из рисунка 7 видно, что график функции лежит выше графика функции на промежутках и и

Ответ: , ,

Источник

14. Свойства функций синуса, косинуса, тангенса

и котангенса и их графики

14.1. СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК

График функции y = sin x (синусоида)

Свойства функции y = sin x

Объяснение и обоснование

Описывая свойства функций, мы будем чаще всего выделять такие их характеристики:

1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями

координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания * ;8) наибольшее и наименьшее

З а м е ч а н и е. Абсциссы точек пересечения графика функции с осью Ох

(то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.

Напомним, что значение синуса — это ордина-

та соответствующей точки единичной окружности

(рис. 79). Поскольку ординату можно найти для

любой точки единичной окружности (в силу того,

что через любую точку окружности всегда можно

провести единственную прямую, перпендикуляр-

ную оси ординат), то область определения функции

y = sin x — все действительные числа. Это можно за-

писать так: D (sin x) = R.

Для точек единичной окружности ординаты нахо-

дятся в промежутке [–1; 1] и принимают все значения

от –1 до 1, поскольку через любую точку отрезка [–1; 1]

оси ординат (который является диаметром единичной

окружности) всегда можно провести прямую, перпендикулярную оси орди-

нат, и получить точку окружности, которая имеет рассматриваемую орди-

нату. Таким образом, для функции y = sin x область значений: y ∈ [–1; 1].

Это можно записать так: E (sin x) = [–1; 1].

Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда

соответствующей точкой единичной окружности является точка A, то есть при

Наименьшее значение функции sin x равно минус единице. Это значение

достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть

при

поэтому ее график симметричен относительно начала координат.

В § 13 было обосновано также, что синус — периодическая функция с наименьшим положительным периодом

k — любое натуральное число.

Чтобы найти точки пересечения графика функции с осями координат,

напомним, что на оси Oy значение x = 0. Тогда соответствующее значение

y = sin 0 = 0, то есть график функции y = sin x проходит через начало координат.

На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при

которых sin x, то есть ордината соответствующей точки единичной окруж­

ности, равна нулю. Это будет тогда и только тогда, когда на единичной окруж-

ности будут выбраны точки C или D, то есть при x = πk, k ∈ Z (см. рис. 79).

функции синус положительны (то есть ордината соответствующей точки

единичной окружности положительна) в I и II четвертях (рис. 80). Таким

образом, sin x > 0 при всех x ∈ (0; π), а также, учитывая период, при всех

x ∈ (2πk; π + 2πk), k ∈ Z.

Значения функции синус отрицательны (то есть ордината соответствую-

щей точки единичной окружности отрицательна) в III и IV четвертях, поэто-

Промежутки возрастания и убывания

Учитывая периодичность функции sin x с периодом T = 2π, достаточно

исследовать ее на возрастание и убывание на любом промежутке длиной

2π, например на промежутке

то при увеличении аргумента x (x ₂ > x ₁ ) ордината соответствующей точки единичной окружности увеличивается (то есть

sin x ₂ > sin x ₁ ), следовательно, на этом промежутке функция sin x возрастает. Учитывая периодичность функции sin x,

делаем вывод, что она такж е возрастает на каждом из промежутков

Если x ∈ (рис. 81, б), то при увеличении аргумента x (x ₂ > x ₁ ) ордината соответствующей точки единичной

окружности уменьшается (то есть sin x _{2 1} ), таким образом, на этом промежутке функция sin x убывает. Учитывая

периодичность функции sin x, делаем вывод, что она также убывает на каждом из промежутков

Проведенное исследование позволяет обоснованно построить график функции y = sin x. Учитывая периодичность этой

функции (с периодом 2π), д о статочно сначала построить график на любом промежутке длиной 2π, на пример на

промежутке [–π; π]. Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината

соответствующей точки единичной окружности. На рисунке 82 показано построение графика функции y = sin x на

промежутке [0; π]. Учитывая нечетность функции sin x (ее график симметричен относительно начала координат), для

построения графика на промежутке [–π; 0] отображаем полученную кривую симметрич но относительно начала координат

Поскольку мы построили график на

промежутке длиной 2π, то, учитывая

периодичность синуса (с периодом 2π),

повторяем вид графика на каждом про-

межутке длиной 2π (то есть переносим па-

раллельно график вдоль оси Ох на 2πk,

где k — целое число).

Получаем график, который называется

З а м е ч а н и е. Тригонометрические функции широко применяются в ма тематике, физике и технике. Например,

множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п.,

описываются функцией, которая задается формулой y = A sin (ωх + φ). Та кие процессы называют гармоническими

колебаниями. График функции y = A sin (ωx + φ) можно получить из синусоиды y = sin х сжатием или растяжением ее вдоль

координатных осей и параллельным пере носом вдоль оси Ох. Чаще всего гармоническое колебание является функцией

времени t. Тогда оно задается формулой y = A sin (ωt + φ), где А — амплитуда колебания, ω — частота, φ — начальная

фаза,

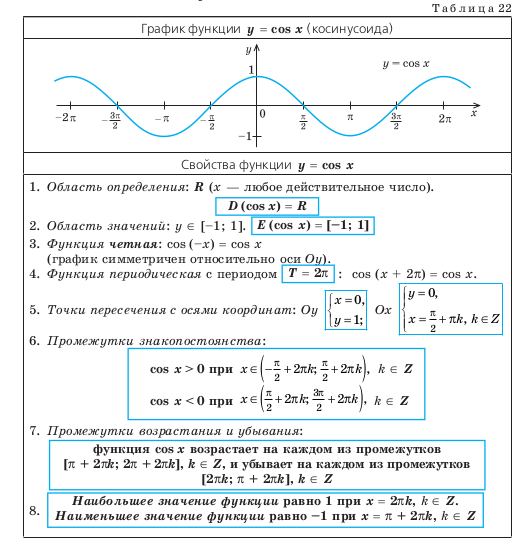
14.2. СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК

Объяснение и обоснование

Напомним, что значение косинуса — это абсцис-

са соответствующей точки единичной окружности

(рис. 85). Поскольку абсциссу можно найти для лю-

бой точки единичной окружности (в силу того, что

через любую точку окружности, всегда можно про-

вести единственную прямую, перпендикулярную оси

абсцисс), то область определения функции y = cos x —

все действительные числа. Это можно записать так:

D (cos x) = R.

Для точек единичной окружности абсциссы нахо-

дятся в промежутке [–1; 1] и принимают все значе-

ния от –1 до 1, поскольку через любую точку отрезка [–1; 1] оси абсцисс (который является диаметром единичной

всегда можно провести прямую, перпендикулярную оси абсцисс, и получить

точку окружности, которая имеет рассматриваемую абсциссу. Следователь но, область значений функции y = cos x:

y ∈ [–1; 1]. Это можно записать так: E (cos x) = [–1; 1]. Как видим, наибольшее значение функции cos x равно единице. Это

зна чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при

x = 2πk, k ∈ Z. Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда

соответствующей точкой единичной окруж ности является точка B, то есть при x = π + 2πk, k ∈ Z.

Как было показано в § 13, косинус — четная функция : cos (–x) = cos x, поэтому ее график симметричен относительно оси

Оу. В § 13 было обосновано также, что косинус — периодическая функция с наименьшим положительным периодом

T = 2π: cos (x + 2π) = cos x. Таким об разом, через промежутки длиной 2π вид графика функции cos x повторяется.

соответствующее значение y = cos 0 = 1. На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при

которых cos x, то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только

тогда, когда на единичной окружности будут выбраны точки C или D, то есть при

Промежутки знакопостоянства. Как было обосновано в § 13, значения

функции косинус положительны (то есть абсцисса соответствующей точки

единичной окружности положительна) в I и IV четвертях (рис. 86). Следова-

тельно, cos x > 0 при x ∈ (-П/2; П/2) а также, учитывая период, при всех

Значения функции косинус отрицательны (то есть абсцисса соответству-

ющей точки единичной окружности отрицательна) во ІІ и ІІІ четвертях,

поэтому cos x

Промежутки возрастания и убывания

Учитывая периодичность функции cos x (T = 2π), достаточно исследовать

ее на возрастание и убывание на любом промежутке длиной 2π, например

на промежутке [0; 2π].

Если x ∈ [0; π] (рис. 87, а), то при увеличении аргумента x (x ₂ > x ₁ ) абсцисса соответствующей точки единичной

окружности уменьшается (то есть cos x _{2 1} ), следовательно, на этом промежутке функция cos x убывает. Учитывая

периодичность функции cos x, делаем вывод, что она также убывает на каждом из промежутков [2πk; π + 2πk], k ∈ Z.

Если x ∈ [π; 2π] (рис. 87, б), то при увеличении аргумента x (x ₂ > x ₁ ) аб-

сцисса соответствующей точки единичной окружности увеличивается (то

есть cos x ₂ >cos x ₁ ), таким образом, на этом промежутке функция cos x

возрастает. Учитывая периодичность функции cos x, делаем вывод, что

она возрастает также на каждом из промежутков [π + 2πk; 2π + 2πk], k ∈ Z.

Проведенное исследование позволяет построить график функции y = cos x

аналогично тому, как был построен график функ-

ции y = sin x. Но график функции у = cos x можно

также получить с помощью геометрических преоб-

разований графика функции у = sin х, используя

Эту формулу можно обосновать, например, так.

Рассмотрим единичную окружность (рис. 88), отметим на ней точки

Источник

Функция y = sin x, её свойства и график

п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла

При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).

Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.

п.2. Свойства функции y=sinx⁡

2. Функция ограничена сверху и снизу

Область значений \(y\in[-1;1]\)

3. Функция нечётная

4. Функция периодическая с периодом 2π

5. Максимальные значения \(y_=1\) достигаются в точках

Минимальные значения \(y_=-1\) достигаются в точках

Нули функции \(y_<0>=sinx_0=0\) достигаются в точках \(x_0=\pi k\)

6. Функция возрастает на отрезках

Функция убывает на отрезках

7. Функция непрерывна.

п.3. Примеры

Пример 2. Решите уравнение графически:
a) \(sinx=3x\)

Один корень: x = 0

б) \(sinx=2x-2\pi\)

Один корень: x = π

в) \(sinx-\sqrt=0\)
\(sinx=\sqrt\)

Один корень: x = π

Источник