Адаптивная логика что это
Нечеткая логика на практике
Стандартная статья о нечеткой логике обычно грешит двумя вещами:
В нечеткой логике, в отличие от классической, вместо величин истина и ложь используется величина степень истинности, принимающая любые значения из бесконечного множества от 0 до 1 включительно. Следовательно логические операции уже нельзя представить таблично. В нечеткой логике они задаются фукнциями.
Есть два способа реализации дизъюнкции и конъюнкции:
Отрицание задается единственным способом (не трудно догадаться):
Легко проверить, что для крайних случаев — когда значения переменных исключительно 1 или 0 — приведенные выше функции дают таблицы истинности операций классической логики. Готово! Теперь у нас есть расширенная логика, обладающая невероятной мощью, простотой и при этом полностью совместимая с классической логикой в предельных случаях. Значит везде, где мы [программисты] используем логические выражения, мы можем использовать выражения нечеткой логики? Не совсем.
Дело в том, что все операторы языков программирования требуют четких условий, поэтому в какой-то момент всегда приходится из нечеткой степени истинности получать четкий критерий срабатывания. Это похоже на то, что происходит в квантовом мире: до тех пор, пока система эволюционирует в соответствии с уравнением Шредингера, ее квантовое состояние изменяется детерминированно и непрерывно, но как только мы прикасаемся к системе, происходит квантовый скачок, и система сваливается в одно из дискретных состояний. В нечеткой логике это называется дефаззификацией. Природа просто превращает квантовое состояние в вероятность и бросает кости, но вообще говоря методы дефаззификации бывают разные. Я не буду углубляться в эту тему, потому что объем ее тянет на отдельную статью. Упомяну лишь только, что метод дефаззификации следует выбирать, учитывая семантику задачи.
Для примера представим себе систему управления ракетой, использующую нечеткую логику для обхода препятствий. Представим себе, что ракета летит точно в гору, и система управления вычисляет решение: лететь вправо — 0.5, лететь влево — 0.5. Если использовать дефаззификацию методом центра масс, то система управления даст команду — лететь прямо. Бум! Очевидно, что в этом случае правильное решение — бросить кости и получить команду «влево» или «вправо» с вероятностью 50%.
В простейшем случае, когда нужно принять решение на основании степени истинности, можно разбить множество [0,1] на интервалы и использовать if-else-if.
Если нечеткая логика используется для поиска по нечеткому критерию, то дефаззификация вообще может быть не нужна. Производя сравнения, мы будем получать некоторое значение степени равенства для каждого элемента пространства поиска. Мы можем определить некоторую минимальную степень равенства, значения ниже которой нас не интересуют; для оставшихся элементов степень равенства будет релевантностью, по убыванию которой мы будем сортировать результаты, и пускай пользователь решит, какой результат правильный.
В качестве примера приведу использование нечеткой логики для решения задачи, которой я развлекался еще в институте — это задача поиска китайского иероглифа по изображению.
Я сразу отбросил идею распознавать любой каракуль, нарисованный пользователем на экране (тогда это был экран КПК). Вместо этого программа предлагала выбрать тип черты из порядка 23-х, определенных правилами японской каллиграфии. Выбрав тип черты, пользователь рисовал прямоугольник, в который вписывалась черта. Фактически, иероглиф — и введенный, и хранимый в словаре — представлялся в виде множества прямоугольников, для которых был определен тип.
Как определить равенство иероглифов в таком представлении? Для начала сформулируем критерий в четкой постановке:
Иероглифы A и B равны тогда и только тогда, когда для каждой черты в A существует равная ей черта в B и для каждой черты в B существует равная ей черта в A.
Неявно предполагается, что иероглифы не содержат черт-дубликатов, то есть, если некоторая черта совпала с чертой в другом иероглифе, то ни с одной другой чертой в том же иероглифе она совпасть не может.
Равенство черт можно определить следующим образом:
Черты равны тогда и только тогда, когда относятся к одному типу и их прямоугольники занимают одну и ту же площадь.
Эти два определения дают нам систему утверждений, которой достаточно для реализации алгоритма поиска.
Для начала построим матрицу E[n,n] следующим образом:
Затем сомкнем эту матрицу в вектор M[n]:
Я использую максиминный подход, потому что, на практике, колорометрический дает слишком маленькие значения для конъюнкций. Если вспомнить, что max — это дизъюнкция, то получается, что мы вычисляем утверждение, что i-я черта A равна первой черте B или второй или третьей и т.д. Таким образом M — это вектор совпадений черт A с чертами B.
Далее, нам нужно превратить вектор совпадений в одно единственное значение, и это можно сделать двумя способами:
Оба способа работают, но по-разному, причем второй способ работает даже если сравнивать черты четко. Какой из них правильней — вопрос философский.
Еще пару слов стоит сказать о сравнении черт. В соответствии с определением, равенство черт — это конъюнкция двух условий: равенства типов и равенства прямоугольников. Черты некоторых типов очень похожи. Вводя, пользователь легко может их перепутать, поэтому стоит иметь таблицу похожести, значения которой будут отражать насколько черта i похожа на черту j (на главной диагонали, естественно, будут единицы). Как степень равенства прямоугольников можно брать отношение площади их пересечения к площади большего из прямоугольников.
Вобщем, область применения нечеткой логики весьма обширна. В любом алгоритме, в любой системе правил попробуйте заменить истину и ложь на степень истинности и, возможно, эта система правил или алгоритм станут более точно отражать реальность. В конце концов, мы живем в мире, который фундаментально нечеток.
Поиск решений в логических играх на примере гомоку
Вступление
Вообще, речь пойдёт не о классической гомоку, а о русской вариации «пять в ряд». У вас есть листок бумаги в клеточку. Правила игры такие же, как в крестиках-ноликах. Отличие лишь в том, что необходимо выстроить линию из 5 элементов.
За такой нехитрой игрой мы прослушали не одну лекцию. Меня всегда раздражало, что моя блестящая стратегия разбивается о собственную невнимательность. Ну ничего, думал я, вот напишу программу, которая не будет делать ошибок, я тогда всем им покажу! Раз плюнуть! Пару циклов, правда, надо повозиться с пользовательским интерфейсом, но за пару вечеров управлюсь. С момента окончания института прошло 10 лет, а программу я всё ещё не написал.
Перебор в лоб
Идея состоит в том, что у нас нет никакой функции оценки, никакой эвристики. Мы просто расставляем элементы на поле, пока не достигнем пяти в линию. Сразу становится понятно, что такой метод не годится. Каждый ход в среднем генерирует 80 новых позиций. К 6 ходам количество вариантов возрастает до 80^6= 2^37 вариантов, что чересчур много.
Альфа-бета отсечение
Альфа-бета отсечение — это то, чем обычно ограничивается курс теории игр в институте. Применяется… честно говоря сложно придумать игру, в которой его можно применить. Возникает идея использовать функцию оценки в качестве критерия стоимости. Проблема в том, что нас по-настоящему интересует только победа или поражение. И нас вполне устроит победа за большее число шагов. Отсюда выплывает важное свойство: чтобы доказать победу с определённой позиции, достаточно найти один ход, а чтобы доказать поражение, необходимо перебрать все возможные ходы.
Решение с конца
Игра всегда заканчивается линией из 5 элементов. Если мы вернёмся на шаг назад, получим следующие комбинации:
Если вернуться на два шага назад, получим:
Линии можно комбинировать:
Весь набор комбинаций можно собрать в дерево поиска, которое разворачивается вокруг точки поиска.
Такое решение было реализовано, но работало медленно. Настолько медленно, что я так и не смог отладить код. Проблема в большом количестве комбинаций. Два шага назад — это всё, что ещё можно хранить в памяти.
Вычисление vs. хранение
После такого фейла я решил не хранить готовые шаблоны, а находить линии за один-два хода до победы «на лету». На удивление, это работало довольно неплохо. Вывод: иногда лучше решать, чем хранить.
В целях оптимизации я ограничил число возможных ходов двумя соседними клетками вокруг существующих. В общем-то, далеко не факт, что эффективные ходы ограничиваются этими клетками, но пока моё предположение неплохо согласуется с практикой.
В глубину или в ширину
Поиск в глубину предпочтительнее c точки зрения памяти, но часто уходит слишком глубоко, хотя победа находится рядом в соседней ветке. Поиск в ширину лишён этого недостатка, но требует много памяти для хранения уже решённых позиций. Обычно применяют форсированный поиск в глубину: поиск спускается на фиксированную глубину, но для перспективных позиций глубина увеличивается.
Оценочная функция
Существуют линии, на которые противнику необходимо реагировать.
Открытая четвёрка. Гарантированная победа, если противник не выигрывает на следующем ходу.
Закрытая четвёрка. Один ход до победы.
Открытая тройка. Два хода до победы.
Приоритет линий в таком порядке. Оценка хода увеличивается, если в одной точке сходятся несколько линий разных направлений. Также учитываются линии противника и защитные ходы на них.
Работает довольно хорошо. Программа играет на уровне новичка. Это 2 уровня поиска в ширину и 3 уровня форсированного поиска в глубину. К сожалению, этого совершенно недостаточно, чтобы выигрывать всегда. На этом идеи у меня закончились, и я уже было думал, что ничего существенно улучшить не получится. Если бы я не наткнулся на работу некоего Louis Victor Allis.
Mr. Allis и Treat-Space search
В 1992г. мистер Алис (Allis), используя 10 рабочих станций SUN SPARC, доказал для классического гомоку с полем 15X15, что крестики всегда побеждают. Станции имели 64 и 128MB RAM, 200MB свопа. Т.к. они использовали станции Vrije Universiteit в Амстердаме, их процессы запускались только ночью. Процессы, которые не завершились за ночь, на утро убивались. На всё ушло 1000 CPU/часов и неделя времени.

Начало цепочки угроз и её развитие

Анализ цепочки угроз. На первую угрозу, отвечаем сразу тремя защитными ходами. Несмотря на ответные ходы, возможно построение открытой четвёрки.
Такая эвристика позволяет нам эффективно искать цепочки угроз, на которые противник уже не в состоянии повлиять. Ответ одновременно всеми защитными ходами позволяет сделать сложность поиска практически линейной, а не комбинаторной. Конечно, каждую цепочку необходимо проверять на возможность контратак.
К сожалению, как проверять цепочки на возможность контратаки, я нифига не понял автор не уточнил. Поэтому пришлось лепить своё решение на коленке. На данный момент это самое медленное и стрёмное место в расчёте.
Эвристика нулевого хода
Лучше всего описана здесь.
Идея сводится к тому, что вы пропускаете свой ход, позволяя противнику сделать ход. Если ваша позиция всё ещё остаётся сильной, то, вероятно, данное состояние — не то, в которое противник позволит вам попасть. Это позволяет сэкономить один ход в глубину при анализе.
К сожалению, я не придумал как это безопасно и эффективно применить, поэтому пока не применяю.
Крестики выигрывают и дерево решений
С Treat-Space search эвристикой программа играет довольно сильно, но всё равно проигрывает сильному игроку. Это происходит потому, что программа способна «видеть» на 4 — 16 ходов вперёд. Иногда, особенно вначале партии, выгоднее ставить ходы на перспективу, а не пытаться развить локальное преимущество. Человек использует свой опыт, чтобы видеть направления, которые дадут преимущество в далёкой перспективе.
Так мы подходим к ещё одной проблеме компьютерных программ — недостаток опыта (lack of experience). Чтобы компенсировать это, в шахматных программах используется база дебютов. Можно подобное сделать игры «Пять в ряд». Проблема в том, что теорию гомоку я не осилил что теория для этой игры не так хорошо проработана, как для шахмат.
Поэтому возникает естественное желание перебрать дерево решений целиком, чтобы найти лучшие ходы. Как бонус можно получить доказательство, что крестики выигрывают, и оптимальную последовательность как бонус. Собственно это и сделал профессор Алис в своём исследовании.

Наиболее длинная цепочка при совершенной игре для гомоку без ограничений

Наиболее длинная цепочка при совершенной игре для гомоку с ограничениями
Согласно теории, поле 19X19 даёт крестикам большее преимущество, чем 15X15, поэтому для неограниченного поля всё должно быть ещё легче.
Распределённые вычисления на коленке
Расчёт продлился около месяца. К сожалению, чуда не произошло. К-во вариантов стабильно росло. Расчёт пришлось остановить. Даже на состояниях с 17-35 ходами дерево решений также стабильно расширяется.
Причина этого кроется в поиске в ширину. Мы затевали поиск в ширину, чтобы найти неочевидные решения.
Для этого приходится обходить все варианты, даже самые идиотские.
Алгоритм муравьиной колонии
Идеи у меня закончились, и я забросил проект почти на год, пока мой коллега не предложил мне использовать алгоритм муравьиной колонии.
Идея состоит в том, что мы случайным образом выбираем путь, который мы будет исследовать с определённого состояния. Вероятность хода зависит от соотношения числа побед/поражений всех потомков данной ветки.
Работает довольно неплохо. Проблема только в том, что нас не интересует, насколько вероятен проигрыш противника, если есть хотя бы одна позиция, в которой он может выиграть.
Спроси соседа про победу
Честно говоря, я не знаю, как называется эта эвристика. Она базируется на том факте, что для многих случаев ответные ходы противника не могут существенно повлиять на выигрыш.

Мы делаем «перспективный» ход ноликом. Вскоре обнаруживаем, что он ведёт к поражению за 17 ходов

Делаем очередной «перспективный» ход ноликом из этого же состояния. Обнаруживаем, что крестики снова выигрывают, причём тем же ходом
Для разных ходов ноликом, у нас один и тот же ответный ход крестиком. Можно просто увеличить вес уже известным победным ходам, чтобы сократить число перебираемых ходов.
Эта эвристика, в совокупности с алгоритмом муравьиной колонии, даёт огромной прирост производительности. Она настолько эффективна, что за день работы находит решённые позиции, начиная с четвёртого хода.
База дебютов и человек
Если мы хотим доказать, что крестики начинают и выигрывают, нам достаточно сделать один идеальный ход крестиком, на каждый возможный ход ноликом. Это эквивалентно уменьшению общей глубины поиска в два раза. В некоторых случаях, как на картинке выше, идеальные ходы очевидны для человека.
Я планирую добавить возможность избирательно форсировать вычисление определённых веток в надежде на то, что это даст мне существенный прирост в производительности.
А давайте перепишем на ассемблер
Ни в одном проекте я не пытался сделать столько оптимизаций и не испытывал столько разочарования.
Факты неумолимы: константа не имеет никакого значения по сравнению с общей сложностью алгоритма. Напомню, каждая позиция в среднем даёт 80 новых позиций. Чтобы продвинуться на один шаг вглубь, мы должны увеличить скорость работы программы в 80 раз.
Хотя алгоритмическая оптимизация себя ещё не исчерпала. И вполне возможно, что для задачи такой сложности достаточно одного современного смартфона.
Так что алгоритмы рулят!
Благодарности
Я благодарен д-ру Louis Victor Allis за его умение решать нерешаемые задачи.
Я безмерно благодарен всем тем людям из сообщества RSDN, которые помогали и продолжают помогать мне обсчитывать эту задачу, используя свои ресурсы.
Я благодарен Рустаму за идею с алгоритмом муравьиной колонии.
Я благодарен Ване за стилистическую и орфографическую корректировку статьи. Надеюсь, я ничего не пропустил из твоих правок.
8 задач на логику, которые предлагают на собеседованиях в ведущих IT-компаниях
1. Загадка о двух дверях
Эту задачку можно услышать в стенах цифрового гиганта Apple. Условие звучит так:
«Шелдон Купер (персонаж популярного сериала) прошел игровой квест до последнего рубежа. Теперь перед ним — две двери, одна из которых приведет к сокровищу, а вторая — в смертельно опасный лабиринт. У каждой двери стоит стражник, оба они знают, какая из них ведет к сокровищу. Вот только лишь один из них скажет правду. Шелдон не знает, кто из них врун, а кто нет. Прежде чем сделать выбор, можно поставить всего один вопрос и только одному стражнику.
Вопрос: Что нужно спросить Шелдону у стражника, чтобы найти путь к сокровищу?»
Ответ: Можно спросить любого, сформулировав вопрос так: «Какая дверь, по мнению другого стражника, правильная?». Если он спросит у «правдоруба», то узнает, какая дверь ведет к лабиринту, ведь врущий стражник всегда врет. Если же он спросит у лжеца, то снова узнает, какая дверь ведет к лабиринту, ведь тот соврет о двери, на которую укажет правдивый стражник.
2. Инопланетяне и шапки

Еще одна загадка для соискателей вакансий в Apple. Звучит она так:
«Землю захватили инопланетяне. Они хотят уничтожить всю планету, но решили дать человечеству один шанс. Они выбрали десять самых умных людей и поместили их в абсолютно темную комнату, выстроив в ряд. На каждого надели по шляпе, шляпы всего двух цветов — белые и черные. После того, как все шляпы оказываются на головах, свет включается.
Инопланетянин спрашивает последнего человека в ряду о цвете его шляпы. Ни о чем, кроме цвета шляпы, спрашивать нельзя, как и промолчать. Если он отвечает верно, остается в живых, ошибается — погибает. Цвет шляпа посмотреть нельзя, но можно договориться об определенном принципе, по которому могут ответить все. Расположение шляп — случайное, но вам видны все шляпы впереди.
Вопрос: Что нужно отвечать, чтобы выжило как можно больше людей?»
Ответ: Первый отвечающий считает количество черных шляп перед собой, если их нечетное число, он называет «черный», если четное — «белый». Следующий, видя шляпы перед собой, может таким образом вычислить, какого цвета головной убор у него на голове (к примеру, если черных все еще нечетное количество, то очевидно, что на нем — белая), и так далее. Таким методом сохраняется 9 из 10 человек.
3. Задание с мотоциклами

Эта задачка является частым гостем собеседований в компании Adobe:
«У вас есть пятьдесят мотоциклов полным баком, бензина в котором хватает на 100 км езды.
Вопрос: Как далеко вы сможете уехать с помощью этих пятидесяти мотоциклов (учитывая, что изначально они находятся в условно одной точке)?
Ответ: Сначала необходимо перевезти все мотоциклы на пятьдесят километров. Затем, топливо из половины мотоциклов перевивается во вторую половину. В результате мы имеем 25 мотоциклов с полным баком. Повторяйте процедуру каждый пятьдесят километров. Таким образом, можно проехать 350 км.
4. Задача о двух ведрах
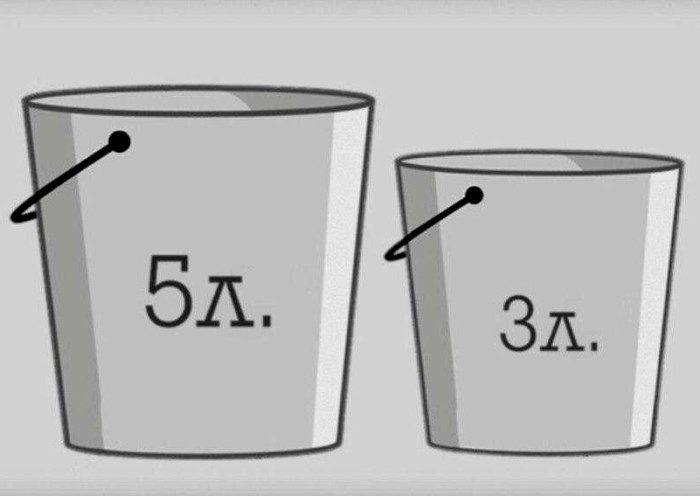
При отборе будущих сотрудников в корпорацию Microsoft используют следующую задачу:
«У вас есть бесконечный запас воды и два ведра объемом 5 литров и 3 литра соответственно.
Вопрос: Как с их помощью отмерить четыре литра?»
Ответ: Вначале наполните пятилитровое ведро и вылейте часть воды в трехлитровое. Теперь в большом ведре осталось два литра. Опустошите маленькое ведро и перелейте туда воду из большого. Снова заполните большое ведро и перелейте из него воду в меньшее. Так как в нем уже есть 2 литра, то после переливания в большом останется 4 литра.
5. Загадка о двух горящих веревках

Необычная задачка из стен офисов Microsoft:
«У вас есть два отрезка веревки. Длина каждого из них такова, что при поджигании любого из них с одного конца он будет гореть ровно шестьдесят минут.
Вопрос: Имея только коробок спичек, как отмерить с помощью двух отрезков такой веревки 45 минут при условии, что рвать веревки нельзя?»
Ответ: Одна из веревок поджигается с двух концов, одновременно с ней поджигается вторая, но уже с одного конца. Когда первый отрезок догорит, пройдет 30 минут, от первого также останется 30-минутный отрезок. Затем поджигаем оставшуюся веревку с двух концов, и она горит еще 15 минут.
6. Задача о восьми шариках

Неудивительно, что в таком информационном гиганте как Google, который способен генерировать любую информацию, есть загадки для собеседований. Условие звучит так:
«У вас имеется 8 шариков одинакового вида и размера.
Вопрос: Как найти более тяжелый шарик при условии, что использовать весы можно всего дважды?»
Ответ: Отберите шесть шариков, разделите их на группы по три шарика и поместите на весы. Те, что с более тяжелым шариком, перетянут чашу. Выберите из этой группы два любых шарика и снова взвесьте. Если тяжелый шарик среди них, вы это увидите, если они весят одинаково — тяжелым является третий шар группы. Если же более тяжелого шарика в группах по 3 шарика не оказалось, он — среди 2 оставшихся.
7. Лайфхак для собеседования от Илона Маска

Оказывается, у Илона Маска есть собственная любимая загадка на случай собеседования. Условия ее таковы:
«Представьте, что вы стоите на поверхности Земли. Вы проходите одну милю на юг, одну на запад и одну на север и оказываетесь в той же точке, откуда начали движение.
Вопрос: Где вы находитесь?»
Ответ: Их два. Первый способны дать большинство инженеров — это Северный полюс. Если с Северного полюса пройти одну милю на юг, потом повернуть на запад и пройти еще одну милю, а затем сменить направление на северное, то через одну милю вы снова окажетесь на Северном полюсе, замкнув своим движением треугольник.
Второй верный ответ на загадку — вблизи Южного полюса, на одну милю севернее параллели, длина которой равна одной миле.
8. Задача-бонус

А эту задачу мы предлагаем вас решить самостоятельно. Она интересна одной своей историей: ее предполагаемыми авторами называют не то Альберта Эйнштейна, не то Льюиса Кэрролла.
«На улице стоят пять домов.
Англичанин живет в красном доме.
У испанца есть собака.
В зеленом доме пьют кофе.
Датчанин пьет чай.
Зеленый дом стоит сразу справа от белого дома.
Тот, кто курит Old Gold, разводит улиток.
В желтом доме курят Kool.
В центральном доме пьют молоко.
Норвежец живет в первом доме.
Сосед того, кто курит Chesterfield, держит лису.
В доме по соседству с тем, в котором держат лошадь, курят Kool.
Тот, кто курит Lucky Strike, пьет апельсиновый сок.
Японец курит Parliament.
Норвежец живет рядом с синим домом.
Каждый из домов окрашен в свой цвет, в каждом доме живет представитель определенной национальности, у каждого — свой питомец, своя любимая марка сигарет и напиток.
