Алгоритм действий что это
Кто же ты такой, алгоритм?
Сегодня довольно легко столкнуться с недобросовестными школьными учебниками, в частности с учебниками по информатике. В главах, посвященных алгоритмам, вы можете найти непосредственно определение алгоритма. Не пояснение, о чем идет речь, не рассказ о предмете, а именно определение. Причем выделенное жирным шрифтом, старательно обведенное в рамку и помеченное какой-нибудь заметной пиктограммой в виде восклицательного знака. Обычно приправлено всё это соусом из кучи обязательных и необязательных свойств, образуя в итоге феерический кавардак. Давайте попытаемся понять, что же такое алгоритм, почему мы не может дать ему конкретного определения и выясним, какие свойства являются обязательными, а какие нет.
Составителей учебников легко понять, ведь на самом деле строгого определения алгоритма не существует, и более того, такого определения быть не может. Но вместо попыток объяснить, что к чему, авторы подсовывают бедным ученикам еще одно задание по зубрежке бесполезных и неправильных терминов. Чтобы не быть голословным, приведу выдержку из одного весьма распространенного учебника:
В университетах дела обстоят получше, однако автору этих строк на курсе по математической логике и теории алгоритмов пришлось столкнуться все с тем же винегретом из определения алгоритма и его свойств. Разберемся, что тут не так.
Бесконечность не предел
Такой же трюк с нумерацией не пройдет для бесконечных непериодических дробей (иррациональных чисел). Допустим такое множество счетное, то есть элементы этого множества можно пронумеровать натуральными числами. Тогда рассмотрим бесконечную десятичную дробь с нулевой целой частью, у которой первая цифра после запятой не равняется цифре на той же позиции у дроби с номером 1, вторая цифра не равняется цифре на второй позиции у дроби с номером 2 и т.д. Тогда полученная дробь будет заведомо отличаться от всех дробей хотя бы одной цифрой. Получается для нее не нашлось номера в нашей бесконечной нумерации! Примененная схема доказательства называется канторовским диагональным методом в честь придумавшего ее математика Георга Кантора.
Про бесконечные дроби
Не стоит делать ошибку, записывая в иррациональные числа все бесконечные дроби. Иррациональными являются только те числа, которые нельзя представить в виде несократимой дроби вида m/n. В десятичной системе счисления дроби 1/3 и 2/7 тоже окажутся бесконечными, однако их «бесконечность« обусловлена выбранной системой счисления. В системе счисления по основанию 21 эти дроби будут иметь конечное представление, а вот, например, дробь 1/2 окажется бесконечной (периодической).
Говорят, что множество бесконечных десятичных дробей имеет мощность континуум, которая обозначается символом ℵ1 (алеф-один). В дальнейшем нам понадобится следующее множество. Рассмотрим некоторый алфавит (конечное множество символов). Теперь представим множество всех конечных цепочек символов алфавита A*. Коль скоро алфавит конечен, и каждая цепочка конечна, то множество таких цепочек счетно (их можно пронумеровать натуральными числами).

Допустим в наш алфавит вошли все придуманные на земле символы: русский алфавит, японские иероглифы, шумерская клинопись и т.д. Тогда в наше множество войдут все написанные когда-либо книги, все книги, которые будут написаны и все книги, которые никто не стал бы писать (например, хаотичные последовательности символов). Кроме того, представим книгу, толщиной в Солнечную систему и диагональю листа равной диаметру Млечного Пути, набранную 12-м шрифтом. В наше придуманное множество войдут все такие книги, отличающиеся хотя бы одним символов, и не только они, ведь вселенная бесконечна! Кто мешает представить себе книгу, размером в миллиарды световых лет? А все такие книги? Уже на этом этапе воображение может давать сбои, а ведь наше множество всего лишь счетное. Чтобы дополнить множество до континуума, нужно рассмотреть бесконечную книгу, по сравнению с которой, предыдущие книги — детские игрушки. Но и одной бесконечной книги нам не хватит, нужно рассмотреть все бесконечные книги.
Конструктивно оперировать континуальными бесконечностями невозможно. Даже работая со счетными множествами, мы не рассматриваем сами множества, а только говорим, что какой бы не был элемент N, всегда найдется элемент N+1. Если мы ставим себе прикладную задачу, появление в наших рассуждениях континуальной бесконечности должно служить нам «тревожной лампочкой»: осторожно, выход за пределы конструктивного.
Алгоритмы и вычислимость
Компьютер проводит свои вычисления, подчиняясь некоторой программе, которая воплощает собой конструктивную процедуру, или алгоритм. Не сложно догадаться, что алгоритм как раз и есть то правило, по которому вычисляется функция. Можно сказать, функция считается вычислимой, если для нее существует некоторый алгоритм.
Понятия алгоритм и вычислимая функция оказываются настолько заковыристыми, что некоторые составители учебной литературы не утруждают себя попытками разъяснить их суть. Дело в том, что определения алгоритма не существует, и кроме того, существовать не может, иначе пришлось бы выбросить на свалку целый раздел математики — теорию вычислимости. Попробуем разобраться более подробнее.
Частично-рекурсивные функции и тезис Черча
Все началось с того, что математик Давид Гильберт в 1900 году предложил список нерешенных на тот момент математических проблем. Позже выяснилось, что десятая проблема (проблема решения произвольного диофантового уравнения) оказалось неразрешимой, но для доказательства этого факта пришлось составить целую новую математическую теорию. Вопросами того, какие задачи можно конструктивно решить, и что такое конструктивное решение, занялись математики Курт Гедель, Стивен Клини, Алонсо Черч и Алан Тьюринг.

Как выяснилось выше, континуальные бесконечности не всегда подходят под конструктивные рассуждения, поэтому Гедель и Клини предложили рассматривать только функции натурального аргумента (при необходимости любые функции над счетными множествами можно привести к «натуральным функция» путем замены элементов множеств их номерами). Изучая вычислимость таких функций, Гедель, Клини, Аккерман и другие математики пришли к так называемому классу частично-рекурсивных функций. В качестве определения этого класса рассматривается набор базовых, очень простых функций (константа, увеличение на единицу и проекция, которая сопоставляет функции многих аргументов один из ее аргументов) и операторов, позволяющих из функций строить новые функции (операторы композиции, примитивной рекурсии и минимизации). Слово «частичные» показывает, что эти функции определены лишь на некоторых числах. На остальных они не могут быть вычислены. Попытки расширить класс частично-рекурсивных функций ни к чему не привели, так как введение новых операций приводило к тому, что получалось множество функций, совпадающее с классом частично-рекурсивных. В дальнейшем Алонсо Черч отказался от попыток расширения этого класса, заявив, что, видимо:
Частично-рекурсивные функции соответствуют вычислимым функциям в любом разумном понимании вычислимости.
Это утверждение называют тезисом Черча. Стоит отметить, что тезис Черча не является теоремой или доказанным утверждением. Во-первых, не понятно, что такое «разумное понимание», во-вторых, превратив тезис Черча в доказанный факт, мы лишаем себя перспектив дальнейшего исследования вычислимости и механизмов вычислений. Никто, впрочем, не мешает попробовать определить такой набор операций, который был бы мощнее базиса для частично-рекурсивных функций. Только вот, до сих пор это никому не удавалось сделать.

Формальная теория алгоритмов во многом построена аналогично теории вычислимости. Считается, что алгоритм есть некое конструктивное преобразование входного слова (цепочки символов некоторого алфавита) в некоторое выходное слово. Опять же, здесь мы имеем с функциями вида A*->A*. Конечно, предложенное описание не подходит под определение алгоритма, так как неясно, что же такое «конструктивное преобразование». Хоть понятия алгоритма и вычислимой функции близки, не стоит их смешивать. Для одного и того же алгоритма может быть предъявлено сколько угодно его записей на каком-нибудь формальном языке, но соответствующая вычислимая функция всегда одна. Один из основателей формальной теории алгоритмов, Алан Тьюринг, предложил формальную модель автомата, известного как машина Тьюринга. Тезис Тьюринга гласит:
Каково бы не было разумное понимание алгоритма, любой алгоритм, соответствующий такому пониманию, может быть реализован на машине Тьюринга.
Любые попытки построить более мощные автомат заканчивались неудачей: для каждого такого автомата (машина Поста, нормальные алгоритмы Маркова, автоматы с регистрами и несколькими лентами) удавалось построить аналогичную машину Тьюринга. Некоторые ученые объединяют тезис Черча и тезис Тьюринга в тезис Черча-Тьюринга, так как они весьма близки по духу.

Таким образом, определив понятие алгоритма, мы будем вынуждены забыть о тезисе Черча-Тьюринга, и отказаться от целой математической теории, богатой содержанием и подарившую нам множество практических результатов.
Свойства алгоритмов
Мы выяснили, почему у алгоритма не может быть конкретного определения. Однако можно определить свойства, которыми должен обладать каждый алгоритм. К сожалению, в литературе часто смешивают обязательные и необязательный свойств. Разберемся подробнее.
Обязательные свойства
Начнем с обязательных свойств. Алгоритм можно записать в виде конечного текста из символов конечного алфавита. Действительно, бесконечный текст мы не можем записать чисто технически, а раз алгоритмы имеют отношение к конструктивной деятельности, бесконечными они быть не могут. Возможность представить алгоритм в виде конечного текста можно назвать свойством объективности и конечности.
Еще одно достаточно очевидное свойство любого алгоритма — его дискретность. Независимо от исполнителя, исполнение алгоритма представляет собой дискретный процесс, при рассмотрение распадающийся на элементарные действия. Понимать дискретность можно и в том смысле, что любая информация, над которой работает алгоритм может быть представлена в виде текста.
Третье фундаментальное свойство алгоритмов называется детерминированностью. Оно заключается в том, что следовать предписанной процедуре можно только одним способом. Единственное, что может повлиять на ход выполнения — это исходные данные, однако при одних и тех же исходных данных, алгоритм всегда выдает один и тот же результат.
Эти три свойства присущи всем алгоритмам. Если нарушено хотя бы одно из них, перед нами уже не алгоритм. С натяжкой к обязательным свойствам можно добавить понятность для исполнителя, хотя это уже на грани фола. По большей части. это относится не к самому алгоритму, а к его записи.

Необязательные свойства
Наряду с обязательными свойствами, алгоритм может обладать некоторыми частными свойствами, которые вовсе не обязательны. Начнем с массовости. Конечно, хочется, чтобы алгоритмы решали классы задач в зависимости от входных данных. Однако существуют алгоритмы, которые вообще не зависят от входных данных, например всем известный вывод на экран «Hello world». Как среди вычислимых функций существуют константные, так и среди алгоритмов существуют генераторы единственного результата.
Теперь рассмотрим широко распространенное убеждение, что алгоритмы должны обладать свойством правильности и завершаемости. Начнем с правильности. Такое свойство попросту невозможно формализовать, так как отсутствуют критерии этой правильности. Наверняка, многие из вас сталкивались с ситуацией, когда программист считает программу правильной, а заказчик нет. С завершаемостью дела обстоят интереснее. Рассмотрим термин «применимость« — алгоритм называется применимым к слову, если, получив на вход это слово, он завершается за конечное число шагов. Самое интересное то, что проблема применимости является алгоритмически неразрешимой, то есть невозможно составить алгоритм, которые определял бы по записи алгоритма и входному слову, завершится ли он за конечное число шагов. Никто не мешает вам составить программу, состоящую только из одного бесконечного цикла. И эта программа все еще будет алгоритмом.
Про зависающие программы
Программы, которые не могут зациклиться, на самом деле входят в класс примитивно-рекурсивных — подмножество частично-рекурсивного класса. Отличает их отсутствия оператора минимизации. Он то и вносит пикантности. Если вы используете «неарифметический цикл» while или рекурсию, для которых нельзя заранее определить, сколько раз они выполняться, то ваша программа сразу переходит из класса примитивно-рекурсивных в класс частично-рекурсивных.
Теперь перейдем к пресловутой последовательности шагов. Дело в том, что алгоритм может быть представлен в любой из имеющихся формальных систем (частично-рекурсивные функции, машина Тьюринга, лямбда-исчисление и т.д.). Воплощение алгоритма в виде компьютерной программы далеко не всегда будет описанием последовательности шагов. Здесь все зависит от парадигмы программирования. В императивной парадигме программисты действительно оперируют последовательностью действий. Однако существуют и другие парадигмы, такие как функциональная (привет Haskell программистам), где нету никаких действий, а лишь функции в сугубо математическом смысле, или чистая объектно-ориентированная, которая основана не на «последовательности действий», а на обмене сообщениями между абстрактными объектами.
Заключение
Иногда мир устроен несколько сложнее, чем хотелось бы. Существующие формализмы в теории алгоритмов не более чем абстрактные математические системы, наподобие геометрии Евклида или теории вероятности, тогда как понятие вычислимости, возможно, находится вне математики и является свойством нашей Вселенной наряду со скоростью света и законом всемирного тяготения. И хотя, скорее всего, нам так и не удастся ответить на вопрос, что такое алгоритмы и вычислимость, попытки найти ответ на этот вопрос оказались более ценными, чем возможный однозначный ответ.
Материал данной статьи во многом опирается на 1-ый том «Программирование: введение в профессию» А. В. Столярова. Тем, кто хочет подробнее изучить вопросы, связанные с алгоритмами и теорией вычислимости, кроме этой книги, советую Босс В «От Диофанта до Тьюринга» и трехтомник А. Шеня по математической логике и теории алгоритмов.
Дата-центр ITSOFT — размещение и аренда серверов и стоек в двух дата-центрах в Москве. За последние годы UPTIME 100%. Размещение GPU-ферм и ASIC-майнеров, аренда GPU-серверов, лицензии связи, SSL-сертификаты, администрирование серверов и поддержка сайтов.
Что такое Алгоритм простыми словами
Хотим мы этого или не хотим, но уже сегодня человечество живет наполовину в цифровом мире. Математика – Богиня нашего цифрового мира и Алгоритм – пророк ее.
Впрочем, алгоритмы властвуют над человеком практически с того момента, когда двуногое существо начало мыслить и планировать свои действия на шаг вперед, что и дало людям критическое преимущество в борьбе за существование перед животными, живущими инстинктами.
Однако, инстинкт тоже в своем роде является алгоритмом, а в чем же тогда преимущество человека?
Именно способность самостоятельно создавать подобные действия и является кардинальным отличием мыслящего человека от подвластного природным инстинктам животного.
Что называется алгоритмом
В математике и информатике под алгоритмом понимается порядок операций или набор инструкций, предназначенных для описания последовательности действий исполнителя в процессе выполнения практической задачи, приводящей к заранее известному результату.
Многие люди не догадываются, но с алгоритмами люди сталкиваются буквально на каждом шагу в своей обычной жизни. И даже более того, без них человек не смог бы и шагу ступить.
Наиболее знакомые людям алгоритмы – это бытовые привычки. По сути, личность человека – это набор привычек, то есть, постоянно повторяющихся действий привычного поведения.
Думаю вам такой порядок действий хорошо знаком.
В глобальном смысле вся жизнь человека подчинена пролонгированному решению – родился, получил образование, устроился на работу, женился, родил детей, воспитал, вышел на пенсию.
Аналогичным образом функционируют и компьютерные программы, только для вычислительной машины порядок операция кодируется в виде последовательности цифр, букв и символов.
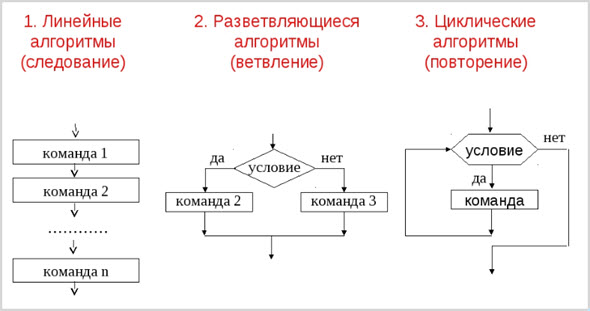
Понятно, что, чем сложнее порядок операций, приводящих к определенному результату, тем длиннее программа. Причем, алгоритм, то есть, порядок действий, не обязательно выглядит как линейна последовательность.
В зависимости от практической задачи структура алгоритма может изменяться.
Например, программа управления буром на нефтяной вышке. Пока грунт однообразный, бурение происходит в одном режиме. Если сверло натыкается на более твердую породу, происходит изменение режима бурения, для чего переключается программный алгоритм.
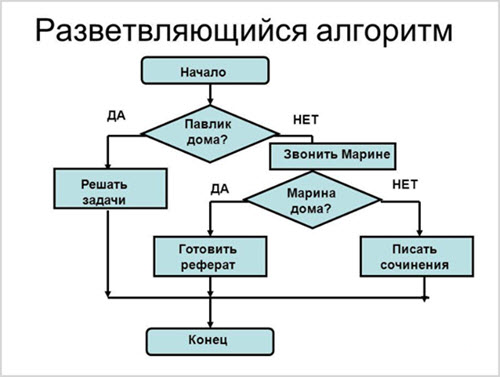
Жизнь человека – это тоже сложный разветвляющийся алгоритм. Пока мужчина холост – он живет по одному порядку, а когда женится – алгоритм (порядок жизни) мужчины кардинально меняется.
Здесь можно привести в пример работу повара в ресторане быстрого питания. Посетителе все как один заказывают гамбургеры. Повар, чтобы приготовить сотни гамбургеров, в течение рабочего дня повторяет одну и ту же последовательность операций. Открыл холодильник – вытащил полуфабрикат – поджарил котлету – разрезал булку – вложил котлету – добавил соус– закрыл булку.
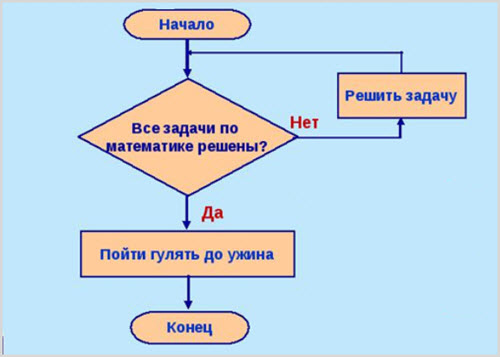
Циклические действия мы видим в человеческом обществе. В некотором смысле, большинство людей повторяют один и тот же цикл жизни на протяжении столетий. Кажется, в буддизме это называется «карма».
В практике программирования, в жизни, на производстве алгоритмы могут быть любой сложности, в сочетании всех трех описанных типов.
Мы начали наше исследование с того, что цифровизация изменила человеческую цивилизацию. А когда начали углубленно разбираться в математических решениях, неожиданно выяснилось – ничего не изменилось от начала времен. Люди всегда жили по строгим правилам. Даже те люди полностью во власти алгоритмов, которые и считать-то не умеют.
В каких сферах их применяют
Алгоритмы буквально пронизывают всю Вселенную. Сам термин «algorithm», как принято считать, происходит от имени средневекового арабского математика Аль-Хорезми.
В новой истории данное понятие стало известно широкой публике в середине 20-го века, когда в моду вошла кибернетика. Основные принципы компьютерной алгоритмики как раз и были разработаны где-то в 50-х – 60-х годах прошлого века, в том числе советскими учеными.
В каких сферах деятельности применяются алгоритмы? Проще назвать – где они не применяются. В практическом смысле их массовое применение есть в промышленном производстве и сфере обслуживания позволило сделать колоссальный рывок в благосостоянии человеческого общества.
Возьмите лист бумаги и последовательно запишите все действия, которые вы совершаете каждый день. Составьте такие списки действий на всю неделю. Скорее всего окажется, что с понедельника по пятницу у вас вполне такой циклический алгоритм, а в субботу происходит небольшое ответвление.
В течение дня вы выполняете ряд линейных алгоритмов, приводящих к заранее известным результатам (приготовление и прием пищи, стирка одежды, исполнение своих профессиональных обязанностей в офисе или цеху).
Кстати, автоматическая стиральная машинка тоже использует ряд циклических алгоритмов в зависимости от типа белья.
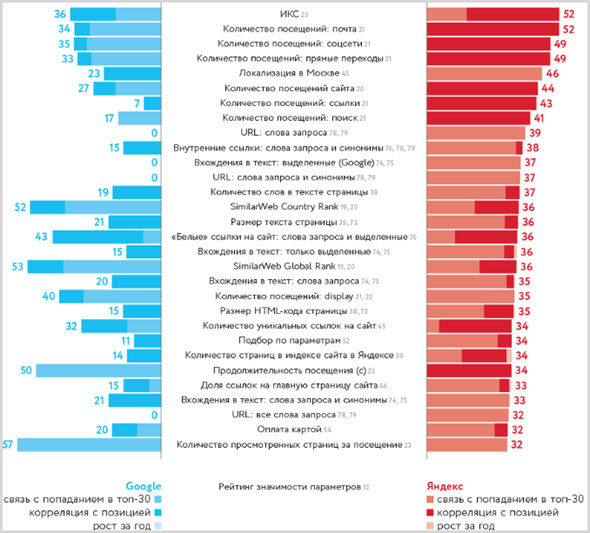
По каким алгоритмам работает поиск от Google и Яндекс
Яркий пример – работа поисковых сервисов. Как же Яндекс и Google могут так быстро находить на миллионах сайтов в интернете ответы практически на любой вопрос пользователя?
Как известно из инсайдерских кругов, поисковые системы используют порядка 1500 алгоритмов для того, чтобы пользователи могли быстро находить в интернете любую информацию.
На самом общем уровне можно выделить три глобальных алгоритма поисковых машин.
Многие пользователи полагают, что после запуска поиска по фразе Google со всех ног мечется по всему интернету и там ищет относящуюся к делу (релевантную) информацию.
Ничего подобного. Весь контент со всех веб-страниц заранее собирается специальными программами (которые тоже есть алгоритмы) – так называемыми поисковыми роботами.
Собранная информация хранится в Индексе поисковой машины – базе данных. Слово Index по-английски означает «каталог». Это примерно, как в обычной библиотеке все книги разделены по полкам, а в Каталоге лежат карточки с краткими описаниями. Индекс Яндекса – это и есть такой цифровой каталог всего интернет-контента.
Когда пользователь запускает поиск по определенному вопросу, в работу вступает алгоритм определения релевантности. Соответствие контента на сайте вопрос пользователя определяется до смешного просто – если в тексте присутствуют фразы, соответствующего поисковому запросу – такой контент признается релевантным и подготавливается к выдаче.
Фразы в тексте, соответствующие поисковому запросу принято называть «ключевыми словами» или «ключевиками».
Чтобы поисковой машине было легче найти контент на сайте, веб-мастера специально добавляют в текстовый контент соответствующие ключевые слова. Это называется «поисковая оптимизация».
После того, как алгоритм релевантности нашел в базе данных (индексе) весь контент, подходящий по теме поискового запроса, в работу включаются все те сотни и тысячи алгоритмов, предназначенные для определения качества и полезности контента.
Некоторые алгоритмы поисковых систем известны и имеют названия.
Зная, что некоторые недобросовестные веб-мастера порой идут на манипуляции, чтобы получить преимущества в поисковой выдаче, программисты Google и Яндекс разработали фильтры. С помощью фильтров поисковый компьютер выявляет «серые», недобросовестные способы оптимизации сайтов и «пессимизирует», понижает такие ресурсы в результатах поиска по запросу.
Чтобы не допустить недобросовестной оптимизации и манипуляций, поисковые компании сохраняют свои истинные алгоритмы в строжайшем секрете.
Так то, всё, что известно относительно алгоритмов Яндекса и Google веб-мастерам и специалистам по поисковому продвижению, найдено и выявлено чисто эмпирическим путем или относится к области гипотетических предположений.
Что такое алгоритм
Содержание
Вступление [ править ]
Геометрия развивает геометрическое мышление, математика — абстрактное математическое, логика — логическое, физика — физическое… А какое мышление развивает информатика? Информатика есть наука, служащая информационным технологиям. Но фундаментальными достижениями этой науки оказались не сами технологии, а общие методы построения систем и решения сложных задач. Базисом этих методов являются алгоритмы и системный подход к решению задач. Поэтому информатика развивает алгоритмическое мышление и учит системному подходу к решению задач.
Сегодня мы познакомимся с понятиями алгоритма и исполнителя. Оказывается, не так-то просто понять, чем определяется сущность алгоритма.
Понятие алгоритма [ править ]
Запись алгоритма на формальном языке называется программой. Иногда само понятие алгоритма отождествляется с его записью, так что слова «алгоритм» и «программа» — почти синонимы. Небольшое различие заключается в том, что под алгоритмом, как правило, понимают основную идею его построения. Программа же всегда связана с записью алгоритма на конкретном формальном языке.
Приведём для примера простой алгоритм действия пешехода, который позволит ему безопасно перейти улицу:
Алгоритмы обладают свойством детерминированности (определённости): каждый шаг и переход от шага к шагу должны быть точно определены так, чтобы его мог выполнить любой другой человек или механическое устройство.
Кроме детерминированности, алгоритмы также должны обладать свойством конечности и массовости:
Конечность Алгоритм всегда должен заканчиваться за конечное число шагов, но это число не ограничено сверху. Массовость Алгоритм применяется к некоторому классу входных данных (чисел, пар чисел, набору букв и тому подобному). Не имеет смысла строить алгоритм нахождения наибольшего общего делителя только для одной пары чисел 10 и 15.
Операция суммирования бесконечного ряда не является элементарной ни для современных компьютеров, ни для человека, а если разложить эту операцию на отдельные шаги сложения, то получим бесконечное число шагов. Алгоритмы же по определению должны выполняться за конечное число шагов и через конечное число шагов предоставлять результат вычислений.
Понятие элементарных объектов и элементарных действий [ править ]
| 0 | → 00000000 |
| 1 | → 00000001 |
| 2 | → 00000010 |
| 3 | → 00000011 |
| 4 | → 00000100 |
| 5 | → 00000101 |
| … | → … |
| 250 | → 11111010 |
| 251 | → 11111011 |
| 252 | → 11111100 |
| 253 | → 11111101 |
| 254 | → 11111110 |
| 255 | → 11111111 |
Указанный способ представления натуральных чисел в виде последовательности нулей и единиц называется двоичной записью числа. Каждому биту в этом представлении соответствует степень двойки. Самому правому биту соответствует 1 = 2 0 <\displaystyle 1=2^<0>> 


Конечный набор элементарных объектов может принимать лишь конечное число значений. Так, например, упорядоченный набор 8 бит (один байт) имеет 256 возможных значений. Из этого простого факта следует очень важное утверждение: среди команд исполнителя не может быть команд сложения или умножения произвольных натуральных (действительных) чисел.
При изучении языка программирования, вы встретитесь с таким явлением, как переполнение — ситуация, когда результат элементарной арифметической операции выходит за пределы подмножества чисел, которые можно записать в выбранном машинном представлении.
У каждого исполнителя есть конечный набор элементарных команд (действий), оперирующих элементарными объектами, которых также конечное число.
Входом алгоритма является конечный набор элементарных объектов. Во время работы алгоритма выполняется конечное число элементарных действий и результат алгоритма также является конечным набором элементарных объектов.
В компьютерах элементарным объектом является бит. Есть несколько стандартных способов записи чисел (действительных, целых, и целых неотрицательных) в виде последовательности бит фиксированной длины.
Алгоритм входным данным сопоставляет выходные данные и этим он чем-то похож на обыкновенную функцию. Но главной особенностью алгоритма является то, что он содержит описание того, как это сделать. Функция может быть задана неявно, а алгоритм — нет. Алгоритм описывает, что нужно сделать с входными данными, чтобы получить результат. При этом предполагается, что инструкции алгоритма выполняет исполнитель с ограниченными способностями: собственная память исполнителя конечна, также конечен и чётко зафиксирован набор инструкций, которые он может исполнять. В большинстве классических исполнителей присутствует внешняя память, которая в принципе не ограничена. Например у человека под рукой есть сколь угодно много листов бумаги, уложенных в бесконечный ряд (ячеек памяти), которые он может использовать. Заметьте, что информация о том, что на каком листке записано в какой-то момент может не поместиться в конечную память исполнителя и эту информацию ему также нужно будет записывать на листах.
Способы записи алгоритмов [ править ]
Алгоритмы можно описывать человеческим языком — словами. Так и в математике — все теоремы и утверждения можно записывать без специальных обозначений. Но специальный формальный язык записи утверждений сильно облегчает жизнь математикам: исчезает неоднозначность, появляются краткость и ясность изложения. Всё это позволяет математикам говорить и писать на одном языке и лучше понимать друг друга.
Большинство используемых в программировании алгоритмических языков имеют общие черты. В то же время, не всегда целесообразно пользоваться каким-либо конкретным языком программирования и загромождать изложение несущественными деталями. Здесь мы будем использовать псевдокод, который похож на язык Pascal, но не является таким строгим.
Разницу между программой и алгоритмом можно пояснить следующим образом. Алгоритм — это метод, схема решения какой-то задачи. А программа — это конкретная реализация алгоритма, которая может быть скомпилирована и выполнена на компьютере. Алгоритм, в свою очередь, является реализацией идеи решения. Это можно проиллюстрировать следующей схемой:
Идея решения → Алгоритм → Программа
Стрелка означает переход к следующему этапу решения задачи с повышением уровня подробности описания метода решения.
Алгоритм Евклида [ править ]
Запишем этот алгоритм с помощью псевдокода.
Псевдокод 1. Алгоритм Евклида
Инструкция return a означает «вернуть как результат вычислений объект a ».
Алгоритм вычисления чисел Фибоначчи [ править ]
В математике для описания функций часто используются рекуррентные соотношения, в которых значение функции определяется через её значение при других (обычно меньших) аргументах. Наиболее известным примером является последовательность Фибоначчи 1, 1, 2, 3, 5, 8, 13, …, определяемая следующими соотношениями:
Используя это рекуррентное соотношение, можно построить рекурсивный алгоритм вычисления чисел Фибоначчи:
Псевдокод 2. Числа Фибоначчи
Наибольший интерес в этом алгоритме представляет строчка 5:


На рисунке 1 изображено дерево рекурсивных вызовов, возникающее при вычислении F 6 <\displaystyle F_<6>> 






Для того, чтобы рекурсивный алгоритм заканчивал свою работу, необходимо, чтобы дерево рекурсивных вызовов при любых входных данных обрывалось и было конечным. В данном примере дерево рекурсивных вызовов обрывается на F 1 <\displaystyle F_<1>> 

Сколько раз вызывались вычисления F 2 <\displaystyle F_<2>> 








Но это не значит, что использовать рекурсию не надо. Рекурсия очень важный и удобный инструмент программирования. С помощью рекурсии успешно реализуют важный подход к решению задач: разделяй и властвуй.
Лучший способ решить сложную задачу — это разделить её на несколько простых и «разделаться» с ними по отдельности. По сути, это один из важных инструментов мышления при решении задач.
Псевдокод 3. Числа Фибоначчи: нерекурсивный алгоритм
От экспоненциального роста времени вычисления рекурсивных алгоритмов легко избавится с помощью запоминания вычисленных значений. А именно, в памяти хранят вычисленные значения, а в начале функции помещается проверка на то, что требуемое значение уже вычислено и хранится в памяти. Если это так, то это значение возвращается как результат, а вычисления и рекурсивные вызовы осуществляются лишь в том случае, когда функция с такими аргументами ещё ни разу не вызывалась. Подробнее этот метод мы рассмотрим при изучении динамического программирования.
Задача «Ханойские башни» [ править ]
Рассмотрим ещё один классический пример на рекурсивные алгоритмы — игру «Ханойские башни», придуманную ещё в 1883 году Эдуардом Люка. Есть три стержня и 64 кольца́, нанизанных на них. В начале все ко́льца находятся на первом стержне, причём все ко́льца разного диаметра, и меньшие ко́льца лежат на бо́льших. За ход разрешается взять верхнее кольцо с любого стержня и положить на другой стержень сверху, при этом запрещается класть большее кольцо на меньшее. Цель игры состоит в том, чтобы переместить всю пирамиду с первого стержня на второй.
Псевдокод 4. Ханойские башни
Задачу «Xанойские башни» можно значительно усложнить.
Дано четыре стержня. На одном из них 64 кольца́, размеры которых увеличиваются от верхнего к нижнему. Следуя правилам задачи «Ханойские башни» необходимо переместить их на второй стержень. Напишите программу, которая находит минимальное необходимое число операций перекладывания одного кольца́.
Примеры простых алгоритмических задач [ править ]
Здесь мы сформулируем несколько простых алгоритмических задач, которые полезно прорешать, чтобы освоится с понятием алгоритма.
Разработайте алгоритм вычисления числа F 1000 <\displaystyle F_<1000>> 
Дано множество прямых на плоскости, никакие три из которых не пересекаются в одной точке. Напишите рекурсивный алгоритм (псевдокод) закраски получившихся многоугольников в чёрный и белый цвета так, чтобы многоугольники одного цвета не имели общей стороны.
Рассмотрим следующее рекуррентное соотношение для функции f ( n ) = a n <\displaystyle 
Чем отличается алгоритм от функции?
Чем отличается программа от алгоритма?
В чём разница между идеей решения и алгоритмом решения задачи?