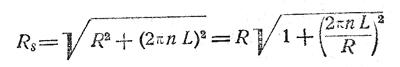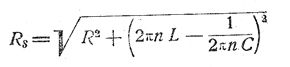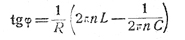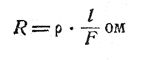Ампер умножить на ом что будет
Закон Ома: как связаны между собой напряжение, ток и сопротивление
Первая и, возможно, самая важная взаимосвязь между током, напряжением и сопротивлением называется законом Ома, который был открыт Георгом Симоном Омом и опубликован в его статье 1827 года «Гальваническая цепь, исследованная математически».
Напряжение, ток и сопротивление
Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.
Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.
Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.
Единицы измерения: вольт, ампер и ом
Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, нам нужно уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любые другие физические величины. Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. В таблице ниже приведены стандартные единицы измерения электрического тока, напряжения и сопротивления:
| Величина | Символ | Единица измерения | Сокращение единицы измерения |
|---|---|---|---|
| Ток | I | Ампер | А |
| Напряжение | V | Вольт | В |
| Сопротивление | R | Ом | Ом |
«Символ», присвоенный каждой величине, представляет собой стандартную букву латинского алфавита, используемую для представления этой величины в формулах. Подобные стандартизированные буквы распространены во всех физических и технических дисциплинах и признаны во всем мире. «Сокращение единицы измерения» для каждой величины представляет собой алфавитный символ(ы), используемый в качестве сокращенного обозначения конкретной единицы измерения.
Каждая единица измерения названа в честь известного экспериментатора в области электричества: ампер в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта, а ом в честь немца Георга Симона Ома.
Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя («Resistance» и «Voltage», соответственно), тогда как «I» для тока кажется немного странным. Предполагается, что буква «I» должна представлять «интенсивность» («Intensity»)(потока заряда). Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «I». Другой символ напряжения, «E», означает «электродвижущую силу» («Electromotive force»). Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах «E» зарезервировано для обозначения напряжения на источнике (таком как батарея или генератор), а «V»– для обозначения напряжения на любом другом элементе.
Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (так называемые «мгновенные» значения). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», тогда как пиковое напряжения при ударе молнии в тот самый момент, когда она попадает в линию электропередачи, скорее всего, будет обозначаться строчной буквой «е» (или строчной буквой «v»), чтобы отметить это значение как имеющееся в один момент времени. Это же соглашение о нижнем регистре справедливо и для тока: строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений в цепях постоянного тока, которые стабильны во времени, будут обозначаться заглавными буквами.
Кулон и электрический заряд
Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.
Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.
Формула закона Ома
Основное открытие Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, при любой заданной температуре прямо пропорциональна напряжению, приложенному к нему. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:
В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:
Анализ простых схем с помощью закона Ома
Давайте посмотрим, как эти формулы работают, чтобы помочь нам анализировать простые схемы:
Рисунок 1 – Пример простой схемы
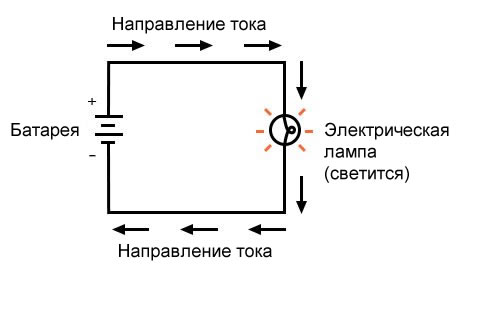
В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применить закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.
В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):
Рисунок 2 – Пример 1. Известны напряжение источника и сопротивление лампы
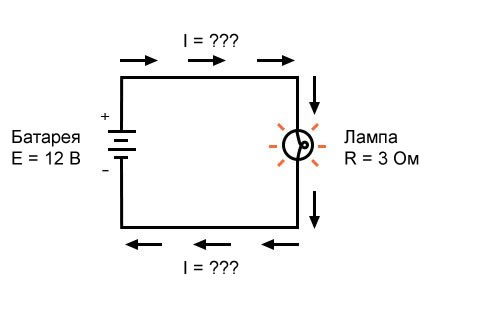
Какая величина тока (I) в этой цепи?
Во втором примере мы вычислим величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):
Рисунок 3 – Пример 2. Известны напряжение источника и ток в цепи
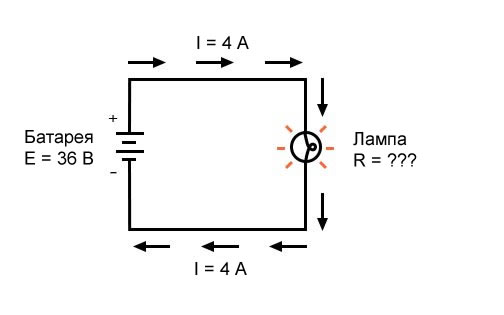
Какое сопротивление (R) оказывает лампа?
В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):
Рисунок 4 – Пример 3. Известны ток в цепи и сопротивление лампы
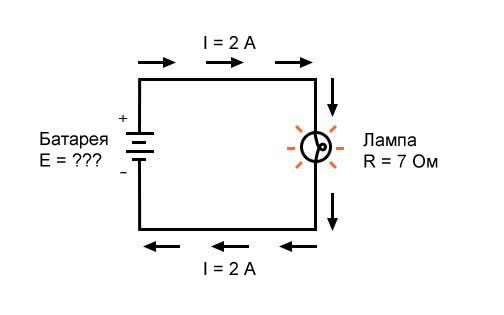
Какое напряжение обеспечивает батарея?
\[E = IR = (2 \ А)(7 \ Ом) = 14 \ В\]
Метода треугольника закона Ома
Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Рисунок 5 – Треугольник закона Ома
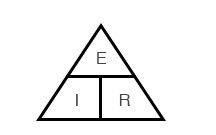
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:
Рисунок 6 – Закон Ома для определения R
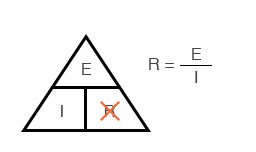
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:
Рисунок 7 – Закон Ома для определения I
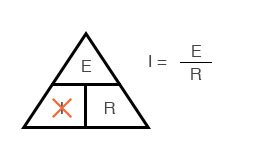
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:
Рисунок 8 – Закон Ома для определения E
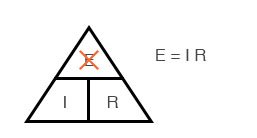
В конце концов, вам придется научиться работать с формулами, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!
Калькулятор Вт / Вольт / Ампер / Ом
Введите 2 значения, чтобы получить другие значения, и нажмите кнопку Рассчитать :
Расчет Ом
Сопротивление R в омах (Ом) равно напряжению V в вольтах (В), деленному на ток I в амперах (А):
Сопротивление R в омах (Ом) равно квадрату напряжения V в вольтах (В), деленному на мощность P в ваттах (Вт):
Сопротивление R в омах (Ом) равно мощности P в ваттах (Вт), деленной на квадрат тока I в амперах (A):
Расчет ампер
Ток I в амперах (A) равен напряжению V в вольтах (V), деленному на сопротивление R в омах (Ω):
Ток I в амперах (A) равен мощности P в ваттах (Вт), деленной на напряжение V в вольтах (В):
Ток I в амперах (A) равен квадратному корню из мощности P в ваттах (Вт), деленной на сопротивление R в омах (Ом):
Расчет вольт
Напряжение V в вольтах (В) равно току I в амперах (А), умноженному на сопротивление R в омах (Ом):
Напряжение V в вольтах (В) равно мощности P в ваттах (Вт), деленной на ток I в амперах (А):
Напряжение V в вольтах (В) равно квадратному корню из мощности P в ваттах (Вт), умноженной на сопротивление R в омах (Ом):
Расчет ватт
Мощность P в ваттах (Вт) равна напряжению V в вольтах (В), умноженному на ток I в амперах (A):
Мощность P в ваттах (Вт) равна квадрату напряжения V в вольтах (В), деленному на сопротивление R в омах (Ом):
Мощность P в ваттах (Вт) равна квадрату тока I в амперах (А), умноженному на сопротивление R в омах (Ом):
Электрические величины
Международный ом — сопротивление, оказываемое неизменяющемуся электрическому току при температуре тающего льда ртутным столбом, имеющим повсюду одинаковое поперечное сечение, длину 106,300 см и массу в 14,4521 г
0м подразделяется на 1 000 000 микромов
1000 000 омов составляют мегом
Ампер
Международный ампер — сила неизменяющегося электрического тока, который отлагает 0,00111800 г серебра в секунду, проходя через водный раствор азотно-кислого серебра.
Ампер подразделяется на 1 000 миллиампер или на 1 000 000 микроампер
Вольт
Международный вольт — электрическое напряжение, которое в проводнике, имеющем сопротивление в один ом, производит ток силою в 1 ампер.
Вольт подразделяется на 1 000 милливольт или на 1 000 000 микровольт
Международный ватт — мощность неизменяющегося электрического тока силою в 1 ампер при напряжении в 1 вольт.
1 000 ватт составляют киловатт
Кулон
Международный кулон (или ампер-секунда) — количество электричества, протекающее по проводнику в течение одной секунды при токе силою в 1 ампер.
3 600 кулонов составляют ампер-час
Джоуль
Ваттсекунда (международный джоуль) — работа, совершаемая электрическим током в течение 1 секунды при мощности тока в 1 ватт.
3 600 ваттсекунд составляют ваттчас, 100 ваттчасов составляют гектоваттчас, 1 000 ваттчасов составляют киловаттчас
Фарада
Международная фарада — емкость конденсатора, заряжаемого до напряжения в 1 вольт одним кулоном.
Фарада подразделяется на 1 000 000 микрофарад
Генри
Международный генри — самоиндукция цепи, в которой индуктируется напряжение в 1 вольт при изменении тока в этой цепи со скоростью 1 ампера в секунду.
Генри подразделяется на 1 000 миллигенри или на 1 000 000 микрогенри
При обычных практических электрических измерениях слово — «международный» в названиях электрических единиц может опускаться
Основные величины при переменном токе
Проводник, обладающий сопротивлением для постоянного тока R и самоиндукцией L, при переменном токе частоты n (n периодов или 2n перемен в секунду) имеет полное сопротивление
Если в цепи находится еще и емкость С, то полное сопротивление будет
Между током и приложенным напряжением имеется разность, фаз определяемая уравнением
Закон Ома для цепи переменного тока имеет форму J = E/Rs
Мощность в цепи переменного тока определяется выражением Е • I • cos Ψ; cos Ψ называется коэффициентом мощности
Если в цепи переменного тока 2πn • L = 1/2πn • C или (2πn) 2 L • C = 1, то Rs = R, то в такой цепи имеется резонанс, и для нее имеет силу простой закон Ома
Таблицы соотношений ампер, вольт, ватт, ом
Постоянный ток
| Вольты | Ватты : Амперы = Амперы х Омы = √ (Ватты х Омы) |
| Амперы | (Ватты : Вольты) = √(Ватты : Омы) = Вольты : Омы |
| Омы | Вольты : Амперы = Ватты : (Амперы) 2 = (Вольты) 2 : Ватты |
| Ватты | Амперы х Вольты = (Амперы) 2 х Омы = (Вольты) 2 : Омы |
Переменный ток
| Вольты | Ватты : (Амперы х cos Ψ) = Амперы х Омы х cos Ψ = √(Ватты х Омы) |
| Амперы | Ватты : (Вольты х cos Ψ) = 1/cos Ψ х √(Ватты : Омы) = Вольты : (Омы х cos Ψ) |
| Омы | Вольты : (Амперы х cos Ψ) = Ватты : (Амперы) 2 • cos 2 Ψ = (Вольты) 2 : Ватты |
| Ватты | Вольты х Амперы х cos Ψ = (Амперы) 2 х Омы х cos 2 Ψ = (Вольты) 2 : Омы |
Для cos Ψ можно брать в приблизительных подсчетах: для осветительных установок 0,85, для моторных установок 0,7
Электрическое сопротивление
т. е. проводник длиной в l метров и сечением F кв. миллиметров имеет сопротивление ρ • F/l омов
Здесь ρ — постоянная, зависящая от материала и температуры проводника — удельное сопротивление;
величина l/ρ — называется удельной электропроводностью
В таблицах помещены данные относительного сопротивления различных веществ, от величины которого зависит их пригодность в качестве проводников или изоляторов
Металлы для проводников
Сопротивление в омах на 1 м длины и 1 мм 2 сечения; при 20° С
| Алюминий | 0,029 | Ртуть | 0,058 |
| Алюминиевая бронза | 0,13 | Серебро | 0,016 |
| Бронза | 0,17 | Сталь мягкая | 0,1-0,2 |
| Железо | 0,086 | Сталь закаленная | 0,4-0,75 |
| Медь чистая | 0,017 | Свинец | 0,21 |
| Медь обыкновенная | 0,018 | Тантал | 0,12 |
| Никкель | 0,070 | Цинк | 0,06 |
| Платина | 0,107 |
Материалы для сопротивлений
| Графит | 4,0-12,0 | Кокс | 50 |
| Константин | 0,50 | Круппин | 0,85 |
| Манганин | 0,43 | Нейзильбер | 0,16-0,4 |
| Никкелин | 0,40 | Никкель | 0,34 |
| Реотан | 0,45 | Уголь | 60 |
Изолирующие материалы
Сопротивление в мегомах (1 мегом — 1000000 омов) куба в 1 см 3
| Кварц плавленный | 5.10 12 | Церезин | 5.10 12 |
| Парафин | 3.10 12 | Эбонит | 1.10 12 |
| Прессшпан | 1.10 5 | Каучук | 1.10 8 |
| Стекло | 5.10 7 | Сера | 1.10 11 |
| Черное дерево | 4.10 7 | Слюда белая | 3.10 10 |
| Линолеум | 1.10 7 | Янтарь | 5.10 10 |
| Тополь парафинированный | 5.10 5 | Клен парафинированный | 3.10 4 |
| Кварц перпендикулярно к оптической оси | 3.10 10 | Кварц параллельно к оптической оси | 1.10 |
| Шеллак | 1.10 10 | Целлулоид белый | 2.10 4 |
| Сургуч | 8.10 9 | Шифер | 1.10 2 |
| Воск желтый | 2.10 9 | Фибра красная | 5.10 2 |
| Фарфор неглазированный | 3.10 8 |
Жидкие сопротивления
Сопротивление в омах куба в 1 см 3 при 15° С
| Серная кислота 5% | 4,80 | Серная кислота 10% | 2,55 |
| Серная кислота 20% | 1,53 | Серная кислота 30% | 1,35 |
| Аммиак 1,6% | 15,22 | Аммиак 8,0% | 9,63 |
| Аммиак 16,2% | 15,82 | Раствор поваренной соли 5% | 14,92 |
| Раствор поваренной соли 10% | 8,27 | Раствор поваренной соли 15% | 6,10 |
| Раствор поваренной соли 20% | 5,11 | Раствор цинкового купороса 5% | 52,4 |
| Раствор цинкового купороса 10% | 31,2 | Раствор цинкового купороса 15% | 24,1 |
| Раствор цинкового купороса 20% | 21,3 | Раствор медного купороса 5% | 52,9 |
| Раствор медного купороса 10% | 31,3 | Раствор медного купороса 15% | 23,8 |
| Раствор сернокислого магния 5% | 83,0 | Раствор сернокислого магния 10% | 23,2 |
| Раствор сернокислого магния 15% | 20,8 | Раствор сернокислого магния 20% | 21,0 |
Сопротивление пробою
Переменный ток напряжением в 20 000 вольт пробивает изолирующий слой следующей толщины, мм:
Ампер умножить на ом что будет
Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.
В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.
Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению
Так записывается основная формула:
Путем преобразования основной формулы можно найти и другие две величины:
Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
Формула мгновенной электрической мощности:
Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.
Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.
Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.
Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.
Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.
Этот круг также, как и треугольник можно назвать магическим.