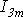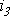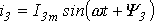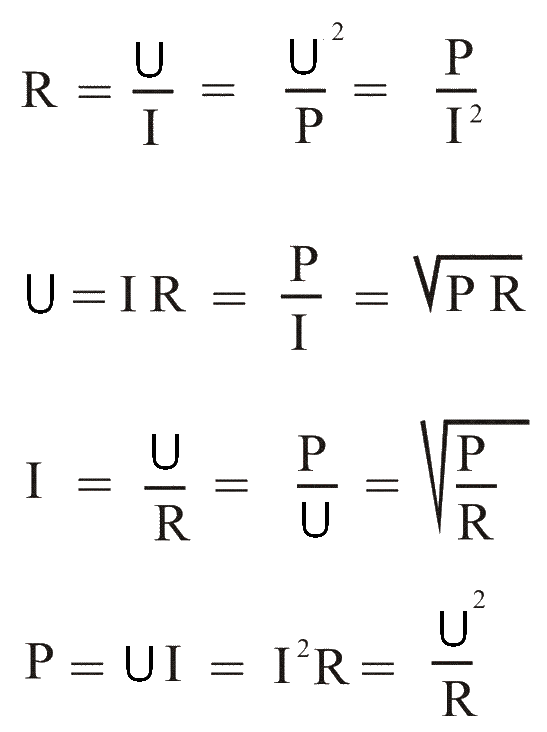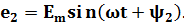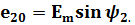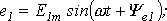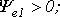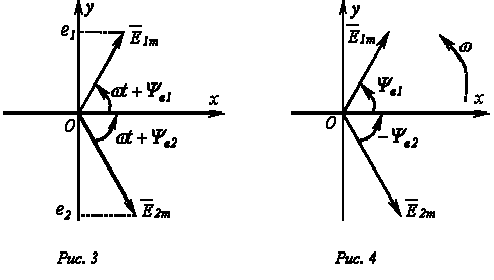Амплитудное значение эдс равно 380 в чему равно действующее значение эдс

Мгновенное значение эдс переменного тока для фазы 60 градусов равно 120 в, какова амплитуда эдс?

Мгновенное значение эдс переменного тока для фазы 60 градусов равно 120 в, какова амплитуда эдс?

Закон изменения ЭДС

$Em=120/( \frac < \sqrt<3>> <2>)=240/ \sqrt <3>=240 \sqrt <3>/3=80 \sqrt<3>V$ Ответ

$E=80 \sqrt <3>*sin100 \pi *0.25=80 \sqrt <3>sin25 \pi =0V$ Ответ.

Уравнение колебаний имеет вид I = 0, 28 sin 50 πt?

Уравнение колебаний имеет вид I = 0, 28 sin 50 πt.

Определить амплитуду, период и частоту колебаний.

Начертить график колебаний.

2. Мгновенное значение силы переменного тока частотой 50 Гц равна 2 А для фазы π / 4.

Определить амплитудное значение силы тока.

Найти мгновенное значение тока через 0, 015 с после начала периода.

Амплитудное значение ЭДС синусоидального тока, изменяющегося с частотой 50 Гц, равно 200 В?

Амплитудное значение ЭДС синусоидального тока, изменяющегося с частотой 50 Гц, равно 200 В.

Найдите мгновенное значение ЭДС через 0, 0025 с, считая от начала периода.

Фазуи и начальную ыфазу колебаний.

Мгновенное значение ЭДС задано выражением е = 100sin800пt?

Мгновенное значение ЭДС задано выражением е = 100sin800пt.

Найдите амплитуду, частоту, период, фазу и еачальную фазу колебаний.

Определите амплитуду, период частоту, фазу и начальную фазу колебаний ЭДС.

Электродвижущая сила индукции, возникающая в рамке при вращении ее в однородном магнитном поле, изменяется по закону е = 12sin100Пt?

Электродвижущая сила индукции, возникающая в рамке при вращении ее в однородном магнитном поле, изменяется по закону е = 12sin100Пt.

Определить : амплитудное значение ЭДС, действующее значение ЭДС, период и частоту тока, мгновенное значение ЭДС при t = 0, 01с.

Определите амплитуду, период частоту, фазу и начальную фазу колебаний ЭДС.

E = 100sin (50 л t) Определить : А) Амплетудное и действующее значения ЭДС ; Б)Частоту и период переменного тока В)Мгновенное значение ЭДС через о, 005 с?

E = 100sin (50 л t) Определить : А) Амплетудное и действующее значения ЭДС ; Б)Частоту и период переменного тока В)Мгновенное значение ЭДС через о, 005 с.

Определить действующее значение ЭДС, если амплитуда равна 380В?

Определить действующее значение ЭДС, если амплитуда равна 380В.

Дано N = 250МВт = 2, 5 * 10⁸Вт t = 10мин = 600с g = 10м / с² h = 12 5м Найти m N = A / t A = mgh N = mgh / t m = Nt / gh = 2, 5 * 10⁸Вт * 600с / (10м / с² * 125м) = 15 * 10¹⁰Вт * с / (1250м² / с²) = 1, 2 * 10⁸кг = 120 тыс. Т.

Решение на картинке во вложении.

1) Cилаиндукционноготокабольше тогда, когда большескоростьотносительногодвижениямагнитаикатушки. То есть прямая зависимость.

1) Нагреваем кастрюлю : Q₁ = c₁ * m₁Δ t = 880 * 0, 600 * 80≈ 42 000 Дж 2) Нагреваем воду : Q₂ = c₂ * m₂Δ t = 4200 * 4 * 80 = 1 334 000Дж 3) Общее количество теплоты : Q = Q₁ + Q₂ = 42 000 + 1 334 000 = 1 380 000 Дж = 1, 38 МДж.

60м÷12сек. = 5м / сек должен бежать Петя чтобы получить 5.

Источник

Определить действующее значение ЭДС, если амплитуда равна 380В?

Определить действующее значение ЭДС, если амплитуда равна 380В.

Амплитуда гармонических колебаний напряжения на конденсаторе равна 10 в?

Амплитуда гармонических колебаний напряжения на конденсаторе равна 10 в.

Чему равна действующее значение переменного напряжения.

Определите амплитуду ЭДС, частту и преиод её измены, а так же ЭДС в момент времени 0.

Мгновенное значение эдс переменного тока для фазы 60 градусов равно 120 в, какова амплитуда эдс?

Мгновенное значение эдс переменного тока для фазы 60 градусов равно 120 в, какова амплитуда эдс?

Действующие значение силы перемене оно тока 1А чему равна амплитуда силы тока в цепи?

Действующие значение силы перемене оно тока 1А чему равна амплитуда силы тока в цепи?

Фазуи и начальную ыфазу колебаний.

1. Определите частоту собственных колебаний в колебательном контуре, состоящем из конденсатора емкостью 2, 2 мкФ и катушки с индуктивностью 0, 65 мГн 2?

1. Определите частоту собственных колебаний в колебательном контуре, состоящем из конденсатора емкостью 2, 2 мкФ и катушки с индуктивностью 0, 65 мГн 2.

ЭДС индукции, возникающая в рамке при вращении в однородном магнитном поле, изменяется по закону e = 12sin 100пt B.

Возникающая в рамке ЭДС индукции при вращении в однородном магнитном поле изменяется по закону e = 12∙sin 100πt?

Возникающая в рамке ЭДС индукции при вращении в однородном магнитном поле изменяется по закону e = 12∙sin 100πt.

Определите амплитуду колебания ЭДС и ее действующее значение, а так же циклическую и линейную часоту колебаний, период, фазу и начальную фазу колебаний.

Электродвижущая сила индукции, возникающая в рамке при вращении ее в однородном магнитном поле, изменяется по закону е = 12sin100Пt?

Электродвижущая сила индукции, возникающая в рамке при вращении ее в однородном магнитном поле, изменяется по закону е = 12sin100Пt.

Определить : амплитудное значение ЭДС, действующее значение ЭДС, период и частоту тока, мгновенное значение ЭДС при t = 0, 01с.

E = 100sin (50 л t) Определить : А) Амплетудное и действующее значения ЭДС ; Б)Частоту и период переменного тока В)Мгновенное значение ЭДС через о, 005 с?

E = 100sin (50 л t) Определить : А) Амплетудное и действующее значения ЭДС ; Б)Частоту и период переменного тока В)Мгновенное значение ЭДС через о, 005 с.

Дано N = 250МВт = 2, 5 * 10⁸Вт t = 10мин = 600с g = 10м / с² h = 12 5м Найти m N = A / t A = mgh N = mgh / t m = Nt / gh = 2, 5 * 10⁸Вт * 600с / (10м / с² * 125м) = 15 * 10¹⁰Вт * с / (1250м² / с²) = 1, 2 * 10⁸кг = 120 тыс. Т.

Решение на картинке во вложении.

1) Cилаиндукционноготокабольше тогда, когда большескоростьотносительногодвижениямагнитаикатушки. То есть прямая зависимость.

1) Нагреваем кастрюлю : Q₁ = c₁ * m₁Δ t = 880 * 0, 600 * 80≈ 42 000 Дж 2) Нагреваем воду : Q₂ = c₂ * m₂Δ t = 4200 * 4 * 80 = 1 334 000Дж 3) Общее количество теплоты : Q = Q₁ + Q₂ = 42 000 + 1 334 000 = 1 380 000 Дж = 1, 38 МДж.

60м÷12сек. = 5м / сек должен бежать Петя чтобы получить 5.

Источник

Прописные истины для новичков.

Как рассчитать шунт для амперметра?
Почему, я намотал вторичную обмотку на 12 вольт, а блок питания у меня выдаёт 16 вольт?.
Как измерить, какую мощность выдаёт усилитель низкой частоты?
Такие вопросы порой часто возникают от новичков радиолюбителей. Кратко напомним им, чем нужно руководствоваться в своей практической деятельности.

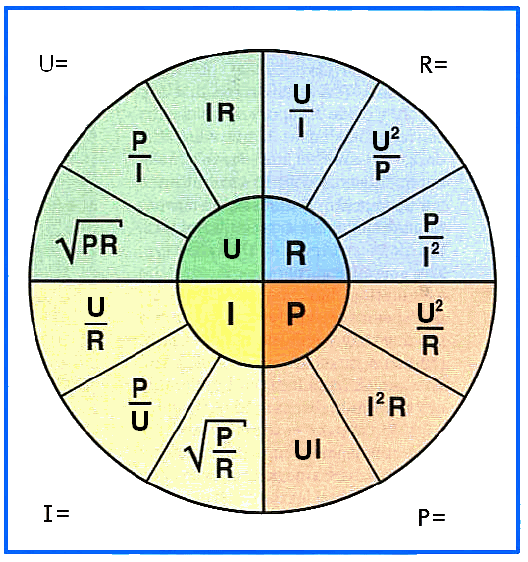
Закон Ома.

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка.

В этом треугольнике Ома, нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:

Электрические измерения.

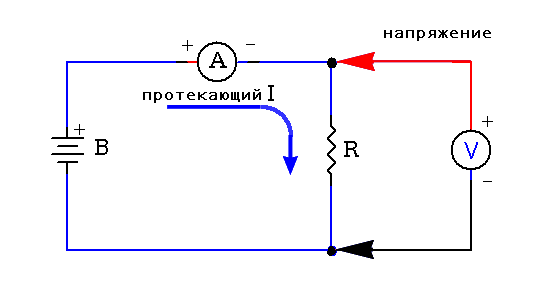
Нарисуем простейшую электрическую цепь, состоящую из батареи «В» и нагрузки «R», и рассмотрим, как необходимо измерять протекающий по цепи ток, и напряжение на нагрузке.

На рисунке выше показан порядок включения амперметра и вольтметра для измерения напряжения на нагрузке и протекающего через неё тока. Так же указана полярность подключения измерительных приборов в измеряемую цепь.

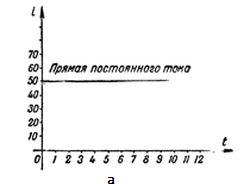
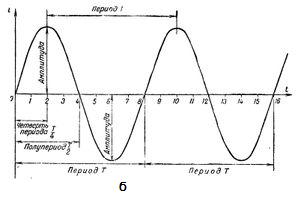
Постоянный и переменный ток.

На рисунке выше, на графиках изображены диаграммы постоянного (а), и переменного (б) тока.
Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом. Период обозначается буквой Т и измеряется в секундах.
Промежуток времени, на протяжении которого совершается половина полного цикла изменения тока, называется полупериодом. Следовательно, период изменения тока (ЭДС или напряжения) состоит из двух полупериодов. Совершенно очевидно, что все периоды одного и того же переменного тока равны между собой.
В течение одного периода своего изменения,ток дважды достигает максимального значения.
Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока.

Действующее (эффективное) и амплитудное значение переменного синусоидального тока (напряжения).

Все электроизмерительные приборы (амперметры, вольтметры), отградуированы для измерения действующего значения синусоидального тока или напряжения.

Все конденсаторы в выпрямительных фильтрах соответственно заряжаются до величины амплитудного значения.

Можно посчитать, что при действующем напряжении сети 220 В, амплитудное его значение будет составлять 310 вольт (220 помножить на 1,41).

Отсюда вытекает, что если собрать выпрямитель переменного действующего напряжения 220 вольт, то конденсаторы фильтра необходимо применять на рабочее напряжение не менее чем на 350 вольт, так как они заряжаются до амплитудного (максимального) значения переменного напряжения, а ещё лучше не менее 400 вольт, для обеспечения надёжности работы выпрямителя.

Ответим на вопросы в начале статьи;

Источник

Контрольная работа по физике на тему «Переменный ток» (11 класс)

А) Найдите частоту период и колебаний напряжения

5. Индуктивность катушки колебательного контура 50 мГн. Требуется настроить этот контур на частоту 0.5 МГц. Какова должна быть емкость конденсатора в этом контуре?

1. Запишите уравнение ЭДС. Если частота равна 50 Гц, а амплитудное значение ЭДС 150В

2. Чему равна емкость конденсатора, если переменному току частотой 50Гц он оказывает сопротивление 0,01 Ом

3. Найдите частоту колебаний в колебательном контуре, если индуктивность катушки 0,001 Гн, а емкость конденсатора 40 мкФ

4. Напряжение на зажимах вторичной обмотки трансформатора 50 В, сила тока во вторичной цепи 36 А. Первичная обмотка включена в цепь напряжением 220 В. Найдите силу тока в первичной обмотке трансформатора.

5. Катушку какой индуктивности нужно включить в колебательный контур, чтобы с конденсатором емкостью 2 мкФ получить электромагнитные колебания частотой 1к Гц?

2. Определите емкостное сопротивление конденсатора емкостью С=88 мФ, в цепи переменного тока частотой ν = 60 Гц.

3. В цепь последовательно подключены резистор сопротивлением 1 кОм, катушка индуктивностью 0,5 Гн и конденсатор емкостью 1 мкФ. Найти индуктивное, емкостное и полное сопротивление, если частота равна10 кГц.

4. Первичная обмотка трансформатора содержит 100 витков, а вторичная 1000 витков. Напряжение на первичной обмотке 120 В. Каково напряжение на вторичной обмотке?

2. Определите индуктивное сопротивление катушки, если ее индуктивность 4 Гн, а частота переменного тока 1000 Гц.

3. В цепи последовательно соединены резистор с сопротивлением 20 Ом, катушка индуктивностью 0,2 Гн, конденсатор емкостью 100 мкФ. Действующее напряжение составляет 75 В при частоте 50 Гц. Найти действующую силу тока в цепи.

4. Трансформатор, содержащий в первичной обмотке 840 витков, повышает напряжение с 220 В до 660 В. Каков коэффициент трансформации? Сколько витков содержится во вторичной обмотке?

2. Индуктивное сопротивление катушки в цепи переменного тока 50 Гц равно 31,4 Ом. Чему равна индуктивность катушки?

3. Найдите частоту собственных колебаний в контуре с индуктивностью катушки 10 мГн и емкостью конденсатора 1 мкФ

4. Сила тока в первичной обмотке трансформатора 0,5 А, напряжение на его концах 220 В. Сила тока во вторичной обмотке трансформатора 11 А, напряжение на его концах 9,5 В. Найти КПД трансформатора.

5. Индуктивность катушки колебательного контура 50 мГн. Требуется настроить этот контур на частоту 1 МГц. Какова должна быть емкость конденсатора в этом контуре?

1. По графику, изображенному на рисунке, определите амплитуду ЭДС, период тока и частоту. Запишите уравнение ЭДС.

2. Чему равна емкость конденсатора, если переменному току частотой 100 Гц он оказывает сопротивление 0,001 Ом

3. Найдите период колебаний в колебательном контуре, если индуктивность катушки 0,01 Гн, а емкость конденсатора 4 мкФ

4. Напряжение на зажимах вторичной обмотки трансформатора 60 В, сила тока во вторичной цепи 40 А. Первичная обмотка включена в цепь напряжением 240 В. Найдите силу тока в первичной обмотке трансформатора.

5. Катушку какой индуктивности нужно включить в колебательный контур, чтобы с конденсатором емкостью 2 мкФ получить электромагнитные колебания частотой 1000 Гц?

А) Найдите частоту период и колебаний напряжения

5. Индуктивность катушки колебательного контура 50 мГн. Требуется настроить этот контур на частоту 0,9 МГц. Какова должна быть емкость конденсатора в этом контуре?

1. Запишите уравнение ЭДС. Если частота равна 1050 Гц, а амплитудное значение ЭДС 380В

2. Чему равна емкость конденсатора, если переменному току частотой 500Гц он оказывает сопротивление 1 Ом

3. Найдите частоту колебаний в колебательном контуре, если индуктивность катушки 0,008 Гн, а емкость конденсатора 400 пкФ

4. Напряжение на зажимах вторичной обмотки трансформатора 850 В, сила тока во вторичной цепи 85 А. Первичная обмотка включена в цепь напряжением 220 В. Найдите силу тока в первичной обмотке трансформатора.

5. Катушку какой индуктивности нужно включить в колебательный контур, чтобы с конденсатором емкостью 2 нФ получить электромагнитные колебания частотой 5кГц?

5. Определите емкостное сопротивление конденсатора емкостью С=32 мкФ, в цепи переменного тока частотой ν = 50 Гц.

6. В цепь последовательно подключены резистор сопротивлением 10 кОм, катушка индуктивностью 5 Гн и конденсатор емкостью 21 мкФ. Найти индуктивное, емкостное и полное сопротивление, если частота равна10 кГц.

5. Первичная обмотка трансформатора содержит 1000 витков, а вторичная 10 витков. Напряжение на первичной обмотке 1120 В. Каково напряжение на вторичной обмотке?

6. Определите индуктивное сопротивление катушки, если ее индуктивность 44 Гн, а частота переменного тока 10040 Гц.

7. В цепи последовательно соединены резистор с сопротивлением 90 Ом, катушка индуктивностью 2 Гн, конденсатор емкостью 800 мкФ. Действующее напряжение составляет 110 В при частоте 50 Гц. Найти действующую силу тока в цепи.

8. Трансформатор, содержащий в первичной обмотке 8840 витков, повышает напряжение с 220 В до 6660 В. Каков коэффициент трансформации? Сколько витков содержится во вторичной обмотке?

2. Индуктивное сопротивление катушки в цепи переменного тока 100 Гц равно 31,4 Ом. Чему равна индуктивность катушки?

3. Найдите частоту собственных колебаний в контуре с индуктивностью катушки 10 мкГн и емкостью конденсатора 61 пФ

4. Сила тока в первичной обмотке трансформатора 0,2 А, напряжение на его концах 220 В. Сила тока во вторичной обмотке трансформатора 50 А, напряжение на его концах 0,5 В. Найти КПД трансформатора.

5. Индуктивность катушки колебательного контура 500 мГн. Требуется настроить этот контур на частоту 11 МГц. Какова должна быть емкость конденсатора в этом контуре?

1. По графику, изображенному на рисунке, определите амплитуду ЭДС, период тока и частоту. Запишите уравнение ЭДС.

2. Чему равна емкость конденсатора, если переменному току частотой 800 Гц он оказывает сопротивление 0,1 Ом

3. Найдите период колебаний в колебательном контуре, если индуктивность катушки 7 мГн, а емкость конденсатора 49 пФ

4. Напряжение на зажимах вторичной обмотки трансформатора 600 В, сила тока во вторичной цепи 90 А. Первичная обмотка включена в цепь напряжением 140 В. Найдите силу тока в первичной обмотке трансформатора.

5. Катушку какой индуктивности нужно включить в колебательный контур, чтобы с конденсатором емкостью 20 мФ получить электромагнитные колебания частотой 1800 Гц?

2. Определите индуктивное сопротивление катушки, если ее индуктивность 4 мГн, а частота переменного тока 1000 кГц.

3. В цепи последовательно соединены резистор с сопротивлением 500 Ом, катушка индуктивностью 2 Гн, конденсатор емкостью 800 мкФ. Действующее напряжение составляет 85 В при частоте 150 Гц. Найти действующую силу тока в цепи.

4. Трансформатор, содержащий в первичной обмотке 8400 витков, повышает напряжение с 220 В до 880 В. Каков коэффициент трансформации? Сколько витков содержится во вторичной обмотке?

1. Запишите уравнение ЭДС. Если частота равна 50 Гц, а амплитудное значение ЭДС 380В

2. Чему равна емкость конденсатора, если переменному току частотой 50Гц он оказывает сопротивление 80 Ом

3. Найдите частоту колебаний в колебательном контуре, если индуктивность катушки 91 мГн, а емкость конденсатора 90 мкФ

4. Напряжение на зажимах вторичной обмотки трансформатора 250 В, сила тока во вторичной цепи 80 А. Первичная обмотка включена в цепь напряжением 120 В. Найдите силу тока в первичной обмотке трансформатора.

5. Катушку какой индуктивности нужно включить в колебательный контур, чтобы с конденсатором емкостью 2 пФ получить электромагнитные колебания частотой 31кГц?

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник

ДОМОСТРОЙСантехника и строительство

Дать определения. Мгновенное, амплитудное, действующее и среднее значения ЭДС, напряжения, тока.

Что ты хочешь узнать?

Ответ

Проверено экспертом

Речь идём о переменном токе.

Мгновенное значение (ЭДС или напряжения или тока) — значение величины в данный момент времени. обозначается чаще всего маленькими буквами: e, u,i.

Амплитудное значение (ЭДС или напряжения или тока) — максимальное значение. Обозначается :

Действующее значение отличается от максимального тем, что оно меньше максимального в раз, т.е.( на примере тока, для напряжения и ЭДС аналогично):

Обозначается действующее значение или без иднекса или с индексом «д»:

Смысл действующего значения: при переменном токе (i) за период выделиться столько же тепла, сколько выделиться при действующем значении

Имеено действующее значение показывают приборы, подключённые в цепь с переменным током.

Максимальным значением (амплитудой) тока и напряжения называется та наибольшая величина, которой они достигают за один период. Максимальное значение тока и напряжения обозначается: напряжения — Um, тока — Im.

Величину переменной силы тока и напряжения для любого произвольного момента времени называют мгновенным значением этой величины. Обозначают мгновенные значения переменных величин строчными буквами латинского алфавита, например, электрического тока и электрического напряжения i и u соответственно.

Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.

Если ток изменяется по закону синуса, т. е.

,

то действующее значение переменного тока, обозначаемое также, как и значение постоянного тока заглавной буквой I латинского алфавита, определится как:

.

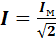
Аналогично для действующих значений синусоидальных напряжений:

.

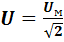
Фаза. Сдвиг фаз.

Пусть на якоре генератора укреплены два одинаковых витка 1 и 2, сдвинутых в пространстве на угол φ. При вращении якоря в витках наводится ЭДС индукции одинаковой частоты ω и амплитуды E_m, так как витки вращаются с одинаковой частотой в одном и том же магнитном поле.

Положение витков задано углами ψ₁ и ψ₂ для произвольного момента времени, которое можно считать t = 0. Мгновенные значения ЭДС как функции времени определяются выражениями:

;

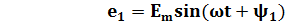
Следовательно, в момент t = 0 значения обеих этих ЭДС отличны от нуля:

;

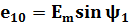
Электрические углы ψ₁ и ψ₂ характеризуют значения ЭДС в начальный момент времени и называются начальными фазами.

Сдвиг фаз — это разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.

Дата добавления: 2016-05-25 ; просмотров: 7354 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

,

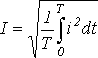
Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е₁ и е₂ соответствуют уравнения:

.

Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t=0): и —начальной фазой ( ).

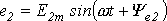
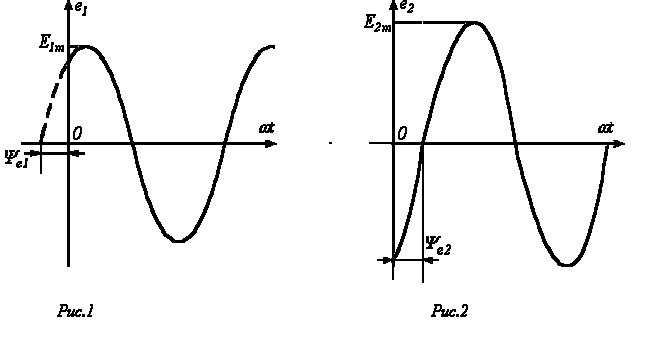
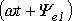
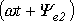
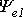
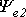
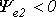
Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.

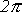
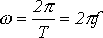
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.

.

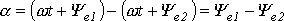
Векторное изображение синусоидально изменяющихся величин

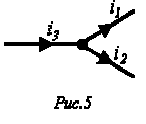
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е₁ и е₂ (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

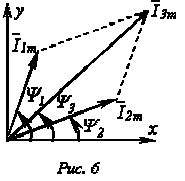
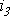
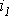
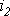
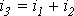
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:

.

Каждый из этих токов синусоидален и может быть представлен уравнением

и.

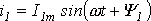
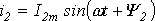
Результирующий ток также будет синусоидален:

.

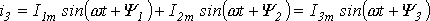
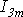
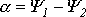
Определение амплитудыи начальной фазыэтого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt=0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

.

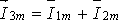
Построение векторной диаграммы в масштабе позволяет определить значения ииз диаграммы, после чего может быть записано решение для мгновенного значенияпутем формального учета угловой частоты:.

Источник