формула герона для каких треугольников
Что можно вычислить по формуле Герона
Формула Герона
Формула Герона носит такое название в честь греческого математика и инженера Герона Александрийского. Он жил в I веке нашей эры. Герон занимался механикой, оптикой, геометрией и гидростатикой. Учёный интересовался треугольниками с целочисленными сторонами и целочисленными площадями. Такие фигуры получили название Героновых треугольников.
Формулировка теоремы Герона
Формула Герона – это арифметическая формула для вычисления площади треугольника по длинам его сторон. В таком случае площадь равна корню из произведения разностей полупериметра и каждой из его сторон.
Формула и доказательство
Формула Герона выглядит следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
где S – это площадь треугольника; a, b, c – это стороны треугольника; p – это полупериметр треугольника.
Чтобы вычислять полупериметр, нужно пользоваться формулой:
Приведем доказательство.
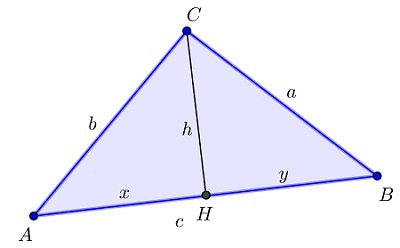
Для этого рассмотрим треугольник ABC.
CH – высота треугольника.
По теореме Пифагора из треугольников ACH и BCH получаем:
Найдем высоту треугольника.
С помощью этих равенств найдем высоту.
Для каких треугольников действует теорема
Применение формулы Герона допустимо для треугольников, у которых известны длины всех их сторон.
Примеры решения задач
Задача 1
Рассчитать площадь треугольника, если a=6, b=8, c=6.
Решение
Тогда площадь треугольника равна:
Задача 2
Вычислить площадь параллелограмма, если одна из его сторон равна 51, а диагонали равны 40 и 74.
Решение
Диагонали AC и BD пересекаются в точке O.
Если AD = 51, AC = 40 и BD = 74, то AO = 20, OD = 37.
Задача 3
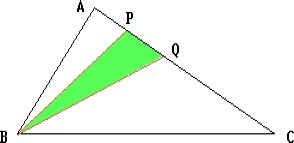
В треугольнике ABC три стороны: AB = 26, BC = 30 и AC = 28. Найти часть площади этого треугольника, заключённую между высотой и биссектрисой, проведёнными из вершины B.
Решение
BP и BQ – высота и биссектриса треугольника.
По свойству биссектрисы треугольника:
По теореме Пифагора из треугольника APB получаем:
Следовательно, \(PQ = AQ – AP = 13 – 10 = 3\)
Формула Герона для треугольника
В данной публикации мы рассмотрим формулу Герона, пользуясь которой можно найти площадь треугольника. Также разберем примеры решения задач для того, чтобы закрепить представленный материал.
Формула площади
Площадь треугольника ( S ) равняется квадратному корню из произведения его полупериметра ( p ) на разности полупериметра и каждой из его сторон ( a, b, c ).
Полупериметр ( p ) вычисляется таким образом:
Примечание: для использования формулы необходимо знать/найти длину всех сторон треугольника.
Формула получила такое название в честь греческого математика и механика Герона Александрийского, который изучал треугольники с целочисленными сторонами и площадью (героновские). К таким, например, относится прямоугольный треугольник с соотношением сторон 3:4:5, который также называют египетским.
Примеры задач
Задание 1
Найдите площадь треугольника со сторонами 6, 8 и 10 см.
Решение
Для начала найдем полупериметр:
p = (6 + 8 + 10) / 2 = 12 см.
Задание 2
В прямоугольном треугольнике длина гипотенузы равняется 15 см, а одного из катетов – 9 см. Вычислите площадь фигуры.
Полупериметр треугольника равен:
p = (9 + 12 + 15) / 2 = 18 см.
Формула Герона.
Формула Герона позволяет определить площадь треугольника (S) из его сторон a, b, c.
Чтобы вычислить площадь треугольника ∆ABC, если известны длины его сторон a, b и c, используют формулу Герона:
где p — полупериметр треугольника:

Рассмотрим нахождение площади треугольника с помощью формулы Герона:
Есть треугольник со сторонами a = 5, b = 6, c = 7. Вычислим полупериметр:
Далее подставляем данные в формулу для определения площади:
Формула Герона, доказательство.
В нем: CH — высота треугольника ABC, которая проведена из вершины C, |CH|=h, |AH|=x, |BH|=y.
Тогда c=x+y, и из теоремы Пифагора из треугольников ACH и BCH имеем:
Учитывая, что x+y=c, получаем 

Складываем последнее равенство с равенством y+x=c, получаем:
Далее находим высоту h треугольника:
Подставляем эти выражения в определенное выражение для h 2 :
Учитываем то, что 
Как найти площадь любого треугольника по трём сторонам
Часто бывает необходимо вычислить площадь той или иной геометрической фигуры. Если дело обстоит с прямоугольником или квадратом, то тут все более-менее ясно: формулы для их площадей интуитивно просты и понятны, а также легко запоминаются. Но как быть, если речь идет о каком-нибудь треугольнике, для вычисления площади которого простого перемножения сторон недостаточно. Тогда на помощь приходит она, госпожа Математика…
Что такое треугольник и какие бывают треугольники?
Вспомним определение из школьного курса геометрии: «Треугольником АВС называется фигура, состоящая из трех точек, не лежащих на одной прямой, и соединенных между собой отрезками». Точки А, В и С будут вершинами, а отрезки АВ, ВС и АС — сторонами треугольника. Треугольник АВС кратко записывают так: ∆ABC.
Треугольники бывают правильные, когда все их стороны равны. По-другому их еще называют равносторонними. Также есть равнобедренные, когда только две стороны одинаковы, и прямоугольные, когда один из углов — прямой.
Вычисление площади треугольника по трем сторонам. Формула Герона
Можно долго описывать свойства биссектрисы или медианы треугольника, однако, у нас другая задача: можно ли, зная длины всех сторон ∆АВС, найти его площадь? Такая необходимость возникает, если мы измерили три стороны треугольника, а углы нам неизвестны. Конечно, можно. Уже в I веке нашей эры была известна замечательная формула, позволяющая без проблем находить площади любых треугольников только по трем сторонам.
Эта формула, ныне известная как формула Герона (по имени древнегреческого ученого Герона Александрийского, жившего в I веке н. э., в чьей книге под названием «Метрика» эту формулу и обнаружили), была открыта знаменитым Архимедом. Она очень проста и сводится к следующему:
Площадь любого треугольника ABC со сторонами a, b и с определяется формулой Герона:
S=√p (p-a)(p-b)(p-c), где p=(a+b+c)/2 — полупериметр ∆ABC.
Как получить формулу Герона?
Как же была получена столь замечательная формула? Все очень просто. Если вы запасетесь небольшим терпением, то сами сможете убедиться, как же легко можно прийти к формуле Герона. Для этого поднимите из памяти на свет вашего разума известные со школьной скамьи теоремы синусов и косинусов. Как они звучат?
Теорема синусов: «Отношения сторон ∆ABC к синусам противолежащих им углов равны:
a/sin α=b/sin β=c/sin γ, где α, β и γ — углы ∆АВС, противолежащие сторонам а, b и с соответственно».
Теорема косинусов: «Квадрат стороны ∆ABC равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: a²=b²+c²-2bc•cos α».
Используя их, вы сами придете к желаемому результату, как это сделал много веков назад знаменитый математик. Вот вам небольшая подсказка: используйте формулу площади ∆ABC подвум сторонам и углу между ними. Удачи!
Вариации формулы Герона
Существуют и другие формы записи этой формулы. Вот они:
Еще формулы для вычисления площади треугольника:
Примеры
Эти примеры помогут вам лучше освоить тему:
Пример №1
Вычислить площадь ∆АВС, если a=10, в=20, c=30. Решение. Находим полупериметр: p=(10+20+30)/2=30. Теперь по формуле Герона: S=√(30•(30−10)•(30−20)•(30−30))=0, т. е. на самом деле мы имеем дело не с треугольником, а с отрезком, у которого с=а+b=10+20=30.
Пусть а=3, в=5, c=6, тогда p=(3+5+6)/2=7. Искомая площадь S=√(7•(7−3)•(7−5)•(7−6))=√(7•4•2•1)=√56≈7,48.
Пример №2
Найти угол γ между сторонами треугольника a и в из предыдущей задачи. Решение. S=(aв/2)•sin γ, sin γ=2S/(aв)=2•√56/(3•5)=0,99778, γ=arcsin 0,99778≈86°.
Пример №3
Пусть даны координаты вершин ∆ABC: А (1,2), В (-1,3), С (2,-5). Найти его площадь по одной из формул. Решение. Находим длины его сторон: AB=√((-1−1)²+(3−2)²)=√5, BC=√((2-(-1))²+(-5−3)²)=√73, AC=√((2−1)²+(-5−2)²)=√50. Тогда S=¼•√(4•5•73-(5+73−50)²)=¼•√676=26/4=6,5.
Пример №4
Периметр равностороннего треугольника численно равен его площади. Чему равна его сторона а? Решение. Так как периметр равностороннего треугольника равен Р=3а, а его площадь S=¼•a²√3, то приравняв эти равенства, получим: 3а=¼•а²√3. Решив это уравнение, найдем: а=4√3.
Пример №5
Площадь круга радиусом R равна площади равностороннего ∆ABC. Найти радиус круга. Решение. Площадь круга S=πR² по условию задачи равна площади равностороннего ∆ABC: πR²=¼•а²√3. Из этого соотношения находим: R=а√(√3)/(2√π)≈0,3713а.
Пример №6
Сторона и два прилежащих к ней угла в ∆ABC равны соответственно а=7, β=30°, γ=60°. Чему равна его площадь? Решение. S=½•7²/(ctg 30°+ctg 60°)=(49/2)/(√3+1/√3)=49√3/8≈10,61.
Видео
Это видео поможет вам закрепить материал, изложенный в статье.
Как найти площадь треугольника
Основные понятия
Треугольник — это геометрическая фигура, которая получилось из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере плоскости, ограниченной замкнутой геометрической фигурой.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Общая формула
1. Площадь треугольника через две стороны и угол между ними.
2. Площадь треугольника через основание и высоту.
S = 0,5 * a * h, где a — основание, h — высота.
3. Площадь треугольника через описанную окружность и стороны.
S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны.
S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.
Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:
S = r * p, где p — полупериметр.
5. Площадь треугольника по стороне и двум прилежащим углам.
S = a 2 : 2 * (sin(α)⋅sin(β)) : sin(180 — (α + β)), где a — сторона, α и β — прилежащие углы, γ — противолежащий угол.
6. Формула Герона для вычисления площади треугольника.
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
S = √ p * (p − a) * (p − b) * (p − c), где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам.
S = 0,5 * a * b, где a, b — стороны.
Площадь треугольника по гипотенузе и острому углу.
S = 0,25 * c 2 * sin(2α), где c — гипотенуза, α — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу.
S = 0,5 * a 2 * tg(α), где a — катет, α — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и по радиусу вписанной окружности.
S = r * (r + c), где c — гипотенуза, r — радиус вписанной окружности.
Площадь треугольника вписанного в окружность.
Площадь прямого треугольника по формуле Герона.
S = (p − a) * (p − b), где a, b — катеты, p — полупериметр, который рассчитывается по формуле p = (a + b + c) : 2.
Для равнобедренного треугольника
Поиск площади через основание и сторону.
Вычисление площади через основание и угол.
S = 0,5 * a * b * sin(α), где a — боковая сторона, b — основание, α — угол между основанием и стороной.
Вычисление площади через основание и высоту.
S = 0,5 * b * h, где b — основание, h — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними.
S = 0,5 * a 2 * sin(α), где a — боковая сторона, α — угол между боковыми сторонами.
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами.
S = b 2 : (4 * tgα/2), где b — основание, α — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности.
S = (3 * √ 3 * R 2 ) : 4, где R — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности.
Площадь равностороннего треугольника через сторону.
S = (√ 3 * a 2 ) : 4, где a — сторона.
Площадь равностороннего треугольника через высоту.
S = h 2 : √ 3, где h — высота.
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.