Как искать дискриминант квадратного уравнения

Все формулы связанные с дискриминантом

Дискриминант квадратного уравнения – это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.

Вид уравнения	Формула корней	Формула дискриминанта
ax 2 + bx + c = 0		b 2 – 4ac
ax 2 + 2kx + c = 0		k 2 – ac
x 2 + px + q = 0
		p 2 – 4q

Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:

Вид уравнения	Формула
ax 2 + bx + c = 0	, где D = b 2 – 4ac
ax 2 + 2kx + c = 0	, где D = k 2 – ac
x 2 + px + q = 0	, где D =
	, где D = p 2 – 4q

Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:

Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:

так как она относится к формуле:

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.

Решение квадратных уравнений через дискриминант

Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.

Пример 1. Решить уравнение:

Определим, чему равны коэффициенты:

Определим, чему равны коэффициенты:

D = b 2 – 4ac = (-6) 2 – 4 · 1 · 9 = 36 – 36 = 0, D = 0

Уравнение имеет всего один корень:

Определим, чему равны коэффициенты:

D = b 2 – 4ac = (-4) 2 – 4 · 1 · (-5) = 16 + 20 = 36, D > 0

Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Теорема Виета.

Квадратным уравнением называется уравнение вида

,

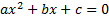
a,b,c – постоянные (числовые) коэффициенты.

В общем случае решение квадратных уравнений сводится к нахождению дискриминанта:

Формула дискриминанта: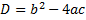

.

О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :

Мы уже разобрали, как решать квадратные уравнения. Теперь давайте более подробно рассмотрим, что называют дискриминантом квадратного уравнения.

Вернемся к нашей формуле для нахожденя корней квадратного уравнения.

Выражение « b 2 − 4ac », которое находится под корнем, принято называть дискриминантом и обозначать буквой « D ».

По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:

По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».

В зависимости от знака « D » (дискриминанта) квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.

I случай
D > 0
(дискриминант больше нуля)

x1 =

−5 + 9

4

x₂ =

−144x₁ = 1x₂ = −3

24x₁ = 1x₂ = −3

II случай
D = 0
(дискриминант равен нулю)

D = b 2 − 4ac
D = (−8) 2 − 4 · 16 · 1
D = 64 − 64
D = 0

III случай
D
(дискриминант меньше нуля)

D = b 2 − 4ac
D = (−6) 2 − 4 · 9 · 2
D = 36 − 72
D = −36
D

Ответ: нет действительных корней

Источник

Решение квадратных уравнений: формула корней, примеры

В продолжение темы «Решение уравнений» материал данной статьи познакомит вас с квадратными уравнениями.

Рассмотрим все подробно: суть и запись квадратного уравнения, зададим сопутствующие термины, разберем схему решения неполных и полных уравнений, познакомимся с формулой корней и дискриминантом, установим связи между корнями и коэффициентами, ну и конечно приведем наглядное решение практических примеров.

Квадратное уравнение, его виды

Зачастую квадратные уравнения также носят название уравнений второй степени, поскольку по сути квадратное уравнение есть алгебраическое уравнение второй степени.

Приведенные и неприведенные квадратные уравнения

По значению первого коэффициента квадратные уравнения подразделяют на приведенные и неприведенные.

Любое неприведенное квадратное уравнение возможно преобразовать в приведенное уравнение, если разделить обе его части на первый коэффициент (равносильное преобразование). Преобразованное уравнение будет иметь такие же корни, как и заданное неприведенное уравнение или так же не иметь корней вовсе.

Рассмотрение конкретного примера позволит нам наглядно продемонстрировать выполнение перехода от неприведенного квадратного уравнения к приведенному.

Задано уравнение 6 · x 2 + 18 · x − 7 = 0 . Необходимо преобразовать исходное уравнение в приведенную форму.

Решение

Полные и неполные квадратные уравнения

В случае же, когда коэффициенты b и c равны нулю (что возможно, как по отдельности, так и совместно), квадратное уравнение носит название неполного.

Полное квадратное уравнение – квадратное уравнение, в котором все числовые коэффициенты не равны нулю.

Порассуждаем, почему типам квадратных уравнений даны именно такие названия.

Решение неполных квадратных уравнений

Заданное выше определение дает возможность выделить следующие виды неполных квадратных уравнений:

Рассмотрим последовательно решение каждого вида неполного квадратного уравнения.

Решение уравнения a·x 2 =0

Кратко решение оформляется так:

Решение уравнения a · x 2 + c = 0

Резюмируем все рассуждения выше.

Решение

Ответ: уравнение 9 · x 2 + 7 = 0 не имеет корней.

Решение

Решение уравнения a·x 2 +b·x=0

Закрепим материал примером.

Решение

Кратко решение уравнения запишем так:

Дискриминант, формула корней квадратного уравнения

Для нахождения решения квадратных уравнений существует формула корней:

Нелишним будет понимать, как была выведена указанная формула и каким образом ее применять.

Вывод формулы корней квадратного уравнения

Вновь сформулируем выводы:

Так, результатом наших рассуждений стало выведение формулы корней квадратного уравнения:

Данные формулы дают возможность при дискриминанте больше нуля определить оба действительных корня. Когда дискриминант равен нулю, применение обеих формул даст один и тот же корень, как единственное решение квадратного уравнения. В случае, когда дискриминант отрицателен, попытавшись использовать формулу корня квадратного уравнения, мы столкнемся с необходимостью извлечь квадратный корень из отрицательного числа, что выведет нас за рамки действительных чисел. При отрицательном дискриминанте у квадратного уравнения не будет действительных корней, но возможна пара комплексно сопряженных корней, определяемых теми же полученными нами формулами корней.

Алгоритм решения квадратных уравнений по формулам корней

Решить квадратное уравнение возможно, сразу задействуя формулу корней, но в основном так поступают при необходимости найти комплексные корни.

В основной же массе случаев обычно подразумевается поиск не комплексных, а действительных корней квадратного уравнения. Тогда оптимально перед тем, как использовать формулы корней квадратного уравнения, сначала определить дискриминант и удостовериться, что он не является отрицательным (в ином случае сделаем вывод, что у уравнения нет действительных корней), а после приступить к вычислению значения корней.

Рассуждения выше дают возможность сформулировать алгоритм решения квадратного уравнения.

Примеры решения квадратных уравнений

Приведем решение примеров при различных значениях дискриминанта.

Решение

Решение

Необходимо решить уравнение 5 · y 2 + 6 · y + 2 = 0

Решение

В случае, когда стоит задача указать комплексные корни, применим формулу корней, выполняя действия с комплексными числами:

В школьной программе стандартно нет требования искать комплексные корни, поэтому, если в ходе решения дискриминант определен как отрицательный, сразу записывается ответ, что действительных корней нет.

Формула корней для четных вторых коэффициентов

Пусть выражение n 2 − a · c будет обозначено как D 1 (иногда его обозначают D ‘ ). Тогда формула корней рассматриваемого квадратного уравнения со вторым коэффициентом 2 · n примет вид:

Решение

Возможно было бы произвести вычисления и по обычной формуле корней квадратного уравнения, но в таком случае решение было бы более громоздким.

Упрощение вида квадратных уравнений

Иногда существует возможность оптимизировать вид исходного уравнения, что позволит упростить процесс вычисления корней.

Такое преобразование возможно, когда коэффициенты квадратного уравнения не являются взаимно простыми числами. Тогда обычно осуществляют деление обеих частей уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Связь между корнями и коэффициентами

Самыми известными и применимыми являются формулы теоремы Виета:

Также можно найти ряд прочих связей между корнями и коэффициентами квадратного уравнения. Например, сумма квадратов корней квадратного уравнения может быть выражена через коэффициенты:

Источник

Квадратные уравнения. Дискриминант. Решение, примеры.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )

Виды квадратных уравнений

Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.

Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:

В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.

Такие квадратные уравнения называются полными.

А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:

И так далее. Если же c = 0, получим уравнение без свободного члена:

И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:

Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.

Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе.

Вот и все главные виды квадратных уравнений. Полные и неполные.

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:

Формула для нахождения корней квадратного уравнения выглядит так:

Пример практически решён:

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Самые распространённые ошибки – путаница со знаками значений a, b и с. Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте!

Предположим, надо вот такой примерчик решить:

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится. Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

Узнали?) Да! Это неполные квадратные уравнения.

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с.

Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х₁ = 0, х₂ = 4.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

Дискриминант. Формула дискриминанта.

Волшебное слово дискриминант! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:

Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D. Формула дискриминанта:

И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют. Буквы и буквы.

Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых. Но, в упрощённом варианте, принято говорить об одном решении.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с. Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…

Приём первый. Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает? Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Источник

Общие сведения

Решение квадратных уравнений — одно из ключевых моментов в математике. Ещё древние вавилоняне и греки пытались найти закономерности при решении таких равенств. Но первым, кто описал методы нахождения дополнением квадрата, был индийский философ Будхаяма. Именно он предложил записывать уравнения в виде: ax 2 = c и ax 2 + bx = c. В дальнейшем способы усовершенствовались. Так, Евклид предложил метод геометрического вычисления ответа.

Но наиболее значимым стало открытие Буля. Изучая формулы различных уравнений, он пришёл к выводу, что выражения почти всегда можно упростить, заменив переменные другим набором, содержащим новые неизвестные. При этом, найдя их, определить первоначальные уже не составляет труда.

Такой способ был применён и к квадратному уравнению. Благодаря ему стало возможным упростить квадратичную форму с двумя переменными, используя дискриминант. Это понятие тесно связано с многочленом, имеющим следующий вид: d (m) = a 0 *m n + a 1 *m n-1 + a 2 *m n-2 + … + a n-1 *m + a n, где m — искомое неизвестное, a n, a n-1, a n-2, … a 1 и a 0 — числовые постоянные.

Термин «дискриминант» был придуман не математиками, но успешно стал ими использоваться при вычислении квадратичных функций. Произошёл он от латинского слова discriminans, что в дословном переводе означает «разделяющий». Важной величиной стало значение, придуманное Булем и имеющее вид b2 — 4ac. Учёный открыл, что после того как переменные линейно изменятся, дискриминант будет равняться первоначальному, умноженному на член, находимому из функции поведения неизвестных.

При решении равенств, содержащих формулу дискриминанта и его корней, используют формулу для быстрого определения количества возможных решений и их числового нахождения. Математически определение записывают следующим образом: p (x) = m + mx + ⋯ + mx, m ≠ 0, где: D (p) = m∏(m − m). То есть дискриминантом многочлена p (x) является сумма произведений корней на неизвестный коэффициент в основном поле их существования.

Смысл дискриминанта

Дискриминант — одно из эффективных решений квадратных выражений. С его помощью легко можно выявить, сколько корней имеет уравнение или установить, что их нет. Применять его можно как к полным квадратным равенствам, так и неполным. Но всё же во втором случае использовать дискриминант не нужно.

Эта тема изучается в седьмом и восьмом классе средней школы. Лучше понять смысл параметра поможет простой пример. Пусть имеется уравнение вида m 2 + 2m — 8 = 0. Не имея понятие о дискриминанте, решение уравнения сводится к приведению его к формуле квадрата суммы m 2 + 2m +1 — 1- 8 = 0. Добавление и вычитание единицы возможно, так как в итоге получается сложение с нулём.

В общем виде все эти преобразования можно выполнить в следующей последовательности:

Многочлен b2 — 4ac было решено принять за дискриминант. Это выражение по сути и определяет возможность существования решений и количество корней. Выполнив его расчёт, фактически и находится ответ уравнения.

Взаимосвязь параметра

Объяснение дискриминанта имеет и графическое обоснование. Физически задача заключается в комплексном подходе установления взаимосвязи. Фактически это фиксирование нулей параболы уравнения, то есть точек, в которой она пересекает ось абсциссы. Знак при переменной в квадрате будет определять положение веток параболы. Они будут идти вверх при a > 0, и вниз, если a 2 — 4 ac к удвоенному произведению первого коэффициента в уравнениях x1 = (- b + √ b 2 — 4 ac) / 2a; x2 = (- b — √ b 2 — 4 ac) / 2a. Подкоренное выражение называют формулой сокращённого дискриминанта.

Дискриминант при нахождении корней уравнения может принимать три значения:

Последнее выражение является формулой корней квадратного уравнения. Именно с её помощью могут решаться равенства, в степени которых стоит двойка. Через дискриминант можно вычислять корни и уравнений больших порядков. Для этого используются приёмы понижения степени до квадратного. Но эти операции учащиеся начинают изучать на уроках в выпускном классе, когда проходят решение уравнений n-го порядка.

Типовые примеры

Даже зная правило поиска корней через дискриминант, научиться быстро вычислять корни уравнения не получится, если не практиковаться. Поэтому решение практических задач обязательно входит школьную в программу обучения:

Определить возможность решения уравнения 4m 2 — 2m — 3 = 2. Для приведения к удобному виду двойку нужно перенести влево. В итоге получится 4m 2 — 2m — 5 =0. Дискриминант равняется: D = 4 — 4 * 4 * (-5) = 4 + 80 = 84. Так как он больше нуля, то корней будет два. Тут сложность заключается в том, что нет целого числа, которое равнялось бы корню из √84. Однако, √84 = √4 * √21 = 2 √21. Используя формулы, получаем что m = (2 ± 2√21) / 2 * 4. Двойку можно вынести в числителе за скобки, получив тем самым удобную запись: m = (2 * (1 ±√21) / 2 * 4 = (1 ± √21) / 4. Это выражение и есть искомое решение.

Таким образом, любое выражение нужно стремиться переписать так, чтобы оно приняло классический вид. Это может быть умножение или деление на какое-либо число, поиск общего знаменателя. А уже после нужно искать дискриминант, по виду которого можно определить, есть ли смысл в дальнейшем нахождении корней уравнения.

Вычисления на онлайн-калькуляторе

Поиск решений уравнения через дискриминант — довольно простая тема. Необходимо запомнить всего две формулы и свойства, зависящие от значения дискриминанта. Но на практике попадаются примеры содержащие интегралы, логарифмы, экспоненциальные функции. При этом всё это может быть записано в виде сложных дробей.

Решая задания самостоятельно, даже имея большой опыт и знания, есть вероятность допущения ошибки. Поэтому при вычислении сложных примеров стоит использовать онлайн-калькуляторы.

Из сервисов, предлагающих такие услуги, можно отметить:

Эти российские сайты. Их интерфейс интуитивно понятен. Для выполнения вычислений не нужно указывать персональные данные или платить за услуги. От пользователя лишь требуется записать в предложенную форму квадратное уравнение или даже матрицу, состоящую из них. Программа автоматически выполнит нужный расчёт и предоставит пошаговое решение. Кроме того, на сайтах решателей уравнений содержится в кратком виде теоретический материал и типовые примеры с подробным решением.

Даже ничего не понимающий в дискриминантах человек, воспользовавшись онлайн-калькулятором несколько раз, сможет восполнить пробелы в знаниях, самостоятельно научиться решать примеры, узнает, как правильно должен писаться дискриминант. Использование онлайн-сайтов для математических решений позволяет сэкономить время и получить точный результат.

Источник