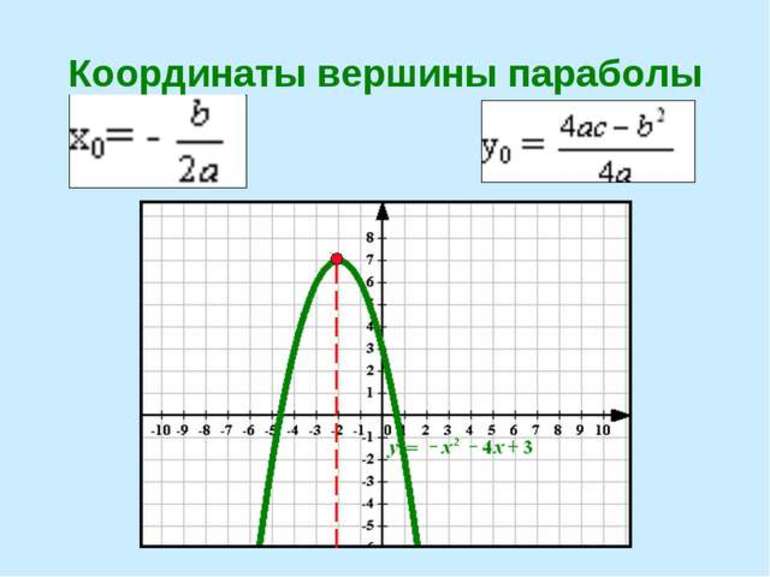
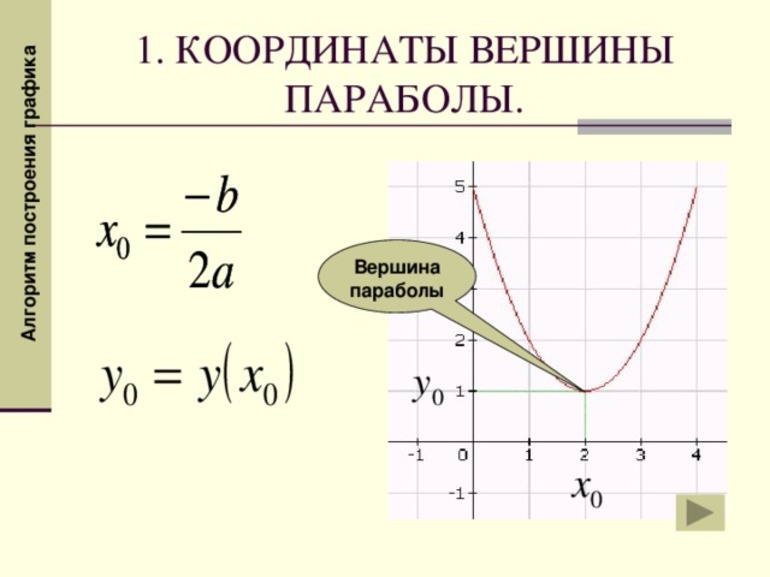
Как искать вершину параболы формула
Квадратичная функция. Построение параболы
8 класс, 9 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
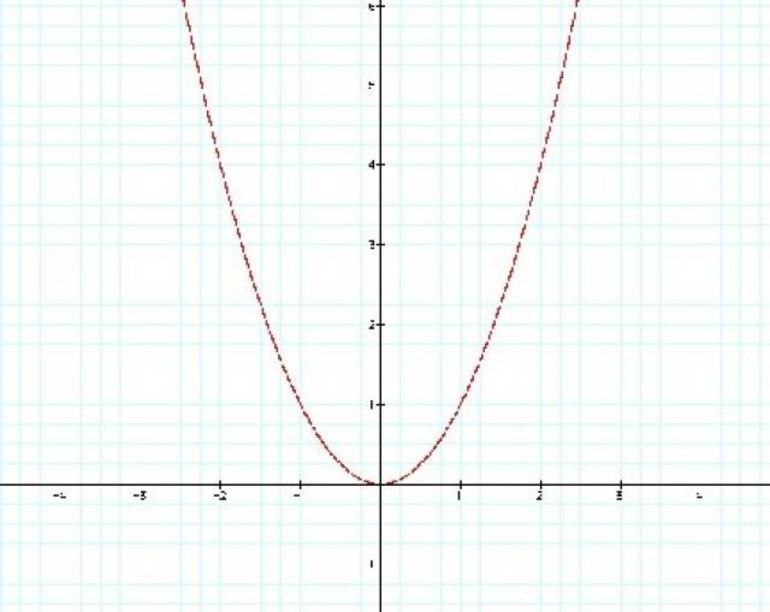
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
Рассмотрим три случая:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Как строим:
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
Как строим:
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.
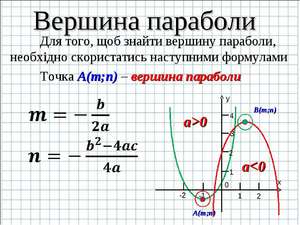
Как найти вершину параболы: три формулы
Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.
Нахождение вершины параболы: способы, примеры, советы
У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.
Первый способ
Например, y =x 2 –8 x +15;
находим первый, второй коэффициенты и свободный член;
подставляем значения a и b в формулу;
вычисляем значения y;
Значит, вершина находится в точке (4;-1).
Рассмотрим на примере y =x 2 –6x+5
1) Приравниваем к нулю:
2) Находим дискриминант, используя формулу: D = b 2 –4 ac:
3) Находим корни уравнения по формуле (-b±√ D)/2a:
Второй способ
Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.
2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.
У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:
3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.
4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).
Третий способ
Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:
1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.
2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.
Рассмотрим этот способ подробнее.
Дана функция y = 4x²+16x-17;
f'(x) = (4x²+16x-17)’ = 8x+16 =0
Построение параболы
Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.
2) Заполняем таблицу
Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Советы
Правильно находите коэффициенты.
Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.
Делайте всё поэтапно. Следуйте алгоритму.
Обратите ваше внимание на то, что:
Видео
Это видео поможет вам научиться находить вершину параболы
Вершина параболы
Что такое вершина параболы
Вершина параболы — это точка, в которой наблюдается пересечение параболой оси координат и ее невозможность держать направление выше или ниже в координатной плоскости.
Чтобы найти ВП, необходимо применить формулу:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Исходя из координат, можно узнать расположение вершины параболы и построить ее.
Вывод формулы координат вершины параболы
Рассматриваемую формулу используют для решения квадратных уравнений, которые имеют вид:
Ее график представляет собой параболу, формулу которой мы определили выше. Но не всегда требуется пользоваться данной формулой, так как сначала можно найти значение х, а затем подставить его в уравнение и найти y.
Для того, чтобы вывести формулу ВП, нужно преобразовать квадратную функцию к виду:
Делают это с помощью метода выделения полного квадрата, то есть \(\left(a+b\right)^2\) преобразуют в \(a^2+2ab+b^2.\)
Функции вида \(y\;=\;f(x\;+\;l)\;+\;m\) отличаются от \(y\;=\;f(x)\) сдвигом из графиков по оси абсцисс на –l и по оси ординат на m. l в переписанной квадратичной функции равняется:
Получается, что l и m — это координаты x0 и y0.
Как найти координаты, основные способы
Существует несколько способов нахождения координат ВП:
Примеры решения задач
Найти вершину параболы для уравнения: \(y=x^2-5x+7.\)
Найти ВП для уравнения: y=5(x-1)(x+7).
Решение: Ищем нули функции: 5(x-1)(x+7)=0. Тогда x-1=0 либо x+7=0. Из этого x=1; x=-7.
Парабола, график, вершина, нули.
теория по математике 📈 функции
Функция вида y=ax 2 +bx+c, где а, b, с – некоторые числа, причем, а ≠ 0 число, х – переменная, называется квадратичной функцией.
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.
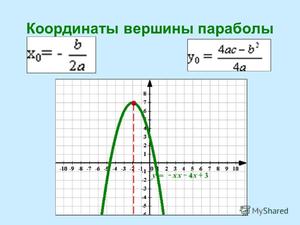
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax 2 +bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х 2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2 ∙ 2 2 – 8 ∙ 2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х 2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х 2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
D=b 2 – 4ac=4 2 — 4 ∙ 1 ∙ ( − 5 ) = 36
Значит, нули функции равны –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3
Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.
Теперь можно выполнить соответствие:
Пример №4
Рассмотрим еще пример на соответствие
В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0.
Итак, найдем х0 для формулы «Б»:
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
А) a>0, с >0 Б) а 0 В) а>0, с
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a 0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с 0, с >0 — это график №1
Б) а 0 — это график №3
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х 2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
Из всего вышеперечисленного можно найти ответ:
pазбирался: Даниил Романович | обсудить разбор | оценить
Общие сведения
Парабола — кривая, состоящая из равноудаленных точек от заданной точки (вершина) и прямой. Последняя называется директрисой. График функции имеет ось симметрии, которая проходит по определенной траектории и зависит от функции кривой (рис. 1). Ее вершина находится в центре координат.
Рисунок 1. График квадратичной функции с вершиной в начале координат.
Однако существуют и другие случаи прохождения кривой. Она может пересекать оси абсцисс или ординат. В некоторых случаях ее ветви направлены вниз. При вращении вокруг оси симметрии получается поверхность, которая используется в различных устройствах. По этому принципу изготовлены фары автомобиля, зеркала в телескопах и т. д. Кроме того, парабола — это квадратичная зависимость переменных друг от друга. Парабола имеет некоторые свойства:
Следует отметить, что оптическое свойство — это способность отражать свет от источника. Если пучок лучей, которые являются параллельными ее оси, отражаются в параболе, то они собираются в фокусе кривой. При нахождении источника света в фокусе происходит отражение параллельного пучка лучей относительно ее оси.
Уравнения квадратичной функции
Параболу можно описать несколькими способами. Каждый из них нужно применять в конкретных случаях для удобства вычислений. Существует три формы описания кривой:
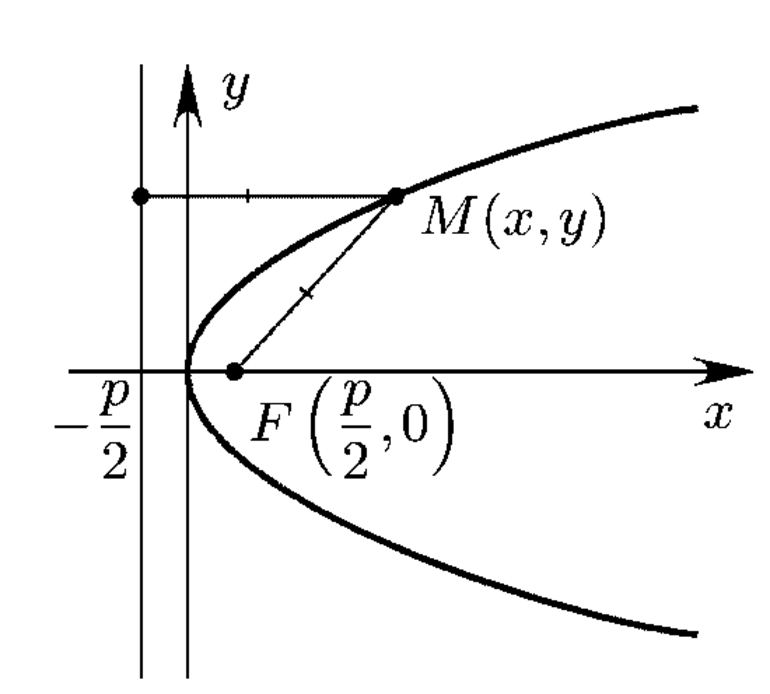
В первой форме она имеет следующий вид: y 2 = 2px. Если поменять местами оси декартовой системы, то получится следующий вид: x 2 = 2yp. Коэффициент p — фокальный параметр. Он соответствует расстоянию между фокусом и директрисой. Кроме того, его значение всегда больше нуля. Вершина лежит всегда между фокусом и директрисой кривой на расстоянии, равном p/2 (рис. 2).
Рисунок 2. Директриса и фокус.
Пусть уравнение директрисы (прямая, которая параллельна оси ОУ) имеет следующий вид: х + p/2 = 0. Координаты фокуса F — (р/2;0). Начало координат делит луч, проходящий из точки F и точки пересечения с директрисой на 2 равных отрезка. Величина FM рассчитывается таким образом: FM = [(x — p/2)^2 + y 2 ]^0.5. Отрезок (луч) из точки М до директрисы равен p/2 + x. Если приравнять оба выражения, то равенство имеет такой вид: p/2 + x = [(x — p/2)^2 + y 2 ]^0.5. При возведении в квадрат и приведении подобных слагаемых, получается искомое уравнение параболы (y 2 = 2px).
В последней формуле переменная D является дискриминантом квадратного уравнения искомой функции. Он вычисляется с помощью такого соотношения: D = b 2 — 4ac. При а>0 фокус лежит на оси, и находится над вершиной. Ось симметрии параллельна оси ординат. Кроме того, она проходит через вершину кривой. Расстояние до нее равно ¼ величины «а». Если а 2 + Bxy + Cy 2 + Dx + Ey + F = 0. Дискриминант равен нулю (при старших членах).
В полярной системе координат с осями p и v уравнение квадратичной функции имеет такой вид: p (1 + cos (v)) = p. Расстояние от фокуса до директрисы обозначается фокальным коэффициентом p. Кроме того, p соответствует удвоенной длине отрезка, проведенного от фокуса до вершины.
Методы нахождения вершины
Когда функция представлена неполным квадратом, нужно прибавить или отнять одинаковое число к двум частям уравнения. Если воспользоваться этим методом, то можно вычислить сразу значения х и у. Алгоритм нахождения вершины для функции у = x 2 + 4x + 2 имеет такой вид:
При изображении графика вершину нужно сместить в точку (-2;2). Третий способ позволяет узнать координаты вершины с помощью определения производной. Находить ее следует от заданной функции. Для вычисления координат вершины нужно действовать по следующему алгоритму:
Однако эти все три метода относятся к ручному вычислению. Автоматизация действий осуществляется с помощью специализированного программного обеспечения. Для этой цели подойдет онлайн-калькулятор, поддерживающий функцию нахождения точек вершины квадратичной кривой. Программы рекомендуется применять только для проверки решения, поскольку очень важно знать методы нахождения этой точки.
Алгоритм построения
В различных задачах нужно выполнить построение графика функции. В некоторых случаях даются координаты вершины, а в других — их следует искать, используя какой-либо метод. Чтобы построить квадратичную функцию, нужно воспользоваться таким алгоритмом:
Специалисты-математики настоятельно рекомендуют не усложнять вычисления. Возможно, в школьных программах и рассматриваются различные случаи. Однако в высших учебных заведениях основной аспект изучения дисциплин с физико-математическим уклоном сводится к оптимизации процесса решения задачи.
Примеры решений
В математике существует определенная классификация заданий на простые и сложные типы. Все они считаются однотипными, но отличаются только объемами вычислений и необходимостью построения графиков. Для решения нужно воспользоваться рекомендуемыми алгоритмами, которые существенно оптимизируют вычисления.
«Корень» трудностей при расчете — отсутствие систематизации вычислений. Не все ими пользуются. В результате простая задача становится очень сложной, поскольку в ней присутствует много ненужных вычислений. Кроме того, как отмечалось выше, рекомендуется «набить руку» на ручных вычислениях, ведь не всегда можно будет воспользоваться программами.
Упрощенная задача
Простым примером задания является следующий: необходимо вычислить координаты вершины точки параболы y = x 2 + 3x — 18. Следует продемонстрировать решение тремя способами. Решение первым методом:
Следовательно, вершина находится в точке (-1,5;20,25). Второй способ решения данной задачи имеет такой вид:
Повышенная сложность
Задания повышенной сложности сводятся к вычислению нескольких значений. Кроме того, в некоторых случаях следует построить график параболы y = x 2 — 7x +10. Необходимо выполнить такие действия:
Точек пересечения по ОУ нет. Они есть по оси абсцисс. Следует приравнять функцию к 0. Нахождение корней выполняется по теореме Виета: x1 = 2 и x2 = 5.
| y | 4 | 0 | -2 | -2,25 | -2 | 0 | 4 |
| x | 1 | 2 | 3 | 3,5 | 4 | 5 | 6 |
Таблица 1. Зависимость y от x.
После заполнения таблицы следует построить график искомой функции (рис. 3). Таблица состоит из следующих элементов: вершины, точек пересечения с осью абсцисс и 4 произвольных значений.
Рисунок 3. График функции.
Математики рекомендуют использовать для построения графика полученные значения при расчетах, поскольку подстановка и вычисление произвольных х существенно снижает скорость вычислений.
Таким образом, нахождение координат вершины параболы является довольно простой задачей, поскольку существует несколько методов. Из них можно выбрать оптимальный, который подходит в конкретной ситуации.