Как измеряют угол менее 60 градусов
§ 13. Инструменты для измерения углов
При слесарной обработке широко применяются угольники, угломеры, шаблоны угловые и угловые меры (плитки).
Угольники 90° (ГОСТ 3749—65) предназначены для проверки и разметки прямых углов, для контроля взаимно перпендикулярного расположения поверхностей деталей при монтаже различных видов оборудования и для проверки точности станков.
Угольники изготовляют из инструментальной легированной стали ХГ и X, углеродистой стали марок 10; 15; 20 и 50, а также из инструментальной углеродистой стали марки У8.
Промышленность выпускает угольники с углами 45; 60; 90 и 120° и специальные угольники с углами 30; 45; 90; 120 и 135° (рис. 67, а). Если требуются угольники с другими углами, то их изготовляют в виде шаблонов, например для проверки углов сверл, резьбы, шаблон типа «ласточкина хвоста» и др.
Рис. 67. Угольники:
а — специальный; б — лекальные; 1 — плоский, 2 — с широким основанием, 3 — с уровнем; в — приемы измерения угольником угла и плоскости
По ГОСТ 3749—65 угольники выпускаются четырех классов точности 0, 1,2, 3-й. Наиболее точные — угольники класса 0.
Точные угольники с фасками называются лекальными. Угольники 1-го класса точности применяют в инструментальном производстве для особо точных работ, 2-го класса — для выполнения слесарных работ повышенной точности, 3-го класса — для грубых работ.
Применяют следующие типы лекальных угольников (рис. 67, б): плоский 1, с широким основанием 2, с уровнем 3.
У лекальных угольников края длинной стороны скошены с обеих сторон. Скосы дают возможность точнее обработать угольник. Таким угольником удобно определять отклонения в углах проверяемого изделия методом световой щели (на просвет).
Угольники с широким основанием (аншлажные) предназначены для проверки прямого угла у изделия при установке его на проверочной плите.
При проверке внутренних углов угольник прикладывают к поверхности детали наружной частью (рис. 67, в), а при проверке наружного угла — внутренней частью. По просвету между угольником и проверяемой деталью на глаз (а иногда щупом) определяют отклонение угла.
Угломеры с нониусом (ГОСТ 5378—66) применяют для измерения углов контактным методом с отсчетом по угловому нониусу. В настоящее время широко распространены угломеры типа I (УН) и величиной отсчета по нониусу 2′ (2 мин) и 5′ (5 мин).
Угломер типа I (рис. 68, а), предназначенный для измерения наружных углов от О до 180° и внутренних углов от 40 до 180°, состоит из полукруглого основания (диска) 5, скрепленного со съемной линейкой 4. Подвижная линейка 10 вращается на оси 2 вместе с сектором 3, на котором закреплен нониус 8. Микрометрическая подача б подвижной линейки 10 осуществляется гайкой 7, после чего линейка 10 закрепляется стопором 9.
Рис. 68. Угломер типа I (а) и прием измерения угломером (б)
Измерение углов от 0 до 90° производится с помощью угольника 1, углы более 90° измеряются без угольника 1. На шкале нониуса нанесено 30 делений; каждое деление соответствует 2 минутам.
Угломер накладывают на проверяемую деталь так, чтобы линейки 10 и 4 были совмещены со сторонами измеряемого утла. Целое число градусов отсчитывают по шкале диска до нулевого штриха нониуса. Затем определяют штрих нониуса, совпадающий со штрихом основной шкалы. После следует определить на нониусе число минут, обозначенное ближайшим меньшим числом, совпадающим со штрихом нониуса. Показания градусов и минут складываются, причем минуты нужно умножить на точность отсчета.
Прием измерения угломером показан на рис. 68, б.
Угломер типа II (УМ) предназначается для измерения наружных углов от 0 до 180° (рис. 69) с величиной отсчета по нониусу 15′ (15 мин).
Рис. 69. Угломер типа II
Угломер состоит из полукруглого основания 1, на котором закреплена линейка 2. Сектор 3 с нониусом 8 перемещается по основанию 1 и после установки закрепляется винтом 4. К сектору 3 при помощи державки 7 крепится угольник 5, а к нему присоединяется съемная линейка 6. Этим угломером можно измерить не только наружные, но и внутренние углы.
Проверку погрешности показаний угломеров следует производить по угловым плиткам в пяти — семи точках, равномерно расположенных по основной шкале нониуса.
Более точно углы проверяются при помощи угловых призматических плиток (ГОСТ 2875—62), которые подбираются в блоки (рис. 70).
Рис. 70. Набор угловых плиток (а), прием проверки угла (б)
Как измеряют угол менее 60 градусов
§ 100. Инструменты для измерения углов
Для измерения наружных и внутренних углов в слесарном деле применяют угольники, угломеры и угломерные плитки.
Угольники с широким основанием (аншлажные) отличаются тем, что короткое их основание толще длинной полки. Таким угольником удобно определять отклонения в углах проверяемого изделия способом световой щели (на просвет) при установке изделия на поверочной плите.
Угольники цилиндрические применяют для этой же цели!
Угломеры предназначаются для измерения углов. Изготовляют следующих типов:
Угломер типа УМ (рис. 396,а) с величиной отсчета по шкале нониуса 2′ (2 угловых минуты) предназначен для измерения наружных углов от 0 до 180°. Угломер имеет полукруглое основание (полудиск) 5 со шкалой угловых градусов, соединенное со съемной линейкой 4 и подвижной линейкой 10, вращающейся на оси 2 вместе с сектором 3. Точность установки подвижной линейки 10 осуществляется при помощи микрометрической подачи 6 вращением гайки 7 и фиксированием стопором 9.
Перед применением угломер протирают и проверяют нулевое положение: нулевые
штрихи основания и нониуса должны совпадать.
При совпадении штрихов нониуса и основания между измерительными поверхностями угломера не должно быть просвета. Это проверяется соединением измерительных поверхностей (рис. 396,в) или при помощи лекального угольника (рис. 396,г).
При измерении угломер накладывают на проверяемую деталь так, чтобы линейки 4 и 10 были совмещены со сторонами измеряемого угла. Прижимая слегка правой рукой деталь к измерительной поверхности линейки основания, перемещают деталь постепенно, уменьшая просвет до полного соприкосновения. После этого (если нет просвета)фиксируют положение стопором и читают показание. Целое число градусов отсчитывают по шкале основания слева направо нулевым штрихом нониуса.
После этого находят штрих нониуса, совпадающий со штрихом шкалы основания, и ближайшую к нему слева цифру нониуса. К этой цифре прибавляют результат умножения величины отсчета на порядковый номер совпадающего штриха нониуса, считая его от найденной цифры нониуса. При чтении угломер держат прямо перед глазами. Например, нулевой штрих нониуса прошел 34-е деление шкалы основания, но не дошел до 35-го, при этом со штрихом основной шкалы совпадает 20-й (не считая нулевого) штрих шкалы нониуса. Следовательно, измеряемый угол составляет 34 + 20х 2 = 34°40′.
Для измерения углов от 0 до 90° угломер соединяют с угольником (рис. 397,а), а для измерения углов от 90 до 180° угломер применяют без угольника (рис. 397,6) и к его показаниям прибавляют 90°.
Угломер типа УН с величиной отсчета по нониусу 2 или 5′(угловых минут, рис. 398,в,6) конструкции Семенова, выпускаемый заводом «Калибр», является наиболее удобным для измерения наружных углов от 0 до 180° и внутренних углов от 40 до 180°. Угломер имеет полукруглое основание 6, на котором закреплена линейка В основания. Сектор 7 с нониусом 3 перемещается по основанию 6 и после установки закрепляется стопором 5. Микрометрическая подача нониуса осуществляется вращением микрометрического винта 4. К сектору 7 при помощи державок 2 крепится угольник 7, а к нему присоединяется съемная линейка 9.
Если на угломере установлены угольник и линейка (рис. 399,а), то можно измерять углы от 0 до 50°. Если убрать угольник и на его месте закрепить линейку, можно измерять углы от 50 до 140° (рис. 399,6), если убрать линейку и оставить только угольник (рис. 399,в), можно измерять углы от 140 до 230°. При отсутствии линейки и угольника (рис. 399,г) можно измерять углы от 230 до 320°.
Точность отсчета, полученного при измерении угловых величин или при установке заданного угла, проверяют по градусной шкале и нониусу. По шкале градусов, размещенной на дуге основания, определяют, на каком целом делении (или между ними) остановилось нулевое деление нониуса, которое соответствует числу целых градусов угловой величины. По шкале нониуса определяют, какое из его делений совпало с делением шкалы градусов, по цифрам нониуса определяют число минут.
Угол. Измерение углов.
Измерение углов сводится к измерению соответствующих им дуг следующим образом. За единицу углов принимают угол, составляющий 1/90 часть прямого угла. Эту единицу называют угловым градусом.
За единицу дуг одинакового радиуса принимают такую дугу того же радиуса, которая соответствует центральному углу, равному угловому градусу. Такая дуга называется дуговым градусом.
Так как прямому центральному углу соответствует 1/4 окружности, то угловому градусу соответствует 1/90 четверти окружности. Значит, дуговой градус составляет 1/360 целой окружности.
Пусть требуется измерить угол AOB, то есть найти отношение этого угла к угловому градусу MNP.Для этого опишем из вершин углов дуги СD и EF произвольным, но одинаковым радиусом.
Следовательно, эту пропорцию можно выразить так: число, измеряющее угол в угловых градусах, равно числу, измеряющему соответствующую дугу в дуговых градусах.
Для краткости эту фразу выражают обыкновенно так: Угол измеряется соответствующей ему дугой.
Градусы угла или дуги подразделяются на 60 равных частей, называемых минутами (угловыми или дуговыми).
Минуту разделяют на 60 равных частей, называемых секундами (угловыми или дуговыми).
Из сказанного выше следует, что в угле содержится столько угловых градусов, минут и секунд, сколько в соответствующей ему дуге заключается дуговых градусов, минут и секунд.
Если, например, в дуге СD содержится 40 град. 25 мин. и 13,5 секунды (дуговых), то и в угле AOB заключается 40 град. 25 мин. 13,5 сек. (угловых). Это выражают сокращенно так:
обозначая значками (°), (‘), (‘’) соответственно градусы, минуты и секунды.
Так как прямой угол содержит 90°, то :
1. сумма углов всякого треугольника равна 180 °;
2. сумма острых углов прямоугольного треугольника равна 90°;
3. каждый угол равностороннего треугольника равен 60°;
Чтобы измерить угол AOB, накладывают на него прибор так, чтобы центр полукруга совпал с вершиной угла, а радиусом OM совпал со стороной AO. Тогда число градусов, содержащееся в дуге PN, покажет величину угла AOB. При помощи транспортира можно также начертить угол, содержащий данное число градусов.
Конечно, на таком приборе нет возможности отсчитывать не только секунды, но и минуты. Измерение и построение можно выполнить только приближенно.
Углы 30, 45, 60, 90 градусов: наглядные, стихотворные, боевые, электрические, драматические, музыкальные
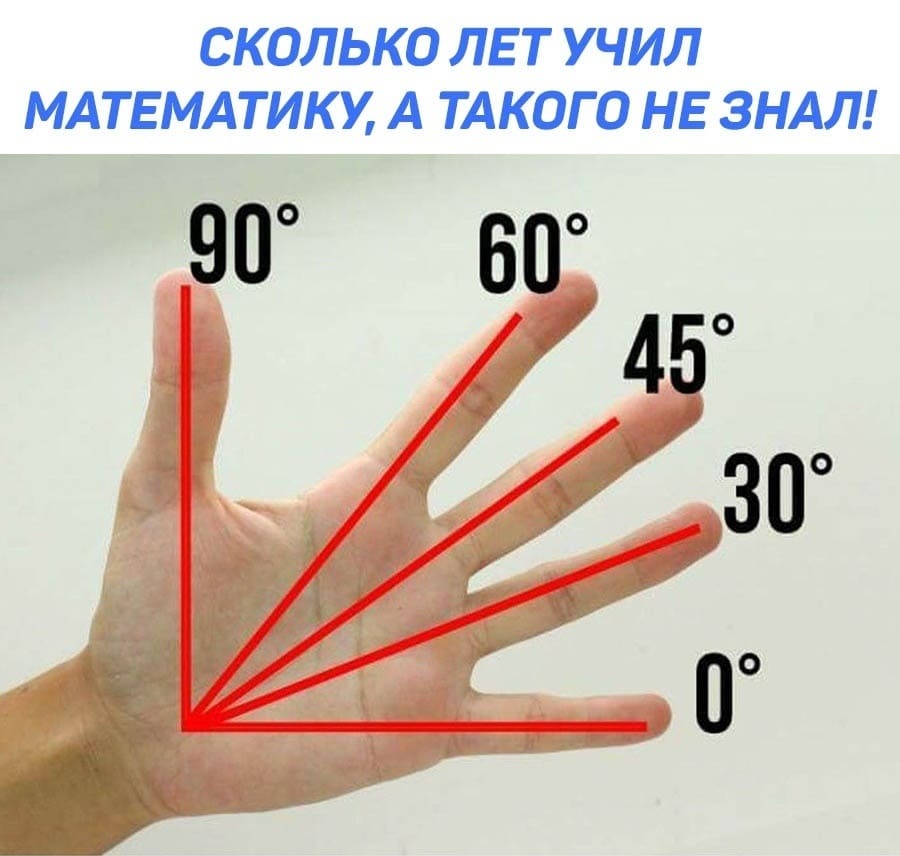
Можно определить углы 30, 45, 60, 90 градусов с помощью своей ладони.
Градусы наглядные: как их определить с помощью своей ладони
Наша рука, оказывается, очень даже может помочь с величинами углов, с градусами. Если посмотреть на нее под определенным углом зрения (см. рис. 1), то вот они, родимые: 0 градусов, 30, 45, 60 и даже 90 градусов!
Почему нам так важны именно эти величины? Почему нас могут интересовать углы 0, 30, 60 и 90 градусов, а также 45? Нет бы поинтересоваться, скажем, углами 15, 20, 75 или 80 градусов…
Оказывается, все дело в синусах и косинусах! Ибо синус нуля градусов есть ноль, а косинус 90 градусов — тоже равен нулю. Синус 30 градусов равен половинке единицы. Такое же значение 0,5 дает косинус 60 градусов.
А вот 45 градусов интересны тем, что синус и косинус 45 градусов равны между собой. Это значит, что тангенс 45 градусов будет равен единице. Ведь мы помним, что тангенс угла есть частное от деления синуса угла на косинус угла.
Но не только об этом хотелось сказать, глядя на рисунок…
Градусы стихотворные и число «пи»
Есть такое число – «пи». Оно почему-то равно 3,14. Хотя не совсем так. Это число с бесконечным количеством цифр после запятой. После запятой стоят не только цифры 1 и 4, но и множество других цифр.
Первый десяток цифр числа «пи» легко написать, если запомнить необычное стихотворение. Правда, стихи про «пи» нужно писать со старинной буквой «ять» — ведь и число «пи» очень старое, и стихотворение совсем не молодое:
Кто и шутя, и скоро пожелаетъ
Пи узнать число — ужъ знаетъ
Зачем в стихотворении стоит «ять» на конце? И при чем тут «пи»? Все очень просто: считаем буквы в словах стихотворения и подставляем цифры в число «пи».
Получается, кто=3, и=1, шутя=4, и=1, скоро=5 и так далее: 3,1415926536… Многоточие на конце — это значит, что есть продолжение цифрам, бесконечное продолжение.
Причем тут градусы? При том, что «пи» — это величина развернутого угла, но не в градусах, а в радианах (другая единица измерения величины угла). «Пи» радиан есть угол величиной 180 градусов.
Как говорят математики, отсюда нетрудно догадаться, что 0 градусов есть ноль радиан. 90 градусов есть «пи пополам» радиан. Нам этот термин «пи пополам» еще пригодится далее. Все остальные градусы таким же образом можно свести к разным частям числа «пи».
Получается, что мы теперь знаем стишок про 180 градусов — стишок про «пи»! Что это дает?
Градусы боевые: почему наши деды победили
Штурман откладывает карту в сторону. Достает маневренный планшет. Теперь он отслеживает на нем положение корабля относительно одного противника или сразу нескольких противников.
Тут — сплошные градусы. Кто из супостатов виден под каким углом? Угол есть решающая величина. Приходится учитывать как углы, так и их синусы, и косинусы.
Кто в школе учился, тот помнит, что синус и косинус угла не может быть больше единицы. Хоть что делай, больше единицы не получается.
А вот в годы войны у штурмана боевого корабля косинусы углов доходили порой до четырех! Потому и победили, что делали невозможное! Даже с косинусами, ограниченными правильной математикой!
Так что запомним вопреки математике: в годы войны косинусы углов могут доходить до «четырех». В том числе, поэтому наши деды победили!
Градусы электрические: отклонение между напряжением и током
Ну, синус? Ну, косинус? И что тут такого? Спросим любого человека, например, возле пивного ларька, что такое синус и как давно он пользовался косинусом после школы. Что услышим в ответ?! Во, именно «это» и услышим.
Вместе с тем мы постоянно живем, можно сказать, под градусом, точнее, под косинусом! Ежедневно мы пользуемся электричеством: нажимаем кнопки и выключатели, и дело с концом — все светится, крутится, работает.
Чтобы электричество выполняло свое предназначение, нужно электрическое напряжение и электрический ток. Обе «субстанции» должны быть вместе и одновременно. Но эти две величины могут иметь между собой угол отклонения, измеряемый «косинусом фи», как выражаются энергетики на своем профессиональном языке.
Если отклонение напряжения от тока есть ноль градусов, то электрическая мощность будет получена умножением величины напряжения на величину тока.
Допустим, подключаем электрообогреватель. Он начинает излучать тепло, равное по мощности этой самой величине: напряжение 220В (двести двадцать вольт) умножить на ток, скажем, 5А (пять ампер) равно 1КВт (1 киловатт) мощности. Становится тепло!
Если между напряжением и током есть отклонение, хотя бы на 1 градус, то придется перемножать не только напряжение и ток, но и полученный результат дополнительно умножать на косинус угла отклонения. Ноль градусов отклонения — косинус равен единице, умножение на единицу ничего не меняет. А вот косинус всего лишь 1-го градуса возможного отклонения уже меньше единицы. Не намного, но меньше. Это значит, что греть наша батарея будет уже слабее.
Чем больше отклонение электрического напряжения от электрического тока, чем будет больше между ними градусов так называемого угла «фи». Тем слабее будут греть батареи, хуже станет накал лампочек, и вообще будет меньше электричества.
И не говорите теперь, что косинус — это абстракция, которую мы оставили в школе навсегда…
Градусы драматические: косинус 90 градусов равен нулю
А что как напряжение и ток отклоняются друг от друга на 90 градусов?! Ведь косинус такого угла равен нулю. Умножение на ноль есть ноль. Это, что называется, страшный сон энергетиков — ужасная апокалиптическая драма!
Представьте себе, газ сжигается на тепловых электростанциях, вода крутит турбины на гидроэлектростанциях, нейтроны делятся в реакторах атомных электростанций. Ток «бежит» по проводам в дома. А там — косинус угла «фи» равен нулю — полный швах! Батареи не греют, лампочки не светятся, холодильники не работают.
Чтобы мысленный эксперимент с отклонением напряжения и тока на 90 градусов не стал реальностью, энергетики по всему миру постоянно следят за «косинусом фи». Денно и нощно, без устали, без перерывов.
Почему отклоняются напряжение и ток? Из-за потребителей электричества! Нет, не из-за домашних электрических обогревателей. И не из-за домашних лампочек накаливания. Но из-за оборудования заводов и фабрик.
Везде, где крутятся электромоторы, их «кручение» приводит как бы к обратному закручиванию электричества. Работающее оборудование возвращает энергетикам в электрические сети сдвинутое между собой напряжение и ток.
Образно говоря, чтобы крутить моторы, электричество должно «упираться» во что-то. И из-за этого понемногу «проворачивается» в обратную сторону. Что и приводит к возникновению угла сдвига между напряжением и током.
Если не следить за последствиями такого «сдвига», то угол между напряжением и током будет постоянно расти. Косинус фи начнет уменьшаться. Электростанции начнут работать сначала чуть-чуть вхолостую, потом все больше и больше, потом еще больше…
Градусы из радиоточки
Если напряжение и ток встанут друг относительно друга на 90 градусов — это будет недопустимое отклонение или «сдвиг по фазе на пи пополам»! Тогда электричество останется в проводах, но оно ничего не будет греть, освещать, двигать.
«Сдвиг по фазе на пи пополам» есть расхожее выражение, которое означает абсолютную неприемлемость того или иного действия, поступка.
Пришло оно к нам из того самого электротехнического «косинуса фи».
Про сдвиг между напряжением и током можно написать не одну драму с яркими событиями и участниками. Но мы не будем это делать, ибо наши энергетики не допустят подобного хода событий…
Кстати, кто помнит еще советское радио, что звучало практически в каждом доме? Там по утрам во многих городах сообщали не только про погоду. Погода — это тоже градусы, но другие.
Из радиоточки строго так говорили, обычно после прогноза погоды: «на сегодня режим энергопотребления установлен два тире два» или «. два тире один». Это про «наши» градусы, про «косинус фи»!
Что это за режимы такие: 2-2, 2-1 и другое? То были прямые указания предприятиям, как они должны именно сегодня компенсировать возникающие сдвиги между напряжением и током.
Энергетики шли к компенсирующим установкам и включали озвученные по радио режимы. Вот ведь насколько важны углы! Про них даже по центральному радио (с местным уклоном, разумеется) вещали ежедневно.
А вы говорите градусы, синусы, косинусы! И зачем мы их в школе «проходили», если вокруг нас их как не было, так и нет? Оказывается, были, есть и будут. Даже в обычной электрической розетке, в лампочке, в утюге.
Градусы музыкальные
Для тех, кто «добрался» до конца — маленький сюрприз: музыкальные «градусы». Вот как, оказывается, можно сыграть на фортепиано про число «пи» с точностью аж до 122 знаков после запятой. Музыка «развернутого угла 180 градусов»!
Словами добавить нечего, достаточно послушать. И все это про «пи» и про градусы, которые в школе «прошли» и забыли:
Геометрия. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Градус – угол, равный одной сто восьмидесятой части развернутого угла.
Градусная мера угла – положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Минута – 1/60 часть градуса.
Секунда – 1/60 часть минуты.
Луч – часть прямой, состоящий из всех точек, лежащих по одну сторону от заданной точки, которая является началом луча.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Стороны угла – лучи, из которых состоит угол.
Вершина угла – общее начало сторон угла.
Биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.
Теоретический материал для самостоятельного изучения.
Ранее вы уже познакомились с геометрической фигурой – уголи его составными элементами.
Сегодня мы продолжим изучать углы, познакомимся с их классификацией и будем измерять углы с помощью транспортира.
Измерение углов аналогично измерению отрезков – оно основано на сравнении, только отрезки сравнивались с отрезком, принятым за единицу измерения, а углы с углом, тоже принятым за единицу измерения.
Обычно за единицу измерения углов принимают градус.
Градус – угол, равный 1/180 части развёрнутого угла.
Положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу, называется градусной мерой угла.
Для измерения углов используют транспортир. Вспомним, как проводить измерение углов с помощью транспортира.
Транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах на той же шкале.
Но обычно говорят кратко – угол О равен 50 градусам.
Если масштабныйугол не укладываетсяцелое число раз в измеряемом угле, тоединицу измерения делят ещё на части.
Определённые части градуса носят специальные названия.
Минута – 1/60 часть градуса.
Секунда – 1/60 часть минуты.
Далее, аналогично понятию равные отрезки, ведём понятие равные углы.
Дваугла считаются равными, если градус и его части укладываются в этих углах одинаковое число раз, т.е. равные углы имеют равные градусные меры.
Если один угол меньше другого, то градус в нём (или его часть) укладываются в этом углу меньшее число раз, чем в другом, т.е. меньший угол имеет меньшую градусную меру.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
Далее рассмотрим классификацию углов.
Мы уже знаем, что есть развёрнутый угол, его градусная мера сто восемьдесят градусов.
Но есть и другие углы.
Например, прямой угол, его градусная мера девяносто градусов;
острый угол, его градусная мера меньше девяноста градусов;
тупой угол, его градусная мера больше девяноста градусов, но меньше ста восьмидесяти.
Выполним практическое задание – построим биссектрису угла с помощью транспортира.
Мы знаем, что биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.
OL – биссектриса ∠АОС.
Поэтому для начала определим градусную меру ∠АОС, она составляет 128°, тогда биссектриса этого угла, исходя из определения, составит 64 °.
Итак, сегодня получили представление о том, как измерять и изображать угол с помощью транспортира. Перейдем к практическим заданиям.
Способы измерения на местности.
Измерение углов на местности проводят с помощью различных приборов. Один из таких – астролябия, она состоит из диска (лимб), разбитого на градусы и вращающейся вокруг центра диска линейки (алидады). На концах алидады есть окошечки, которые нужны, чтобы устанавливать её в определённом направлении.
Опишем, как происходит измерение углов с помощью этого прибора. При измерении углов астролябию устанавливают в его вершине, например, точке О, при этом лимб должен находится горизонтально плоскости угла, а отвес, в центе диска, совпадать с вершиной угла.
Затем устанавливаем алидаду вдоль одной из сторон угла, например, АО, отмечаем деление, напротив которого находится указатель алидады.
Далее поворачиваем алидаду по часовой стрелке, пока она не совпадёт со второй стороной угла, у нас это сторона ОВ, отмечаем деление, напротив которого оказался указатель алидады. Теперь можно найти градусную меру измеряемого угла, как разность второго и первого измерения.
1. Луч ВК делит развернутый ∠ОВС на два угла, разность которых равна 56°. Найдите образовавшиеся углы.
Решение: нарисуем рисунок, исходя из условия задачи.
Обозначим ∠СВК за х, тогда ∠ОВК= х + 56°, исходя из условия задачи (разность углов равна 56°). Развёрнутый угол равен 180°. Составим уравнение и решим его.
Тогда ∠ОВК= х + 56°= 62° +56° = 118°.
Ответ: ∠СВК = 62°; ∠ОВК = 118°.
2. Чему равен ∠ЕОА, если ∠ВОА = 130° 54´, а ∠ВОЕ = 105° 76´?
Решение: Найдём ∠ЕОА = ∠ВОА – ∠ВОЕ, т.к. ОЕ – луч, проведённый из вершины ∠ВОА и делящий этот угол на 2 части. Подставим в выражение градусные меры углов и найдём градусную меру ∠ЕОА. Так как в градусе 60 минут, то 105° 76´ = 106° 16´.