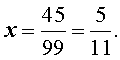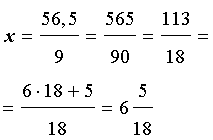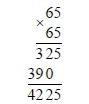Как называется бесконечная десятичная дробь
Бесконечные периодические и непериодические десятичные дроби
Содержание
Бесконечные периодические и непериодические десятичные дроби
В десятичной записи конечной десятичной дроби после запятой стоит конечное число десятичных знаков.
В десятичной записи бесконечной десятичной дроби после запятой стоит бесконечное число десятичных знаков.
Бесконечные десятичные дроби бывают периодическими и непериодическими.
Повторяющаяся группа цифр называется периодом бесконечной периодической десятичной дроби.
Для обозначения периода десятичной дроби используют круглые скобки.
Бесконечная десятичная дробь, не являющаяся периодической, называется непериодической.
Алгоритм обращения бесконечной периодической десятичной дроби в простую дробь
Разберем алгоритм обращения бесконечной периодической десятичной дроби в простую дробь на примере решений следующих задач.
ОТВЕТ : 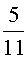
ОТВЕТ : 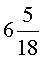
Демонстрационные варианты ЕГЭ и ОГЭ
С демонстрационными вариантами ЕГЭ и ОГЭ по всем предметам, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.
Наши учебные пособия для школьников
При подготовке к ЕГЭ и к ОГЭ по математике Вам могут также пригодиться наши учебные пособия.
Бесконечные периодические десятичные дроби
В данной публикации мы рассмотрим, что из себя представляют бесконечные периодические десятичные дроби, какие бывают виды, и как их можно перевести в обыкновенную дробь. Также разберем примеры для закрепления материала.
Периодические десятичные дроби
Определение
Если в дробной части бесконечной десятичной дроби есть один или несколько цифр, которые повторяются в одной и той же последовательности, такая дробь является периодической.
Примеры периодических десятичных дробей:
Запись
Повторяющаяся цифра/цифры – это период дроби, который пишется в скобке для сокращения длины записи. Например, дроби выше сокращенно следует писать так:
Произношение
Чистые периодические дроби – это такие бесконечные десятичные дроби, период которых начинается сразу после запятой.
Смешанные периодические дроби – бесконечные десятичные дроби, у которых между запятой и периодом присутствует одна и более цифр (их количество ограничено).
Перевод периодической десятичной дроби в обыкновенную
Для того, чтобы перевести периодическую дробь в обыкновенную (простую), выполняем следующие шаги:
Пример 1
Давайте переведем число 0,8(3) в обыкновенную дробь.
Действовать будет пошагово согласно инструкции выше:
1. n = 1
2. m = 1
3. a = 83
4. b = 8
5. x = 0
6. Остается только применить формулу:
Пример 2
Представим периодическую дробь 2,64(378) в виде обыкновенной.
1. n = 3
2. m = 2
3. a = 64378
4. b = 64
5. x = 2
6. Подставляем эти значения в формулу нахождения простой дроби и получаем:
Бесконечные дроби и иррациональные числа
теория по математике 📈 числа и вычисления
При переводе обыкновенной дроби в десятичную можно получить конечную периодическую или бесконечную десятичные дроби (кроме простой десятичной, разумеется).
Конечная десятичная дробь
Конечная десятичная дробь – десятичная дробь с конечным числом знаков после запятой, то есть когда у аналога обыкновенной дроби числитель без остатка делится на знаменатель.
Пример №1. ¾ — делим 3 на 4 и получаем 0,75.
Пример №2. 31 /50 делим 31 на 50 и получаем 0,62.
Пример №3. 3 /25 делим 3 на 25 и получаем 0,12.
Периодическая десятичная дробь
Периодическая десятичная дробь – дробь, у которой после запятой (в дробной части) присутствует бесконечный повтор одной цифры или сочетания нескольких одинаковых цифр.
Пример №4. 7 /12 При делении 7 на 12 получается 0,5833333…, где постоянно повторяется цифра 3, запись делают следующим образом: 0,58(3); читается эта дробь следующим образом: нуль целых пятьдесят восемь сотых и три в периоде.
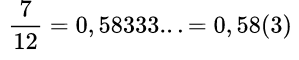
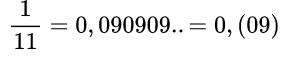
Иррациональные числа — числа, которые не могут быть представлены в виде обыкновенной дроби.
Значение какого из выражений является рациональным числом?
В данном задании у нас проверяют навыки операций с иррациональными числами.
Разберем каждый вариант ответа в решении:
√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…
При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.
При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:
Но √15 является иррациональным, поэтому данный вариант ответа не подходит.
При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:
Данный вариант ответа нам подходит.
Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.
pазбирался: Даниил Романович | обсудить разбор | оценить
Какое из данных чисел является рациональным?
Для решения этой задачи нужно действовать следующим образом:
Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:
Рассмотри каждое из них:
Следовательно, число √0,81 является рациональным, остальные же числа
хотя и похожи на форму 9 в квадрате, не являются рациональными.
Таким образом, правильный ответ третий.
pазбирался: Даниил Романович | обсудить разбор | оценить
Значение какого из данных ниже выражений является наибольшим?
Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:
Переносим 3 под корень:
Переносим 2 под корень:
2√11 = √(2² • 11) = √(4 • 11) =√44
Переносим 2 под корень:
2√10 = √(2² • 10) = √(4 • 10) =√40
Возводим 6,5 в квадрат:
Посмотрим на все получившиеся варианты:
Следовательно, правильный ответ первый.
pазбирался: Даниил Романович | обсудить разбор | оценить
Для решения этого задания достаточно представлять себе значения чисел меньше и больше заданного, корни которых подлежат вычислению.
Значит, нам подходит третий вариант ответа — √38.
pазбирался: Даниил Романович | обсудить разбор | оценить
Десятичные дроби — для чайников
Действия с десятичными дробями – деление умножение, сложение, вычитание, сравнение. Разбор примеров.
Между прочим, большинство ошибок на экзаменах происходят как раз из-за незнания простейших действий вроде этих.
Так что читай эту статью и отрабатывай скиллы.
Десятичные дроби — коротко о главном
1. Определение
Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени.
2. Конечная и бесконечная десятичная дробь
Десятичная дробь может быть:
3. Свойства десятичных дробей
4. Сложение десятичных дробей
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.
5. Вычитание десятичных дробей
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:
6. Умножение десятичных дробей
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
7. Деление десятичных дробей
Деление десятичной дроби на натуральное число
Деление десятичных дробей друг на друга
Десятичные дроби — подробнее
Конечно, ты знаешь, что такое обыкновенная дробь. Например, \( \displaystyle \frac<1><3>,\ \frac<1><4>,\frac<5><112>\).
Наравне с приведенными выше дробями существуют дроби \( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\) и т.д.
Такие дроби можно записать намного удобнее и более кратко, то есть:
Данного вида дроби называются десятичными. Иными словами:
Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени (первый пример – \( 10\) в первой степени, второй – \( 10\) во второй степени и т.д.).
Ты наверняка знаешь, что каждая цифра после запятой имеет свое название. На всякий случай напомню тебе про них, чтобы в дальнейшем мы говорили на одном языке:
Это огромное число читается по следующему алгоритму:
А теперь прочитаем все вместе – «\( 46\) целых одна тысяча двести тридцать четыре десятитысячные». Разобрался? Переходим к визуализации полученных знаний!
Итак, небольшая тренировка на понимание, что такое эта десятичная дробь! Нарисуй квадрат \( 10\) на \( 10\) и закрась какую-нибудь его часть равную:
Справился? Проверяем, что у тебя получилось.
Во-первых, квадрат \( 10\) на \( 10\) состоит из \( 100\) клеточек. Соответственно, \( 0.05\) – \( 5\) клеточек из \( 100\); \( 0,4\) – \( 40\) клеточек из \( 100\) и так далее.
С понятиями разобрались, теперь научимся переводить из десятичной дроби в обыкновенную и обратно.
Перевод из десятичной дроби в обыкновенную и обратно
Уверена, что ты с легкостью справился! А как насчет обратного перевода? Из обыкновенных в десятичные?
Попробуй свои силы на вот этих дробях:
Если ты со всем справился, можешь пропускать следующий абзац, а если где-то допустил ошибку, внимательно прочти о том, как легко и 100% правильно переводить дроби из обыкновенных в десятичные.
Разобрался? Посмотри еще раз эту маленькую «инструкцию»:
Я думаю, ты во всем-всем разобрался! Потренируемся? Попробуй поработать еще с вот этими дробями:
Виды десятичных дробей
Десятичная дробь может быть:
Поговорим сначала о конечных дробях.
Конечная десятичная дробь
Само собой понятно, что дроби \( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\) являются конечными, ведь знаменатель дроби уже представлен как единица с последующими нулями, и поэтому мы сразу можем сказать, что данную обыкновенную дробь можно перевести в конечную десятичную. А что ты скажешь насчет этой дроби: \( \displaystyle \frac<1><4>\)? Ее знаменатель далеко не единица с последующими нулями, но ты четко знаешь, что у нее есть десятичный «аналог»:
То есть, чтобы определить, можно ли перевести дробь в десятичную, необходимо умножить числитель и знаменатель на одно и то же число, такое, чтобы знаменатель стал равен \( 10\), \( 100\), \( 1000\) и так далее.
Усвоил? Постарайся представить в виде конечной десятичной дроби следующие обыкновенные дроби:
Сравним наши ответы:
Справился? Молодец. Выходим на новый уровень и переходим к бесконечным десятичным дробям.
Бесконечная десятичная дробь
Итак, бери калькулятор и дели \( 1\) на \( 17\). Поделил? Ты получил \( 0,05882352941\) и дальше окошко калькулятора не показывает… Это тоже является десятичной дробью, только данная десятичная дробь является бесконечной. Ты сейчас скажешь, а как же наше определение?
Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени (первый пример – \( 10\) в первой степени, второй – \( 10\) во второй степени и т.д.).
Все очень просто и никаких противоречий с определением нет. В данном случае нам необходимо привести наш знаменатель к \( <<10>^
Бесконечной десятичной дробью называется обыкновенная дробь, в записи которой после запятой содержится бесконечное количество цифр.
Как правило, в задачах, где встречаются бесконечные десятичные дроби, просят указать ответ либо с округлением (например, до десятых, или до сотых), либо записать в виде обыкновенной дроби, то есть как \( \displaystyle \frac<1><17>\).
Подумай, какой самый популярный пример можно привести на тему «бесконечная десятичная дробь»? Правильно! Число \( \pi \) является бесконечной десятичной дробью. Во всем мире люди договорились, что для решения математических задач принято, что \( \pi =3,14\), но это далеко не так. Число \( \pi \) не имеет определенного завершения. Оно настолько бесконечно, что ежегодно в мире проводятся соревнования по запоминанию числа \( \pi \). Мировой рекорд по запоминанию знаков числа \( \pi \) после запятой принадлежит китайцу Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67 890 знаков после запятой без ошибки! Все 67 890 знаков после запятой мы приводить не будем, а приведем несколько сокращенную запись:
Думаю, этого хватит, чтобы оценить «масштабы» данного числа.
Наравне с бесконечными десятичными дробями существуют периодические десятичные дроби. Они так же не имеют конца, но последующие числа в них повторяются, например, попробуй перевести в десятичную дробь \( \displaystyle \frac<1><3>\). Что у тебя получилось?
Чтобы не повторять число \( 3\) много много раз, решили говорить «ноль целых и три в периоде», так как тройка будет повторяться после запятой бесконечное число раз. Из этого умозаключения следует определение:
Дробь называется периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр.
Чтобы кратко записать такую дробь, период (повторяющиеся цифры после запятой) пишут в скобках:
\( \displaystyle \frac<1><3>=0,\underbrace<3>_<период>33333333….=0,\left( 3 \right)\)
\( \displaystyle \frac<1><7>=0,\underbrace<142857>_<<период>>\underbrace<142857>_<период>142…=0,\left( 142857 \right)\)
Важно, что период не может начинаться слева от запятой:
\( \displaystyle \frac<100><7>=\underbrace<14,2857>_<не период>1428571428571…=14,\left( 285714 \right)\).
Математика. 6 класс
Конспект урока
Бесконечные периодические десятичные дроби
Перечень рассматриваемых вопросов:
– понятие бесконечной периодической десятичной дроби;
– преобразование обыкновенных дробей в бесконечные периодические дроби;
– действия с периодическими дробями.
Бесконечная периодическая десятичная дробь – это дробь, у которой одна цифра или группа цифр повторяются. Повторяющаяся группа цифр называется периодом и записывается в скобках.
Любое рациональное число p/q можно разложить в периодическую десятичную дробь.
Любая периодическая дробь есть десятичное разложение некоторого рационального числа.
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Обыкновенную дробь можно разложить в конечную десятичную, если в знаменателе нет простых множителей, кроме 2 и 5.
Вы уже знаете, как это сделать.
1. Умножить числитель и знаменатель на одно и то же число, чтобы привести к знаменателю 10, 100, 1000 и т. д.;
2. Выполнить деление числителя на знаменатель.
Пример 1. Умножили числитель и знаменатель на 2.
Пример 2. Сначала сократили дробь.
Пример 3. Выполнили деление 3 на 125.
Рассмотрим примеры, когда привести к знаменателю 10, 100 и т. д. нельзя. Возможно только деление числителя на знаменатель.
Заметим, что при делении получаются повторяющиеся остатки и, соответственно, повторяющиеся цифры в частном. Из-за этого процесс деления бесконечен. Отсюда происходит бесконечная десятичная дробь.
Рассмотрим другие примеры.
Повторяющиеся цифры 3; 27; 6 называют периодом дроби. Бесконечные десятичные дроби 0,333…; 0,2727…; 0,1666… называют периодическими.
«Нуль целых и три в периоде»
«Нуль целых и 27 в периоде»
«Нуль целых одна десятая и шесть в периоде»
Периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или несколько цифр (период дроби).
Отметим, что любое рациональное число p/q разлагается в периодическую десятичную дробь.
Любая периодическая дробь есть десятичное разложение некоторого рационального числа.
Замечание. При делении уголком десятичное разложение с периодом 9 не возникает.
Далее рассмотрим, как выполняются действия с периодическими дробями?
Запишем дробь 1/3 в виде бесконечной периодической дроби 0,333…
Запишем дробь 0,3 в следующем виде 0,300… Приписывая бесконечно много нулей, мы превращаем конечную дробь в равную ей бесконечную периодическую дробь с периодом 0.
Теперь можем сравнить: 0,333… > 0,300…
2. Разложите обыкновенную дробь в бесконечную периодическую десятичную дробь, округлите до десятых.
Разбор заданий тренировочного модуля
Представьте в виде периодической дроби. В ответе укажите её период.
Используя предыдущие задания, запишите периодическую дробь в виде обыкновенной дроби: 0,(3); 0,(5); 0,(6).
Задание 3 ⃰ (повышенного уровня сложности)
Задача: периодическую дробь 0,(1) записать в виде обыкновенной дроби.