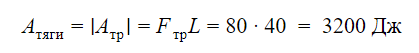Как называется единица измерения работы
Механическая работа и мощность
Определение механической работы
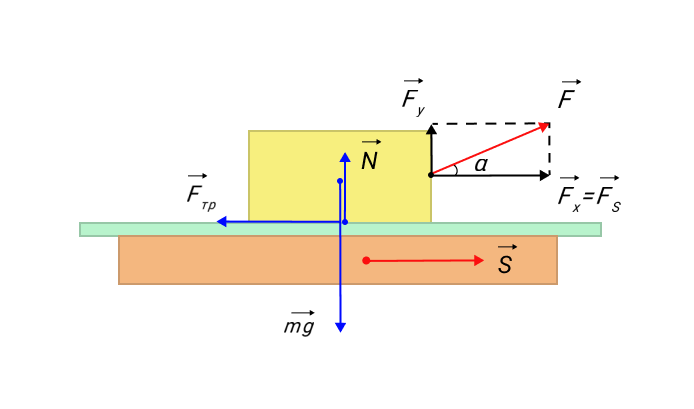
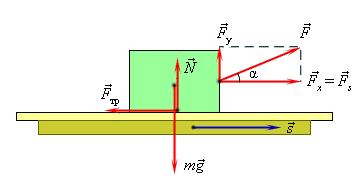
Данное определение рассматривается на рисунке 1.
Формула работы записывается как,
Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.
Рисунок 1. Работа силы F → : A = F s cos α = F s s
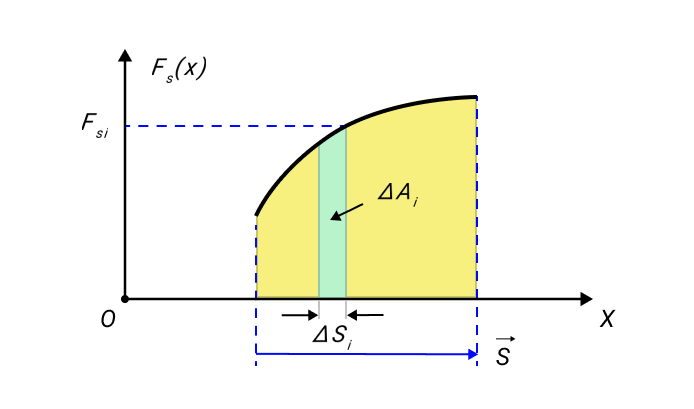
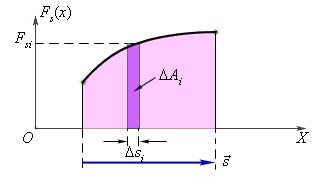
При проекции F s → силы F → на направление перемещения s → сила не остается постоянной, а вычисление работы для малых перемещений Δ s i суммируется и производится по формуле:
Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком F s ( x ) рисунка 2.
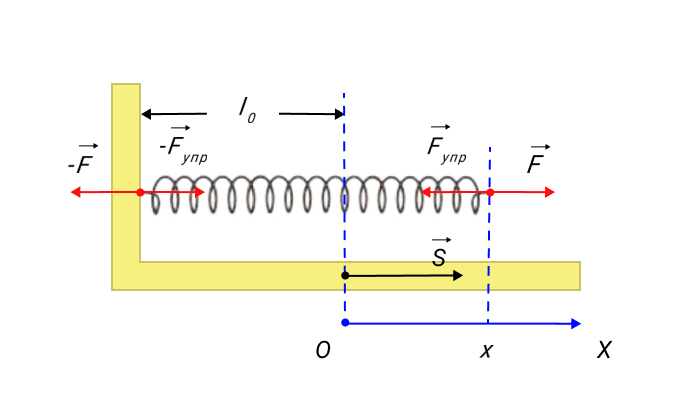
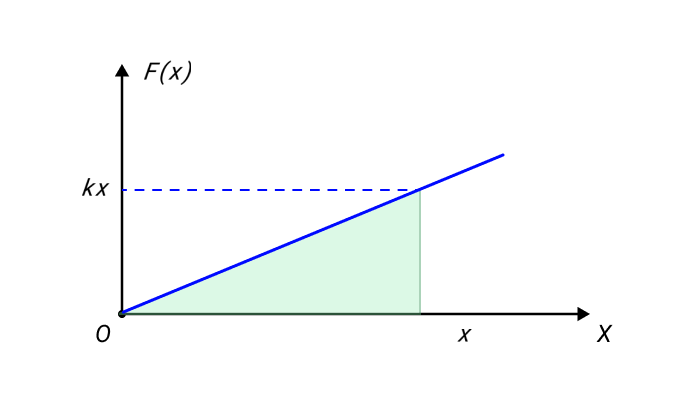
Зависимость модуля внешней силы от координат x можно изобразить на графике с помощью прямой линии.
Рисунок 4. Зависимость модуля внешней силы от координаты при растяжении пружины.
Из выше указанного рисунка возможно нахождение работы над внешней силой правого свободного конца пружины, задействовав площадь треугольника. Формула примет вид
Если на тело действует несколько сил, то их общая работа равняется сумме всех работ, совершаемых над телом. Когда тело движется поступательно, точки приложения сил перемещаются одинаково, то есть общая работа всех сил будет равна работе равнодействующей приложенных сил.
Мощность
Мощностью называют работу силы, совершаемую в единицу времени.
Помимо Ватта, существуют и внесистемные единицы измерения мощности. Например, 1 лошадиная сила примерна равна 745 Ваттам.
Подготовка к ЕГЭ по физике
Материалы для подготовки к ЕГЭ по физике
Раздел «Программное обеспечение компьютерных сетей»
Материал для изучения дисциплины «Программное обеспечение компьютерных сетей»
Раздел «Информатика»
Материалы для изучения дисциплины «Информатика»
Раздел «Физика»
Надеюсь, данный раздел поможет Вам эффективно и интересно изучать физику.
Учите физику!
Как сказал.
Все знают, что это невозможно. Но вот приходит невежда, которому это неизвестно — он-то и делает открытие.
Альберт Эйнштейн
Вопросы к экзамену
Для всех групп технического профиля

Законы и формулы
Я учу детей тому, как надо учиться
Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.
Новости и знаменательные даты
Вопрос 9
Механическая работа и мощность. Единицы измерения работы и мощности.
Краткий ответ
Механическая работа – это скалярная величина, равная произведению модуля силы, действующей на тело, на модуль перемещения и на косинус угла между вектором силы и вектором перемещения (или скорости).
Развернутый ответ
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Если на тело действует сила и тело под действием этой силы перемещается, то говорят, что сила совершает работу.
Механическая работа – это скалярная величина, равная произведению модуля силы, действующей на тело, на модуль перемещения и на косинус угла между вектором силы и вектором перемещения (или скорости).
В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.
[1 Дж=1 Н·м]
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α 1) Если направление силы совпадает с направлением движения тела, т.е.α = 0, cos α = 1 то
2) Если сила направлена перпендикулярно к направлению движения тела, т.е. α = 90º, cos α = 0 то
3) Если угол между направлением силы и направлением движения тупой, т.е. α > 90º, cos α A=-F·S·cosa
Например, работа силы сопротивления отрицательна.
Графически работа определяется по площади криволинейной фигуры под графиком F s( x)
Мощность N – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.
Связь между мощностью и скоростью при равномерном движении:
N=A/t так как A=FScosα тогда N=(FScosα)/t, но S/t = v следовательно
В технике используются единицы работы и мощности:
1 Вт·с = 1 Дж; 1Вт·ч = 3,6·10 3 Дж; 1кВт·ч = 3,6·10 6 Дж
Механическая работа
Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.
Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.
Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.
Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.
Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.
Механическая работа
А = FScosα
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
α — угол между векторами силы и перемещения []
Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.
Для совершения работы необходимы два условия:
Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Полезная и затраченная работа
Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».
Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.
Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.
Потенциальная энергия
Еп = mgh
m — масса тела [кг]
g — ускорение свободного падения [м/с 2 ]
h — высота [м]
На планете Земля g ≈ 9,8 м/с 2
Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
И как же достоверно определить, какая работа полезная, а какая затраченная?
Все очень просто! Задаем два вопроса:
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).
Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
Мощность
На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность
N = A/t
N — мощность [Вт]
A — механическая работа [Дж]
t — время [с]
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.
Также для мощности справедлива другая формула:
Мощность
N = Fv
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.
Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:
Мощность
N = Fvcosα
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
α — угол между векторами силы и скорости []
Примеры решения задач
Задача 1
Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:
Решение
Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.
Ответ: 3.
Задача 2
Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Решение
Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:
Ответ: 3200 Дж.
Задача 3
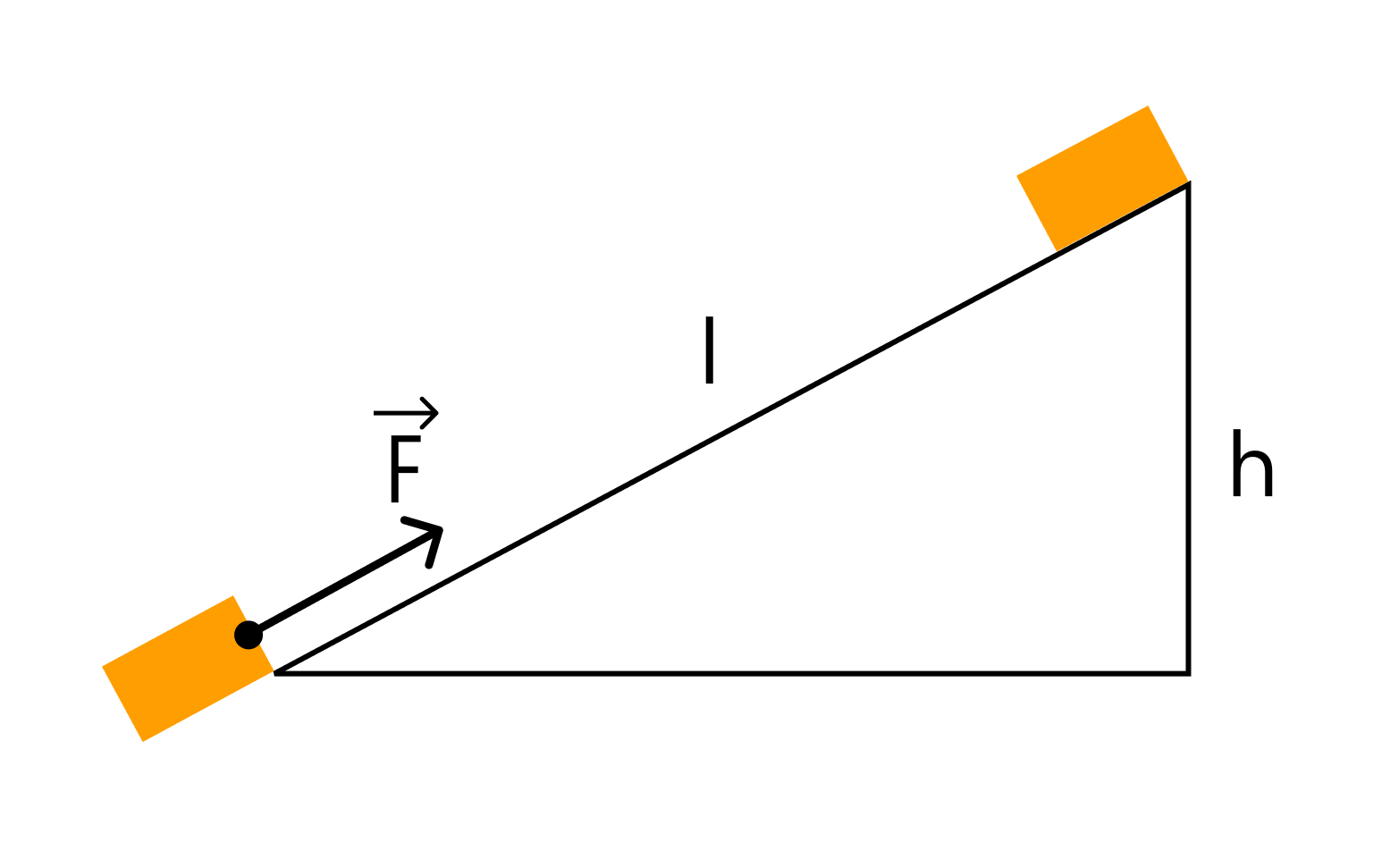
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?
Решение
В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:
A = Fl = 30 * 5 = 150 Дж
Ответ: 150 Дж.
Задача 4
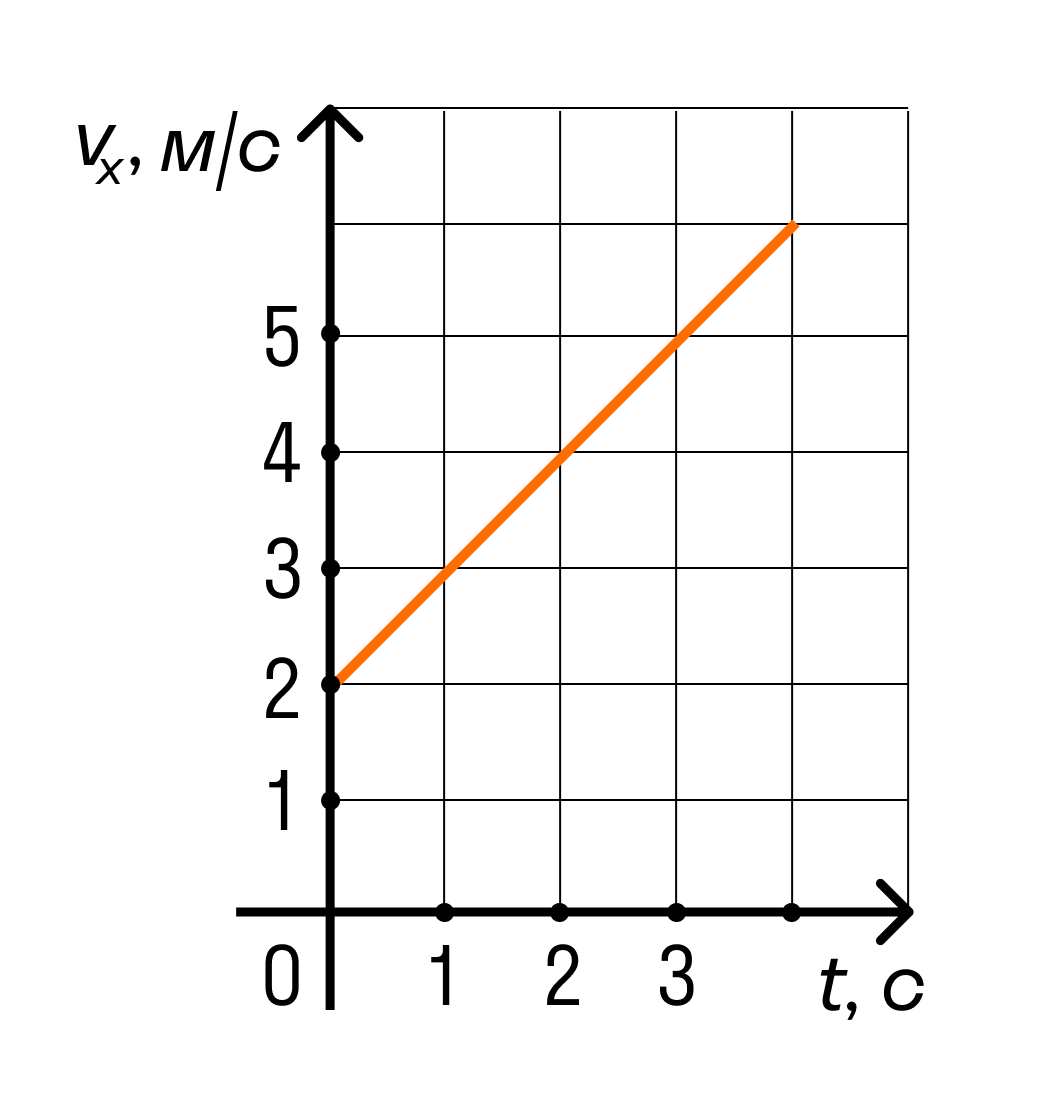
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение
На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.
Мощность можно найти по формуле N = Fv.
N = FV = 2×5 = 10 Вт
Ответ: 10 Вт.
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!
Ньютон (единица измерения)
Единица названа в честь английского физика Исаака Ньютона, открывшего законы движения и связавшего понятия силы, массы и ускорения. В своих работах, однако, Исаак Ньютон не вводил единиц измерения силы и рассматривал её как абстрактное явление. [1] Измерять силу в ньютонах стали спустя более чем два века после смерти великого учёного, когда была принята система СИ.
Содержание
Связь с другими единицами
С другими единицами измерения силы ньютон связывают следующие выражения:
Кратные и дольные единицы
Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 10 1 Н | деканьютон | даН | daN | 10 −1 Н | дециньютон | дН | dN |
| 10 2 Н | гектоньютон | гН | hN | 10 −2 Н | сантиньютон | сН | cN |
| 10 3 Н | килоньютон | кН | kN | 10 −3 Н | миллиньютон | мН | mN |
| 10 6 Н | меганьютон | МН | MN | 10 −6 Н | микроньютон | мкН | µN |
| 10 9 Н | гиганьютон | ГН | GN | 10 −9 Н | наноньютон | нН | nN |
| 10 12 Н | тераньютон | ТН | TN | 10 −12 Н | пиконьютон | пН | pN |
| 10 15 Н | петаньютон | ПН | PN | 10 −15 Н | фемтоньютон | фН | fN |
| 10 18 Н | эксаньютон | ЭН | EN | 10 −18 Н | аттоньютон | аН | aN |
| 10 21 Н | зеттаньютон | ЗН | ZN | 10 −21 Н | зептоньютон | зН | zN |
| 10 24 Н | йоттаньютон | ИН | YN | 10 −24 Н | йоктоньютон | иН | yN |
| применять не рекомендуется | |||||||
Примеры
| Описание | Значение |
|---|---|
| Сила, действующая на электрон со стороны ядра атома водорода | 3,6967·10 −10 Н |
| Сила, которая давила бы на солнечный парус спутника Космос 1 в случае его успешного запуска | 3,5343·10 −3 Н |
| Вес тела массой 102 г (т. е. сила гравитации, действующая на это тело на поверхности Земли) | 1 Н |
| Сила притяжения, действующая на человека массой 70 кг | 686 Н |
| Суммарная сила давления воздуха на тело человека [2] (при нормальных условиях) | 202 650 Н |
Примечания
Полезное
Смотреть что такое «Ньютон (единица измерения)» в других словарях:
Ньютон (единица) — Ньютон (обозначение: Н, N) единица измерения силы в системе СИ. 1 ньютон равен силе, сообщающей телу массой 1 кг ускорение 1 м/с² в направлении действия силы. Таким образом, 1 Н = 1 кг·м/с². Единица названа в честь английского физика Исаака… … Википедия
Единица измерения Сименс — Сименс (обозначение: См, S) единица измерения электрической проводимости в системе СИ, величина обратная ому. До Второй мировой войны (в СССР до 1960 х годов) сименсом называлась единица электрического сопротивления, соответсвующая сопротивлению … Википедия
Тесла (единица измерения) — У этого термина существуют и другие значения, см. Тесла. Тесла (русское обозначение: Тл; международное обозначение: T) единица измерения индукции магнитного поля в Международной системе единиц (СИ), численно равная индукции такого… … Википедия
Зиверт (единица измерения) — Зиверт (обозначение: Зв, Sv) единица измерения эффективной и эквивалентной доз ионизирующего излучения в Международной системе единиц (СИ), используется с 1979 г. 1 зиверт это количество энергии, поглощённое килограммом… … Википедия
Беккерель (единица измерения) — У этого термина существуют и другие значения, см. Беккерель. Беккерель (обозначение: Бк, Bq) единица измерения активности радиоактивного источника в Международной системе единиц (СИ). Один беккерель определяется как активность источника, в… … Википедия
Сименс (единица измерения) — У этого термина существуют и другие значения, см. Сименс. Сименс (русское обозначение: См; международное обозначение: S) единица измерения электрической проводимости в Международной системе единиц (СИ), величина обратная ому. Через другие… … Википедия
Паскаль (единица измерения) — У этого термина существуют и другие значения, см. Паскаль (значения). Паскаль (обозначение: Па, международное: Pa) единица измерения давления (механического напряжения) в Международной системе единиц (СИ). Паскаль равен давлению… … Википедия
Грей (единица измерения) — У этого термина существуют и другие значения, см. Грей. Грей (обозначение: Гр, Gy) единица измерения поглощённой дозы ионизирующего излучения в Международной системе единиц (СИ). Поглощённая доза равна одному грею, если в результате… … Википедия
Вебер (единица измерения) — У этого термина существуют и другие значения, см. Вебер. Вебер (обозначение: Вб, Wb) единица измерения магнитного потока в системе СИ. По определению, изменение магнитного потока через замкнутый контур со скоростью один вебер в секунду наводит в… … Википедия
Генри (единица измерения) — У этого термина существуют и другие значения, см. Генри. Генри (русское обозначение: Гн; международное: H) единица измерения индуктивности в Международной системе единиц (СИ). Цепь имеет индуктивность один генри, если изменение тока со скоростью… … Википедия
Единица измерения работы
Слово «работа» имеет несколько значений: результат труда, действие механизма, любая деятельность или её готовый продукт. В чём измеряется работа, можно говорить лишь после того, как станет понятно, о каком процессе идёт речь. В физике рассматриваются такие её виды, как: механическая, термодинамическая или работа выхода – количество энергии, приданное отрицательно заряженной частице (электрону) для удаления его из твёрдого вещества.

Работа как составная часть процесса
Определение
Когда на тело действует некоторая сила, заставляющая его проделать путь в определённом направлении, есть смысл говорить о совершённой им полезной работе. Это физическая мера, в механике равна скалярному значению силы, влияющей на тело.
Важно! Работа напрямую зависит от того, куда и в какую сторону действует сила, от её количественного значения, а также от того, как далеко переместится объект, попавший под воздействие этой силы.
Работа силы, приложенной к материальной точке
Сила F→ постоянной величины и направления воздействует на точку. Траектория движения точки прямолинейная. Соответствующая A такой силы будет равна произведению её проекции F→ на направление перемещения (касательную) и длину элементарного смещения точки:
где:
Как видно из формулы, это произведение скалярное.
Внимание! При таких вычислениях F→ пребывает неизменной в промежутке времени, за которое рассчитывается необходимая работа.
Такая формула справедлива только для прямолинейного перемещения точки и F→ = const. В противном случае рассчитать работу поможет интеграл:
тут интеграл второго рода является криволинейным и суммирует все перемещения по кривой. При этом необходимо принимать перемещения ds→ конечными, в итоге длину каждого сделать стремящейся к нулю.

Приложение силы к реальной точке
Работа сил, приложенных к системе материальных точек
Возникает, когда необходимо измерить значение для сил, влияющих на систему реальных точек. Её можно получить путём сложения работ для сил, способствующих передвижению каждой точки такой системы.
Для случаев, когда тело не представляет собой систему, состоящую из дискретных точек, применяют его мысленное разбиение на элементы. Бесконечно маленький размер такого элемента позволяет считать его материальной точкой. Применение интегрирования вместо дискретной суммы даст возможность рассчитать значение A.
К сведению. Производить математические вычисления допустимо для нахождения работы не только одной определённой силы, но и для любого количества подобных сил, приложенных к точке или системе точек.
Средняя мощность
Если: P — Средняя мощность (Ватт) А(W) — Работа (Джоуль) t — Время затраченное на совершение работы (секунд) то
Примечание: Если работа пропорциональна времени, W
t, то мощность постоянна.
Каждая машина потребляет большую мощность, чем отдает, поскольку в ней происходят потери мощности (за счет трения, сопротивления воздуха, нагревания и т.д.)
Коэффициент полезного действия представляет собой отношение полезной работы к ззатраченой работе.
Кинетическая энергия
В чем измеряется освещенность
Это часть полной энергии, определяющая энергетику движения. В системе СИ измеряется в джоулях (Дж), в СГС – в эргах (эрг).
Как связать понятие работы с кинетической энергией? Формула кинетической энергии имеет вид:
В этой формуле физическая величина Ek равна 1/2 от массы тела, умноженной на скорость этого тела в квадрате.

Кинетическая энергия
Далее отображается работа сил, воздействующих на точку при помощи 2-го закона Ньютона. Формула закона позволяет через ускорение (а) выразить силу (F):
Оперируя с кинематическими величинами и обратив внимание на формулу А = F*s, пробуют выразить желаемую взаимосвязь.
Случай прямолинейного ускоренного движения, где скорость и перемещение можно выразить формулой:
Следует подставить значение величины перемещения s и F в формулу работы:
А = m*a*(v22-v21)/2a = m*v22/2 – m*v21/2.
Уменьшаемое или вычитаемое, отображаемые во второй части полученного равенства, имеют общий вид:
Это есть кинетическая энергия, её обычно обозначают – Ek.
Из всего этого следует, что работа, выполняемая над телом, равнодействующих сил, соответствует изменению Ek.
Следует запомнить! Когда сила давит на тело сонаправленно его движению, совершаемая ею работа положительна, и Ek > 0. Когда она приложена навстречу движению тела, тогда Ek 
Второй закон Ньютона
Потенциальная энергия
В чем измеряется свет
Эта физическая характеристика является частью полной механической энергии. Описывает расположение тела в силовом поле (источнике силы). Причём эта величина может давать оценку только для целой системы. Она бесполезна для характеристики отдельных точек. При этом оценивается не величина, а ее изменение.
Единицей измерения является Дж или Эрг. Наиболее часто применяемые графические обозначения – U, Ep, W.
Различают следующие типы потенциальной энергии:
Для тела, расположенного поблизости от земной поверхности, формула имеет вид:
Уровень нуля можно выбирать произвольно.
Электрически заряженная материальная точка, имеющая потенциал φ(r→), находясь в зоне электростатического поля, обладает потенциальной энергией Ер. Она вычисляется с помощью выражения:
где qp – электрический заряд, которым эта точка обладает.
В механических системах при упругих деформациях тела разные его точки взаимодействуют между собой. Такие взаимодействия можно охарактеризовать потенциальной энергией.
Упругая деформация может быть записана как:
Здесь k – это жёсткость (упругость), ∆x – величина смещения от равновесного положения.
Работа в термодинамике
В чем измеряется работа сил в термодинамике? Термодинамика рассматривает процессы преобразования системы, в результате которых меняется объём. При этом внутреннее изменение энергии тела есть работа. Лучше всего разобрать это на примере воздействия газа на поршень. Пусть газ давит на поверхность поршня с силой F→’. Она, согласно 3-му закону Ньютона, направлена в противоположную сторону той силе, с которой поршень воздействует на газ. Это значит, F→’ = – F→.
Единица измерения силы тока
Под давлением газа (p) поршень начинает совершать перемещение ∆h. В случае, если оно мало, то можно говорить о том, что p = const. Тогда работа будет равна A’ = F’*∆h. Можно подставить сюда значение F’= p*S, где S – площадь поверхности, на которую давит газ. После этого выражение примет вид:
где ∆V – изменение объёма.
Важно! Работа положительная, если газ расширяется. Это обусловлено тем, что поршень движется в ту же сторону, куда направлена F→’. При сжимании газа его работа имеет отрицательное значение, потому как поршень перемещается в противоположную от F→’ сторону.

Работа в термодинамике
Определение и формула работы
В том случае, если под воздействием силы происходит изменение модуля скорости движения тела, то говорят о том, что сила совершает работу
. Считают, что если скорость увеличивается, то работа является положительной, если скорость уменьшается, то работа, которую совершает сила – отрицательна. Изменение кинетической энергии материальной точки в ходе ее движения между двумя положениями равно работе, которую совершает сила:
$$A=\Delta E_
Действие силы на материальную точку можно охарактеризовать не только с помощью изменения скорости движения тела, но при помощи величины перемещения, которое совершает рассматриваемое тело под действием силы ($\bar
Работа силы в теоретической механике
При изучении в теоретической механике преобразований любых форм механического движения в иные типы движения используют понятие работы силы. При расчётах подразумевают, что и направление, и модуль этой силы F постоянны, выражение имеет вид:
A = F→*s→ = F*s*cos(F→,s→) = F*s*cos α.
От угла α зависит знак А, от направления зависит величина работы:
Отдельными случаями в теоретической механике рассматривают воздействие сил при перемещениях точек по криволинейным траекториям и их вращениях по оси.
Формула механической работы
Представим, что нам нужно поднять все тот же шар не на 50 см, а на 100 см. Необходимо совершить работу, чтобы поднять его сначала на первую половину дистанции, а затем на вторую. Всякий раз будет совершаться одинаковая работа, но общая работа будет в два раза больше. Значит, работа прямо пропорциональна расстоянию перемещения тела. Поэтому физики договорились обозначить величину F*s буквой А и назвать ее работой силы. Выражение F*s как раз и будет прямо пропорционально силе и перемещению тела.
A=F*s — это формула работы в физике. A — искомая величина силы, приложенной к телу, а s — путь, пройденный телом. Однако бывают ситуации, когда сила приложена к телу, а оно не перемещается. В нашем третьем случае тело перемещается в том же направлении, в котором приложена сила. Поэтому точнее будет сказать, что s — это перемещение тела в направлении действия силы. Сформулируем определение: работа в физике — это величина, равная произведению модуля силы на перемещение тела в направлении действия силы.
Размерность и единицы
Работа, совершаемая в процессах физики, имеет почти одинаковые обозначения, измерять её можно, зная единицы.
Основная единица измерения работы – 1 джоуль (Дж). Он равен:
1 Дж = 1 Н*м = 1 кг*м²/с².
1 эрг = 1 г*см²/с² = 1 дин*см = 10−7 Дж.
Работа двигателя внутреннего сгорания соразмерна тяге одной лошади. Одна лошадиная сила равна поднятию лошадью тяжести весом 75 кг. Хотя это не совсем верно. В данном случае речь идёт о мощности, это не что иное, как работа двигателя, выполняемая им ежесекундно.
(В*А*с) – это тоже единица измерения, работа, совершаемая электрическим током при перемещении заряженных зарядов по цепи за единицу времени. Сама формула пишется так:

Виды А некоторых сил
Сила трения, которая не только изнашивает трущиеся детали, но и помогает движению транспорта, также совершает определённую работу. Её выполняет и сила тяжести. На определение величины работы тех или иных сил влияют условия, при которых она совершается.
Единицы измерения.
Перевод единиц измерения работы.
Калькулятор работы. Перевод единиц измерения работы (Дж, кДж, МДж, кал, ккал, Мкал, Гкал, эрг, кВт*ч и т.д.)
Введите количество работы (AA)
Результат перевода единиц измерения работы (AA)
Результаты работы калькулятора работы при переводе в другие единицы измерения работы:
Примеры результатов работы калькулятора работы:
/ 100 кал = 23884600000 эрг
//
100 кал = 0.0085985 кВт*ч
//
10 кал = 0.01 ккал
//
100 кал = 23884600000 эрг
//
100 кал = 0.00041868 МДж
//
100 кал = 0.1 ккал
/