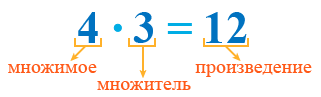Как называется пример на умножение
Умножение
В этом разделе познакомимся с умножением и узнаем, что сложение одинаковых слагаемых можно заменить умножением.
Например, 6 + 6 + 6 + 6 = 24 можно записать по-другому: 6 • 4 = 24
Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.
Первое число при умножении показывает, какое слагаемое повторяют несколько раз.
Второе число при умножении показывает, сколько раз повторяют это слагаемое.
Результат умножения показывает, какое число получается.
6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24
Числа при умножении
Результат умножения, или Произведение
Чтение числовых выражений
Этот пример можно прочитать по-разному.
Умножение на 1
4 • 1 = 4, потому что это значит, что число 4 повторяют только 1 раз.
23 • 1 = 23, потому что это значит, что число 23 повторяют только 1 раз.
Умножение на 0
8 • 0 = 0, потому что это значит, что число 8 повторяют 0 раз.
26 • 0 = 0, потому что это значит, что число 26 повторяют 0 раз.
Умножение на 10
8 • 10 = 80, потому что число 8 повторяют 10 раз.
15 • 10 = 150, потому что число 15 повторяют 10 раз.
Связь деления и умножения
8 • 3 = 24, потому что 8 повторяют 3 раза.
24 : 3 = 8, потому что в 24 по 3 содержится 8 раз.
24 : 8 = 3, потому что в 24 по 8 содержится 3 раза.
В несколько раз больше
Решим задачу:
В магазине было 2 лисички, а котят в 4 раза больше. Сколько было котят?
Это значит, что котят было 4 раза по 2.
Заменяем сложение умножением и получаем:
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях:
Умножение натуральных чисел
Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.
Пример. Во дворе посадили 3 ряда ёлок, по 4 ёлки в каждом ряду. Сколько ёлок посадили во дворе?
Чтобы ответить на этот вопрос, надо найти сумму 3 слагаемых, каждое из которых равно 4.
Складывая 3 раза по 4 ёлки, мы получим общее количество ёлок во всех трёх рядах.
Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.
Для записи умножения используется знак х (косой крест) или · (точка), который ставится между числами. Например:
Эта запись означает, что 4 надо умножить на 3. Справа от записи умножения ставится знак = (равно), после которого записывается полученный результат:
Умножение – это краткая запись сложения одинаковых слагаемых.
Пример. Умножить 6 на 5 — это значит найти сумму пяти слагаемых, каждое из которых равно шести:
Сократим запись, заменив сложение на умножение:
Оба выражения равны:
6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,
но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.
Множимое, множитель и произведение
Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:
4 — это множимое, 3 — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.
Произведение — это число, которое получается в результате умножения. Например, в записи:
12 — это произведение. При этом сама запись 4 · 3 тоже называется произведением.
Множимое и множитель иначе называются множителями или сомножителями.
Проверка умножения
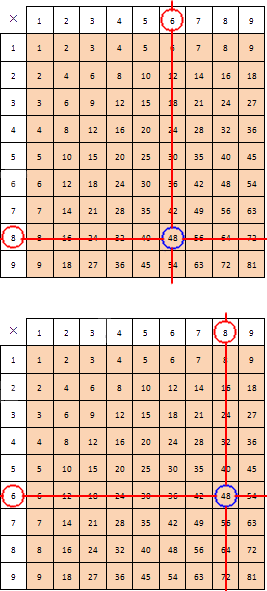
Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.
Умножение натуральных чисел: правила, примеры, решения
Имея общее представление об умножении натуральных чисел и их свойств, легче понять принцип выполнений действий над ними. Мы разберем правила, по которым производится умножение натуральных чисел. Весь материал имеет конкретные примеры и подробные объяснения. Совершим проверки результатов для того, чтобы сверить полученные на выходе числа.
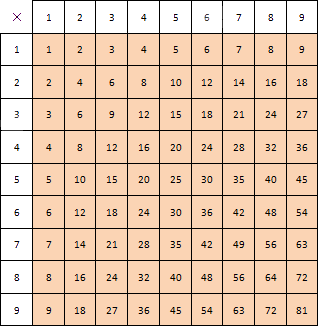
Таблица умножения
| 1 · 1 = 1 | 2 · 1 = 2 | 3 · 1 = 3 |
| 1 · 2 = 2 | 2 · 2 = 4 | 3 · 2 = 6 |
| 1 · 3 = 3 | 2 · 3 = 6 | 3 · 3 = 9 |
| 1 · 4 = 4 | 2 · 4 = 8 | 3 · 4 = 12 |
| 1 · 5 = 5 | 2 · 5 = 10 | 3 · 5 = 15 |
| 1 · 6 = 6 | 2 · 6 = 12 | 3 · 6 = 18 |
| 1 · 7 = 7 | 2 · 7 = 14 | 3 · 7 = 21 |
| 1 · 8 = 8 | 2 · 8 = 16 | 3 · 8 = 24 |
| 1 · 9 = 9 | 2 · 9 = 18 | 3 · 9 = 27 |
| 4 · 1 = 4 | 5 · 1 = 5 | 6 · 1 = 6 |
| 4 · 2 = 8 | 5 · 2 = 10 | 6 · 2 = 12 |
| 4 · 3 = 12 | 5 · 3 = 15 | 6 · 3 = 18 |
| 4 · 4 = 16 | 5 · 4 = 20 | 6 · 4 = 24 |
| 4 · 5 = 20 | 5 · 5 = 25 | 6 · 5 = 30 |
| 4 · 6 = 24 | 5 · 6 = 30 | 6 · 6 = 36 |
| 4 · 7 = 28 | 5 · 7 = 35 | 6 · 7 = 42 |
| 4 · 8 = 32 | 5 · 8 = 40 | 6 · 8 = 48 |
| 4 · 9 = 36 | 5 · 9 = 45 | 6 · 9 = 54 |
| 7 · 1 = 7 | 8 · 1 = 8 | 9 · 1 = 9 |
| 7 · 2 = 14 | 8 · 2 = 16 | 9 · 2 = 18 |
| 7 · 3 = 21 | 8 · 3 = 24 | 9 · 3 = 27 |
| 7 · 4 = 28 | 8 · 4 = 32 | 9 · 4 = 36 |
| 7 · 5 = 35 | 8 · 5 = 40 | 9 · 5 = 45 |
| 7 · 6 = 42 | 8 · 6 = 48 | 9 · 6 = 54 |
| 7 · 7 = 49 | 8 · 7 = 56 | 9 · 7 = 63 |
| 7 · 8 = 56 | 8 · 8 = 64 | 9 · 8 = 72 |
| 7 · 9 = 63 | 8 · 9 = 72 | 9 · 9 = 81 |
Это и есть таблица умножения. Все результаты сгруппированы для удобного дальнейшего применения. Таблица сложения натуральных чисел выглядит подобным образом. Она предоставлена ниже.
Умножение трех и более количества чисел
Мы дали определение понятию умножения двух чисел. Теперь поговорим об умножении трех и более имеющихся чисел. Таким образом, в такой ситуации применимо сочетательное свойство умножения натуральных чисел.
Обычно скобки опускаются при умножении. Произведение нескольких трех и более чисел без скобок приводит к последовательной замене двух соседних множителей до получения необходимого результата. Скобки могут быть расставлены произвольно, так как итог произведения не изменится.
Порядок следования множителей не влияет на результат. Множители могут быть записаны в любом порядке. Это следует из свойств умножения натуральных чисел.
Чтобы избежать это, необходимо поменять слагаемые местами, иначе расставить скобки.
При перемене мест множителей можно производить наиболее удобные комбинирования для вычисления. Рассмотрим задание, где решение приводит к умножению нескольких чисел.
Каждая коробка имеет по 3 предмета. В ящики положили 2 коробки. Какое количество предметов будет в 4 ящиках?
Решение
Нам дано, что в одном ящике 2 коробки, а в них соответственно по 3 предмета.
Тогда в одном ящике 3 · 2 = 6 предметов. Отсюда получим, что в 4 ящиках 6 · 4 = 24 предмета. Можно рассуждать иным образом. Один ящик вмещает в себя 2 коробки, отсюда в 4 ящиках 2 · 4 = 8 коробок. Каждая из коробок имеет 3 предмета, тогда имеем, что 8 коробок содержат 3 · 8 = 24 предмета.
При умножении трех и более чисел действия производятся последовательно. Используя переместительное и сочетательное свойства умножения, разрешается менять местами множителями и заменять их двумя другими умножаемыми числами.
Умножение суммы на натуральное число и наоборот
Благодаря распределительному свойству умножения сложение и умножение связаны. Это помогает в изучении сложения и умножения. Свойство способствует углубиться в изучение всех действий.
Отсюда следует, что произведение суммы нескольких чисел и данного числа равна сумме произведений каждого из слагаемых с данным числом. Это правило применимо при умножении на заданное число.
Можно было сделать вычисления иначе, тогда следовало посчитать сумму, после чего умножение. Этот случай менее удобен, так как умножение двухзначного числа 7 + 2 + 3 + 8 + 8 = 28 на 3 мы пока не выполняли. Умножение двухзначных чисел – это тема, показанная в разделе умножения многозначного и однозначного натуральных чисел.
Используя переместительное свойство, мы можем переформулировать правило умножения суммы чисел на заданное число таким образом: произведение данного числа и суммы нескольких чисел равняется сумме произведений данного числа и каждого из слагаемых. Это правило умножения данного числа на заданную сумму.
Рассмотрим конкретный пример, где умножение решение сводится к умножению суммы чисел на данное число.
В коробке находятся по 3 красных, 7 зеленых и 2 синих предмета. Какой количество предметов имеется во всех четырех коробках?
Ответ: 48 предметов.
Умножение натурального числа на 10, 100, 1000 и так далее
Таким же образом можно прийти к следующим неравенствам:
Выходит, что десяток десятков – это сотня, то 10 · 10 = 100 ;
рассмотрим пример для формулировки правила умножения произвольного натурального числа на 10.
Чтобы быстрее подсчитать, необходимо представить число 7032 в виде суммы разрядных слагаемых.
В качестве примера запишем:
Умножение многозначного и однозначного натуральных чисел
Имея навыки для выполнения умножения, разберем все правила на примере.
Используя правило умножения суммы на число, получим, что:
Чтобы закрепить материал, необходимо рассмотреть пример умножения.
Умножение двух многозначных натуральных чисел
Умножение двух многозначных натуральных чисел производится таким образом, что один из множителей раскладывается по разрядам, после этого применяют правило умножения на сумму. Изучение предыдущих статей позволит быстрее разобраться с имеющимся разделом.
Решение
41 · 3 = ( 40 + 1 ) · 3 = 40 · 3 + 1 · 3 = ( 4 · 10 ) · 3 + 1 · 3 = ( 3 · 4 ) · 10 + 1 · 3 = 12 · 10 + 3 = 120 + 3 = 123 ; 41 · 8 = ( 40 + 1 ) · 8 = 40 · 8 + 1 · 8 = ( 4 · 10 ) · 8 + 1 · 8 = ( 8 · 4 ) · 10 + 1 · 8 = 32 · 10 + 8 = 320 + 8 = 328 ; 41 · 6 = ( 40 + 1 ) · 6 = 40 · 6 + 1 · 6 = ( 4 · 10 ) · 6 + 1 · 6 = ( 6 · 4 ) · 10 + 1 · 6 = 24 · 10 + 6 = 240 + 6 = 246
( 41 · 3 ) · 1 000 + ( 41 · 8 ) · 100 + 41 · 6 = 123 · 1 000 + 328 · 100 + 246 = 123 000 + 32 800 + 246
Вычислим сумму натуральных чисел:
123 000 + 32 800 + 246 = 156 046
Теперь умеем умножать два любых натуральных числа.
Проверка результата умножения натуральных чисел
Умножение всегда требует проверки. Она производится при помощи деления по правилу: полученное произведение делят на один из множителей. Если полученное число равно одному из множителей, тогда вычисление произведено правильно. Если нет, то допущена ошибка.
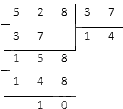
Если получим число, равное одному из множителей, тогда задание решено верно.
Ответ: проверка показала, что умножение было выполнено неверно.
Умножение натуральных чисел
Я сперва покажу на примере, для чего нужно умножение, а после дам определение умножения и подробно расскажу об этом действии.
Допустим, мы хотим купить 14 тетрадей по 22 рубля каждая. Планируя покупку, нам нужно знать, сколько мы заплатим за всю покупку?
Чтобы ответить на этот вопрос, нам нужно сложить стоимость каждой тетради, которую мы хотим купить. А, так мы запланировали покупку 14 тетрадей, тогда мы складываем 22 рубля 14 раз, то есть, находим сумму 14 слагаемых, каждое из которых равно 22 :
22+22+22+22+22+22+22+22+22+22+22+22+22+22=308 (то есть, 308 рублей).
Если размер и количество одинаковых слагаемых небольшие, мы без особого труда можем найти их сумму. Но что же делать, если слагаемые многозначные и их количество велико?
Умножение – это арифметическое действие сложения определенного количества одинаковых слагаемых.
Действие умножение – это частный случай действия сложение.
Число, которое является повторяющимся слагаемым, называется множимое (то, что множится, умножается).
Число, которое указывает на количество одинаковых слагаемых, называется множитель.
Множимое и множитель имеют общее название – сомножители.
Результат действия умножения называется произведением.
22 ∙14=308,
22x14=308,
22*14=308.
При записи от руки действие умножение принято обозначать при помощи точки, косой крест используется в основном при печати, а звездочка – в компьютерном наборе. Но даже и во время компьютерного набора грамотнее использовать точку или косой крест (букву х).
Прочитать действие умножения и результат можно такими способами:
Компоненты действия умножение для двух сомножителей:
Компоненты умножения для трех сомножителей и более:
Основные свойства умножения
Поскольку действие умножение является частным случаем действия сложение, то основные свойства сложения распространяются и на умножение.
Законы умножения и их следствия
Умножение обладает такими основными свойствами, называемые законами умножения, из которых вытекают остальные свойства и следствия:
Переместительный закон умножения.
Произведение двух или нескольких сомножителей от изменения их порядка не меняется.
Это значит, что значение произведения не зависит от порядка перемножения сомножителей, то есть, от порядка выполнения действия умножение.
Для двух сомножителей мы можем записать переместительный закон умножения в общем виде так:
ab=ba.
Допустим, нам нужно подсчитать количество отделений в шкафу (рис. 1).
Это свойство также верно для трех и более сомножителей.
К примеру, нам нужно подсчитать количество отделений в двух одинаковых шкафах (рис. 2).
5 ∙3+5 ∙3 =5 ∙3 ∙2.
15+15=15 ∙2,
30=30.
3 ∙5+3 ∙5=3 ∙5 ∙2,
15+15=15 ∙2,
30=30.
Значит, 5 ∙3 ∙2=3 ∙5 ∙2=30.
Поэтому, для трех сомножителей переместительный закон умножения в общем виде выглядит так:
abc=acb=bac=bca=cab=cba.
Сочетательный закон умножения.
Результат умножения трех и более чисел не изменяется, если любые из этих сомножителей заменить их произведением.
Следовательно, мы можем группировать множители между собой каким угодно образом, и выполнять действие умножения с этими группами.
В общем виде для трех сомножителей сочетательный закон умножения можно выразить так:
abc=a(bc)=(ab)c=b(ac).
Этот закон можно назвать следствием переместительного закона умножения.
Так, при подсчете количества отделений в двух шкафах на рисунке 2, мы можем сперва найти число отделений в одном шкафу, а потом умножить результат на 2 :
(5 ∙3) ∙2=15 ∙2=30,
(3 ∙5) ∙2=15 ∙2=30,
а можем сперва найти общее количество рядов отделений в обоих шкафах, а после умножить их на количество отделений в ряду:
(3 ∙2) ∙5=6 ∙5=30.
Как видите, результат во всех случаях одинаковый.
Особые случаи умножения: умножение единицы и нуля
Если в произведении двух чисел один из сомножителей единица, то произведение равно второму сомножителю:
a ∙1=1 ∙a=a.
А при умножении единицы на любое число (например, 1 ∙ 7 ) мы находим сумму семи единиц, то есть, то количество единиц, из которых состоит данное число. Следовательно, сумма этих единиц равна самому данному числу :
1+1+1+1+1+1+1=7.
Если в произведении любого количества сомножителей одним из сомножителей является нуль, то и произведение равно нулю:
a∙b∙0=0∙a∙b=a∙0∙c=0.
Умножение однозначных чисел
Умножение двух однозначных натуральных чисел a и b – это нахождения суммы b слагаемых, каждое из которых равно числу a, и при этом a и b являются натуральными числами.
Для облегчения вычисления, были посчитаны результаты умножения всех однозначных чисел друг на друга, и сведены в специальные таблицы умножения.
Умножение многозначного числа на однозначное
900+80+5+900+80+5+900+80+5+900+80+5.
Воспользуемся законами сложения и сгруппируем одинаковые слагаемые этого выражения вместе:
900+900+900+900+80+80+80+80+5+5+5+5,
(900+900+900+900)+(80+80+80+80)+(5+5+5+5).
Суммы в скобках мы можем заменить на произведение одинаковых слагаемых и числа этих слагаемых в каждых скобках:
900 ∙4+80 ∙4+5 ∙4.
Таким образом, чтобы умножить многозначное число на однозначное, достаточно умножить это однозначное число на количество единиц в каждом разряде многозначного числа, и сложить полученные результаты.
Умножение в столбик многозначного числа на однозначное
4 раза по 8 десятков – это 32 десятка. Прибавим к ним 2 десятка, которые получились после умножения однозначного числа на единицы, получим 32 десятка, то есть, 3 сотни и 2 десятка. Цифру 2 пишем под чертой в разряде десятков, а над разрядом сотен множимого 975 (в уме) ставим маленькую цифру 3 :
4 раза по 9 сотен – это 36 сотен. Прибавим к ним 3 сотни, которые держим в уме, получаем 39 сотен, или 3 тысячи и 9 сотен. Значит, пишем под горизонтальной чертой в разряде сотен цифру 9 и, поскольку в множимом 985 нет ни одной тысячи, то сразу запишем в результате под чертой цифру 3 в разряде тысяч:
Умножение многозначных чисел
Прежде чем рассказать, как в общем случае умножить одно многозначное число на другое, я расскажу о двух частных случаях умножения многозначных чисел:
Умножение на число, состоящее из единицы и любого количества нулей
327 ∙10 =3270
327 ∙100 =32700
Итак, чтобы умножить какое-нибудь число на другое, которое начинается на единицу, и заканчивается любым количеством нулей, достаточно к концу первого числа дописать столько нулей, сколько содержится во втором числе.
Умножение на число, которое начинается цифрами, и заканчивается любым количеством нулей
327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327.
(327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327).
(327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2).
(327 ∙2) ∙10.
764 ∙3 =2292.
2292 ∙100 =229200.
Итак, чтобы умножить какое-нибудь число на другое, начинающееся любыми цифрами и заканчивающееся нулями, достаточно умножить первое число на число, образованное первыми цифрами второго, а к результату приписать справа столько нулей, сколько их было в конце второго числа.
Иными словами: нужно от второго числа отбросить нули в конце, умножить получившиеся числа, а к результату приписать справа столько нулей, сколько изначально отбросили.
Общее правило умножения чисел
Количество слагаемых ( 168 ) мы можем разложить на разрядные слагаемые ( 100+60+8 ) и согласно сочетательному закону сложения сгруппировать их следующим образом : сто слагаемых плюс шестьдесят слагаемых плюс восемь слагаемых.
Исходя из определения умножения, выражения в скобках мы можем представить не в виде суммы большого количества слагаемых, а как сумму произведений:
Таким образом, чтобы умножить два многозначных числа, достаточно последовательно умножить одно из этих чисел на количество единиц каждого из разрядов второго числа, и сложить полученные результаты.
Частное произведение – это число, полученное после умножения одного из сомножителей на количество единиц какого-либо разряда другого сомножителя.
Умножение в столбик многозначных чисел
При записи действия умножения в столбик сомножители располагаются друг под другом таким образом, чтобы совпадали соответствующие разряды обоих чисел ; под множителем проводим горизонтальную черту, и ставим между сомножителями знак действия умножения:
В частных произведениях обычно не пишут (опускают) нули в конце числа для упрощения записи. При этом следует не забывать, что, первую полученную цифру частного произведения нужно писать в том разряде, цифру которого мы умножаем на множимое.
Некоторые особенности записи умножения в столбик
При записи нахождения произведения двух чисел в столбик существуют некоторые особенности, которые помогают сократить запись и упростить наглядность вычисления. Все они являются следствием свойств умножения.
Попробуйте самостоятельно доказать справедливость этого утверждения. Пишите в комментариях, получилось ли это у вас или нет.
Изменение произведения чисел при изменении его сомножителей
Если увеличить один из сомножителей в несколько раз, произведение также увеличится в это же число раз.
18 ∙2 =36
18 ∙6 =108.
По-другому и быть не может, и вот почему.
Первое произведение представляет собой сумму двух слагаемых :
18+18.
Второе произведение – это сумма шести таких же слагаемых :
18+18+18+18+18+18.
(18+18)+(18+18)+(18+18).
Если уменьшить один из сомножителей в несколько раз, произведение также уменьшится в это же число раз.
Попробуйте самостоятельно доказать правильность этого свойства. Пишите в комментариях, получилось ли это у вас?
Если увеличить один из сомножителей в несколько раз, а второй в это же число раз уменьшить, то произведение при этом не поменяется.
32 ∙8 =256,
Увеличим первый сомножитель в 4 раза, а второй во столько же раз уменьшим:
128 ∙2 =256.
Теперь уменьшим первый сомножитель произведения 32 ∙8 в 4 раза, а второй уменьшим в это же число раз:
8 ∙32 =256.
Умножение произведения на число и числа на произведение
Если необходимо умножить произведение на число, нужно любой сомножитель этого произведения умножить на данное число, а результат умножить последовательно на оставшиеся сомножители.
(a ∙b ∙c) ∙d =(a ∙d) ∙b ∙c =(b ∙d) ∙a ∙c =(c ∙d) ∙a ∙b
10 ∙7 =70 (просто приписываем к семерке нуль),
70 ∙9 =630 (находим по таблице умножения 7 ∙9 =63 и приписываем в конце нуль).
Когда я пишу «находим по таблице умножения», это означает, что мы вспоминаем эту строку из таблицы, а не ищем её там на самом деле. Таблицу умножения нужно знать наизусть!
Если необходимо умножить число на произведение, нужно умножить данное число на любой сомножитель, а результат умножить на оставшиеся сомножители.
a ∙(b ∙c ∙d) =(a ∙b) ∙c ∙d =(a ∙c) ∙b ∙d =(a ∙d) ∙b ∙c.
30 ∙3 =90,
90 ∙2 =180.
Распределительный закон умножения (умножение суммы на число)
Когда мы рассматривали умножение многозначного и однозначного чисел, мы раскладывали число 975 на его разрядные слагаемые ( 900+70+5 ), а потом умножали на 4 отдельно каждое это слагаемое. Аналогично можно поступать при умножении числа на любую сумму.
(5+2+4+9)+(5+2+4+9)+ (5+2+4+9).
Все эти слагаемые представляют собой одну сумму чисел, сгруппированных в определенные группы. Запишем их без скобок:
5+2+4+9+5+2+4+9+5+2+4+9,
а затем, используя переместительный и сочетательный законы сложения, сгруппируем одинаковые слагаемые:
Основываясь на определении действия умножение, так как мы имеем в каждых скобках одинаковые слагаемые, переписываем это выражение следующим образом:
5 ∙3+2 ∙3+4 ∙3+9 ∙3.
Распределительный закон умножения: для умножения суммы на любое число, необходимо каждое слагаемое этой суммы умножить на данное число, а затем сложить полученные произведения.
Согласно переместительному закону умножения, это свойство справедливо и при умножении числа на сумму.
Для умножения числа на сумму, необходимо умножить данное число на каждое слагаемое этой суммы, а результаты полученных произведения сложить.
(a+b+c+d)∙z =z∙(a+b+c+d) =a ∙z+b ∙z+c ∙z+d ∙z.
Название распределительный происходит от того, что действие умножения на сумму распределяется между каждым из слагаемых этой суммы.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.3 / 5. Количество оценок: 3