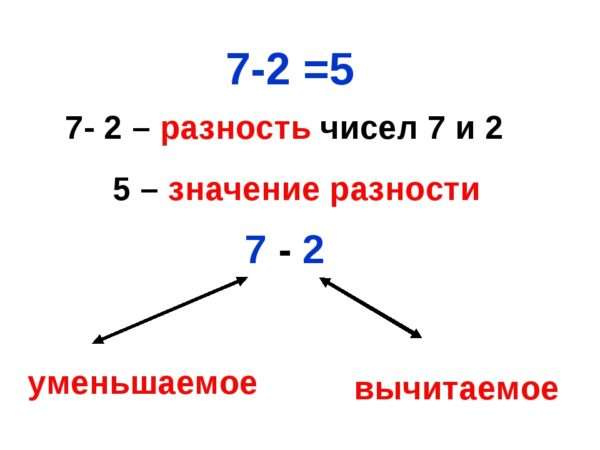
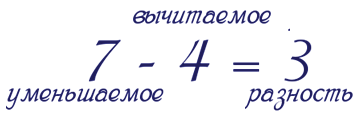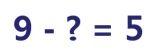Как называется уменьшаемое вычитаемое разность
Вычитание
Познакомимся с вычитанием.
Рассмотрим числовой ряд и вспомним, в каком порядке идут числа.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
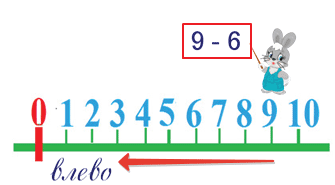
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Вычитает число 6.
Из какого числа он вычитает число 6?
Из числа 9. Мы поставили зайчика на число 9.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 6.
На каком делении он остановится? На числе 3.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
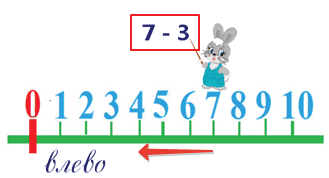
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Вычитает число 3.
Из какого числа он вычитает число 3?
Из числа 7. Мы поставили зайчика на число 7.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 3.
На каком делении он остановится? На числе 4.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
Как называются числа при вычитании?
Число, из которого вычитают, становится МЕНЬШЕ, уменьшается, поэтому его называют «уменьшаемое».
Число, которое вычитают, называют «вычитаемое».
Число, которое получается в результате вычитания, называют «разность».
У жонглёра было 9 шариков.
Когда несколько шариков упало, осталось ещё 5 шариков.
Сколько шариков упало?
Каким действием будем находить? Вычитанием.
Как называются числа при вычитании?
Как найти неизвестное вычитаемое
У жонглера было 9 шариков. Когда несколько шариков упало, осталось 5. Упали, значит, убрали.
Решаем вычитанием. Что нужно найти?
Нужно найти вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Как найти неизвестное уменьшаемое
Нужно найти уменьшаемое.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
5 + 4 = 9
Проверка вычитания
Если к разности прибавить вычитаемое, получится уменьшаемое.
Именно эта связь между разностью, уменьшаемым и вычитаемым используют для проверки вычитания.
Правильно ли произведено вычисление? Можно проверить так:
20 + 15 = 35, мы к разности прибавили вычитаемое и получили уменьшаемое. Значит, вычисление произведено верно и пример решен правильно.
Поделись с друзьями в социальных сетях:
Вычитание чисел
Вычитание чисел — это арифметическое действие, с помощью которого от единиц одного числа отнимают столько единиц, сколько их содержится в другом числе.
Пример. На столе лежало 9 конфет, 5 из них съели. Сколько конфет осталось на столе?
Чтобы ответить на этот вопрос, надо из общего количества конфет вычесть количество конфет, которые были съедены:
Отнимая 5 раз по одной конфете от общего количества конфет, мы получим количество конфет, которые остались лежать на столе, то есть 4.
Вычесть – значит от одного числа отнять столько единиц, сколько их содержится в другом.
Эта запись означает, что от 9 надо отнять пять. Справа от записи вычитания ставится знак = (равно), после которого записывается полученный результат:
Уменьшаемое, вычитаемое и разность
Уменьшаемое — это число, из которого вычитают. Вычитаемое — это число, которое вычитают. Например, в записи:
9 — это уменьшаемое, 4 — вычитаемое.
Разность (остаток) — это число, которое получается в результате вычитания. Например, в записи:
Вычитание – это арифметическое действие обратное сложению, с помощью которого по сумме и одному слагаемому находится другое слагаемое.
Проверка вычитания
где 15 — это уменьшаемое, 7 — это вычитаемое, а 8 — разность. Чтобы узнать правильно ли было выполнено вычитание, можно:
Вычитание натуральных чисел. Уменьшаемое, вычитаемое, разность.
Вычитание. Что такое уменьшаемое, вычитаемое и разность?
Понятие вычитания лучше всего рассмотреть на примере. Вы решили попить чай с конфетами. В вазе лежало 10 конфет. Вы съели 3 конфеты. Сколько конфет осталось в вазе? Если мы от 10 вычтем 3 то, в вазе останется 7 конфет. Запишем задачу математически:
Подробно разберем запись:
10 – это число от которого мы отнимаем или которое уменьшаем, поэтому его называют уменьшаемым.
3 – это число, которое мы вычитаем. Поэтому его называют вычитаемым.
7 – это число результат вычитания или еще его называют разностью. Разность показывает на сколько первое число (10) больше второго числа (3) или насколько второе число (3) меньше первого числа (10).
Если вы сомневаетесь правильно ли нашли разность, нужно сделать проверку. К разности прибавить второе число: 7+3=10
При вычитании натуральных чисел уменьшаемое не может быть меньше вычитаемого.
Делаем вывод из сказанного. Вычитание – это действие, с помощью которого по сумме и одному из слагаемых находится второе слагаемое.
В буквенном виде это выражение будет выглядеть так:
a — b = c
a – уменьшаемое,
b – вычитаемое,
c – разность.
Свойства вычитания суммы из числа.
13 — (3 + 4)=13 — 7=6
13 — 3 — 4 = 10 — 4=6
Пример можно решить двумя способами. Первый способ, найти сумму чисел (3+4), а потом вычесть от общего числа (13). Второй способ, от общего числа (13) вычесть первое слагаемое(3), а потом из полученной разности отнять второе слагаемое(4).
В буквенном виде свойство вычитания суммы из числа будет выглядеть так:
a — (b + c) = a — b — c
Свойство вычитания числа из суммы.
(7 + 3) — 2 = 10 — 2 = 8
7 + (3 — 2) = 7 + 1 = 8
(7 — 2) + 3 = 5 + 3 = 8
Чтобы вычесть из суммы число, можно это число вычесть из одного слагаемого, а потом к полученному результату разности прибавить второе слагаемое. При условии слагаемое будет больше вычитаемого числа.
В буквенном виде свойство вычитания числа из суммы будет выглядеть так:
(7 + 3) — 2 = 7 + (3 — 2)
(a + b) — c=a + (b — с), при условии b > c
(7 + 3) — 2=(7 — 2) + 3
(a + b) — c=(a — c) + b, при условии a > c
Свойство вычитания с нулем.
10 — 0 = 10
a — 0 = a
Если из числа вычесть нуль то, будет тоже самое число.
10 — 10 = 0
a — a = 0
Если из числа вычесть тоже самое число то, будет нуль.
Вопросы по теме:
В примере 35 — 22 = 13 назовите уменьшаемое, вычитаемое и разность.
Ответ: 35 – уменьшаемое, 22 – вычитаемое, 13 – разность.
Если числа одинаковые, чему равна их разность?
Ответ: нуль.
Сделайте проверку вычитания 24 — 16 = 8?
Ответ: 16 + 8 = 24
Таблица вычитания натуральных чисел от 1 до 10.

Пример №1:
Вставьте пропущенное число: а)20 — … = 20 б) 14 — … + 5 = 14
Ответ: а) 0 б) 5
Пример №2:
Можно ли выполнить вычитание: а) 0 — 3 б) 56 — 12 в) 3 — 0 г) 576 — 576 д) 8732 — 8734
Ответ: а) нет б) 56 — 12 = 44 в) 3 — 0 = 3 г) 576 — 576 = 0 д) нет
Пример №3:
Прочитайте выражение: 20 — 8
Ответ: “От двадцати отнять восемь” или “из двадцати вычесть восемь”. Правильно произносить слова
Общее представление о вычитании натуральных чисел
В рамках это материала мы разберемся с таким действием, как вычитание. Для начала мы попробуем дать общее представление о нем, пояснить сам смысл процесса вычитания. Потом введем и поясним необходимые обозначения и определения. В финальной части мы укажем, в решении каких задач нам может потребоваться вычитание.
Общий смысл процесса вычитания
Само по себе вычитание связано с разъединением некого множества на отдельные части. В этом смысле оно обратно сложению, которое, напротив, объединяет их (см. материал о сложении натуральных чисел).
Что конкретно это означает на практике?
Допустим, у нас есть некоторое количество шаров в вазе. Заберем из всей кучи один-два и положим в другое место. Тем самым мы совершили процесс вычитания, т.е. отняли от множества несколько предметов. То есть суть процесса вычитания состоит именно в исключении, отделении одних предметов от других.
Вернемся к сложению. Мы складываем одни числа с другими для того, чтобы получить сведения об их общем, суммарном количестве. А для чего мы вычитаем? Есть два подхода к пониманию сути этого процесса. От того, какой мы используем, будет зависеть смысл, придаваемый вычитаемому числу.
Для натуральных чисел результат вычитания говорит нам:
1) о том, сколько предметов останется, если убрать из их множества некое определенное количество;
2) о том, сколько нужно убрать предметов из заданного множества, чтобы получить требуемое количество.
Разберем сначала первый случай.
А во втором случае мы узнаем:
Ответ: 4
В этом смысле процесс вычитания натуральных чисел имеет смысл только тогда, когда вычитаемое число меньше, чем уменьшаемое. В самом деле, как можно убрать больше, чем у нас уже есть? В дальнейшем мы останемся в рамках этого ограничения, пока говорим о действиях с натуральными числами.
В результате вычитания у нас, разумеется, может получиться не только другое натуральное число, но и нуль, который говорит о полном отсутствии предметов. Это происходит тогда, когда уменьшаемое и вычитаемое равны. Получается, если мы уберем все предметы, которые у нас есть, то на столе не останется ни одного.
Основные понятия, связанные с вычитанием
Здесь мы укажем общепринятые обозначения и поясним их.
Выше мы уже использовали термины «уменьшаемое» и «вычитаемое». Легко понять, что они означают:
Уменьшаемое – это то, из чего вычитают, вычитаемое – то, которое вычитают.
Когда требуется определить, что получится в результате вычитания одного числа из другого, используются выражения: «вычислить разность», «найти разность», «вычесть одно число из другого», «отнять от одного числа другое».
Таким образом, весь процесс вычитания мы можем представить так: уменьшаемое минус вычитаемое равно разность.
Для решения каких задач нужно знать вычитание
С помощью вычитания можно решить широкий спектр задач. Перечислим их:
1. Найти количество предметов, которое получится после разбиения всего их множества на два других. Примером такой задачи может стать задача с шарами на столе, которую мы приводили в пункте о смысле процесса вычитания. Задачи с нахождением числа предметов, которое надо убрать из имеющегося множества, так же относятся в этому виду.
2. Решить задачи, в которых изменяются значения длины, объема, массы, времени и других измерений.
3. Узнать разницу между количеством предметов, которые входят в два разных множества, или разницу между двумя любыми величинами (скоростями, массами и др.)
Ответ: 10.
Возьмем пример с более сложными числами:
Что такое вычитаемое уменьшаемое и разность: правило
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
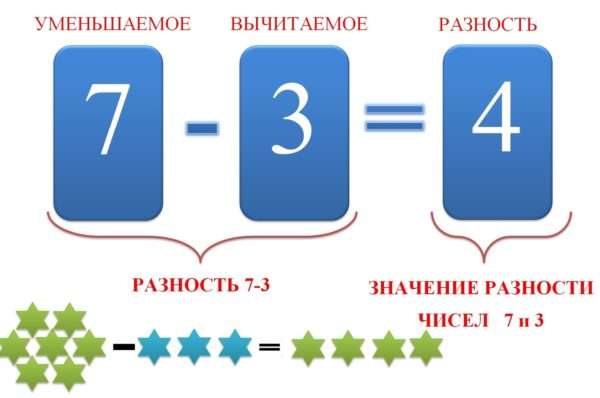
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | |
| 18 | 11 | = | 7 |
| 14 | 5 | = | 9 |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.