Как называется установление общего и различного

ОПРЕДЕЛЕНИЕ ПОНЯТИЯ

Смотреть что такое «ОПРЕДЕЛЕНИЕ ПОНЯТИЯ» в других словарях:

ОПРЕДЕЛЕНИЕ ПОНЯТИЯ “ТОКСИКОЛОГИЯ ЯДОВИТЫХ РАСТЕНИЙ”, ЕЕ ЗАДАЧИ И СВЯЗЬ С ДРУГИМИ ДИСЦИПЛИНАМИ — Токсикология ядовитых растений часть науки о ядах и их действии на человека и животных. Она дает сведения о морфологических признаках ядовитых растений, ареале их распространения, месте произрастания, условиях, при которых могут возникать… … Токсикология ядовитых растений

ОПРЕДЕЛЕНИЕ ПОНЯТИЯ “ЯДОВИТЫЕ РАСТЕНИЯ” — Ядовитыми растениями называются такие, поедание которых, иногда даже в незначительных количествах, вызывает расстройства в состоянии здоровья животных. Степень этих расстройств может быть различной; часто они сами по себе или из за развития… … Токсикология ядовитых растений

Определение понятия и группировка психопатий — Длительное время в нашей стране было распространено мнение, что психопатии являются болезненными состояниями, обусловленными биологической (наследственной или врожденной) неполноценностью нервной системы и воздействием неблагоприятных внешних… … Энциклопедический словарь по психологии и педагогике

Понятия — Понятие форма мышления, отражающая существенные свойства, связи и отношения предметов и явлений в их противоречии и развитии; мысль или система мыслей, обобщающая, выделяющая предметы некоторого класса по определённым общим и в совокупности… … Википедия

определение аксиоматическое — неявное определение понятия путем указания множества аксиом, в которые оно входит наряду с другими понятиями. Аксиома представляет собой утверждение, принимаемое без доказательства. Совокупность аксиом какой то теории является одновременно и… … Словарь терминов логики

ОПРЕДЕЛЕНИЕ — дефиниция (лат. defenitio ограничение) логическая операция, раскрывающая содержание понятия. Напр., обычное определение термометра указывает, что это, во первых, прибор и, во вторых, именно тот, с помощью которого измеряется температура. Важность … Философская энциклопедия

Определение, дедуктивный прием — Определение так назыв. дедуктивный прием, логическая операция над понятием, служащая к раскрытию его содержания; этим О. отличается от разделения понятий, служащего для раскрытия объема понятия. Определять можно только понятия; этим путем… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Определение — Определение: Определение (логика), или дефиниция логическая операция установления смысла термина. Определение (математика) введение нового понятия или объекта в математическое рассуждение путём комбинации или уточнения элементарных либо ранее… … Википедия

Определение понятий — технико юридический прием, к которому прибегает законодатель, устанавливая содержание конструируемых им правовых норм. Потребность определения используемых в законе понятий обусловлено чаще всего тем, что одно и то же понятие (термин),… … Элементарные начала общей теории права

определение классическое — (Определение через род и видовое отличие) определение, в котором предметы определяемого понятия вводятся в объем более широкого понятия и при этом с помощью отличительных признаков (видовое отличие) выделяются среди предметов этого более широкого … Словарь терминов логики

Источник

Понятие

1.Понятие как форма мышления. Содержание и объем понятия.

3.Отношения между понятиями.

4.Ограничение и обобщение понятий.

6.Деление понятий. Классификация и ее виды.

По определению, понятие – это форма мышления, отражающая предметы в их существенных признаках.При изучении этой темы с необходимостью обращаемся к общефилософским проблемам: что такое признак? какие признаки являются суще-ственными? какие – несущественными? какие признаки называются единичными? какие – общими?

Языковыми формами выражения понятий являются слова и словосочетания. Напри-мер, «книга», «человек, который смеётся», «спортсмен-перворазрядник».

Основными методами образования понятий являются: анализ – мысленное расчле-нение предметов на их составные части, свойства, признаки, синтез – мысленное со-единение в единое целое частей предмета или его признаков; сравнение – установ-

признаков объединяются в группы однородных предметов.

Всякое понятие имеет объем и содержание. Объем понятия – это совокупность (класс) предметов, мыслимых в нем, а содержание – совокупность существенных признаков, на основании которой этот класс образуется. Объем и содержание поня-тия тесно связаны между собой. Четко фиксированное содержание ведет к четкому представлению об объеме. И наоборот, неясное содержание ведет к неопределенному объему. Эта связь выражается в законе обратного отношения между объемом и содер-жанием: увеличение содержания понятия ведет к образованию понятия с меньшим объемом, и наоборот. Например, в объем понятия «студент» входят все объекты, обладающие признаком «быть учащимся вуза». Добавив в содержание понятия признак «отличник», видим, что объем понятия значительно сократился.

Виды понятий различают по двум основаниям: содержанию и объему.

По объему (количеству) различают:

1)единичные понятия, в объем которых входит только один объект (первый пре-зидент России, Организация Объединенных Наций); 2)общие понятия, в объем которых входит более одного объекта (школа, государство, озеро); 3)нулевые (пустые) понятия, в объем которых не входит ни один реально существующий объект ( баба Яга, кентавр, леший). К нулевым понятиям относятся не только фантастические порождения человеческого сознания, но и научно значимые, такие как «идеальный газ», «абсолютно твердое тело, «несжимаемая жидкость» и др.

Общие понятия могут быть регистрирующими, объем которых конечен, множество объектов, входящих в него в принципе поддается учету (планета Солнечной системы, наука, студент СПбТЭИ ) и нерегистрирующими, объем которых бесконечен (атом, существо, песчинка)

По содержанию (качеству) различают:

1)конкретные понятия, в которых мыслится самостоятельно существующий предмет (человек, здание, карандаш) и абстрактные, в которых мыслится не целый предмет, а какой-либо из признаков предмета, взятый отдельно от самого предмета (белизна, несправедливость, честность);

2)положительные понятия, в которых мыслится наличествующий у предмета

признак (алчность, отстающий ученик, грамотный человек) и отрицательные, в которых мыслится отсутствие у предмета признака (неграмотный человек, некрасивый

3)соотносительные понятия, в которых мыслятся предметы, существование одно-го из которых предполагает существование другого (родители – дети, начальник – под-чиненный, ученик – учитель) и безотносительные, в которых мыслятся предметы,

существующие самостоятельно, вне зависимости от другого предмета (дом, книга, страна);

4)собирательные понятия, в которых группа однородных предметов мыслится как единое целое (стая, созвездие, студенческая группа) и несобирательные, содержание которых можно отнести к каждому предмету данного класса (река, тетрадь, институт); собирательные понятия бывают общими (роща, полк, стадо) и единичные ( созвездие Большая Медведица).

Понятия, в содержание которых входят некоторые общие признаки, называются сравнимыми (студент и человек, черный и красный, береза и растение). Несравнимые понятия не имеют общих признаков (музыка и кирпич, беспечность и дом). Сравнимые делятся на совместимые, объемы которых частично или полностью совпадают, и несовместимые, объемы которых не совпадают ни в одном элементе.

Типы совместимости: равнообъемность (тождество), пересечение и подчинение. В отношении тождества находятся понятия, объемы которых полностью совпадают друг с другом (река Волга и самая длинная река Европы, квадрат и прямоугольный ромб). Понятия, объемы которых частично совпадают, находятся в отношении пересечения (студент и спортсмен, школьник и филателист). В отношении подчинения находятся понятия, объем одного из которых полностью входит в объем другого, но не исчерпывает его (кошка и млекопитающее, студент МГУ и студент).

Типы несовместимости: соподчинение, противоположность и противоречие.

В отношении соподчинения находятся понятия, исключающие друг друга, но при-надлежащие некоторому, более общему родовому понятию (ель, береза, липа при-надлежат объему понятия дерево) В отношении противоположности находятся два понятия, относящиеся к одному и тому же роду, одно из которых содержит какие-то

признаки, а другое эти признаки не только отрицает, но и заменяет их другими, исклю-чающими признаками (храбрость – трусость, белый – черный). Слова, выражающие противоположные понятия, являются антонимами. В отношении противоречия нахо-

дятся два понятия, которые являются видами одного и того же рода, одно из которых указывает на некоторые признаки, а другое эти признаки отрицает, не заменяя их никакими другими признаками (честный – нечестный, грамотный ученик – неграмотный ученик). Отношения между объемами понятий схематически изображаются с помощью круговых схем.

ПОНЯТИЯ

сравнимые несравнимые

совместимые несовместимые

тождество пересечение подчинение соподчинение противоположность противоречие

Операции над понятиями – наиболее сложная и важная часть учения о понятии.

Обобщить понятие – значит, перейти от понятия с меньшим объемом. но с большим содержанием, к понятию с большим объемом, но меньшим содержанием (школа – учебное заведение). Обобщение не может быть беспредельным. Пределом обобщения являются философские категории.

Ограничить понятие – значит, перейти от понятия с большим объемом к понятию с меньшим объемом посредством увеличения его содержания (геометрическая фигура – прямоугольник) Пределом ограничения является единичное понятие ( юрист – следо-ватель – следователь прокуратуры – следователь прокуратуры Выборгского района города Санкт-Петербурга И.П.Михальченко)

Логическая операция, раскрывающая содержание понятия или устанавливающая значение термина, называется определением. Если раскрывается содержание понятия, то определение называется реальным, например, «Барометр – это прибор для измерения атмосферного давления». Если определяется термин, то определение будет номинальным, например, «Слово «философия» в переводе с греческого означает «любовь к мудрости».

По способу выявления содержания понятия определения делятся на явные и неяв-ные. Явными называются определения, в которых объемы определяемого и опреде-ляющего понятия находятся в отношении равенства, эквивалентности. Самое рас-пространенное явное определение – это определение через род и видовое отличие. Сама операция определения включает в себя два этапа: 1)подведение определяемого понятия под более широкое родовое понятие и 2) указание видового отличия, то есть признака, отличающего определяемый предмет от других предметов, входящих в данный род. «Трапеция – четырехугольник, у которого две стороны параллельны, а две другие – нет». Родовым понятием в данном случае является «четырехугольник».

Правила явного определения.

1) Определение должно быть соразмерным, то есть объем определяемого понятия должен быть равен объему определяющего понятия. При нарушении этого правила возникают ошибки:

а) слишком широкое определение, когда объем определяющего понятия больше

б) слишком узкое определение, когда объем определяющего понятия меньше объема определяемого.

в) определение в одном отношении широкое, а в другом – узкое.

2) Определение не должно содержать в себе круга. Разновидностью круга в определении является тавтология.

3) определение должно быть ясным, четким, не должно содержать в себе дву-смысленностей. Ошибкой будет подмена определений метафорами, сравнениями и т.д.Встречается и такая ошибка, как определение неизвестного через неизвестное

4) определение не должно быть отрицательным.

Большинство понятий можно определить при помощи определения через род и ви-довое отличие. Но как быть с определениями категорий – предельно общих понятий, так как они не имеют рода? Не могут таким образом быть определены и единичные понятия, поскольку не имеют видового отличия. В этих случаях прибегают к неявным определениям или приемам, заменяющим определения.

К неявным определениям относятся: контекстуальное, остенсивное, аксио-матическое, определение через отношение к своей противоположности и некоторые другие. Например, понятие «категорический» может быть установлено в контексте «В своих письмах я прошу у вас только категорического, прямого ответа – да или нет»

(А.П.Чехов). Остенсивным называется определение, устанавливающее значение термина путем демонстрации предмета, обозначаемого этим термином. Можно под-вести к столу и сказать: «Это стол, и все вещи, похожие на него». Остенсивные, как и

В ряде случаев используются приемы, заменяющие определение: описание, характеристика, сравнение, разъяснение посредством примеров.

Логическая операция, раскрывающая объем понятия, называется делением. В операции деления следует различать делимое понятие – объем которого следует

раскрыть, члены деления – соподчиненные виды, на которые делится понятие (результат деления), и основание деления – признак, по которому производится деление. Сущность деления состоит в том, что предметы, входящие в объем делимого понятия, распределяются по группам.

Различают два вида деления: 1) по видообразующему признаку и 2) дихото-мическое деление. В первом случае основанием деления выступает тот признак, по которому образуются видовые понятия: «В зависимости от формы

государственного устройства государства делятся на унитарные и федеративные» Выбор основания деления зависит от цели деления и от практических задач. Но в любом случае в качестве основания должен выступать только объективный признак. Не следует, например, делить книги на интересные и неинтересные. Такое деление субъективно: одна и та же книга интересна для одного и неинтересна для другого.

Дихотомическое деление – это деление объема делимого понятия на два про-тиворечащих понятия: «Все современные государства моно разделить на демо-кратические и недемократические». Здесь не надо перечислять все виды делимого понятия: мы выделяем один вид, а затем образуем противоречащее понятие, в которое включены все другие виды. Но этот вид деления имеет недостатки. Во-первых, объем отрицательного понятия оказывается слишком широким и неопределенным. Во-вто-

рых, строгим и последовательным является по существу лишь два первых проти-воречащих понятия, а далее эта строгость и определенность может быть нарушена.

Источник

Виды понятий

Понятия принято делить на следующие виды: 1) единичные и общие, 2) собирательные и несобирательные, 3) конкретные и аб­страктные, 4) положительные и отрицательные, 5) безотноситель­ные и соотносительные.

1. Понятия делятся на единичные и общие в зависимости от того, мыслится в них один элемент или множество элементов. Понятие, в котором мыслится один элемент, называется единичным (например, «Москва», «Л.Н. Толстой», «Российская Федерация»). Понятие, в котором мыслится множество элементов, называется общим (напри­мер, «столица», «писатель», «федерация»).

Общие понятия могут быть регистрирующими и нерегистрирую­щими. Регистрирующими называются понятия, в которых множест­во мыслимых в нем элементов поддается учету, регистрируется (во всяком случае в принципе). Например, «участник Великой Отечест­венной войны 1941—1945 гг.», «родственники потерпевшего Шило­ва», «планета Солнечной системы». Регистрирующие понятия имеют конечный объем. Общее понятие, относящееся к неопределенному числу элемен­тов, называется нерегистрирующим. Так, в понятиях «человек», «следователь», «указ» множество мыслимых в них элементов не под­дается учету: в них мыслятся все люди, следователи, указы прошед­шего, настоящего и будущего. Нерегистрирующие понятия имеют бесконечный объем.

2. Понятия делятся на собирательные и несобирательные. Поня­тия, в которых мыслятся признаки некоторой совокупности элемен­тов, составляющих единое целое, называются собирательными. На­пример, «коллектив», «полк», «созвездие». Эти понятия отражают множество элементов (членов коллектива, солдат и командиров полка, звезд), однако это множество мыслится как единое целое. Содержание собирательного понятия нельзя отнести к каждому отдельному элементу, входящему в его объем, оно относится ко всей совокупности элементов. Например, существенные признаки кол­лектива (группа лиц, объединенных общей работой, общими интере­сами) неприложимы к каждому отдельному члену коллектива. Соби­рательные понятия могут быть общими («коллектив», «полк», «созвездие») и единичными («коллектив нашего института», «86-й стрелковый полк», «созвездие Большой Медведицы»).

Понятие, в котором мыслятся признаки, относящиеся к каждому его элементу, называется несобирательным. Таковы, например, по­нятия «звезда», «командир полка», «государство».

В процессе рассуждения общие понятия могут употребляться в разделительном и собирательном смысле. Если высказывание относится к каждому элементу класса, то такое употребление понятия будет разделительным; если же вы­сказывание относится ко всем элементам, взятым в единстве, и неприложимо к каждому элементу в отдельности, то такое употребление понятия называется собирательным. Например, выска­зывая мысль «Студенты 1-го курса изучают логику», мы употреб­ляем понятие «студенты 1-го курса» в разделительном смысле, так как данное утверждение относится к каждому студенту 1-го курса. В высказывании «Студенты 1-го курса провели теоретическую кон­ференцию» утверждение относится ко всем студентам 1-го курса в целом. Здесь понятие «студенты 1-го курса» употребляется в собирательном смысле. Слово «каждый» к данному суждению не­приложимо.

3. Понятия делятся на конкретные и абстрактные в зависимости от того, что они отражают: предмет (класс предметов) или его при­знак (отношение между предметами). Понятие, в котором мыслится предмет или совокупность предметов как нечто самостоятельно существующее, называется конкрет­ным; понятие, в котором мыслится признак предмета или отноше­ние между предметами, называется абстрактным. Так, понятия «книга», «свидетель», «государство» являются конкретными; поня­тия «белизна», «смелость», «ответственность» — абстрактными. Различие между конкретными и абстрактными понятиями осно­вано на различии между предметом, который мыслится как целое, и свойством предмета, отвлеченным от последнего и отдельно от него не существующим. Абстрактные понятия образуются в результате отвлечения, абстрагирования определенного признака предмета; эти признаки мыслятся как самостоятельные объекты мысли. Так, понятия «смелость», «инвалидность», «невменяемость» отражают признаки, не существующие сами по себе, в отрыве от лиц, обладаю­щих этими признаками. Понятия «дружба», «посредничество», «психологическая несовместимость» отражают определенные отно­шения. Это абстрактные понятия.

Не следует смешивать конкретные понятия с единичными, а аб­страктные с общими. Общие понятия могут быть и конкретными, и абстрактными (например, понятие «посредник» — общее, конкрет­ное; понятие «посредничество» — общее, абстрактное). Как кон­кретным, так и абстрактным может быть единичное понятие (напри­мер, понятие «Организация Объединенных Наций» — единичное, конкретное; понятие «мужество капитана Гастелло» — единичное, абстрактное).

4. Понятия делятся на положительные и отрицательные в зависи­мости от того, составляют ли их содержание свойства, присущие предмету, или свойства, отсутствующие у него. Понятия, содержание которых составляют свойства, присущие предмету, называются положительными. Понятия, в содержании которых указывается на отсутствие у предмета определенных свойств, называются отрицательными. Так, понятия «грамотный», «порядок», «верующий» являются положительными; понятия «не­грамотный», «беспорядок», «неверующий» — отрицательными. В русском языке отрицательные понятия выражаются обычно словами с отрицательными приставками «не» и «без»: «неулови­мый», «невиновный», «бездействие»; в словах иностранного проис­хождения — чаще всего словами с отрицательной приставкой «а»: «аморальный», «анонимный», «асимметрия» и т.д. Однако на отсут­ствие некоторых свойств предмета могут указывать слова без отрицательной приставки. Например: «темнота» (отсутствие света), «трезвый» (непьяный), «молчаливый» (неразговорчивый). С другой стороны, понятия «безделушка» (вещица для украшения), «невин­ный» (чистосердечный, простодушный), «негодование» (возмуще­ние, крайнее недовольство) относятся к положительным; они не содержат отрицания каких-либо свойств, хотя выражающие их слова могут быть ошибочно восприняты как слова с отрицательными при­ставками.

5. Понятия делятся на безотносительные и соотносительные в зависимости от того, мыслятся ли в них предметы, существующие раздельно или в отношении с другими предметами. Понятия, отражающие предметы, существующие раздельно и мыслящиеся вне их отношения к другим предметам, называются безотносительными. Таковы понятия «студент», «государство», «место преступления» и др. Соотносительные понятия содержат признаки, указывающие на отношение одного понятия к другому понятию. Например: «родители» (по отношению к понятию «дети») или «дети» (по отношению к понятию «родители»), «начальник» («подчиненный»), «получение взятки» («дача взятки»). Соотноси­тельными являются также понятия «часть», «причина», «брат», «сосед» и др. В этих понятиях отражены предметы, существование одного из которых не мыслится вне его отношения к другому.

Определить, к какому виду относится то или иное понятие, — значит дать ему логическую характеристику. Так, давая логическую характеристику понятию «Российская Федерация», нужно указать, что это понятие единичное, собирательное, конкретное, положи­тельное, безотносительное. При характеристике понятия «невменя­емость» должно быть указано, что оно является общим (нерегистри­рующим), несобирательным, абстрактным, отрицательным, безотно­сительным.

Логическая характеристика понятий помогает уточнить их содер­жание и объем, вырабатывает навыки более точного употребления понятий в процессе рассуждения.

§ 4. Отношения между понятиями

Рассматривая отношения между понятиями, следует всего различать понятия сравнимые и несравнимые.

Сравнимыми называются понятия, имеющие некоторые призна­ки, позволяющие эти понятия сравнивать друг с другом. Например, «пресса» и «телевидение» — сравнимые понятия, они имеют общие признаки, характеризующие средства массовой информации.

Несравнимыми называются понятия, не имеющие общих при­знаков, поэтому и сравнивать эти понятия невозможно. Например: «квадрат» и «общественное порицание», «преступление» и «косми­ческое пространство», «государство» и «симфоническая музыка» Они относятся к разным, весьма отдаленным друг от друга областям действительности и не имеют признаков, на основании которых их можно было бы сравнивать друг с другом. В логических отношениях могут находиться только сравнимые понятия.

Сравнимые понятия делятся на совместимые и несовместимые.

Понятия, объемы которых полностью или частично совпадают, называются совместимыми. В содержании этих понятий нет при­знаков, исключающих совпадение их объемов. Существуют три вида отношений совместимости:

1) равнообьемность, 2) пересечение (перекрещивание) и 3) подчинение (субординация).

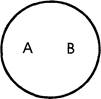
1. В отношении равнообъемности находятся понятия, в которых мыслится один и тот же предмет. Объемы этих понятий полностью совпадают (хотя содержание различно). В отношении равнообъем­ности находятся, например, понятия «геометрическая фигура с тремя равными углами» и «геометрическая фигура с тремя равными сторонами». Эти понятия отражают один предмет мысли: равно­угольный (равносторонний) треугольник, их объемы полностью со­впадают, однако содержание различно, поскольку каждое из них содержит разные признаки треугольника.

Отношение между понятиями принято изображать с помощью круговых схем (кругов Эйлера), где каждый круг обозначает объем понятия, а каждая его точка — предмет, мыслимый в его объеме. Круговые схемы позволяют наглядно представить отношение между различными понятиями, лучше понять и усвоить эти отношения.

Так, отношение между двумя равнообъемными понятиями долж­но быть изображено в виде двух полностью совпадающих кругов А и В (рис. 1).

В совместившейся части кругов А и В (заштрихованная часть схемы) мыслятся те юристы, которые являются преподавателями, а в несовместившейся части круга А — юристы, не являющиеся пре­подавателями, в несовместившейся части круга В — преподаватели, не являющиеся юристами.

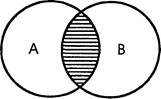
2. В отношении пересечения (перекрещивания) находятся поня­тия, объем одного из которых частично входит в объем другого. Содержание этих понятий различно.

В отношении пересечения находятся понятия «юрист» (А) и «преподаватель» (В): некоторые юристы являются преподавателя­ми (как некоторые преподаватели — юристами). С помощью круго­вых схем это отношение изображается в виде двух пересекающихся кругов (рис. 2).

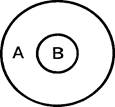
3. В отношении подчинения (субординации) находятся понятия, объем одного из которых полностью входит в объем другого, состав­ляя его часть.

В таком отношении находятся, например, понятия «суд» (А) и «городской суд» (В). Объем первого понятия шире объема второго понятия, кроме городских существуют и другие виды судов — крае­вые, областные, районные и т.д. Понятие «городской суд» полнос­тью входит в объем понятия «суд» (рис. 3).

Понятие, имеющее больший объем и включающее объем другого понятия, называется подчиняющим (А), понятие, имеющее мень­ший объем и составляющее часть объема другого понятия, — подчи­ненным (В).Если в отношении подчинения находятся два общих понятия, то подчиняющее понятие называется родом, подчиненное — видом. Так, понятие «городской суд» будет видом по отношению к понятию «суд». Понятие может быть одновременно видом (по отношению к более общему понятию) и родом (по отношению к понятию менее общему). Например: понятие «лишение свободы на определенный срок» (В) — это род по отношению к понятию «лишение свободы на пять лет» (С) и в то же время вид по отношению к понятию «уголов­ное наказание» (А). Отношение между тремя подчиненными друг другу понятиями изображено на рис. 4.

Если в отношении подчинения находятся общее и единичное (индивидуальное) понятия, то общее (подчиняющее) понятие яв­ляется видом, а единичное (подчиненное) индивидом. В таком от­ношении будут находится, например, понятия «адвокат» и «Ф.Н. Плевако». Отношения «род» — «вид» — «индивид» широко используются в логических операциях с понятиями — в обобщении, ограничении, определении и делении.

Понятия, объемы которых не совпадают ни полностью, ни час­тично, называются несовместимыми (или внеположными). Эти понятия содержат признаки, исключающие совпадение их объ­емов.

Существуют три вида отношений несовместимости: 1) соподчине­ние (координация), 2) противоположность (контрарность), 3) про­тиворечие (контрадикторность).

1. В отношении соподчинения (координации) находятся два или больше неперекрещивающихся понятий, подчиненных общему для них понятию. Например: «областной суд» (В), «городской суд» (С), «суд» (А). Понятия, находящиеся в отношении подчинения к обще­му для них понятию, называются соподчиненными.

В круговых схемах это отношение изображено на рис. 5.

2. В отношении противоположности (контрарности) находятся понятия, одно из которых содержит некоторые признаки, а дру­гое — признаки, не совместимые с ними. Такие понятия называются противоположными (контрарными). Объемы двух противополож­ных понятий составляют в своей сумме лишь часть объема общего для них родового понятия, видами которого они являются и которо­му они соподчинены; Таковы, например, отношения между поня­тиями «черный» и «белый», «отличник» и «неуспевающий», «друже­ственное государство» и «враждебное государство» (рис. 6). Пункти­ром изображено родовое понятие «государство», так как оно не дано, но может быть образовано.

Понятие В содержит признаки, не совместимые с признаками понятия А. Объемы этих понятий не исчерпывают в своей сумме всего объема родового понятия «государство»: существуют и другие межгосударственные отношения.

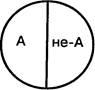
3. В отношении противоречия (контрадикторности) находятся понятия, одно из которых содержит некоторые признаки, а другое эти же признаки исключает.

Объемы двух противоречащих понятий составляют весь объем рода, видами которого они являются и которому они соподчи­нены.

В отношении противоречия находятся положительные и отрица­тельные понятия: «четный» и «нечетный», «успевающий» и «неуспе­вающий»,

«дружественное государство» и «недружественное госу­дарство».

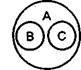Из схемы видно, что положительное понятие А и отрицательное понятие не-А исчерпывают весь объем понятия «государство»: любое государство является дружественным или недружественным. Между двумя противоречащими понятиями не может быть никакого третьего понятия.

Источник