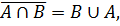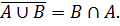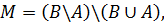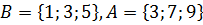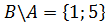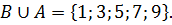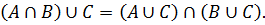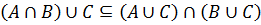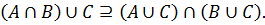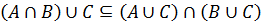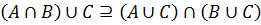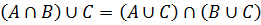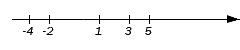Как называется знак пересечения множеств
Математика часто оперирует абстрактными объектами, для задания связи между которыми существуют различные операции, такие как пересечение и объединение множеств. Понятие множества является интуитивным, не определяемым. Оно обычно ассоциируется с набором чего-либо, группой каких-то предметов или живых объектов, совокупностью некоторых условий, рассматривается как класс, семейство в некоторой классификации, промежуток числовой прямой. Например, в геометрии рассматриваются линии как множества точек.
То, из чего состоит множество, называется его элементами.
Графическим изображением, служащим для наглядности рассматриваемых объектов, является круг Эйлера.
Что такое пересечение множеств
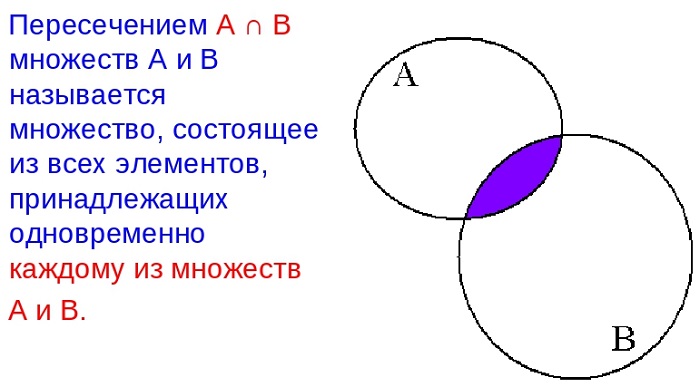
Для любого набора множеств их пересечением называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из заданных. Другими словами, это совокупность всех общих элементов.
С помощью кругов Эйлера-Венна пересечение можно изобразить так:
Часто применяется для определения решений систем уравнений и неравенств.
Ассоциируется с обычным умножением двух числовых объектов.
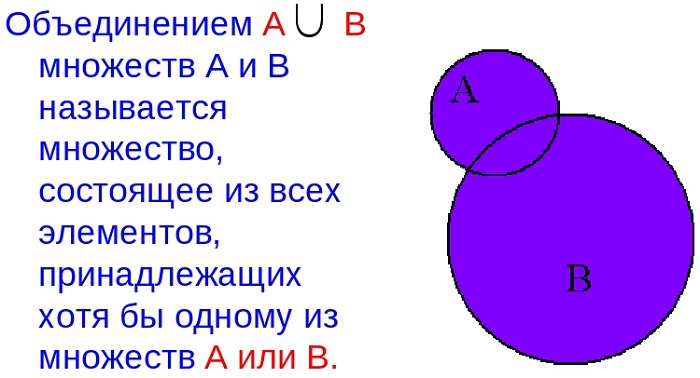
Что такое объединение множеств
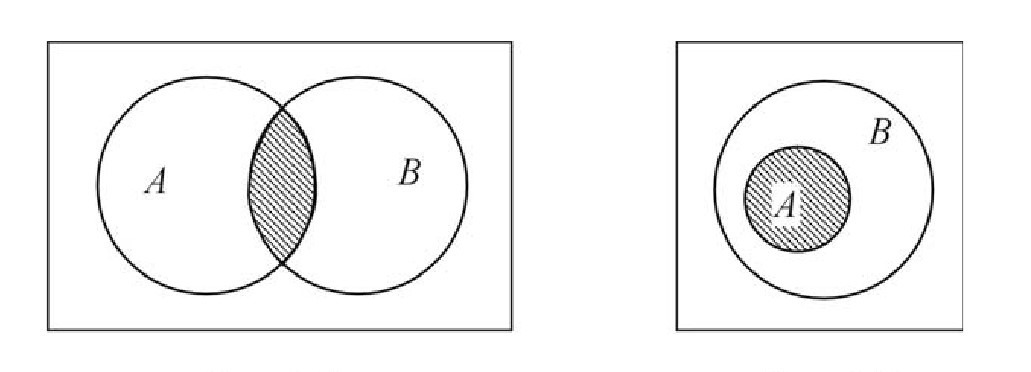
Изображение кругами Эйлера выглядит следующим образом:
Часто используется при решении уравнений и неравенств, подчёркивая наличие серий корней и решений, нескольких используемых промежутков числовой прямой.
В обычной математике близко по смыслу с операцией, называемой «сложение».
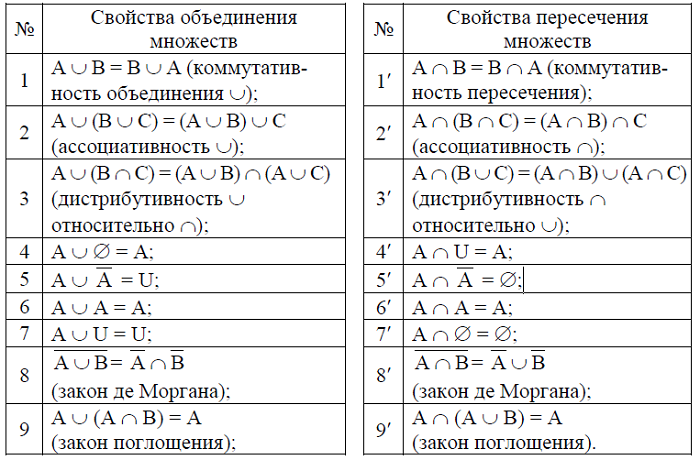
Свойства пересечения и объединения множеств
Для решения задач нужно знать о следующих свойствах:
1. Коммутативность (перестановочность):
Эти свойства распространяются на любое количество компонентов. Следуют из определения операций.
2. Ассоциативность (расстановка скобок):
Данные свойства также применимы к большому количеству компонентов. Позволяют опускать скобки и упрощать запись.
3. Дистрибутивность (раскрытие скобок):
(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C);
(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C).
4. Закон идемпотентности (идентичности):
Множество, не содержащее ни одного элемента, называется пустым. Обозначается перечёркнутым нулём: Ø
Выполнение операций с Ø:
Прослеживается аналог со сложением и умножением на ноль.
Операции над множествами
Помимо объединения и пересечения существуют другие операции:
Для двух множеств A и B можно определить их разность как набор элементов, входящих в A и не содержащихся в B:
Рассматривая некоторое множество в качестве содержащего все остальные, можно прийти к понятию «дополнение», как к совокупности всех элементов, не входящих в A:
Благодаря этой операции свойства объединения и пересечения можно расширить/
Примеры решения задач
Задача №1
Выписать все элементы множества
При поиске M операции выполняются последовательно.
B \ A состоит из всех элементов B, которые не принадлежат A, поэтому:
B ∪ A включает в себя все элементы, принадлежащие хотя бы одному из множеств A или B. Таким образом:
M = (B \ A) \ (B ∪ A) состоит из всех элементов B \ A, которые не принадлежат B ∪ A, следовательно, M = Ø.
Задача №2
Доказать методом включений тождество:
Необходимо доказать выполнение включений:
Выбирается произвольный x из (A ∩ B) ∪ C. По определению операции объединения x ∈ B ∩ A или x ∈ C.
Если x ∈ B ∩ A, то по определению пересечения x ∈ B и x ∈ A.
Так как x ∈ A, то x ∈ C ∪ A; так как x ∈ B, то x ∈ C ∪ B, следовательно, x ∈ (A ∪ C) ∩ (B ∪ C).
Если x ∈ C, то x ∈ C ∪ A и x ∈ C ∪ B, а значит: x ∈ (A ∪ C) ∩ (B ∪ C).
Поскольку x ∈ (A ∩ B) ∪ C был выбран произвольно, утверждается, что любой элемент этого множества содержится в (A ∪ C) ∩ (B ∪ C), то есть:
Выбирается произвольный y из (A ∪ C) ∩ (B ∪ C).
По определению операции пересечения y ∈ C ∪ A и y ∈ C ∪ B.
Так как y ∈ C ∪ A, то y ∈ A или y ∈ C; так как y ∈ C ∪ B, то y ∈ C или y ∈ B. Таким образом, y ∈ C или y ∈ A и y ∈ B.
Если y ∈ A и y ∈ B, то y ∈ B ∩ A, а, следовательно, y ∈ (A ∩ B) ∪ C; если y ∈ C, то также y ∈ (A ∩ B) ∪ C.
Поскольку y из (A ∪ C) ∩ (B ∪ C) выбирался произвольно, утверждается, что любой элемент этого множества содержится в (A ∩ B) ∪ C, то есть
Из пунктов 1 и 2 вытекает, что
Пересечение и объединение множеств
Вы будете перенаправлены на Автор24
В результате математических операций над множествами из исходных множеств получается новое множество, причем этот результат однозначен. Примерами таких операций являются пересечение и объединение множеств. Эти операции производятся по определенным правилам, о которых пойдет речь ниже.
Объединение двух множеств представляет собой совокупность таких элементов, что каждый из них является элементом одного из исходных множеств. Пересечение же множеств состоит из всех элементов, общих для исходных множеств.
Обозначения множеств. Знаки объединения и пересечения множеств
В такой форме объединение записывается как
Для графического выражения операций пересечения и объединения применяются знаки пересечения и объединения множеств:
Готовые работы на аналогичную тему
Правила нахождения пересечений и объединений
Правила для нахождения пересечений и объединений множеств заключаются в следующем:
Для нахождения пересечения нескольких конечных множеств, нужно перебрать числа первого из них и выяснить, принадлежит ли текущий элемент каждому из рассматриваемых множеств. Если это условие не соблюдается, он не принадлежит пересечению. В качестве проверочного (элементы которого перебираются) следует выбирать множество с наименьшим числом элементов.
$A \cap B \cap C \cap D = \<1, 2\>$.
Исследование множеств с помощью координатной прямой
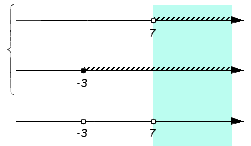
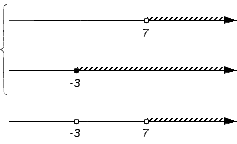
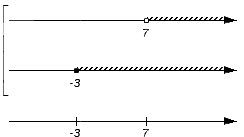
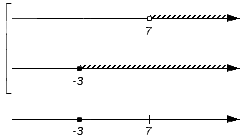
С помощью координатной прямой удобно анализировать пересечения и объединения множеств. Они изображаются друг под другом на координатных прямых с совпадающими точками и направлениями отсчета. Для отображения объединения множеств координатные прямые отмечают слева квадратной скобкой, для обозначения пересечения используется фигурная скобка.
Для решения применим графический метод:
Рисунок 1. Графическое решение задачи. Автор24 — интернет-биржа студенческих работ
Ответ:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 05 03 2021
Объединение множеств
Что такое объединение и пересечение множеств А и Б
Множество — это совокупность объединенных по какому-либо признаку объектов любой природы.
Оно может состоять из чисел, букв, прямых, точек, слов и т.д. Эти объекты, которые совокупно образуют данное множество, являются его элементами или точками.
Для обозначения множеств применяют заглавные буквы латинского алфавита. А их элементы обозначают строчными буквами. Например, запись \( x\in K\) означает, что х является элементом множества \(К.\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Множество называется подмножеством, когда оно возникает не как самостоятельный объект, а когда оно является частью другого множества, и все его элементы также являются элементами другого множества. Записывается как \(А\;\subset\;Б.\)
Если множества А и Б содержат одинаковые элементы, то они равны:
Если множество не содержит в себе ни одного элемента, то оно называется пустым и является подмножеством любого множества. Оно обозначается символом \(Ø.\)
Если пустое множество пересекается с другим, то их общее множество будет так же пустым:
Если множества равны, то всякий элемент х, принадлежащий правой части равенства, принадлежит и левой, и наоборот.
Основные операции с множествами подразделяются на:
Понятие и свойства объединения множеств
Множество С называют объединением (или суммой) множеств А и Б, если его элементы принадлежат хотя бы одному из указанных множеств. То есть в множестве С содержатся элементы как А, так и Б, и любое множество, которое будет обладать этим свойством, будет содержать С.
Объединение С множеств А и Б обозначается таким образом:
Пусть имеется два множества:
Тогда их объединением будет служить множество С = <2; 3; 4; 6; 8; 9>.
Свойства объединений:
Некоторые свойства операции объединений напоминают по своему принципу привычную операцию «сложения» чисел. При этом некоторые свойства объединения, которые соответствуют определенным операциям сложения чисел, будут иметь свои особенности.
Свойства объединения, которые справедливы для любых множеств A, Б и C:
A U Б = Б U A; A U (Б U C) = (A U Б) U C.
\(А\subset А\cup Б\;и\;Б\subset А\cup Б.\)
Кроме того, из включения \(А\subset Б\) следует включение:
\(А\cup С\subset Б\cup С.\)
В частности, любому множеству A соответствует равенство:
Это равенство означает идемпотентность объединения, то есть повторное осуществление операции по отношению к объекту будет давать тот же результат, что и в первый раз.
Если у множеств А и Б есть общие элементы, то каждый из этих элементов не повторяется в объединении, и входят в него один раз.
Понятие и свойства пересечения множеств
Пересечением множеств А и Б является множество С, включающее в себя элементы, принадлежащие одновременно и А, и Б, то есть элементов, общих для этих множеств.
Пресечение множеств обозначают символом \(∩\) :
Пусть имеется два множества:
A = <2; 3; 6; 8>и Б = <4; 6; 8; 9>; тогда их пересечением будет являться C = <6; 8>.
Свойства пересечений:
Некоторые свойства операции пересечений напоминают по своему принципу привычную операцию «умножения» чисел. При этом некоторые свойства пересечения, которые соответствуют определенным операциям умножения чисел, будут иметь свои особенности.
Свойства пересечения, которые справедливы для любых множеств A, B и C:
A ∩ Б = Б ∩ A; A ∩ (Б ∩ C) = (A ∩ Б) ∩ C.
\(А\cap Б\subset А\;и\;А\cap Б\subset Б.\)
Если у множеств А и Б нет общих элементов, то их пересечением является пустое множество, иначе говорят, что они не пересекаются.
Кроме того, из включения \(А\subset Б\) следует включение:
\(А\cap С\subset Б\cap С.\)
В частности, для любого множества A имеет место равенство \( А\cap\varnothing=\varnothing.\)
Также верно равенство \(А\cap А=А.\)
Здесь, как и в объединении, встречается свойство идемпотентности пересечения. Поэтому здесь не говорят о возведении множества в степени в том привычном смысле, какое применимо к степени числа. Этим операция пересечения отличается от операции умножения чисел, что легко доказывается на различных множествах.
\(C=\underset<\alpha\in I>\cup A_\alpha=\underset\alpha\cup A_\alpha;\)
в случае пересечения:
Правила нахождения пересечений и объединений, формулы
Конечное множестве А обладает мощностью, представляющей собой число элементов. Его обозначают как \(|А|\) или #А.
Если известны мощности каждого множества и их пересечений, то по следующей формуле можно найти мощность объединения:
\(\left|А\cup Б\right|=\left|А\right|+\left|Б\right|-\left|А\cap Б\right|;\)
\(\left|А\cup Б\cup С\right|=\left|А\right|+\left|Б\right|+\left|С\right|-\left|А\cap Б\right|-\left|А\cap С\right|-\left|Б\cap С\right|+\left|А\cap Б\cap С\right|.\)
Вообще \(\left|А_1\cup. \cup А_n\right|\) равно
Она называется формулой включений и исключений.
В частности, произведение характеристических функций соответствует пересечению множеств:
Если Х является характеристической функцией исходного множества, то дополнению (до К) соответствует функция 1 — Х.
Запишем в виде суммы значений характеристической функции число элементов множества:
Объединение \(A_1\cup. \cup A_n\) представим в виде дополнения к пересечению дополнений множеств \(A_i.\)
Опираясь на термины характеристических функций, получим:
Раскроем скобки в правой части:
Получим формулу включений и исключений, просуммировав правую и левую части по всем элементам К. которые являются функциями на К.
Исследование множеств с помощью координатной прямой
Координатная прямая — прямая линия, содержащая начало отсчета, единичный отрезок и направление.
Для любого натурального числа на координатной прямой можно выбрать соответствующую только ему единственную точку. Каждому числу на данной прямой можно подобрать противоположное число, которое расположено симметрично относительно начала отсчета и отличается от другого только знаком.
Также каждому действительному (рациональному или иррациональному) на координатной прямой соответствует единственная точка и, наоборот, для каждой ее точки есть единственное действительное число. Это называется взаимно однозначным соответствием. С учетом этого соответствия,множество R действительных чисел и множество точек координатной прямой часто объединяют общим термином — «числовая прямая».
Ось Оу образована множеством точек х = 0, поэтому ось Оу является графиком уравнения х — 0.
Ось Ох образована множеством точек у = 0, поэтому ось Ох является графиком уравнения у — 0.
Множество точек у = х образует прямую, которая проходит через начало координат и делит I и III квадранты пополам.
В математике есть важное понятие упорядоченной пары (х, у), которое представлено либо элементами одного и того же множества, либо элементами разных множеств Х и У.
Свойством упорядоченных пар является то, что две упорядоченные пары ( \(x_1, y_1)\) и \( (x_2)\) и \((y_2)\) будут называться равными, когда \( x_1=x_2\ и\ y_1=y_2.\)
Первой компонентой (координатой) пары (х, у) является элемент х, второй компонентой (координатой) той же пары — элемент у.
Понятие упорядоченной пары поваляет ввести дополнительную операцию над множествами — прямое или декартово умножение, имеющее вид:
Для определения упорядоченного набора n+1 элементов применяется метод математической индукции:
Отсюда выводится произведение множеств:
\(X_1\times X_2\times. X_
Чтобы установить между точками координатной прямой соответствие и между множеством натуральных чисел, на прямой выбирают произвольную точку 0, а затем с помощью единичного отрезка отмечают на ней точки, которым соответствуют натуральные числа.
Соответственно, чем правее число расположено на координатной прямой, тем оно больше.
Отсюда следует:
Как определить пересечение и объединение при помощи изображений числовых множеств
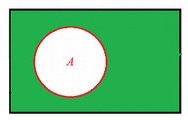
Взаимоотношения и операции между множествами можно наглядно проиллюстрировать, применяя диаграммы Эйлера-Венна. Множества в этих диаграммах чаще всего изображаются в виде кругов и их внутренностями, а в виде прямоугольника изображено универсальное множество U.
В диаграммах Эйлера-Венна имеет значение взаимное расположение, а не их относительный размер.
Изображение пересечения
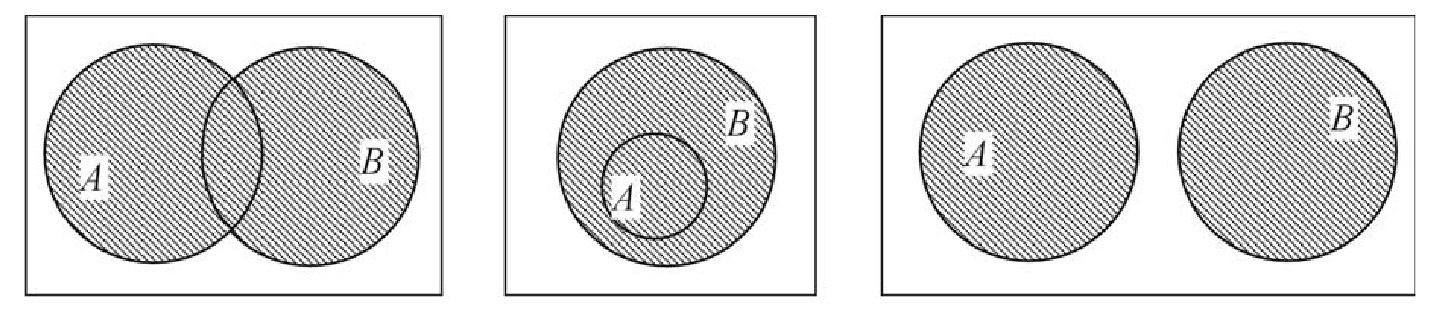
Изображение объединения
Рисунок демонстрирует, что если A подмножество множества B, т.е.
\(A\subset B,\;то\;A\cup B=B, \)
то раз включать элементы множества А в объединение не требуется, поскольку его элементы принадлежат и множеству B.
Основные законы операций объединения и пересечения множеств
Закон коммутативности
\(A\cup B=B\cup A,\;A\cap B=B\cap A.\)
Коммутативный закон показывает, что изменение порядка множеств в указанных операциях не влияет на их итог. Действительно, множества \(A\cup B\;и\;B\cup A\;\) состоят из элементов, которые относятся хотя бы к одному из множеств A или B, и не содержат никаких других элементов. А множества \(A\cap B\;и\;B\cap A\) включают в себя все элементы, относящиеся к каждому из множеств A и B.
Закон ассоциативности
\(A\cup(B\cup C)=(A\cup B)\cup C,\;A\cap(B\cap C)=(A\cap B)\cap C.\)
Ассоциативность указанных операций позволяет опускать фиксацию посредством скобок порядка проведения операций. Действительно, множества \(A\cup(B\cup C)\;и\;(A\cup B)\cup C\) состоят из всех элементов, входящих хотя бы в одно из множеств A, B и C и не содержат никаких других элементов, а множества \(A\cap(B\cap C)\;и\;(A\cap B)\cap C\) состоят только из общих элементов множеств A, B и C. Заметим, что по закону ассоциативности конечный результат не зависит от порядка действий. Но промежуточные результаты — зависят.
Закон дистрибутивности
\(A\cup(B\cap C)=(A\cup B)\cap(A\cup C),\;A\cap(B\cup C)=(A\cap B)\cup(A\cap C).\)
В числовом случае дистрибутивность умножения относительно сложения позволяет осуществлять вынос общего множителя за скобку и проводить раскрытие скобок. В случае множеств это так же справедливо, при этом соотношений такого рода больше.
Нахождение пересечения и объединения числовых множеств, что такое пересечение множеств
Решение некоторых математических задач предполагает нахождение пересечения и объединения числовых множеств. В статье ниже рассмотрим эти действия подробно, в том числе, на конкретных примерах. Полученный навык будет применим для решения неравенств с одной переменной и систем неравенств.
Простейшие случаи
Когда мы говорим о простейших случаях в рассматриваемой теме, то имеем в виду нахождение пересечения и объединения числовых множеств, представляющих из себя набор отдельных чисел. В подобных случаях будет достаточно использования определения пересечения и объединения множеств.
Объединение двух множеств – это множество, в котором каждый элемент является элементом одного из исходных множеств.
Пересечение множеств – это множество, которое состоит из всех общих элементов исходных множеств.
Из указанных определений логически следуют следующие правила:
— чтобы составить объединение двух числовых множеств, имеющих конечное количество элементов, необходимо записать все элементы одного множества и дописать к ним недостающие элементы из второго множества;
— чтобы составить пересечение двух числовых множеств, необходимо элементы первого множества один за другим проверить на принадлежность второму множеству. Те из них, которые окажутся принадлежащими обоим множествам и будут составлять пересечение.
Полученное согласно первому правилу множество будет включать в себя все элементы, принадлежащие хотя бы одному из исходных множеств, т.е. станет объединением этих множеств по определению.
Множество, полученное согласно второму правилу, будет включать в себя все общие элементы исходных множеств, т.е. станет пересечением исходных множеств.
Рассмотрим применение полученных правил на практических примерах.
Решение
Однако на практике, чтобы найти объединение и пересечение трех и более простейших числовых множеств, которые состоят из конечного количества отдельных чисел, удобнее применять правила, аналогичные указанным выше.
Что же касается решения задачи на нахождение пересечения трех и более числовых множеств, которые состоят из конечного количества отдельных чисел, необходимо одно за другим перебрать числа первого множества и поэтапно проверять, принадлежит ли рассматриваемое число каждому из оставшихся множеств. Для пояснения рассмотрим числовые множества:
Координатная прямая и числовые промежутки как объединение их частей
Как определить пересечение и объединение при помощи изображений числовых множеств
С темой нахождения пересечения и объединения множеств возможно наглядно разобраться, если использовать изображения заданных множеств на координатной прямой (если только речь – не о простейших случаях, рассмотренных в самом начале статьи).
Мы рассмотрим общий подход, который позволяет определить результат пересечения и объединения двух числовых множеств. Опишем подход в виде алгоритма. Рассматривать его шаги будем постепенно, каждый раз приводя очередной этап решения конкретного примера.
Решение
В нашем примере для записи пересечения и объединения числовых множеств имеем: 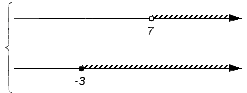
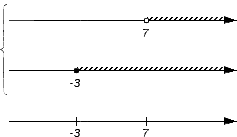
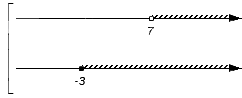
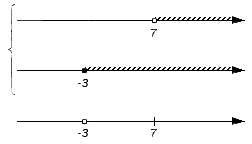
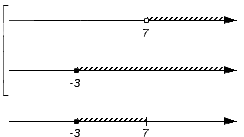
Теперь необходимо поочередно проверить принадлежность каждого из записанных множеств искомому пересечению или объединению. Получаемые выводы поэтапно отмечаются на нижней координатной прямой: когда промежуток является частью пересечения или объединения, над ним рисуется штриховка. Когда точка входит в пересечение или объединение, то штрих заменяется на сплошную точку; если точка не является частью пересечения или объединения – ее делают выколотой. В этих действиях нужно придерживаться таких правил:
-. промежуток становится частью пересечения, если он одновременно является частью множества A и множества B (или иными словами – если есть штриховка над этим промежутком на обеих координатных прямых, отображающих множества А и B );
— точка становится частью пересечения, если она является одновременно частью каждого из множеств А и В (иными словами – если точка является невыколотой или внутренней точкой какого-либо интервала обоих числовых множеств A и B );
— точка становится частью объединения, если она является частью хотя бы одного из множеств A и B (иными словами – точка является невыколотой или внутренней точкой какого-либо интервала хотя бы одного из множеств A и B ).
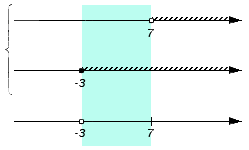
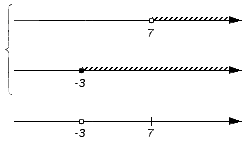
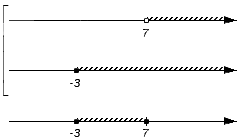
Оно является частью множества B (над интервалом присутствует штриховка), но не входит в множество A (над интервалом штриховка отсутствует): не будет входить в искомое пересечение, а значит на нижней координатной прямой не появляется никаких новых отметок:
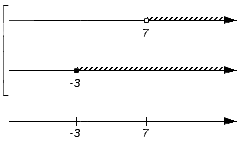
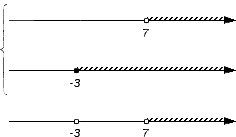
Промежуток входит в оба множества A и B (над промежутком присутствует штриховка), следовательно, становится частью пересечения. Штрихуем место над рассмотренным промежутком:
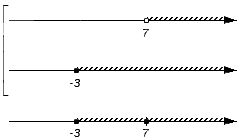
Имея некий практический опыт применения правил нахождения пересечений и объединений множеств, описанные проверки легко проводятся устно, что позволяет быстро записывать конечный результат. Продемонстрируем на практическом примере, как выглядит его решение без детальных пояснений.
Решение
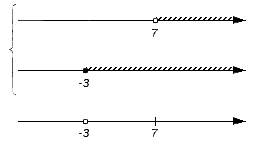
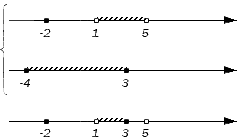
Отметим заданные числовые множества на координатных прямых, чтобы иметь возможность получить иллюстрацию искомых пересечения и объединения:
Также понятно, что при достаточном понимании процесса указанный алгоритм возможно подвергнуть оптимизации. К примеру, в процессе нахождения пересечения можно не тратить время на проверку всех промежутков и множеств, представляющих собой отдельные числа, ограничившись рассмотрением только тех промежутков и чисел, которые составляют множество А или В. Прочие промежутки в любом случае не войдут в пересечение, т.к. не являются частью исходных множеств. Составим иллюстрацию сказанного на практическом примере.
Необходимо определить пересечение исходных множеств.
Решение
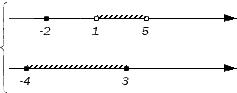
Геометрически изобразим числовые множества А и В :
Граничные точки исходных множеств разобьют числовую прямую на несколько множеств:
В заключении статьи обговорим еще, как решить задачу о нахождении пересечения и объединения нескольких множеств (более 2 ). Сведем ее, как рекомендовалось ранее, к необходимости определения пересечения и объединения первых двух множеств, затем полученного результата с третьим множеством и так далее. А можно использовать описанный выше алгоритм с единственным только отличием, что проверку вхождения промежутков и множеств, представляющих собой отдельные числа, необходимо проводить не по двум, а всем заданным множествам. Рассмотрим на примере.
Решение
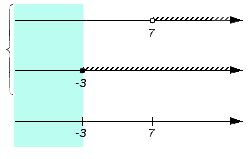
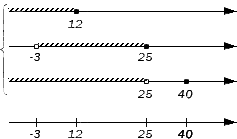
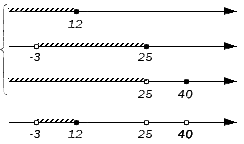
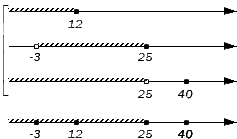
Отображаем заданные числовые множества на координатных прямых и ставим с левой от них стороны фигурную скобку, обозначая пересечение, а также квадратную, обозначая объединение. Ниже отобразим координатные прямые с отмеченными штрихами граничными точками числовых множеств:
Отметим также, что искомое пересечение числовых множеств часто является пустым множеством. Происходит это в тех случаях, когда в заданные множества не включены элементы, одновременно принадлежащие им всем.
Решение
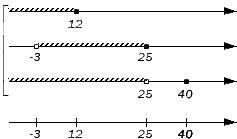
Отобразим исходные множества на координатных прямых и штрихами граничные точки этих множеств на дополнительной прямой.
Ни одно из них не является одновременно элементом всех исходных множеств, следовательно, пересечение заданных множеств есть пустое множество.
Множества удобно изображать в виде кругов, которые называют кругами Эйлера.
На рисунке множество пересечения множеств X и Y закрашено в оранжевый цвет.