Как называются концы отрезка граничными точками
Геометрия. 9 класс
Некоторые физические величины, например, сила или скорость характеризуются не только числовым значением, но и направлением. Такие величины называются векторными: F ⃗ – сила, v ⃗ – скорость.
Дадим геометрическое определение вектора.
Вектором называется отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом.
На чертежах вектор изображается отрезком со стрелкой, указывающей конец вектора. Вектор обозначают двумя заглавными латинскими буквами со стрелкой над ними. Первая буква обозначает начало вектора, вторая – конец.
Вектор можно обозначить и одной строчной латинской буквой со стрелкой над ней.
Длиной вектора называется длина отрезка, который изображает этот вектор. Для обозначения длины вектора используют вертикальные скобки.
Вектор, у которого конец совпадает с началом, называется нулевым вектором. Нулевой вектор изображается точкой и обозначается двумя одинаковыми буквами или нулём со стрелкой над ним. Длина нулевого вектора равна нулю: |0 ⃗|= 0.
Введём понятие коллинеарных векторов. Ненулевые векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считают коллинеарным любому вектору.
Докажем, что от любой точки О можно отложить вектор, равный данному вектору р ⃗, и притом только один.
Доказательство:
1) Если р ⃗ – нулевой вектор, то ОО ⃗ = р ⃗.
2) Если вектор р ⃗ ненулевой, точка Р – начало этого вектора, а точка Т – конец.
Проведём через точку О прямую, параллельную РТ. На построенной прямой отложим отрезки ОА1 и ОА2, равные отрезку РТ.
Выберем из векторов ОА1 и ОА2 вектор, который сонаправлен с вектором р ⃗. На нашем чертеже это вектор ОА1. Этот вектор будет равен вектору р ⃗. Из построения следует, что такой вектор единственный.
Вектор. Виды векторов.
Вектор — в самом элементарном случае это математический объект, который характеризуется
величиной и направлением.
В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая
из его граничных точек является началом, а какая — концом.
У вектора есть длина и определенное направление. Графически вектора изображаются как
направленные отрезки прямой конкретной длины. Длина вектора – это и есть длина этого отрезка.
Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.
Как видно на рисунке, начало отрезка – это точка А, концом отрезка является
точка В, а непосредственно вектор обозначен через 
вектора существенное значение, если переместить стрелку на другую
сторону отрезка, то получим вектор, но абсолютно другой. Понятие вектора
удобно сравнивать с движением физического тела: подумайте, ехать на
рыбалку и с рыбалки – разница огромная.

Понятия «больше» и «меньше» для векторов не имеет значения — так как направления их могут быть
разными. Сравнивают лишь длины векторов. Зато есть понятие равенства для векторов.
Виды векторов.
Единичным называется вектор, длина которого равна 1.
Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором.
У такого вектора конец и начало совпадают.
Нулевой вектор обычно обозначается как 
Коллинеарные вектора – вектора, которые параллельны одной прямой
или которые лежат на одной прямой.
Сонаправленные вектора. Два коллинеарных вектора a и b называются
сонаправленными векторами только тогда, когда их направления
соответствуют друг другу: a↑↑b

Противоположно направленные вектора – два коллинеарных вектора
a и b называются противоположно направленными векторами, только
когда они направлены в разные стороны: a↑↓b.

Компланарные вектора – это те вектора, которые параллельны одной
плоскости или те, которые лежат на общей плоскости.
В любое мгновение существует плоскость одновременно параллельную
двум любым векторам, поэтому два произвольных вектора являются

Равные вектора. Вектора a и b будут равными, если они будут лежать на
одной либо параллельных прямых и их направления и длины одинаковые.
То есть, такой вектор можно перенести параллельно ему в каждое место
Таким образом, два вектора равны, если они коллинеарные, сонаправленые
и имеют одинаковые длины:

Для координатного представления векторов огромное значение
оказывает понятие проекции вектора на ось (направленную
прямую).
проекциями точек начала и конца вектора на заданную прямую,
при этом проекции добавляется знак “+”, но когда направление
проекции соответственно направлению оси, иначе — знак “–”.

Проекция – это длина заданного вектора, умноженная на cos угла исходного вектора и оси; проекция
вектора на ось, которая перпендикулярна ему = 0.
Когда работают с векторами, зачастую вводят так называемую
декартову систему координат и уже в этой системе находят
координаты вектора по базисным векторам.
Разложение по базису геометрически можно показать проекцией
вектора на координатные оси. Когда известны координаты начала и
конца вектора, то координаты данного вектора получают вычитая
из координат конца вектора координат начала вектора.

За базис зачастую выбираются координатные орты, которые обозначаются как 
осям x, y, z. Исходя из этого, вектор 
Каждое геометрическое свойство есть возможность записать в координатах, и далее исследование
из геометрического переходит в алгебраическое и на этом этапе в основном упрощается. Обратное,
кстати, неверно: не у любого соотношения в координатах есть геометрическое толкование, но только
те соотношения, которые выполняются в любой декартовой системе координат (инвариантные).
Отрезок. Ломаная линия | Школьная математика. Математика 5 класс
Как определить принадлежит ли точка отрезку или нет? Как определить принадлежит ли точка отрезку или нет? — LISP — Программирование — Форумы
Тему читают: 1 гость
Страницы 1
Чтобы отправить ответ, вы должны войти или зарегистрироваться
Форумы CADUser → Программирование → LISP → Как определить принадлежит ли точка отрезку или нет?
Урок 31. Проверка принадлежности точки отрезку
Урок из серии «Геометрические алгоритмы»
Здравствуйте, дорогой читатель!
Сегодня мы рассмотрим еще одну типовую задачу из серии геометрические алгоритмы. Напишем функцию, которая будет проверять принадлежность произвольной точки отрезку, заданному координатами своего начала и конца.
Задача. Проверить, принадлежит ли точка отрезку.
Пусть точки 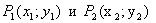
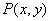
Вектор с началом в точке 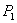
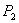
Если P(x, y) – произвольная точка, то координаты вектора 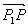
Точка Р будет принадлежать отрезку если:
Результаты выполнения программы.
Введите координаты точек: x1, y1, x2, y2, x,y
0.5 1 2.5 2.8 1.203 1.633
Да.
Результаты тестирования в программе GeoGebra:
Ввели еще две функции: EqPoint() и RealMoreEq() для реализации операций сравнения над вещественными данными. Первая проверяет, совпадают ли две точки на плоскости, вторая — используется для проверки отношения «>=».
На следующем уроке, на основе ранее написанных процедур, напишем процедуру определения координат точки пересечения двух отрезков.
На этом я с вами прощаюсь. До встречи на следующем уроке.
Источник статьи: http://gospodaretsva.com/urok-31-proverka-prinadlezhnosti-tochki-otrezku.html
Русско-английский тематический словарик
| точка | point |
| вектор | vector |
| прямая | line |
| луч | ray |
| отрезок | segment |
| угол | angle |
| окружность | circle |
| треугольник | triangle |
| прямоугольник | rectangle |
| квадрат | square |
| многоугольник | polygon |
| окружность | circle |
| медиана | median |
| биссектриса | bisector |
| высота | altitude |
| пересечение | intersection |
| длина | length |
| периметр | perimeter |
| площадь | area |
| касательная | tangent |
| скалярное произведение | dot product |
| векторное произведение | cross product |
| вектор нормали | normal vector |
| ограничивающий прямоугольник | bounding box |
0: Класс «Точка»
Реализуйте класс Pt, поддерживающих следующие операции:
print(Pt())print(Pt(1, 2))print(Pt(‘2 3’))print(Pt(1, 2) + Pt(-1, 2))print(Pt(1, 2) – Pt(-1, 2))print(3 * Pt(1, 2))print(Pt(4, 6) / 2)print(Pt(1, 2).dot(Pt(2, 1)))print(Pt(1, 2).cross(Pt(2, 1)))print(abs(Pt(3, 4)))print(Pt(1, 2) == Pt(1, 2))
(0, 0)(1, 2)(2, 3)(0, 4)(2, 0)(3, 6)(2.0, 3.0)4-35.0True
Виды числовых промежутков
В таблице a и b — это граничные точки, а x — переменная, которая может принимать координату любой точки, принадлежащей числовому промежутку.
Граничная точка — это точка, определяющая границу числового промежутка. Граничная точка может как принадлежать числовому промежутку, так и не принадлежать ему. На чертежах граничные точки, не принадлежащие рассматриваемому числовому промежутку, обозначают незакрашенным кругом, а принадлежащие — закрашенным кругом.
Могущество скалярного и косого (векторного) произведения
Сообщения 15
#1 Тема от Олег 15 июня 2004г. 11:15:36
Тема: Как определить принадлежит ли точка отрезку или нет?
Как определить принадлежит ли точка отрезку или нет?
#2 Ответ от VH 15 июня 2004г. 11:19:04
Re: Как определить принадлежит ли точка отрезку или нет?
Точка принадлежит отрезку, если сумма расстояний от этой точки до конечных точек отрезка равна длине отрезка.
#3 Ответ от AY 15 июня 2004г. 16:13:10
Re: Как определить принадлежит ли точка отрезку или нет?
#4 Ответ от Alexander 15 июня 2004г. 19:48:21
Re: Как определить принадлежит ли точка отрезку или нет?
Если устроит попробуйте использовать
функцию (vlax-curve-getParamatPoint ).
Если вернёт nil значит точка не лежит на кривой.
У Полещука написано – VLA-объект,
но как показывает практика можно и имя примитива.
#5 Ответ от kserg 15 июня 2004г. 21:25:20
Re: Как определить принадлежит ли точка отрезку или нет?
Когда-то (в AutoCAD10) выходил из положения так :
(setq Nabor (ssget “_C” t1 t1))
,- где t1 – координаты точки [например, ‘(150 175 0)],
а затем, перебирал объекты, попавшие в набор “Nabor”, на предмет наличия среди них того самого отрезка.
#6 Ответ от Leonid 15 июня 2004г. 22:08:57
Re: Как определить принадлежит ли точка отрезку или нет?
#7 Ответ от Fantomas 16 июня 2004г. 01:28:17
Re: Как определить принадлежит ли точка отрезку или нет?
Тоже недавно делал проверку принадлежности точки сфере. Естественно сравнение через EQUAL, смотря какая точность нужна.
Есть еще идея. Существует функция vlax-curve-getDistAtPoint которая вычисляет расстояние между начальной точкой кривой (а в нашем случае отрезка) до точки на кривой. В случае если точка не лежит на кривой она возвратит Nil.
Источник статьи: http://www.caduser.ru/forum/topic10577.html
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотябы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии
Геометрия 7 класс.
Точка, прямая и отрезок
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.
Точка — элементарная фигура, не имеющая частей.
Прямая состоит из множества точек и простирается бесконечно в обе стороны.
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
Граничная точка
Смотреть что такое «Граничная точка» в других словарях:
граничная точка — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] граничная точка Такая точка некоторого подмножества A метрического пространства, что любая ее малая окрестность (называется e окрестность) содержит хотя бы одну точку из A и… … Справочник технического переводчика
Граничная точка — [boundary point] такая точка некоторого подмножества A метрического пространства, что любая ее малая окрестность (называется e окрестность) содержит хотя бы одну точку из A и хотя бы одну точку, не принадлежащую A. Например. Г.т., лежащая на… … Экономико-математический словарь
граничная точка — ribinis taškas statusas T sritis fizika atitikmenys: angl. limit point; limiting point vok. Grenzpunkt, m rus. граничная точка, f; предельная точка, f pranc. point limite, m … Fizikos terminų žodynas
Граничная точка — Граница множества это такое множество, что его точки находятся сколь угодно близко как к точкам в множестве, так и к точкам вне множества. Содержание 1 Определение 2 Свойства 3 Примеры 4 См. также … Википедия
граничная точка профиля зуба — граничная точка профиля Общая точка главного или номинального профиля зуба и его переходной кривой. [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины понятия, относящиеся к зубчатому колесупрофиль зуба Синонимы граничная точка профиля … Справочник технического переводчика
граничная точка выхода — Узел, организующий вызов через внешнее соединение. Этот узел является последним в peer группе, кто работает с этим вызовом. [http://www.lexikon.ru/dict/net/index.html] Тематики сети вычислительные EN exit border node … Справочник технического переводчика
граничная точка сети — (МСЭ Т K.66). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN network boundary pointNBP … Справочник технического переводчика
ИРРЕГУЛЯРНАЯ ГРАНИЧНАЯ ТОЧКА — точка у 0 границы Г области D, для к рой существует такая непрерывная граничная функция f(y)на Г, что обобщенное решение Дирихле задачи в смысле Винера Перрона (см. Перрона метод) и (х)не принимает в точке у 0 граничного значения f(y0), т. е.… … Математическая энциклопедия
верхняя (нижняя) граничная точка однопарного зацепления — Контактная точка профиля зуба, соответствующая началу или окончанию однопарного зацепления, наиболее близкая к его вершине (к его переходной кривой). [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины параметры зубчатой передачи и… … Справочник технического переводчика








