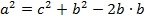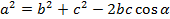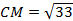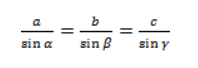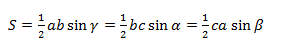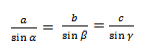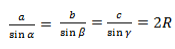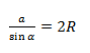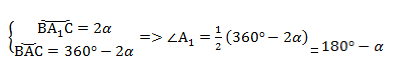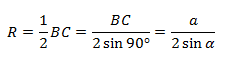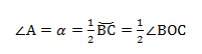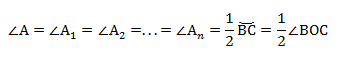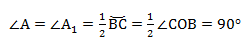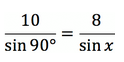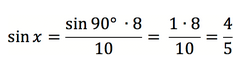теорема синусов какой класс
Геометрия. 9 класс
Докажем, что стороны треугольника пропорциональны синусам противолежащих углов.
Выразим площадь треугольника ABC через стороны и синусы углов.
S = 1/2 b c sinA, (1)
S = 1/2 a с sin B. (2)
S = 1/2 a b sin C. (3)
Приравняем первое и второе равенства:
1/2 b c sinA = 1/2 a c sin B
Умножим обе части получившего равенства на два и разделим на с:
1/2 b c sinA = 1/2 a c sinB | ∙2
b c sinA = a c sinB | :c
b sinA = a sinB
Из полученного равенства составим пропорцию – равенство отношений сторон треугольника к синусам противолежащих углов: b/sinB = a/sinA
Приравняем второе и третье равенства и проведём аналогичные преобразования:
1/2 a c sinB = 1/2 a b sinC | ∙2
a c sinB = a b sinC | :a
c sinB = b sinC
c/sinC = b/sinB (5)
Из четвёртого и пятого равенств получаем, что отношения длины стороны к синусу противолежащего угла равны: c/sinC = b/sinB = a/sinA
Около треугольника опишем окружность и выясним, как связаны отношения стороны к синусу противолежащего угла с радиусом описанной окружности.
Центр окружности, описанной около треугольника может быть расположен на стороне треугольника, внутри треугольника и вне треугольника.
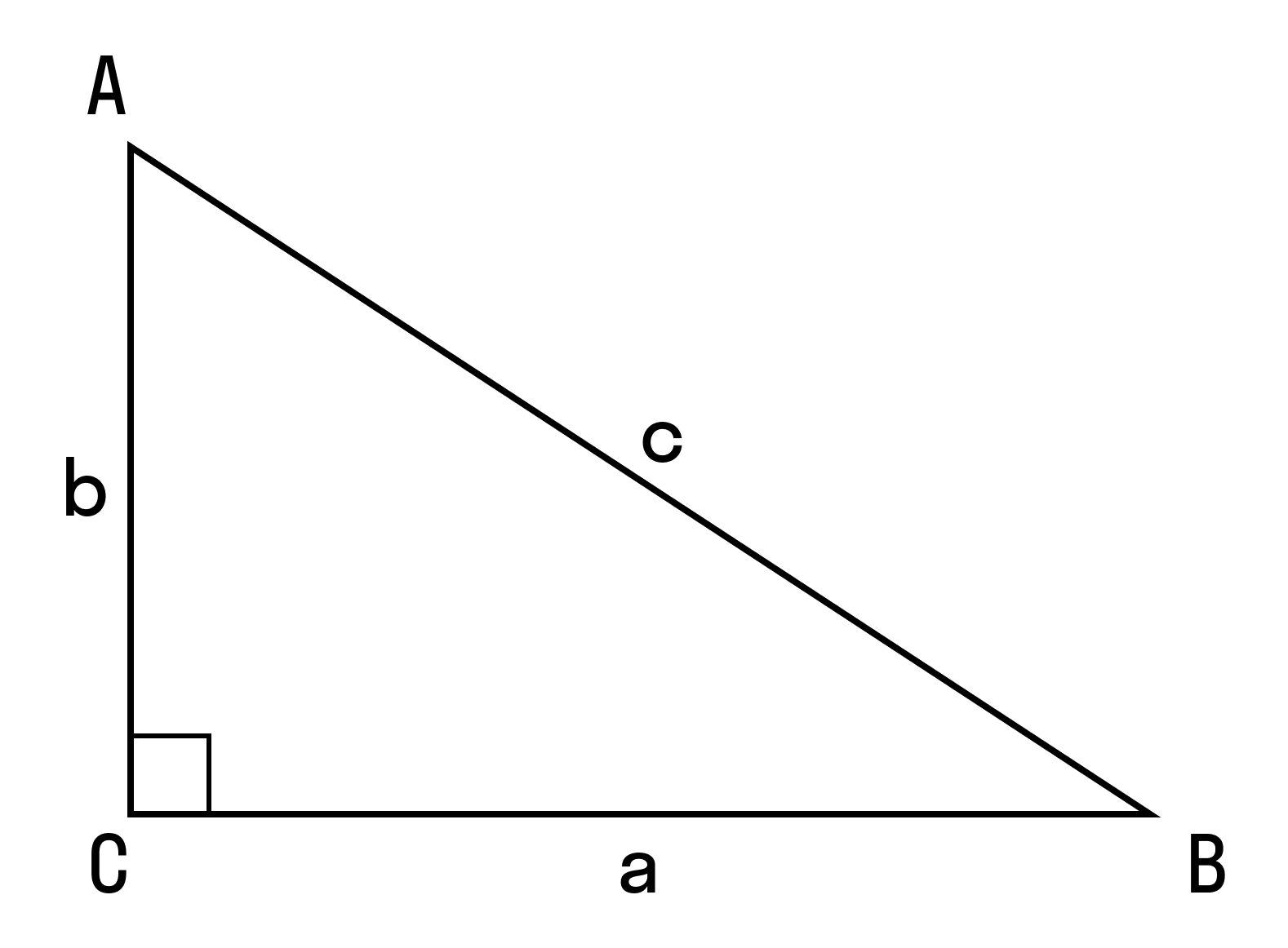
Если центр описанной окружности расположен на стороне треугольника, то этот треугольник прямоугольный.
Запишем для этого треугольника теорему синусов: c/sinC = b/sinB = a/sinА
Так как гипотенуза треугольника является диаметром окружности, а синус девяноста градусов равен единице, то отношения стороны треугольника к синусу противолежащего угла равны диаметру описанной окружности:
c/sinC = b/sinB = a/sinА = 2R/(sin90°) = 2R
Для двух других случаев.
НАШИ ПАРТНЁРЫ
© Государственная образовательная платформа «Российская электронная школа»
Урок изучения нового материала по геометрии на тему: «Теорема синусов» (9 класс)
Ищем педагогов в команду «Инфоурок»
КОУ ВО «ЦЛПДО»
БУЗ ВО «Графский санаторий для детей».
Урок изучения нового материала по геометрии
на тему: «Теорема синусов» (9 класс)
Провела учитель математики
Пешкова Галина Михайловна
Конспект урока по геометрии, изучения нового материала по теме: «Теорема синусов».
познакомить с формулировкой и доказательством теоремы синусов;
выработать у учащегося навыки решения задач с использованием тригонометрических функций;
развить умение решать треугольники.
развитие внимания, мышления, наблюдательности, активности;
развитие устной и письменной речи;
развитие умений применять полученные знания на практике.
воспитание самостоятельности, эстетичности;
воспитание интереса к предмету математики.
Метод урока: объяснительно-иллюстративный.
Тип урока: урок изучения и усвоения нового материала.
Оборудование: компьютер, раздаточный материал.
Мотивация к учебной деятельности – 1 мин.
Актуализация опорных знаний – 5 мин.
Мотивация практической необходимости рассмотрения теоремы синусов- проблемная ситуация – 7 мин.
Изучение нового материала – 10 мин.
Закрепление изученного материала – 10 мин.
Самостоятельная работа – 10 мин.
Домашнее задание – 1 мин.
1Актуализация опорных з наний
Вопросы после приветствия и орг.момента
– Чем мы занимались на прошлом уроке? (мы доказали теорему о площади треугольника)
– Какие задачи вы учились решать? (задачи на вычисление площади треугольника по двум сторонам и углу между ними)
– Сегодня на уроке мы продолжим работать с треугольником и расширим свои знания о нем.
1) Ученики решают задачи по данной теме.
Найти длину стороны ВС в треугольнике АВС, если АВ=3см, АС-4см,
В процессе решения данной и последующих задач учитель подчеркивает что решение данных задач нерациональное, эти задачи можно решить проще, если будет известна теорема, называемая теоремой синусов.
2. Дано :
Найти :
Решение : 

Фронтальный опрос: (повторение формул для вычисления площади треугольника).
а) формулы площади треугольника

б) формулы приведения


в) определение sin, cos, tg острых углов прямоугольного треугольника.
1.Найдите площадь треугольника АВС.
2.Найдите площадь параллелограмма АВСD.
3.Найдите высоту параллелограмма АВСD.
1) Предлагается решить устно задачу.
Верно ли для прямоугольного треугольника равенство: 
После того, как учащийся убедился, что в прямоугольном треугольнике стороны пропорциональны синусам противолежащих углов, ставится вопрос: «Верно ли это утверждение для любого треугольника?».
Найдите отношения сторон ВС, АВ, АС к синусам противоположных углов.
Учащиеся в группах по 4 человека работают, по окончании работы представители от групп выходят к доске и демонстрируют полученные результаты – отношения равны.
Карточка план – реализации практической работы
Выразите площадь треугольника через синус угла В, затем угла С, затем угла А. Пронумеровать равенства (1), (2), (3).
Приравняйте 1 и 2 равенства, разделите полученное равенство на (½ВС).
Запишите полученное равенство и составьте пропорцию: равенство. отношений сторон треугольника к синусам противолежащих углов.
Аналогично, приравняйте 2 и 3 равенства и проделайте аналогичные шаги.
– Найдите отношения сторон ВС, АВ, АС к синусам противоположных углов и докажите, что они равны.
– Что вам придется доказывать? (равенство отношений)
– Как называется утверждение, которое требуется доказать? (теорема)
– Сформулируйте тему урока. (Доказать теорему о том, что отношения сторон к синусам противолежащих углов равны)
– В геометрии эта теорема называется теоремой синусов.
Историческая справка. Впервые эту теорему доказал выдающийся азербайджанский учёный Насирэддин Туси (1201-1274гг.)
Тема записывается на доске и в тетрадях «Теорема синусов». (Практическая работа – это и есть доказательство теоремы синусов).
Объяснение нового материала.
1) Теорема: Стороны треугольника пропорциональны синусам противолежащих углов.
Дано: Пусть в 
Доказать: 
По теореме о площади треугольника

Из первых двух равенств получаем 



Теорему можно записать и в другом виде:
Итак, мы доказали теорему синусов.
Запишите теорему синусов для треугольников:
В теореме синусов в том виде, в каком мы ее получили, присутствует недоговоренность : мы узнали, что отношения сторон к синусам противолежащих им углов равны между собой, но чему же именно равны эти отношения?
Чтобы ответить на этот вопрос, обратимся к задаче №1033.
Вывод: если в треугольнике против сторон a , b , c лежат углы α, β, γ соответственно, то 
где R – радиус окружности, описанной около треугольника.
Таким образом, мы получили дополнительное правило отыскания радиуса описанной около треугольника окружности .
Чем вы сейчас будете заниматься? (будем выполнять задание, где используется теорема синусов)
1) Работа с учебником
Самостоятельная работа с самопроверкой по эталону.
На экране эталон решения.
Выразите х и у через синусы острых углов.
Ответ:
Выяснить у кого какие результаты.
Кто и где допустил ошибку.
Выразите х и у через синусы острых углов.
Рефлексия учебной деятельности на уроке.
– Какую цель вы ставили перед собой на уроке? – Вы достигли поставленной цели?
– Что помогало выполнять задание? – Проанализируйте свою работу на уроке, заполнив карточку.
Карточка для этапа рефлексии.
Ответьте на вопросы:
Данная тема мне понятна. Я хорошо понял теорему синусов.
Я знаю, как пользоваться теоремой синусов. В самостоятельной работе у меня все получилось.
Теорема косинусов и синусов
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
К полученному выражению прибавим и отнимем квадрат второго катета:
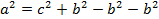
Но так как b = c * cos α, то
Эту формулу мы получили для катетов в прямоугольном треугольнике, но аналогичная связь между стороной а и косинусом противолежащего угла справедлива и для произвольного треугольника.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
Что и требовалось доказать.
Следствие из теоремы косинусов: теорему косинусов также можно использовать для определения косинуса угла треугольника:
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
Приравниваем правые части уравнений:
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
Таким образом, теорема косинусов обобщает теорему Пифагора. Закон косинуса может быть использован для любого вида треугольника.
Описание формулы косинуса угла из теоремы косинусов
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
Теорема синусов
Доказательство теоремы синусов
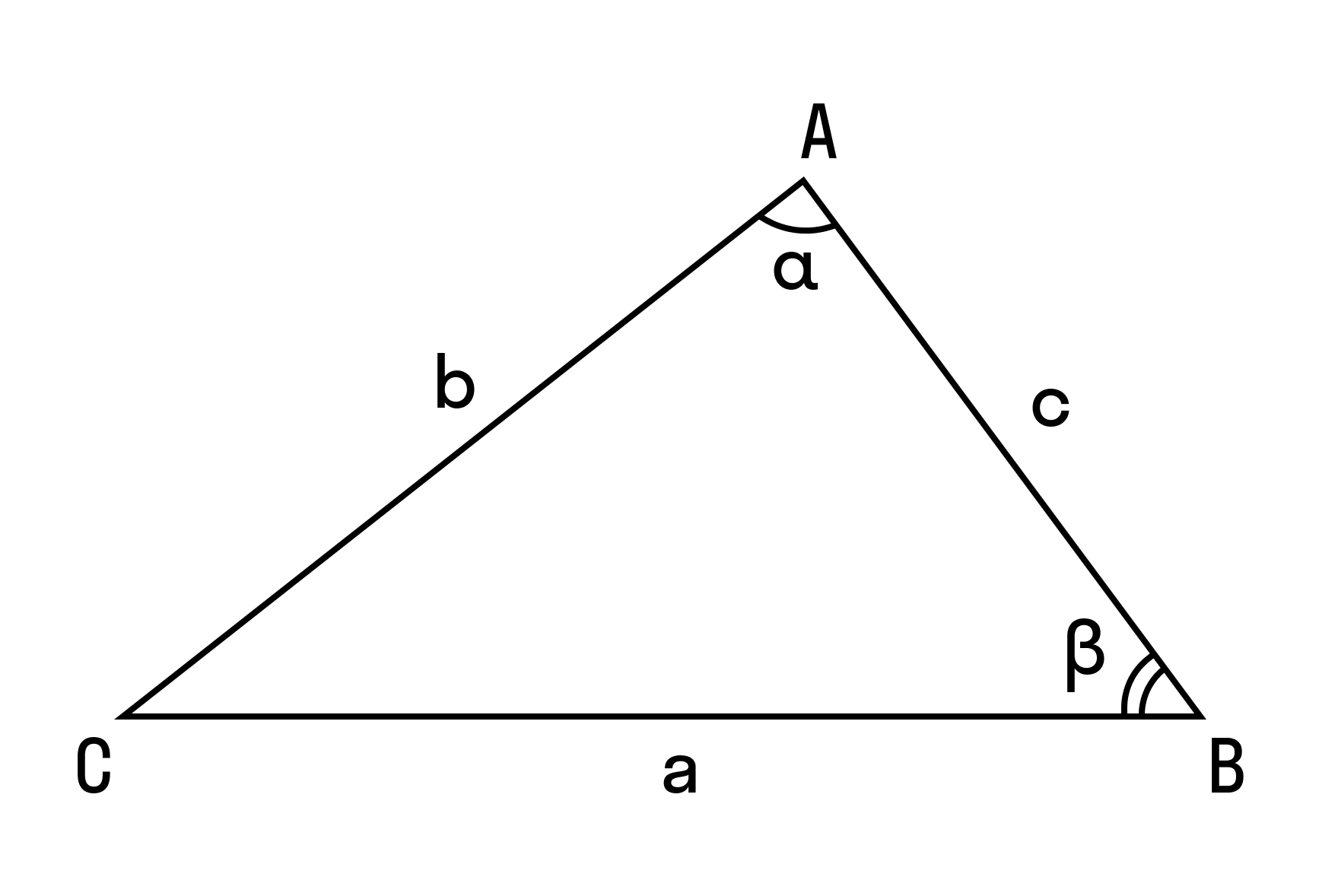
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
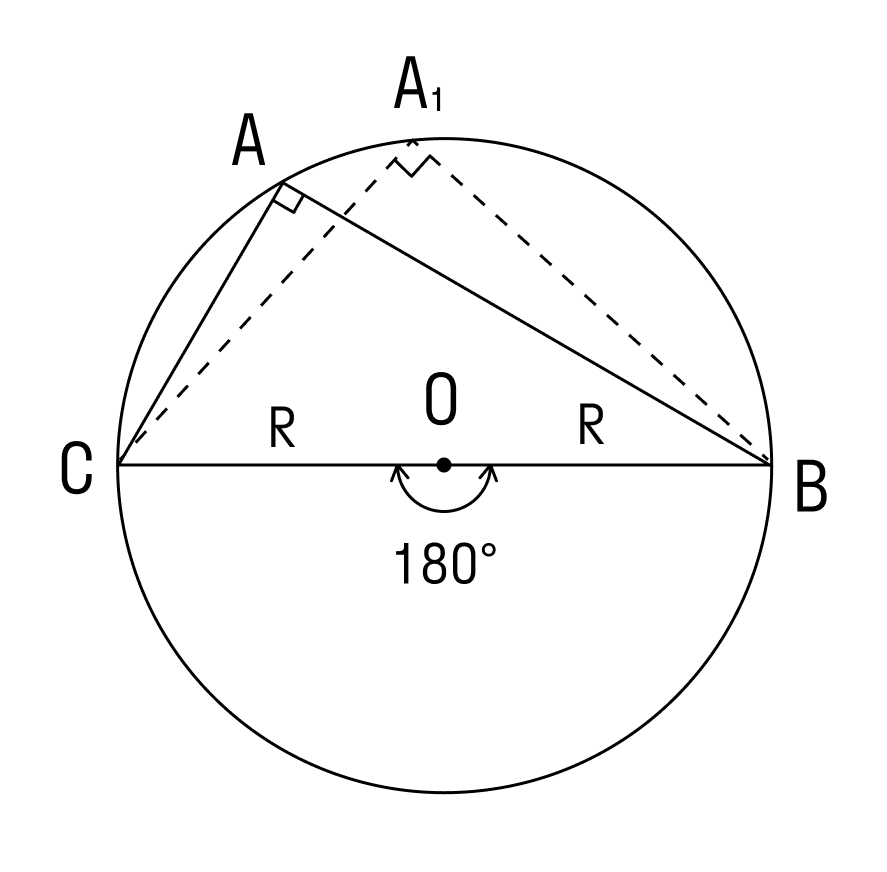
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Вспомним свойство вписанного в окружность четырёхугольника:
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
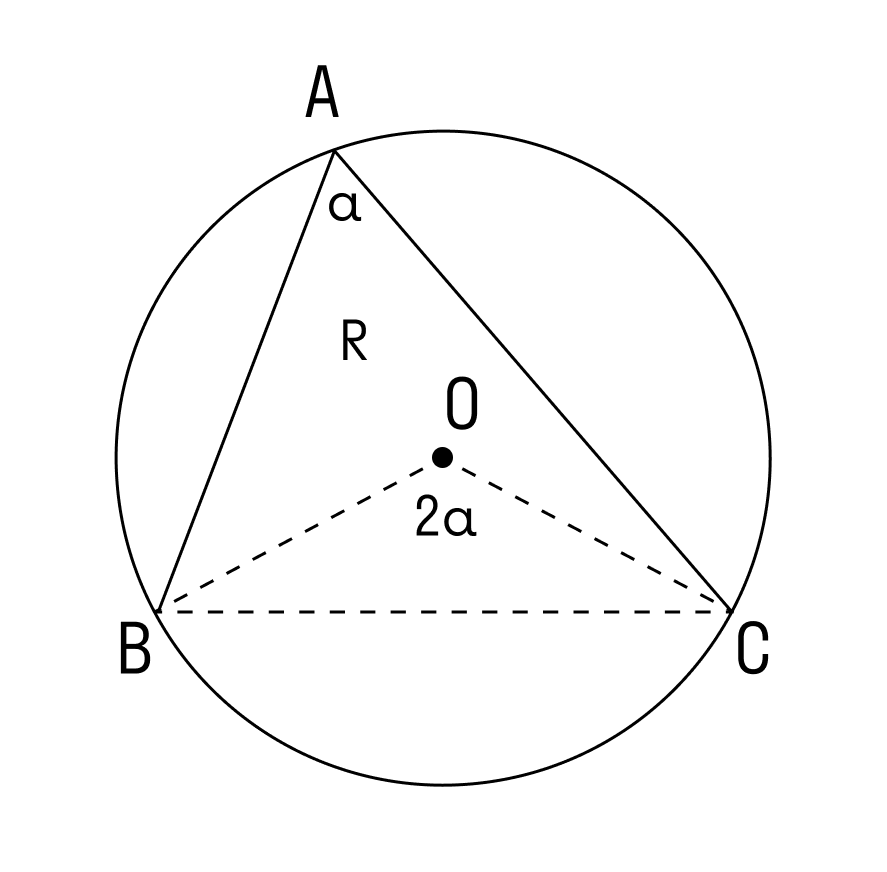
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)