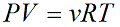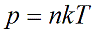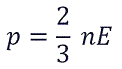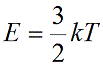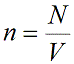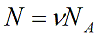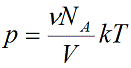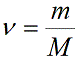уравнение менделеева клапейрона в каком классе проходят

Отважнее! В область хаоса!

Урок физики 10 класс

Учитель Гребенюк Л.И.

Хезеф Луи Гей-Люссак

Уравнение состояния идеального газа

Для любого газа зависимость этих величин выглядит так:

Уравнением состояния идеального газа

Уравнением Клапейрона (1834г)

Клапейрон Бенуа Поль Эмиль

Универсальная газовая постоянная

Умножим обе части уравнения на ν = m/M

Менделеев Дмитрий Иванович

Обобщив уравнение Клапейрона,

в 1874 вывел общее уравнение состояния идеального газа

Для чего это нужно

( Будет изучаться в конце раздела «Молекулярная физика»)

1.Чему равен объем, который занимает водород массой 1 кг при температуре 27 ºС и давлении 100 кПа?

2.При давлении 100000 Па и температуре 27 ºС плотность газа равна 0, 162 кг/ м 3 Определите какой это газ?

Источник

Ищем педагогов в команду «Инфоурок»

Разработка урока физике в 10 классе на тему « Уравнение Клапейрона-Менделеева».

Развивающие. Формировать умение выражать свои мысли правильным «физическим» языком. Формировать умение выделять главное, обобщать и связывать имеющиеся знания со знаниями из других областей. Формировать умение наблюдать и анализировать явления, кратко и лаконично отвечать на вопросы.

Тип урока : изучение нового материала, с использованием элементов беседы.

Демонстрации: зависимость между объемом, давлением и температурой.

Оборудование : мульдимедийный проектор, компьютер.

Проверка домашнего задания. Повторение ранее изученного. ( фронтальный опрос).

-Почему барабанная перепонка уха не продавливается бомбардирующими её молекулами воздуха?

-Что доказал эксперимент Отто фон Герике?(опыт с Магдебурскими полу шариами)(слайд).

— Сформулируйте закон Дальтона. ( Давление смеси газов, не взаимодействующих друг с другом химически, равно сумме парциальных давлений этих газов. Воздух в комнате, где мы находимся, представляет собой смесь нескольких газов, в основном — азота (около 80%) и кислорода (около 20%).)

— Что такое идеальный газ?

-Назовите условия, при которых газ можно считать идеальным?

— Что называется концентрацией?

-Сформулируйте и запишите основное уравнение молекулярно-кинетической теории газов.

— Назовите макропараметры, характеризующие газ? ( p – давление, V – объем, T – температура. )

Рассказ учителя. Температуру, объем, давление и некоторые другие параметры принято называть параметрами состояния газа. Выведем уравнение, устанавливающее зависимость между этими параметрами.

В 1834 году французский физик Б.Клайперон( презентация),работавший длительное время России,вывел уравнение состояния идеального газа при постоянной массе. Это уравнение связывает давление,объём и температуру,которые определяют состояние идеального газа,и называется уравнением состояния идеального газа.

Для постоянной массы идеального газа отношение произведения давления на объём к данной температуре есть величина постоянная.

P ₁ V ₁ / T ₁ = P ₂ V ₂ / T ₂ ; P ₀ V ₀ / N ₀ =8,31 Д ж/моль*К –универсальная газовая постоянная для одного моля газа при нормальных условиях.

В 1874году Д.И.Менделеев(презентация) вывел уравнение для произвольного числа молекул.

N = m / m ₀ ; N = m /µ N _а ; pV = NkT ; PV = m /µ N _a kT

pV=m/µ R T — уравнение Менделеева – Клапейрона.

1.Что называют уравнением состояния системы?

2.Записать уравнение Клапейрона-Менделеева для произвольной массы идеального газа.

3.Чему равна универсальная газовая постоянная?

4.Каков физический смысл универсальной газовой постоянной?

5.Как запишется уравнение состояния для одного моля газа?

1.В сосуде вместимостҗю 500см 3 содерңится 0,89г водорода при температуре 17 0 С.Определите давление газа.

2.В баллоне емкостҗю 25,6л находится 1,04 кг азота при давлении 3,5 МПа.Определитҗ температуру газа.

3.Какой объём занимает газ в количестве 10 3 мол ь при давлении 1 МПА и температуре 100 0 С?

4.Найти плотность водорода при температуре 15 0 С и давлении98кПа.

Источник

План-конспект открытого урока «Уравнение Менделеева-Клапейрона»

При проведении урока используются активные формы и методы работы

Просмотр содержимого документа
«План-конспект открытого урока «Уравнение Менделеева-Клапейрона»»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН

УПРАВЛЕНИЕ ОБРАЗОВАНИЯ ВОСТОЧНО-КАЗАХСТАНСКОГО ОБЛАСТНОГО АКИМАТА

КГУ «ИНДУСТРИАЛЬНО-ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖ»

Методическая разработка открытого урока

тема: «Уравнение Менделеева-Клапейрона»

Специальность: 1201000 «Техническое обслуживание, ремонт и эксплуатация автомобильного транспорта»

Квалификация: 1201072 «Слесарь по ремонту автомобилей»

Преподаватель: Тихоненко С.А.

Рассмотрено на заседании ПЦК Согласовано

Общеобразовательных дисциплин Председатель УМО преподавателей

Протокол №2 от 9 сентября 2019 г физики и математики

Председатель ПЦК ООД _____________ Сапаргалиева Г.С.

____________ Тихоненко С.А. «_____» октября 2019 г.

Внедрение инновационных технологий, сотрудничество, сотворчество обеспечивает возможность усвоения системы научных понятий, которая позволяет учащимся стать реальными субъектами учения. Технологии активных форм обучения, КМ, ИКТ используются, чтобы организовать и поддерживать учебную активность учащихся. Обучение учащихся выбору, поиску наиболее рационального способа решения, не навязывая единственный путь, по которому им следует идти, создание комфортных условий для сравнительно самостоятельного разрешения учащимися проблем являются прочной основой для формирования у них интеллектуальных навыков, творческого мышления.

Урок направлен на реализацию требований нового стандарта и концепции личностно-ориентированного обучения, на обеспечение формирования важнейшей компетенции личности – умения учиться. Учебный процесс на занятии организуется так, что в групповой работе, в процессе самостоятельной познавательной деятельности, организованной учителем, учащиеся овладевают системой знаний и умений, востребованных в повседневной жизни. Они измеряют физические величины, проводят опыты и экспериментальные исследования, создают знаковые и математические модели, применяют физические знания на практике.

Данный урок нацелен на развитие работы учащихся в команде и индивидуально, призван расширить мировоззрение студентов в области молекулярной физики посредствам применения новых информационных технологий, развивать умения и навыки выделять главное, обобщать знания по предмету, формировать компетентность и информационную культуру учащихся, активизировать внимание и познавательный интерес к предмету.

Опорными знаниями являются: Уравнение Клапейрона-Менделеева, формулы для вычисления объема, плотности и числа молекул.

Были обеспечены условия для создания ситуации успеха для каждого учащегося.

Ожидаемые результаты. После изучения данной темы учащиеся должны: знать уравнение Клапейрона-Менделеева; понимать смысл и его всеобщий характер; уметь применять уравнение в конкретных случаях при решении задач и тестировании; вычислять давление, массу газа, объем, температуру; знать числовое значение универсальной газовой постоянной; уметь вычислять массу газа и число молекул в нем.

Критерии оценки. Используется рейтинговая система оценки с автоматическим переводом баллов в отметки по 5-ти бальной системе.

Тема урока: Уравнение Менделеева-Клапейрона.

Показать математическую зависимость между тремя макроскопическими параметрами p,V,T. Учить применять физические законы при решении задач. Научить применять полученные знания как язык науки, имеющий огромные возможности.

Формировать умение выделять главное, обобщать и связывать имеющиеся знания со знаниями из других областей.

Дать возможность почувствовать свой потенциал каждому учащемуся, чтобы показать значимость полученных знаний. Побудить к активной работе мысли. Развивать кругозор учащихся

Тип урока: комбинированный

Методы обучения: репродуктивный, учебно-познавательная деятельность учащихся, применение технологии сотрудничества и интегрированного обучения.

Форма проведения урока: групповая работа, индивидуальная работа.

СОТ: Развитие критического мышления, ИКТ.

Оборудование: компьютер, интерактивная доска, презентация, доска для записи формул, раздаточный материал.

Проверка домашнего задания – кластер 7 мин.

Объяснение новой темы – 20 мин.

Историческая справка о Д.И. Менделееве и Б. Клапейроне.

Работа с текстом – метод помет.

Домашнее задание. – 2 мин.

1. Организационный момент:

Приветствие учащихся, проверка готовности группы к уроку, наличие необходимых принадлежностей. Постановка целей и задач урока. Дерево ожиданий.

2.Проверка домашнего задания.

Создание кластера по группам:

Основное уравнение МКТ.

Основные положения МКТ.

3.Объяснение новой темы.

Историческая справка о Д.И. Менделееве и Б. Клапейроне – сообщение учащихся (опережающее задание).

Просмотр видеофрагмента «Связь между давлением, объёмом и температурой».

Работа с текстом. Метод помет.

Уравнение состояния идеального газа Менделеева-Клапейрона с выводом

Уравнение состояния идеального газа показывает корреляцию его основных макропараметров, а именно: объема V, давления P, а также температуры T.

R – универсальная газовая постоянная, 8,31 [Дж/(моль · К)]

Данную формулу также называют уравнением Менделеева-Клапейрона для идеального газа в честь двух ученых впервые получившего (Бенуа Клапейрон (1799 – 1864)) и применившего (Дмитрий Иванович Менделеев (1834 – 1907)) его.

Вывод уравнения Менделеева-Клапейрона

Давление идеального газа зависит от концентрации частиц и температуры тела:

Т – абсолютная температура, в кельвинах [К]

Возьмем основное уравнение МКТ, выведенное через кинетическую энергию:

Подставим nkT вместо давления и выразим кинетическую энергию:

Концентрация частиц газа n равна:

N – число молекул газа в емкости объемом V [м 3 ]. N также можно представить как произведение количества вещества ν и числа Авогадро NA:

Подставим эти величины в уравнение давления идеального газа (p=nkT):

Произведение числа Авогадро N_A и константы Больцмана k дает универсальную газовую постоянную R, которая равна 8,31 [Дж/(моль · К)].

Используя это, упростим уравнение давления и получим искомое уравнение состояния идеального газа:

Учитывая, что количество вещества ν также можно определить, если известны масса вещества m и его молярная масса M:

можно привести уравнение к следующему виду:

Частными случаями уравнения являются газовые законы, описывающие изопроцессы в идеальных газах, т.е. процессы, при которых один из макропараметров (T, P, V) в закрытой изолированной системе постоянный. Всего этих частных случаев 3.

О них мы будем говорить на следующем уроке.

Закрепление. Кубик Блума.

Выразить из уравнения Менделеева-Клапейрона следующий параметр:

Давление, объём, температура, масса, молярная масса, количество вещества.

Домашнее задание. Решение задач.

Работа по таблице «Определение недостающих величин»
В таблице приведены значения некоторых параметров состояния газа.

Определить недостающие параметры.

Источник

Урок-открытие с элементами исследования. Уравнение состояния идеального газа.

Разделы: Физика

Урок проводится в 10 классе, после изучения темы основное уравнение МКТ. (рассчитан на профильный уровень, слайд 0)

Цели урока:

Тип урока: изучение нового материала, с использованием элементов беседы.

Эпиграф к уроку:

«Посев научный взойдет для жатвы народной!»
(Дмитрий Иванович Менделеев) (слайд 1)

Демонстрации: зависимость между объемом, давлением и температурой.

Оборудование: мульдимедийный проектор, компьютер, экран, презентация PowerPoint.

Ход урока

I. Проверка домашнего задания. Повторение ранее изученного. (фронтальный опрос)

Учитель. Здравствуйте ребята. Добрый день. Выполним с вами экспериментальную задачу. Определим атмосферное давление в нашем кабинете. Оборудование: термометр, линейка (рассуждения учащихся).

Ученик. Термометром можно измерить температуру, линейкой измерить размеры комнаты и вычислить объем. А как установить зависимость между давлением, объемом и температурой?

Учитель. И это будет целью нашего урока, вывели физический закон, устанавливающий зависимость между тремя макроскопическими параметрами — p, V, T; научиться использовать закон при решении задач.

Учитель. Что такое идеальный газ? (слайд 2)

Ученик. Идеальным газом называется модель реального газа. Молекулярно-кинетическая теория рассматривает идеальный газ как множество частиц (молекул), расстояние между которыми намного превышает размеры самих частиц, находящихся в состоянии непрерывного хаотичного движения.

Учитель. Назовите условия, при которых газ можно считать идеальным?

Ученик. Газ, удовлетворяющий следующим условиям:

Учитель. Что называется концентрацией?

Ученик. Концентрация – это число молекул в единице объема.

Учитель. Запишите и объясните физический смысл основного уравнения молекулярно-кинетической теории.

II. Постановка проблемного вопроса и решение его

Учитель. Какие параметры, характеризующие газ и процессы, проходящие в нем, называются микроскопическими параметрами (микропараметрами).

Ученик. Состояние идеального газа и процессы, проходящие в нем, будут определяться количеством частиц (молекул), из которых состоит газ, и их параметрами, такими как масса, диаметр, скорость, энергия и пр. (слайд 4) Такие параметры называются микроскопическими или микропараметрами.

Учитель. Какие параметры, характеризующие газ, и процессы, проходящие в нем, называются макроскопическими параметрами (макропараметрами)? (слайд 5)

Ученик. Параметры, характеризующие свойства газа как целого называются макроскопическими или макропараметрами.

Учитель. Если состояние газа не меняется, то не меняются и эти параметры. Назовите макропараметры, характеризующие газ?

Ученик. p – давление, V – объем, T – температура.

Учитель. Температуру, объем, давление и некоторые другие параметры принято называть параметрами состояния газа. Выведем уравнение, устанавливающее зависимость между этими параметрами. (слайд 6)

III. Изучение нового материала

1. Постоянная Лошмидта. Из основного уравнения МКТ идеального газа можно получить уравнение состояния идеального газа, связывающее между собой параметры состояния p, V и Т.

p=nkT (1)

Это соотношение позволяет по двум известным макроскопическим параметрам (давлению и температуре газа) оценить микроскопический параметр (концентрацию).

Найдем концентрацию молекул любого идеального газа при нормальных условиях (н.у.):

Это значение концентрации молекул идеального газа при нормальных условиях называется постоянной Лошмидта.

2. Уравнение Клапейрона.

Получим теперь с помощью равенства (1) новое уравнение. Если известно полное число частиц газа N, занимающего объем V, то число частиц в единице объема

С учетом этого выражение (1) приводится к виду

Для постоянной массы идеального газа отношение произведения давления на объем к данной температуре есть величина постоянная.

Выведенное нами уравнение связывает давление, объем и температуру, которые определяют состояние идеального газа, называется уравнением состояния идеального газа. – уравнение Клапейрона (слайд 7)

Историческая справка. (сообщение ученика, Приложение 1) В 1834 г. Французский физик Б. Клапейрон, работавший длительное время в России (Петербурге), вывел уравнение состояние идеального газа при постоянной массе газа (m=const).(слайд 8)

3. Уравнение Менделеева – Клапейрона.

Рассмотрим случай для произвольной массы газа

R=kN_A = 8,31Дж/( моль·К) — универсальная газовая постоянная.

pV=m/M R T — уравнение Менделеева – Клапейрона- уравнение состояния идеального газа, связывающее три макроскопических параметра (давление, объем и температуру) газа данной массы. (слайд 9)

Историческая справка. (сообщение ученика, Приложение 2) Обобщив уравнение Клапейрона и введя понятие универсальной газовой постоянной, русский ученый Д. И. Менделеев в 1874 г.вывел общее уравнение для состояния идеального газа. (уравнение Менделеева – Клапейрона) (слайд 10)

С помощью данного уравнения можно описывать процессы сжатия и расширения, нагревания и охлаждения идеального газа.

IV.Закрепление изученного материала

1. Беседа с учащимися по вопросам. (слайд 11)

Учитель. Каковы нормальные условия для идеального газа?

Ученик. Нормальные условия для идеального газа: атмосферное давление p=1,013·10 5 Па, температура t=0°С, или Т=273,15К:

Учитель: Какова концентрация молекул идеального газа при нормальных условиях?

Учитель: Какие величины характеризуют состояние газа?

Ученик: Макропараметры p, V, T.

Ученик: Уравнение состояния идеального газа для постоянной массы газа. Уравнение Менделеева – Клапейрона для переменной массы газа

Учитель. Чему равна универсальная газовая постоянная в СИ?

Ученик. R=N_Ak= 8,31Дж/ моль·К – универсальная газовая постоянная

2. Решение задач у доски с помощью учителя. (слайд 12)

Дополнительная задача. Для постоянной массы идеального газа отношение произведения давления на объем к данной температуре есть величина постоянная.

Вычислите отношение произведения давления на объем к данной температуре, если газ находиться при нормальных условиях

R=8,31 Дж/(моль·К) –универсальная газовая постоянная.

V. Итоги урока

Ученик. Поставленной цели мы достигли: вывели физический закон, устанавливающий зависимость между тремя макроскопическими параметрами — p, V, T; и использовали его при решении задач.

А завершить урок хотелось словами Д.И. Менделеева, обращенными к нам, его потомкам: «Посев научный взойдет для жатвы народной!». И этот год юбилейный, 175-лет со дня рождения великого русского ученого-естествоиспытателя Д.И. Менделеева (слайд 14).

VI. Домашнее задание

§ 53, задачи 2, 5 к § 53.

Презентация — Приложение 4, сообщение ученика о Клапейроне — Приложение 1, сообщение ученика о Менделееве — Приложение 2, задачи для закрепления пройденной темы — Приложение 3.

Источник

Ищем педагогов в команду «Инфоурок»

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Приложение 3.docx

Выбранный для просмотра документ Приложение 4.docx

Выбранный для просмотра документ Приложение 5.docx

Выбранный для просмотра документ Технологическая карта урока.docx

ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА ФИЗИКИ

ОУ: Муниципальное казенное общеобразовательное учреждение Венгеровская СОШ№ 2.

Учитель: Любчикова Любовь Николаевна, учитель физики.

УМК: Г.Я. Мякишев, Б.Б. Буховцев Физика 10 класс. М.: Просвещение, 2018.

Тема урока: Уравнение состояния идеального газа

Тип урока: Изучение нового материала и первичного закрепления

Цель урока: Создание условий для осознания и осмысления уравнения состояния идеального газа.

Ø установить связь между макроскопическими параметрами состояния вещества, ознакомить со следствиями, вытекающими из уравнения состояния идеального газа; формировать умения применять полученные знания при решении задач.

Ø развивать навыки анализа информации, развивать мышление и мировозрение обучающихся через использование метода научного познания; осуществление межпредметных связей с математикой и химией при выводе уравнения состояния идеального газа, развивать навыки самообразования.

Ø способствовать развитию интереса к физике, повышать уровень мотивации, воспитывать культуру общения.

Формы организации познавательной деятельности учащихся : фронтальная, групповая, индивидуальная.

Методы обучения: проблемное изложение, частично поисковый (эвристический).

Основные понятия: идеальный газ, температура, давление, объем, уравнение состояния идеального газа, универсальная газовая постоянная.

Межпредметные связи: математика, химия.

Источник