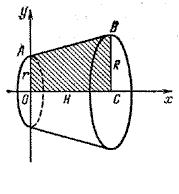
V abh формула чего
Объем прямоугольного параллелепипеда
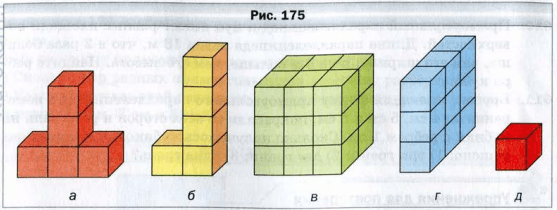
Фигуры на рисунке 175, а и б состоят из равного количества одинаковых кубиков. О таких фигурах можно сказать, что их объемы равны. Прямоугольные параллелепипеды, изображенные на рисунке 175, в и г, состоят соответственно из 18 и 9 одинаковых кубиков. Поэтому можно сказать, что объем первого из них в два раза больше объема второго.
С такой величиной, как объем, вы часто встречаетесь в повседневной жизни: объем топливного бака, объем бассейна, объем классной комнаты, показатели потребления газа или воды на счетчиках и т.д.
Опыт подсказывает вам, что одинаковые емкости имеют равные объемы. Например, одинаковые бочки имеют равные объемы.
Если емкость разделить на несколько частей, то объем всей емкости равен сумме объемов ее частей. Например, объем двухкамерного холодильника равен сумме объемов его камер.
Эти примеры иллюстрируют следующие свойства объема фигуры.
1 ) Равные фигуры имеют равные объемы.
2 ) Объем фигуры равен сумме объемов фигур, из которых она состоит.
Как и в случаях с другими величинами (длина, площадь), следует ввести единицу измерения объема.
За единицу измерения объема выбираю куб, ребро которого равно единичному отрезку. Такой куб называют единичным.
Измерить объем фигуры − значит подсчитать, сколько единичных кубов в ней помещается.
Если объем красного кубика (см. рис. 175, д) принять за единицу, то объемы фигур на рисунке 175, а, б, в и г соответственно равны 5, 5, 18 и 9 кубических единиц.
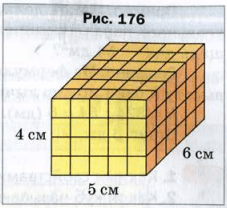
Объем прямоугольного параллелепипеда равен произведению трех его измерений.
V = abc
Поскольку у куба все ребра равны, то его объем вычисляют по формуле:
V = a 3
где a − длина ребра куба. Именно поэтому третью степень числа называют кубом числа.
Итак, мы получили еще одну формулу для вычисления объема прямоугольного параллелепипеда:
V = Sh
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
Решение. Из формулы V = Sh следует, что h = V : S. Тогда искомую высоту h бака можно вычислить так:
Архимедова сила
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сила: что это за величина
Прежде чем говорить о силе Архимеда, нужно понять, что это вообще такое — сила.
В повседневной жизни мы часто видим, как физические тела деформируются (меняют форму или размер), ускоряются и тормозят, падают. В общем, чего только с ними не происходит! Причина любых действий или взаимодействий тел — ее величество сила.
Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел. Сила измеряется в ньютонах — единице измерения, которую назвали в честь Исаака Ньютона.
Поскольку сила — величина векторная, у нее, помимо модуля, есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В этом случае результат выражается в направлении движения.
Открытие закона Архимеда
Так вышло, что закон Архимеда известен не столько своей формулировкой, сколько историей возникновения.
Легенда гласит, что царь Герон II попросил Архимеда определить, из чистого ли золота сделана его корона, при этом не причиняя вреда самой короне. То есть расплавить корону или растворить — нельзя.
Взвесить корону Архимеду труда не составило, но этого было мало — нужно ведь определить объем короны, чтобы рассчитать плотность металла, из которого она отлита.
Рассчитать плотность металла, чтобы установить, золотая ли корона, можно по формуле плотности.
Формула плотности тела
ρ = m/V
ρ — плотность тела [кг/м 3 ]
m — масса тела [кг]
V — объем тела [м 3 ]
Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. Тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему.
Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый закричал «Эврика!» и побежал докладывать о своей победе в царский дворец (и так торопился, что даже не оделся). 🤦🏻♂️
Формула и определение силы Архимеда для жидкости
На поверхность твердого тела, погруженного в жидкость, действуют силы давления. Эти силы увеличиваются с глубиной погружения, и на нижнюю часть тела будет действовать со стороны жидкости большая сила, чем на верхнюю.
Равнодействующая всех сил давления, действующих на поверхность тела со стороны жидкости, называется выталкивающей силой или силой Архимеда. Истинная причина появления выталкивающей силы — наличие различного гидростатического давления в разных точках жидкости.
Определение архимедовой силы для жидкостей звучит так:
Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю весу вытесненной жидкости и противоположно ему направлена.
Формула архимедовой силы для жидкости
ρж — плотность жидкости[кг/м 3 ]
Vпогр — объем погруженной части тела [м 3 ]
g — ускорение свободного падения [м/с 2 ]
А теперь давайте порешаем задачки, чтобы закрепить, как вычислить архимедову силу.
Задача 1
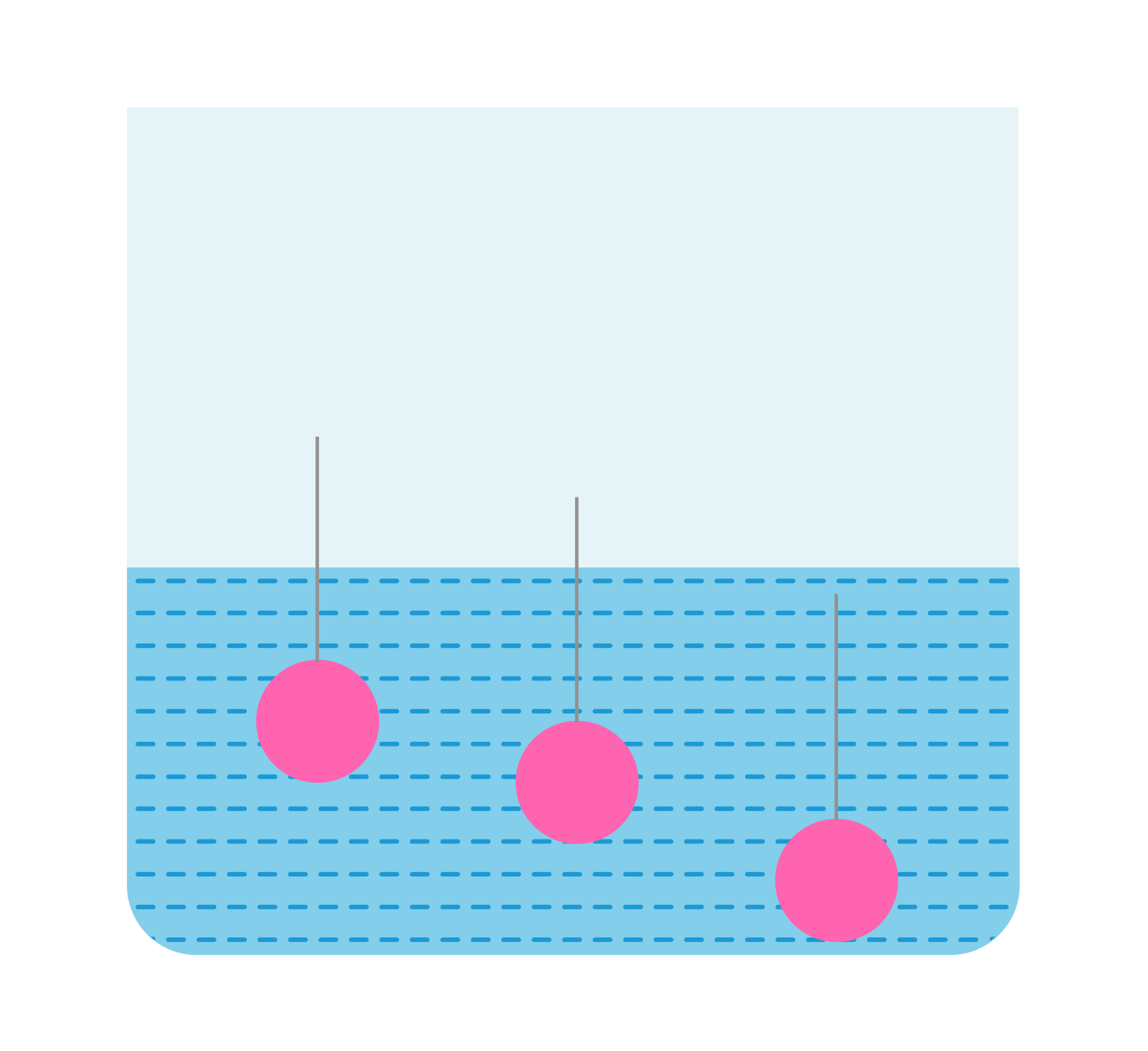
В сосуд погружены три железных шарика равных объемов. Одинаковы ли силы, выталкивающие шарики? Плотность жидкости вследствие ничтожно малой сжимаемости на любой глубине считать примерно одинаковой.
Решение
Да, так как объемы одинаковы, а архимедова сила зависит от объема погруженной части тела, а не от глубины.
Задача 2
Решение
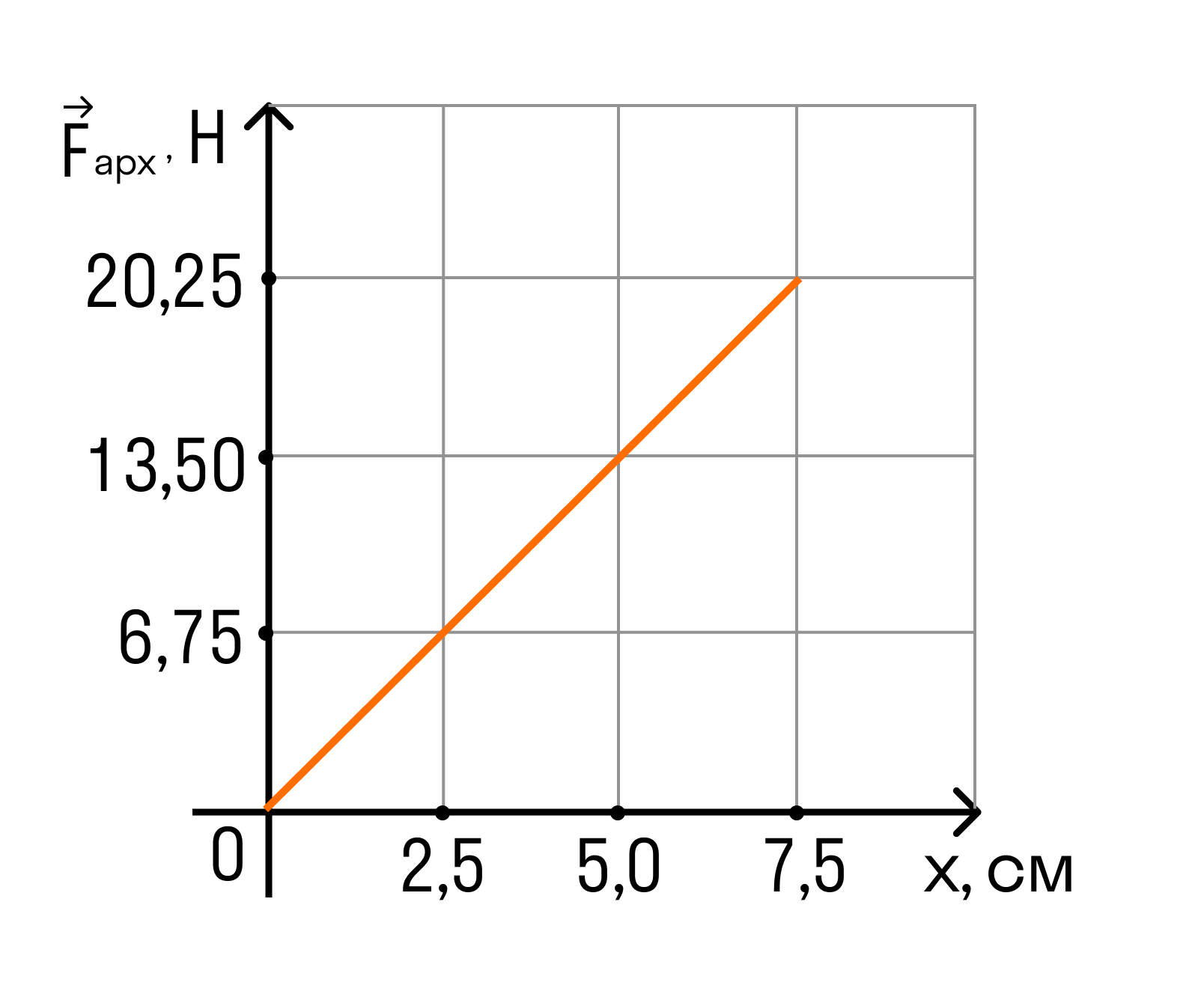
Сила Архимеда, действующая на кубик, равна FАрх = ρжgVпогр.
Vпогр. — объем погруженной части кубика,
ρж — плотность жидкости.
Учитывая, что нижнее основание кубика все время параллельно поверхности жидкости, можем записать:
где а — длина стороны кубика.
Рассматривая любую точку данного графика, получим:
Условия плавания тел
Из закона Архимеда вытекают следствия об условиях плавания тел.
Погружение
Плавание внутри жидкости
Плавание на поверхности жидкости
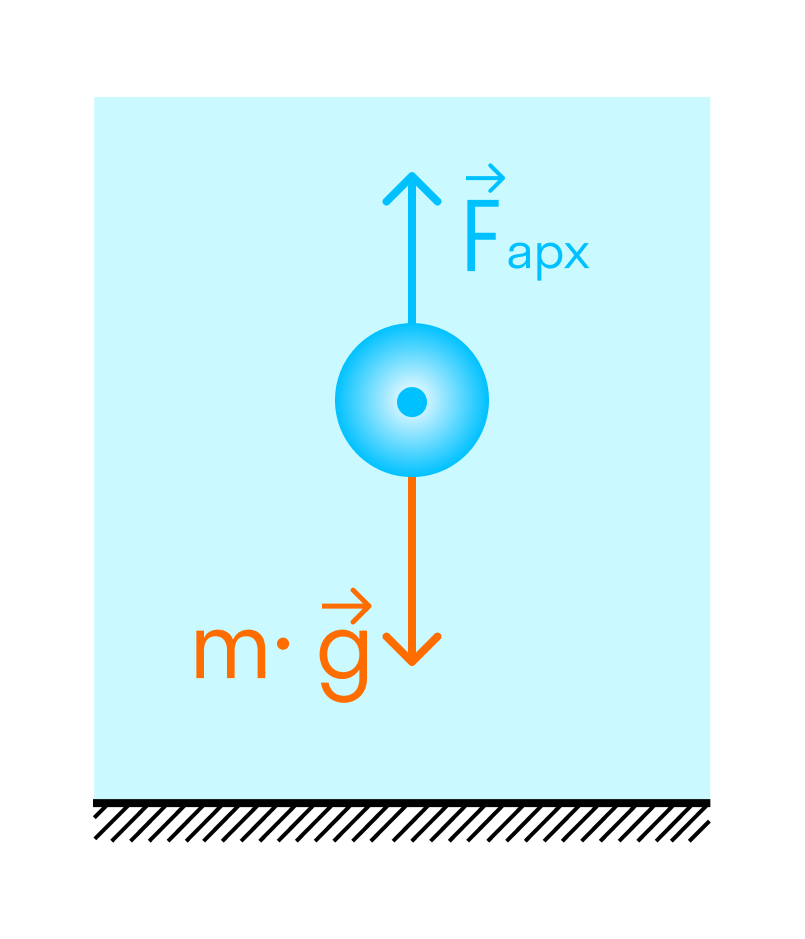
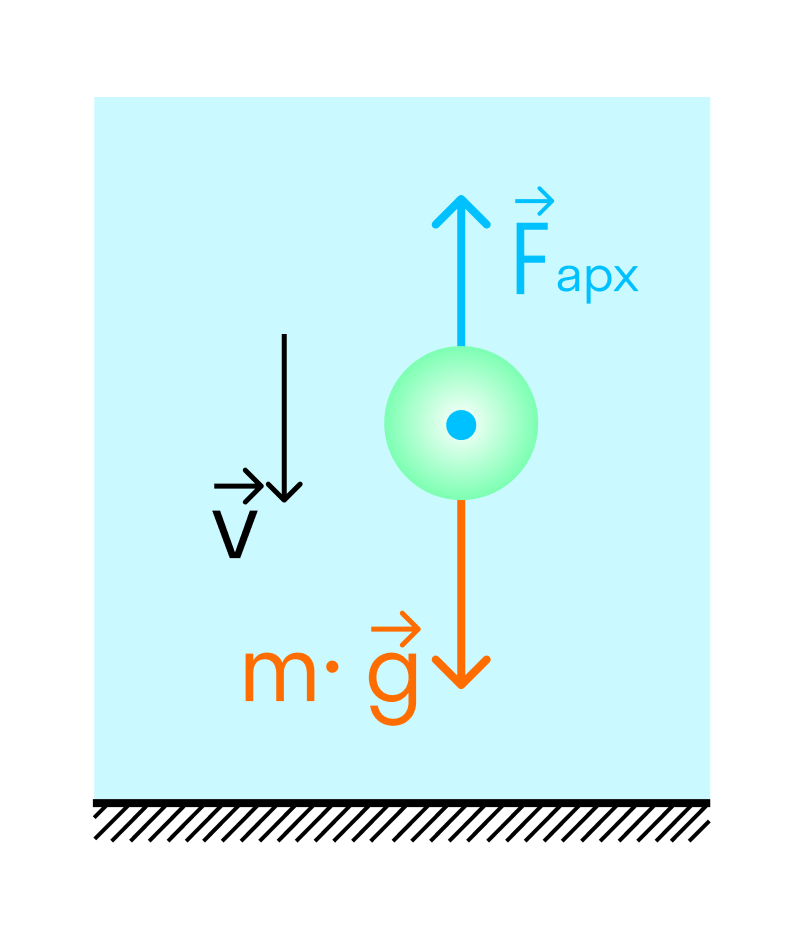
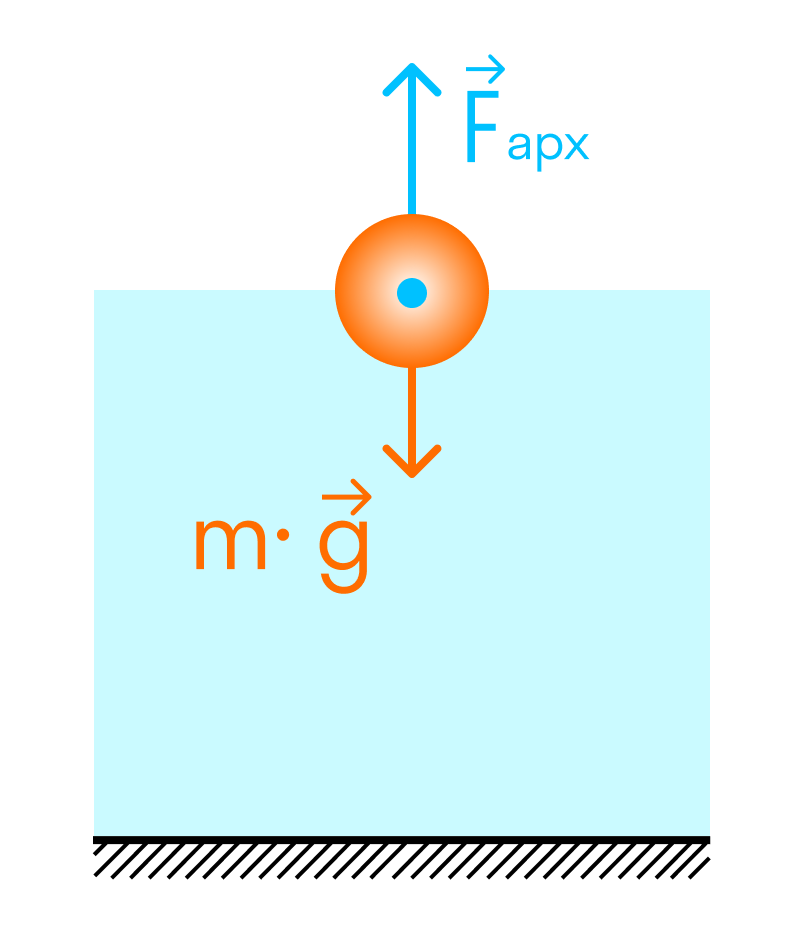
Если плотность тела меньше плотности жидкости или газа — оно будет плавать на поверхности.
Почему корабли не тонут?
Корабль сделан из металла, плотность которого больше плотности воды. И, по идее, он должен тонуть. Но дело в том, что корпус корабля заполнен воздухом, поэтому общая плотность судна оказывается меньше плотности воды, и сила Архимеда выталкивает его на поверхность. Если корабль получит пробоину, то пространство внутри заполнится водой — следовательно, общая плотность корабля увеличится. Судно утонет.
В подводных лодках есть специальные резервуары, которые заполняют водой или сжатым воздухом. Если нужно уйти на глубину — водой, если подняться — сжатым воздухом. Рыбы используют такой же принцип в плавательном пузыре — наполняют его воздухом, чтобы подняться наверх.
Человеку, чтобы не утонуть, тоже достаточно набрать в легкие воздух и не двигаться — вода будет выталкивать тело на поверхность. Именно поэтому важно не тратить силы и кислород в легких на панику и борьбу, а расслабиться и позволить физическим законам сделать все за нас.
Формула и определение силы Архимеда для газов
На самом деле тут все очень похоже на жидкости. Начнем с формулировки закона Архимеда:
Выталкивающая сила, действующая на тело, погруженное в газ, равна по модулю весу вытесненного газа и противоположно ему направлена.
Формула архимедовой силы для газов
ρг — плотность газа [кг/м 3 ]
Vпогр — объем погруженной части тела [м 3 ]
g — ускорение свободного падения [м/с 2 ]
Сила Архимеда для газов действует аналогично архимедовой силе для жидкостей. Давайте убедимся в этом, решив задачку.
Задача
Решение
Подставляем значения и получаем:
По второму закону Ньютона для инерциальных систем отсчета:
Выражаем массу груза и подставляем значения:
m = FАрх / g = 0,39 / 10 = 0, 039 кг = 39 кг
Ответ: груз максимальной массы 39 г может удержать данный шарик с гелием.
Когда сила Архимеда не работает
Архимедова сила не работает лишь в трех случаях:
Невесомость. Главное условие возникновения Архимедовой силы — это наличие веса у среды. Если мы находимся в невесомости, холодный воздух не опускается, а горячий, наоборот, не поднимается.
Тело плотно прилегает к поверхности. Отсутствие газа или жидкости между поверхностью и телом свидетельствует об отсутствии выталкивающей силы — телу просто неоткуда выталкиваться.
Растворы и смеси. Если взять спирт, плотность которого меньше плотности воды, и смешать его с водой, получится раствор. На него не будет действовать сила Архимеда, несмотря на то, что плотность спирта меньше плотности воды — он просто растворится.
Объемы фигур. Объем параллелепипеда.
Объем прямоугольного параллелепипеда, формула.
Параллелепипедом является призма, основание у которой – это параллелограмм. У параллелепипеда
6 граней, а они, в свою очередь, являются параллелограммами.
Прямой параллелепипед, у которого все 6 граней прямоугольники, является прямоугольным.
Другими словами, прямоугольный параллелепипед — это объемная фигура, у которой есть 6 граней, и
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:
a – длина параллелепипеда,
b – ширина параллелепипеда,

Примеры прямоугольного параллелепипеда: спортивный зал, кирпич, картонная коробка или столешница
Длины 3 рёбер прямоугольного параллелепипеда, которые имеют общий конец, называются измерениями
прямоугольного параллелепипеда.
Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба — это
Квадрат длины диагонали прямоугольного параллелепипеда = сумме квадратов 3 его измерений.
Объем прямого параллелепипеда, формула.
Как найти объем параллелепипеда?
Площадь боковой поверхности параллелепипеда, формула:
где Ро — периметр основания,
Площадь полной поверхности, формула
где Sо — площадь основания
Формула объёма прямого параллелепипеда:
Объем произвольного параллелепипеда.
Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры.
Чему равен объём параллелепипеда? Объем параллелепипеда равен абсолютной величине смешанного
произведения трёх векторов, которые определяются 3-мя сторонами параллелепипеда, которые исходят
Соотношение длина сторон параллелепипеда – угол между ними даёт утверждение, что определитель
Грама указанных 3х векторов равен квадрату их смешанного произведения.
Объем конуса
Объём конуса выражается такой же формулой, что и объём пирамиды: V = 1 /3 Sh,
где V — объём конуса, S — площадь основания конуса, h — его высота.
Окончательно V = 1 /3 πR 2 h, где R — радиус основания конуса.
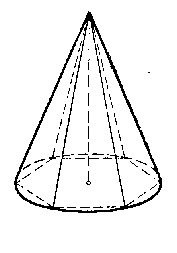
Получение формулы объёма конуса можно пояснить таким рассуждением:
Пусть дан конус (рис). Впишем в него правильную пирамиду, т. е. построим внутри конуса такую пирамиду, вершина которой совпадает с вершиной конуса, а основанием служит правильный многоугольник, вписанный в основание конуса.
Объём этой пирамиды выразится формулой: V’ = 1 /3 S’h, где V — объём пирамиды,
S’ — площадь её основания, h — высота пирамиды.
Если при этом за основание пирамиды взять многоугольник с очень большим числом сторон, то площадь основания пирамиды будет весьма мало отличаться от площади круга, а объём пирамиды — весьма мало отличаться от объёма конуса. Если, пренебречь этими различиями в размерах, то объём конуса выразится следующей формулой:
V = 1 /3 Sh, где V — объём конуса, S — площадь основания конуса, h — высота конуса.
Примечание. В формуле V = 1 /3 Sh поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы его считать приближённым, но в старших классах средней школы доказывается, что равенство
V = 1 /3 Sh точное, а не приближённое.
Объем произвольного конуса
Теорема. Объем произвольного конуса равен одной трети произведения площади основания на высоту, т.е.
где Q — площадь основания, а Н — высота конуса.
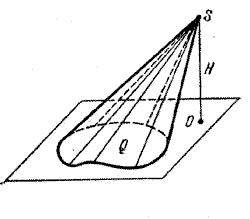
Рассмотрим конус с вершиной S и основанием Ф (рис.).
Пусть площадь основания Ф равна Q, а высота конуса равна Н. Тогда существуют последовательности многоугольников Фn и Ф’n с площадями Qn и Q’n таких, что
Очевидно, что пирамида с вершиной S и основанием Ф’n будет вписанной в данный конус, а пирамида с вершиной S и основанием Фn — описанной около конуса.
Объемы этих пирамид соответственно равны
то формула (1) доказана.
Следствие. Объем конуса, основанием которого является эллипс с полуосями а и b, вычисляется по формуле
В частности, объем конуса, основанием которого является круг радиуса R, вычисляется по формуле
где Н — высота конуса.
Как известно, площадь эллипса с полуосями а и b равна π ab, и поэтому формула (2) получается из (1) при Q = π ab. Если а = b = R, то получается формула (3).
Объем прямого кругового конуса
Теорема 1. Объем прямого кругового конуса с высотой Н и радиусом основания R вычисляется по формуле
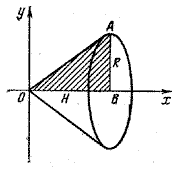
Данный конус можно рассматривать как тело, полученное вращением треугольника с вершинами в точках О(0; 0),В(Н; 0), А(Н; R) вокруг оси Ох (рис.).
Треугольник ОАВ является криволинейной трапецией, соответствующей функции
у = R /H х, х ∈ [0; H]. Поэтому, используя известную формулу, получаем
Следствие. Объем прямого кругового конуса равен одной трети произведения площади основания на высоту, т. е.
где Q — площадь основания, а H — высота конуса.
Теорема 2. Объем усеченного конуса с радиусами оснований r и R и высотой H вычисляется по формуле
Усеченный конус можно получить вращением вокруг оси Ох трапеции О ABC (рис.).
Прямая АВ проходит через точки (0; r) и (H; R), поэтому она имеет уравнение
Для вычисления интеграла сделаем замену
Очевидно, когда х изменяется в пределах от 0 до H, переменная и изменяется от r до R, и поэтому
Формула объема.
Формула объема необходима для вычисления параметров и характеристик геометрической фигуры.