В чем заключается графический способ описания движения кратко

ГЛАВА 6. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ

Рисунок – источник и душа каждого
изображения и корень каждой науки.
Микеланджело

Для описания движения тела часто используется графический язык, когда на некоторой координатной плоскости строятся графики зависимости одного кинематического параметра от другого. Наиболее часто используются графики зависимости координаты, скорости или ускорения тела от времени, хотя возможны и другие варианты, например, зависимость одной координаты тела от другой, или скорости от координаты и т.д. Такой способ описания является достаточно удобным и плодотворным, поскольку позволяет как «увидеть» все движение в целом, так и выделить его наиболее характерные особенности.

Рассмотрим несколько примеров, в которых содержатся основные принципы построения графиков движений или извлечения из этих графиков той или иной информации о движении тела.

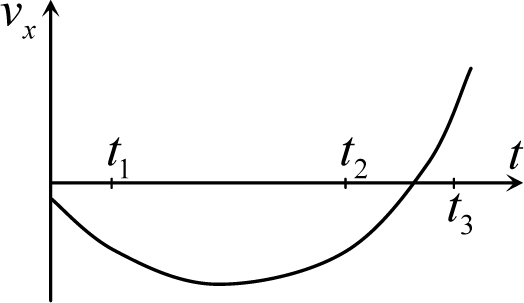
Пример 6.1. Тело движется прямолинейно вдоль некоторой оси x . На рис. 6.1 приведен график зависимости проекции скорости тела на ось x от времени. Сравнить проекции ускорения тела на ось x в моменты времени t ₁ , t ₂ и t ₃ . Доказать, что на графике v_x ( t ) не может быть разрывов.

Решение. Основная идея ответа на поставленный вопрос заключается в том, что мгновенному ускорению тела соответсвуют геометрические характеристики рассматриваемого графика. Для установления этого соответствия будем исходить из определения мгновенного ускорения в некоторый момент времени t :

Источник

В чем заключается графический способ описания движения кратко

В кинематике существуют три способа аналитического описания движения материальной точки в пространстве. Рассмотрим их, ограничившись случаем движения материальной точки на плоскости, что позволит нам при выборе системы отсчёта задавать лишь две координатные оси.

1. Векторный способ.

В этом способе положение материальной точки `A` задаётся с помощью так называемого радиус-вектора `vecr`, который представляет собой вектор, проведённый из точки `O`, соответствующей началу отсчёта выбранной системы координат, в интересующую нас точку `A` (рис. 1). В процессе движения материальной точки её радиус-вектор может изменяться как по модулю, так и по направлению, являясь функцией времени `vecr=vecr(t)`.

Геометрическое место концов радиус-вектора `vecr(t)` называют траекторией точки `A`.

В известном смысле траектория движения представляет собой след (явный или воображаемый), который «оставляет за собой» точка `A` после прохождения той или иной области пространства. Понятно, что геометрическая форма траектории зависит от выбора системы отсчёта, относительно которой ведётся наблюдение за движением точки.

Пусть в процессе движения по некоторой траектории в выбранной системе отсчёта за промежуток времени `Delta t` тело (точка `A`) переместилось из начального положения `1` с радиус-вектором `vec r_1` в конечное положение `2` с радиус-вектором `vec r_2` (рис. 2). Приращение `Deltavec r` радиус-вектора тела в таком случае равно: `Deltavec r = vec r_2- vec r_1`.

Вектор `Deltavec r`, соединяющий начальное и конечное положения тела, называют перемещением тела.

Отношение `Delta vec r//Delta t` называют средней скоростью (средним вектором скорости) `vec v_»cp»` тела за время `Delta t`:

`vecv_»cp»=(Deltavecr)/(Delta t)` (1)

Вектор `vecv_»cp»` коллинеарен и сонаправлен с вектором `Deltavec r`, так как отличается от последнего лишь скалярным неотрицательным множителем `1//Delta t`.

Предложенное определение средней скорости справедливо для любых значений `Delta t`, кроме `Delta t=0`. Однако ничто не мешает брать промежуток времени `Delta t` сколь угодно малым, но отличным от нуля.
Для точного описания движения вводят понятие мгновенной скорости, то есть скорости в конкретный момент времени `t` или в конкретной точке траектории. С этой целью промежуток времени `Delta t` устремляют к нулю. Вместе с ним будет стремиться к нулю и перемещение `Delta vec r`. При этом отношение `Deltavec r//Delta t` стремится к определённому значению, не зависящему от `Delta t`.

Величина, к которой стремится отношение `Deltavec r//Delta t` при стремлении `Delta t` к нулю, называется мгновенной скоростью`vec v`:

Теперь заметим, что чем меньше `Delta t`, тем ближе направление `Deltavec r` к направлению касательной к траектории в данной точке. Следовательно, вектор мгновенной скорости направлен по касательной к траектории в данной точке в сторону движения тела.

В дальнейшем там, где это не повлечёт недоразумений, мы будем опускать прилагательное «мгновенная» и говорить просто о скорости `vec v` тела (материальной точки).

Движение тела принято характеризовать также ускорением, по которому судят об изменении скорости в процессе движения. Его определяют через отношение приращения вектора скорости `Delta vec v` тела к промежутку времени `Delta t`, в течение которого это приращение произошло.

Ускорением `veca` тела называется величина, к которой стремится отношение `Delta vec v//Delta t` при стремлении к нулю знаменателя `Delta t`:

При уменьшении `Delta t` ориентация вектора`Delta vec v` будет приближаться к определённому направлению, которое принимается за направление вектора ускорения `vec a`. Заметим, что ускорение направлено в сторону малого приращения скорости, а не в сторону самой скорости!

Напомним, что в системе СИ единицами длины, скорости и ускорения являются соответственно метр (м), метр в секунду (`»м»//»с»`) и метр на секунду в квадрате ( `»м»//»с»^2`).

2. Координатный способ.

3. Естественный (или траекторный) способ.

Этот способ применяют тогда, когда траектория материальной точки известна заранее. На заданной траектории `LM` (рис. 5) выбирают начало отсчёта – неподвижную точку `O`, а положение движущейся материальной точки `A` определяют при помощи так называемой дуговой координаты `l`, которая представляет собой расстояние вдоль траектории от выбранного начала отсчёта `O` до точки `A`. При этом положительное направление отсчёта координаты `l` выбирают произвольно, по соображениям удобства, например так, как показано стрелкой на рис. 5.

Ясно, что пройденный путь – величина скалярная и неотрицательная, а потому его нельзя сравнивать с перемещением `Delta vec r`, представляющим собой вектор. Сравнивать можно только путь `Delta S` и модуль перемещения `
|Delta vecr|`. Очевидно, что `Delta S >=|Deltavec r|`.

Средней путевой скоростью `v_»cp»` тела называют отношение пути `Delta S` к промежутку времени `Delta t`, в течение которого этот путь был пройден:

`v_»cp»=(Delta S)/(Delta t)` (3)

Определённая ранее средняя скорость `v_»cp»` (см. формулу (1)) и средняя путевая скорость отличаются друг от друга так же, как `Deltavec r` отличается от `Delta S`, но при этом важно понимать, что обе средние скорости имеют смысл только тогда, когда указан промежуток времени усреднения `Delta t`. Само слово «средняя» означает усреднение по времени.

Городской троллейбус утром вышел на маршрут, а через 8часов, проехав в общей сложности `72` км, возвратился в парк и занял своё обычное место на стоянке. Какова средняя скорость `vec v_»cp»` и средняя путевая скорость `v_»cp»` троллейбуса?

Поскольку начальное и конечное положения троллейбуса совпадают, то его перемещение `Delta vecr` равно нулю: `Deltavecr=0`, следовательно, `vecv_»ср»=Deltavecr//Deltat=0` и `|vecv_»ср»|=0`. Но средняя путевая скорость троллейбуса не равна нулю:

`v_»cp»=(Delta S)/(Delta t)=(72 «км»)/(8 «ч»)=9 «км»//»ч»`.

Источник

12-к. Графическое описание движений

§ 12-к. Графическое описание движений

В самом начале изучения кинематики мы отметили, что движение тел можно описывать графически, и привели пример графика зависимости пути от времени (см. § 12-а). Теперь мы знаем, что движение тел характеризуется и другими величинами: перемещением, скоростью, ускорением. Они тоже могут быть отражены на графиках.

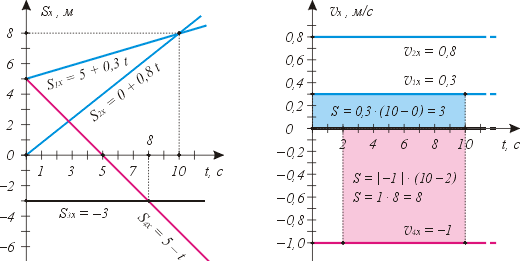
Графики для прямолинейного равномерного движения:

Слева – графики зависимости от времени проекций перемещений четырёх разных тел, движущихся с различными скоростями. Медленнее всех вдоль оси Х движется первое тело: его скорость 0,3 м/с сонаправлена оси X. Быстрее всех движется четвёртое тело: его скорость 1 м/с противонаправлена оси Х (на что указывает отрицательное значение проекции). Точка пересечения графиков в момент времени 10 с означает, что тела 1 и 2 имели равные проекции перемещений: 8 м. Аналогично, тела 3 и 4 в момент времени 8 с тоже имели равные проекции перемещений: по –3 м. А что вы скажете про 2 и 4 тела?

Справа – графики зависимости от времени проекций скоростей этих тел (на прежнюю ось). Все четыре линии показывают, что все проекции скоростей с течением времени не меняются. А что иллюстрируют цветные прямоугольники? – вероятно, спросите вы.

Обратим внимание: площадь прямоугольника, заключённого между линией графика проекции скорости, осью абсцисс и двумя выбранными ординатами, численно равна пути, пройденному телом за интервал времени между выбранными моментами. Например, площадь под первым графиком за интервал времени с 0 до 10 с численно равна трём. Взглянув на первый график слева, мы видим: проекция перемещения изменилась с 5 до 8 м, то есть на 3 м за то же время.

Графики для прямолинейного равноускоренного движения не для всех величин являются прямолинейными (см. выше). С чем это связано?

Как вы узнали в § 12-й, при равноускоренном движении проекции перемещения зависят от времени по квадратичному закону. Графически это выражается частями парабол (см. левую часть чертежа, внизу). Наряду с этим в § 12-и вы узнали, что при равноускоренном движении проекции мгновенной скорости зависят от времени по линейному закону. Графически это выражается прямыми линиями (см. среднюю часть чертежа, которую мы построили по значениям из левой части). Справа показано, что проекции ускорений тех же тел не изменяются с течением времени, так как их движения равноускоренные.

С точки зрения физики, графики зависимостей кинематических величин от времени несут ту же информацию, что и алгебраические формулы. Поэтому вы можете использовать алгебраический и графический способы как равноправные.

Источник

Механическое движение

Механическое движение

Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.

Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.

«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:

В совокупности эти три параметра образуют систему отсчета.

В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

Векторные величины (определяются значением и направлением)

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.

Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость

→ →
V = S/t

→
V — скорость [м/с]
→
S — перемещение [м]
t — время [с]

Средняя путевая скорость

V ср.путевая = S/t

V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости
V ср.путевая = S/t

Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уравнение движения

Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения

x(t) = x0 + vxt

x(t) — искомая координата [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

Уравнение движения при движении против оси

x(t) — искомая координата [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Графики

Изменение любой величины можно описать графически. Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.

В видео ниже разбираемся, как строить графики кинематических величин и зачем они нужны.

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения

x(t) = x0 + v0xt + axt^2/2

x(t) — искомая координата [м]
x0 — начальная координата [м]
v0x — начальная скорость тела в данный момент времени [м/с]
t — время [с]
ax — ускорение [м/с^2]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости

→ →
v = v0 + at

→
v — конечная скорость тела [м/с]
v0 — начальная скорость тела [м/с]
t — время [с]
→
a — ускорение [м/с^2]

Задача

Найдите местоположение автобуса через 0,5 часа после начала движения, разогнавшегося до скорости 60 км/ч за 3 минуты.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, v0 = 0. Значит
a = v/t

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч^2
Теперь возьмем уравнение движения.
x(t) = x0 + v0xt + axt^2/2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
x = 1200*0,5^2/2 = 1200*0,522= 150 км

Ответ: через полчаса координата автобуса будет равна 150 км.

Графики

Мы уже знаем, что такое графики функций и зачем они нужны. Для прямолинейного равноускоренного движения графики будут отличаться. Об этом — в видео ниже

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с^2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Источник

В чем заключается графический способ описания движения кратко

Какими величинами можно описать механическое движение тела?

Если тело можно считать точкой, то для описания его движения нужно научиться рассчитывать положение точки в любой момент времени относительно выбранного тела отсчёта.

Существует несколько способов описания, или, что одно и то же, задания движения точки. Рассмотрим два из них, которые наиболее часто применяются.

Координатный способ.

Будем задавать положение точки с помощью координат. Если точка движется, то её координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями времени.

Математически это принято записывать в виде

Уравнения (1.1) называют кинематическими уравнениями движения точки, записанными в координатной форме.

Если уравнения движения известны, то для каждого момента времени мы сможем рассчитать координаты точки, а следовательно, и её положение относительно выбранного тела отсчёта. Вид уравнений для каждого конкретного движения будет вполне определённым.

Основной задачей кинематики является определение уравнения движения тел.

Количество выбираемых для описания движения координат зависит от условий задачи. Если движение точки происходит вдоль прямой, то достаточно одной координаты и, следовательно, одного уравнения, например, x(t). Если движение происходит на плоскости, то его можно описать двумя уравнениями — x(t) и y(t). Уравнения описывают движение точки в пространстве.

Векторный способ.

Положение точки можно задать, и с помощью радиус-вектора.

Радиус-вектор — это направленный отрезок, проведённый из начала координат в данную точку.

При движении материальной точки радиус-вектор, определяющий её положение, с течением времени изменяется (поворачивается и меняет длину), т. е. является функцией времени:

= (t)

На рисунке радиус-вектор определяет положение точки в момент времени t₁, а радиус-вектор ₂ — в момент времени t₂.

Вышеприведенная формула и есть уравнение движения точки, записанное в векторной форме.

Если оно известно, то мы можем для любого момента времени рассчитать радиус-вектор точки, а значит, определить её положение.

Задание трёх скалярных уравнений равносильно заданию одного векторного уравнения.

Итак, мы знаем, что положение точки в пространстве определяется её координатами или её радиус-вектором.

Модуль и направление любого вектора находят по его проекциям на оси координат. Чтобы понять, как это делается, вначале необходимо ответить на вопрос: что понимают под проекцией вектора на ось?

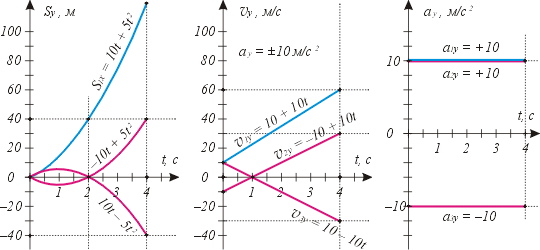
Изобразим ось ОХ. Опустим из начала А и конца В вектора перпендикуляры на ось ОХ. Точки А₁ и В₁ есть проекции соответственно начала и конца вектора на эту ось.

Проекция вектора

Проекцией вектора на какую-либо ось называется длина отрезка А₁В₁ между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «—».

Проекцию вектора мы будем обозначать той же буквой, что и вектор, но, во-первых, без стрелки над ней и, во-вторых, с индексом внизу, указывающим, на какую ось проецируется вектор. Так, а_х и а_у — проекции вектора на оси координат ОХ и OY.

Согласно определению проекции вектора на ось можно записать:

Проекция вектора на ось представляет собой алгебраическую величину. Она выражается в тех же единицах, что и модуль вектора.

Условимся считать проекцию вектора на ось положительной, если от проекции начала вектора к проекции его конца надо идти в положительном направлении оси проекций.
В противном случае она считается отрицательной.

Проекция вектора на ось будет положительной, когда вектор составляет острый угол φ с направлением оси проекций, и отрицательной, когда вектор составляет с направлением оси проекции тупой угол φ.

Иногда нужно находить составляющие вектора, например векторы _x, и _y.

Сумма составляющих равна вектору :

= _x + _y.

Источник

• ← Как зафиксировать изображение в компасе
• Как класть тротуарную плитку на пескобетон →