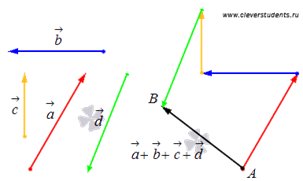
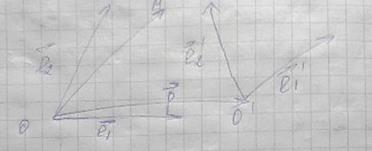
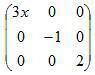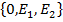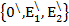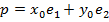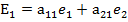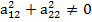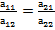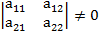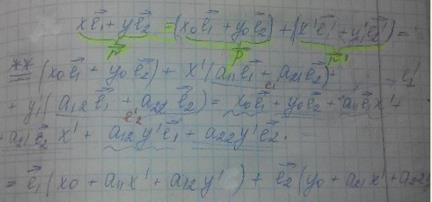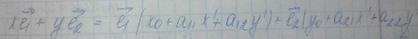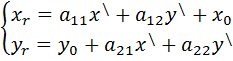В чем заключается правило многоугольника сложения двух нескольких векторов

Операции над векторами и их свойства: сложение и умножение

Прежде чем приступить к тематике статьи, напомним основные понятия.

Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.

Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.

Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.

Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.

Сложение двух векторов

Геометрически сложение векторов выглядит так:

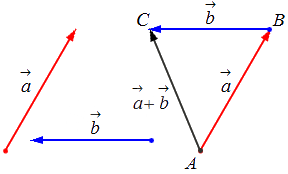
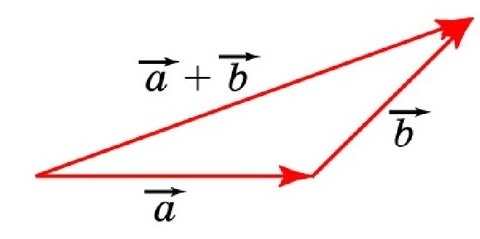
— для неколлинеарных векторов:

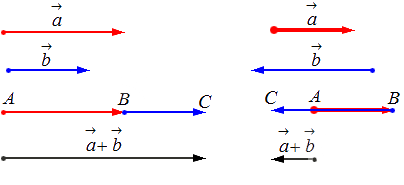
— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:

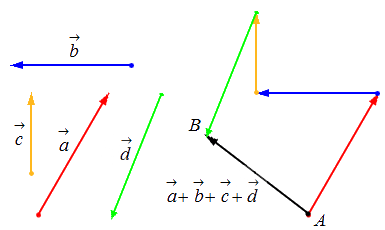
Сложение нескольких векторов

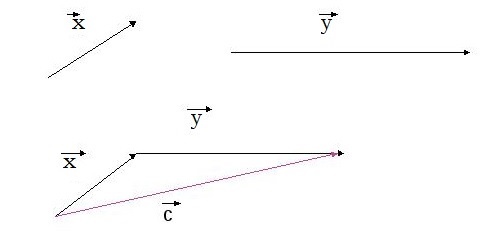
Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.

Геометрически оно выглядит следующим образом:

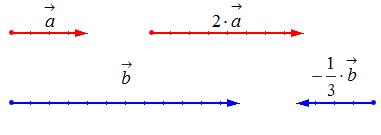
Умножение вектора на число

Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:

Свойства операций над векторами

Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.

Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.

Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.

Источник

Сложение и вычитание векторов – правила

Сложение и вычитание векторов – это одно из немногих действий на стыке математики и геометрии. Дело в том, что выражения из векторов можно складывать и вычитать арифметически, ориентируясь только по буквенным обозначениям отрезков, но для того, чтобы получить числовой результат или его геометрическое отображение придется выполнить ряд построений. Разберемся подробнее в правилах сложения и вычитания векторов.

Что такое вектор?

Вектор это образок с направлением.

Вектор и луч часто путают и допускают грубую ошибку. Вектор то направленный отрезок, а любой отрезок имеет величину, то есть его можно измерить линейкой. Луч имеет начало и направление, но он бесконечен, то есть измерить его невозможно. Так же, как нельзя и складывать лучи между собой или луч с вектором.

Вектор иногда помещают в декартову систему координат. Тогда проведя перпендикуляры к каждой из осей, можно получить проекции вектора на оси х и у. Каждая из этих проекций будет отрезком. При этом, если из проекций составить прямоугольник, то его гипотенуза и будет начальным вектором. Это иногда используется при сложении векторов.

Рис. 1. Вектор в системе координат.

Сложение и вычитание векторов

Способов и методов сложения векторов всего два. Существует и третий, но его не считают отдельным методом, так как он проистекает из первых двух. Но мы его рассмотрим отдельно, чтобы не возникало вопросов при дальнейшем изучении темы.

Правило многоугольника

Для того, чтобы сложить вектора правилом многоугольника, необходимо параллельным переносом совместить конец первого вектора с началом второго, конец второго с началом третьего и так далее, пока не кончатся вектора, которые необходимо складывать.

После этого нужно конец последнего вектора соединить с началом первого и указать направление. Получившийся вектор будет направлен в сторону последнего из учавствовавших в сложении.

Складывать таким способом можно любое количество векторов. Если так складывается только два вектора, то способ называют правилом треугольника

Нужно понять и запомнить, что у отрезка одна определяющая величина: размер. У вектора определяющих величин две: размер и направление. Поэтому нельзя менять направление вектора и его размер. Любые действия нужно осуществлять с помощью параллельного переноса, то есть без изменения направления.

Рис. 2. Правило многоугольника.

Правило параллелограмма

Правило параллелограмма сложнее, его можно применять только для 2 векторов. Если вам нужно этим способом сложить большее количество векторов, например, три, то действие выполняют в следующем порядке:

Само правило параллелограмма заключается в том, что начала двух векторов совмещаются. После этого получившуюся фигуру достраивают до параллелограмма. Диагональ, которая выходит из начала двух векторов и есть результат сложения. Вектор должен быть направлен в противоположную сторону от совмещенного начала двух векторов.

Для того чтобы вычесть вектора любым способом, направление вектора, который является вычитаемым, меняют на противоположное. Получившиеся вектора складывают любым из методов.

Рис. 3. Правило прямоугольника.

Сложение в декартовой системе

В декартовой системе все вектора раскладывают на проекции, после чего отрезки проекций складывают: проекции на ось х отдельно, на ось у отдельно. После из получившихся двух проекций снова собирают вектор.

Что мы узнали?

Мы узнали, что такое вектор. Поговорили о правилах сложении и вычитании векторов. Обсудили, чем отличается вектор от луча и обсудили метод действий с векторами в декартовой системе координат.

Источник

Сложение векторов — свойства, правила и примеры решения задач

Отрезок, который имеет направление, называется вектором. По сути, эта линия, характеризующаяся определённой длиной. Так как с математической точки зрения это выражение, то с ним можно выполнять различные операции. Простейшими являются действия вычитания двух и более векторов и их сложение. Выполняются они по правилам геометрии и алгебры.

Общие сведения

Понятие вектор используется как в физике, так и в математике. С его помощью обозначают действие различных сил, указывают их направление, определяют движение. По сути, это величина, противопоставляемая массе, объёму, плотности, температуре, то есть «скалярам». Согласно определению вектор — это отрезок, имеющий строгое направление. Точку, из которой он выходит, называют начальной, а в которой заканчивается — конечной.

Обозначают отрезок помощью заглавных латинских букв, сверху которых ставится чёрточка. Рисуют же его с помощью прямой ограниченной линии.

Например, запись AB обозначает, что точка A является началом, а B концом. В некоторых случаях для кратности отрезки допустимо обозначать одной маленькой буквой, так: AB = a.

Векторная запись используется тогда, когда невозможно величины описать с помощью одного числа. Численное значение выражение определяется длиной отрезка или его модулем. Эта величина является скалярной. В том случае если начало и конец ограниченной линии совпадают, то говорят о нулевой линии. Обозначают её цифрой 0.

Векторы, расположенные на плоскости или в пространстве, по отношению друг к другу могут быть:

Так как вектора — это выражения, то с ними можно выполнять различные действия. Их возможно складывать, вычитать, умножать на число. При работе с векторными величинами используют декартовую систему координат. В ней прямую замкнутую линию раскладывают по базису и определяют координаты её точек. Другими словами, выполняют проекции отрезков на оси. Непосредственно за базис берут орты.

Если известны начальные координаты и конечные, то текущие вычисляют путём вычитания из последних первые. Существующая возможность записать любое геометрическое свойство, используя координаты, позволяет отойти от геометрии и использовать для вычислений алгебру.

Сложение координат

Существует простое правило применимое для направленных отрезков и позволяющее найти их сумму. Заключается оно в следующем: если необходимо прибавить один вектор к другому описывающийся каждый своими координатами, достаточно сложить соответствующие их орты. Например, предположим есть два вектора a и b. Первый отрезок имеет координаты (ax; ay), а второй (bx;by). При их сложении получится новый вектор c. В результате действия его координаты будут c (ax + bx; ay + by).

Это теорема доказывается просто. Пусть даны отрезки f (x 1; y 1) и g (x 2; y 2). В системе координат относительно рассматриваемых векторов получится: f = x 1 a + y 1 b; g = x 2 a + y 2 b. Тогда искомая сумма будет: f + g = x1a + y1b + x2a + y2b = a (x 1 + x 2) + b (y 1 + y 2). Что и нужно было доказать. Это правило применимо к векторам имеющим любые координаты. Например, пусть есть a (1; 2), b (-3; 1). Нужно найти их сумму. С помощью формулы сложения получится новый направленный отрезок с координатами a + b = (1 — 3; 2 + 1) = (-2; 3).

Как и при операциях с простыми числами при работе с векторными выражениями используют различные их свойства. Существует три правила сложения векторов:

Следует отметить, что при сложении двух противоположных ограниченных прямых сумма будет равняться нуль-вектору: a + (-a) = 0. Это утверждение не требует доказательства, так как здесь используется фундаментальный закон алгебры — правило знаков.

Правило параллелограмма

По сути, все операции с векторными выражениями сводятся к их приращению или уменьшению. Если координаты точек неизвестны, то алгебраический метод складывания не подходит. В таком случае используют геометрические операции. Одним из способов, позволяющих сложить два неколлинеарных вектора, является правило параллелограмма или прямоугольника при перпендикулярном направлении складываемых отрезков.

Сформулировать способ можно следующим образом: если имеются два отрезка не лежащие на параллельной прямой и не принадлежащие ей, то нужно достроить данные вектора до параллелограмма. Для этого необходимо взять произвольную точку и отложить от неё отрезок AB равный первому вектору, и AD совпадающий со вторым. При этом необходимо придерживаться соотношения геометрии наклона. Затем достроить необходимые параллельные прямые таким образом, чтобы образовался параллелограмм ABCD. Если в такой фигуре провести диагональ, то её длина и будет равняться сумме складываемых отрезков.

Доказать правильность утверждения можно следующими доводами. Пусть имеются две ограниченные линии a и b. От точки A можно отложить первый отрезок конец, которого обозначить как B, и второй, с точкой D. Теперь через D и B возможно провести соответственно параллельные прямые AB и AD. Место, в которой они пересекутся, пусть будет обозначено как С. Тогда используя признак параллельности двух пар прямых в фигуре ABCD, можно утверждать, что это параллелограмм. Вектор AC = a + b. Это следует из равенства отрезков AD = BC и теоремы о подобных треугольниках.

Пример задания. Определить, чему равна сумма двух отрезков длиной 2 см и 1 см расположенные друг к другу под углом 45. Для того чтобы воспользоваться правилом, нужно взять листочек в клеточку и построить два вектора, исходящие из одной точки O. Тогда первый отрезок будет OA, а второй OB. Затем достроить прямые таким образом, чтобы на рисунке получился параллелограмм. Новая полученная точка пусть будет D. Теперь с помощью линейки можно измерить диагональ фигуры, длина которой и будет искомой суммой. В ответе должно получиться, что OA + OB = OD = 3 см.

Простыми словами это правило можно рассказать так: сумма двух отрезков будет равняться диагонали параллелограмма, построенного на исходных векторах. Эта теорема чаще используется не в геометрии, а физике, например, при сложении сил.

Альтернативные методы

Операцию по сложению двух векторов можно выполнить и с помощью правила треугольника. Делается это так. Выбирается любая точка на плоскости, от которой откладываются два вектора. При этом необходимо соблюдать их размерность и наклон по отношению друг к другу. Затем две конечные точки соединяют прямой. Её длина и будет искомой величиной. То есть в итоге должна получиться равнобедренная фигура.

Применение метода сложения векторов по правилу треугольника позволяет довольно легко находить сумму для трёх и более отрезков. Для этого сначала вычисляют результат сложения для двух любых линий, а после прибавляют к полученной ограниченной прямой третью и так далее.

При сложении нескольких векторов удобно выполнять следующую последовательность построений:

Этот способ получил название метод многоугольника. Он довольно часто применяется на практике, позволяя, довольно просто выполнить нахождение суммы. Из правила треугольника, а, следовательно, и многоугольника, вытекает следствие, которое подтверждает, что если складывается отрезок с нулевым векторным выражением, то в ответе получится длина, совпадающая со значимым слагаемым.

Следует отметить, что методы используются только, если направление отрезков является сонаправленным.

Если же отрезки неколлинеарные, то от конца одного откладывается другой. Тогда искомая сумма будет равняться длине линии, первой точкой которой будет начало одной векторной прямой, а конец совпадать с точкой, завершающей другую. То есть сумма — это отрезок, начало которого совпадает с началом обеих линий, а длина равна разности их длин, при этом направление его будет совпадать с тем что больше по длине.

Источник

К коллинеарным векторам это построение неприменимо.

Основываясь на рассмотренной операции сложения двух векторов, мы можем сложить три вектора и более. В этом случае складываются первые два вектора, к полученному результату прибавляется третий вектор, к получившемуся прибавляется четвертый и так далее.

Сложение нескольких векторов на плоскости таким способом называется правилом многоугольника. Приведем иллюстрацию правила многоугольника.

1.3. Умножение вектора на число k соответствует растяжению вектора в k раз при k > 1 или сжатию в 1/k раз при 0

Числа aij, входящие в состав данной матрицы, называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j — номер столбца.

Строка матрицы называется нулевой, если все ее элементы равны нулю.

Если хотя бы один из элементов строки матрицы не равен нулю, то строка называется ненулевой.

Столбец матрицы называется нулевым, если все его элементы равны нулю.

Если хотя бы один из элементов столбца матрицы не равен нулю, то столбец называется ненулевым.

2. Квадратной матрицейназывается матрица, у которой количество строк равно количеству столбцов (размера n×n), число n называется порядком матрицы.

	-7		— квадратная матрица размера 3×3
-1

Нулевой матрицейназывается матрица, все элементы которой равны нулю, т.е. aij = 0, ∀i, j.

— нулевая матрица

Вектор-строкой называется матрица, состоящая из одной строки.

-5

— вектор-строка

Вектор-столбцом называется матрица, состоящая из одного столбца.

		— вектор-столбец
-7

Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.

— не диагональные элементы равны нулю

Единичной матрицей называется диагональная матрица, диагональные элементы которой равны 1.

E =

— диагональные элементы равны 1

Верхней треугольной матрицей называется матрица, все элементы которой ниже главной диагонали равны нулю.

-6

Нижней треугольной матрицей называется матрица, все элементы которой выше главной диагонали равны нулю.

-2

Ступенчатой матрицей называется матрица, удовлетворяющая следующим условиям:

· если матрица содержит нулевую строку, то все строки, расположенные под нею, также нулевые;

· если первый ненулевой элемент некоторой строки расположен в столбце с номером i, и следующая строка не нулевая, то первый ненулевой элемент следующей строки должен находиться в столбце с номером большим, чем i.

-3

7. Преобразования координат на плоскости. Ориентация плоскости.

R=

Рассмотрим еще один R ̸̸ на той же плоскости R ̸̸ =

Рассмотрим вектор х на той же самой плоскости, возникает вопрос: как будут связаны между собой координаты этого вектора в 1 и во 2 базисе.

Полученные формулы будут называться формулами преобразования координат на плоскости.

Рассмотрим на плоскости точку М относительно старой системы координат, то это будут два числа (х,у)_R М=(х,у)_R

Связь между координатами R₁=xe₁+ye₂ и мы должны найти.

(1)

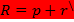
Если мы рассмотрим вектора нового базиса относительно старого базиса, то

(2)

Эти четыре числа (а₁₁, а₁₂, а₂₁, а₂₂) либо а_ig, где I,g=1,2 координаты базисных векторов из нового базиса.

А т.к. базисные вектора линейно независимые, значит каждый из них ненулевой вектор и они неколлинеарные, т.е. а₁₁ и а₂₁ ≠ 0 или 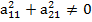(1 условие)

То что вектора не коллинеарные означает

Эти условия записываются в виде палочек а внутри типо таблица, это похоже на матрицу:

Таким образом мы получим

Эти формулы называются формулами преобразования координат на плоскости

Для прямоугольной декартовой системы координат эти формулы примут вид:

Источник

Сложение векторов в геометрии

Основные законы сложения векторов в геометрии

На плоскости найти сумму векторов можно, воспользовавшись формулой:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Если ситуация переходит в пространственное измерение, то достаточно всего лишь а тот же пример добавить новую координату:

Основные законы:

Помимо покоординатного сложения направленных отрезков, существуют геометрические нормы, которые позволяют узнать их сумму. Наиболее широко используемых методов в системе три: правило треугольника, параллелограмма и многоугольника.

Как происходит сложение по правилу треугольника

Чтобы узнать сумму векторов x и y, необходимо из произвольной точки отложить первый из них, а затем из его конца уже отложить второй. Следующий шаг — построить направленный отрезок, который соединит начало \vec x с концом \vec y. Образовавшаяся сторона треугольника и будет результатом сложения двух векторов. Теорема считается доказанной.

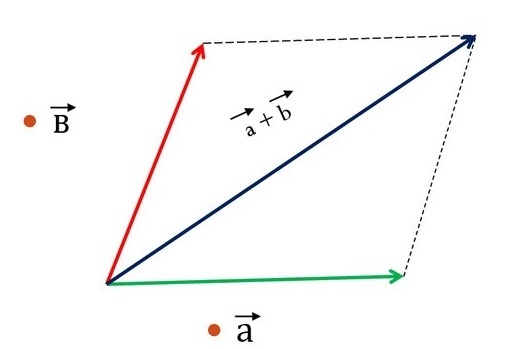
Сложение по правилу параллелограмма

Найти сумму векторов можно без построения треугольника. Для этого от начала первого вектора нужно отложить второй вектор. Дополним получившийся чертеж до параллелограмма. Две его стороны у нас уже имеются. Выстроить оставшиеся поможет способ параллельного переноса. Диагональ готовой фигуры, которая исходит из начальной точки векторов, считается их суммой. Теорема доказана.

Как и когда применяется правило многоугольника

Данный способ потребуется для того, чтобы сложить более двух векторов.

Принцип действий в данном случае похож на последовательность шагов, как в случае с треугольником. Из произвольной точки провести первый вектор. Из его конца — второй, из второго — третий и так далее. Затем окончание последнего вектора соединить с началом первого — это будет результат сложения всех векторов. Доказательство теоремы выполнено.

Задачи с примерами решения

Задача 1

Решение

Задача 2

С помощью правила треугольника постройте сумму заданных векторов a и b.

Решение 1

Решение 2

Одна цель достигнута разными способами, что наглядно демонстрирует действие переместительного закона.

Источник