В чем заключается преимущество восьмеричной и шестнадцатеричной системы по сравнению с двоичной
Восьмеричная и шестнадцатеричная системы счисления



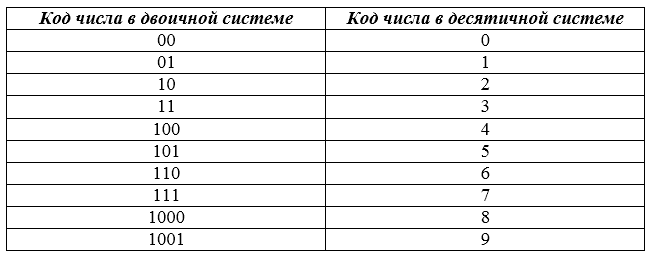
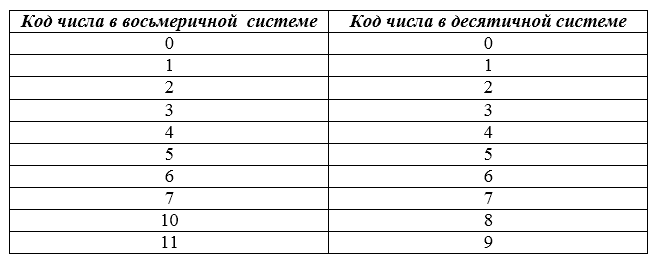
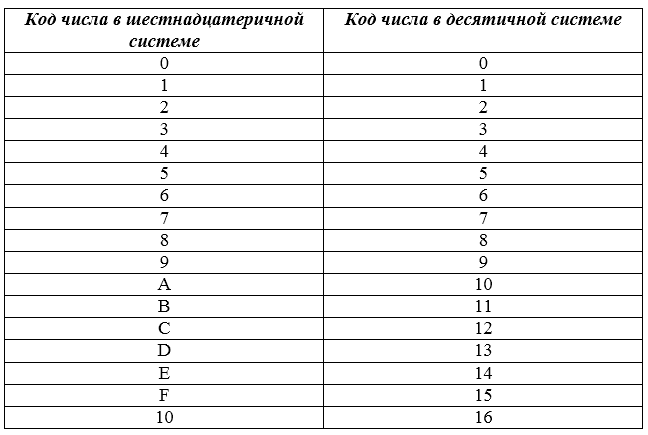
Такие системы счисления относятся к двоично-кодированным системам, когда основание системы счисления представляют целые степени двойки: 2 3 — для восьмеричной и 2 4 — для шестнадцатеричной систем счисления. Изображения целых чисел в восьмеричной и шестнадцатеричной системах счисления вместе с их двоичным и десятичными эквивалентами представлены в табл. 2.4 и 2.6
Большим достоинством восьмеричной и шестнадцатеричной систем счисления является:
-возможность более компактно представить запись двоичного числа. Запись одного и того же двоичного числа в восьмеричной в 3 раза, а в шестнадцатеричной системе в 4 раза короче двоичной;
-сравнительно просто осуществляется преобразование чисел из двоичной в восьмеричную и шестнадцатеричную системы и наоборот.
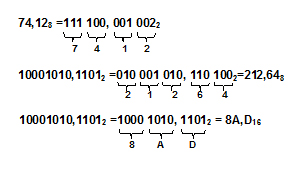
Действительно, так как для восьмеричного числа каждый разряд представляется группой из трех двоичных разрядов (триад), а для шестнадцатеричного — группой из четырех двоичных разрядов (тетрад), то для такого преобразования достаточно объединить двоичные цифры в группы по 3 и 4 бита соответственно, продвигаясь от разделительной запятой вправо и влево. При этом в случае необходимости добавляют нули в начале и в конце числа и каждую такую группу — триаду или тетраду — заменяют эквивалентной восьмеричной или шестнадцатеричной цифрой.
Указанные достоинства восьмеричных и шестнадцатеричных систем счисления определили использование их при составлении программ для более короткой и удобной записи двоичных чисел, команд и специальных двоичных слов, с которыми оперирует ЭВМ. Особенно оказалось удобным использование шестнадцатеричной системы, когда разрядность чисел и команд выбрана кратной байту, при этом каждый двоичный код байта запишется в виде 2-разрядного шестнадцатеричного числа.
Использование шестнадцатеричной системы счисления в ЭВМ общего назначения, как будет видно из дальнейшего изложения, позволяет расширить допустимый диапазон представления нормализованных чисел.
Шестнадцатеричная система счисления.
По формуле (2.2) шестнадцатеричное число можно представить так:
Двоичная, восьмеричная и шестнадцатеричная системы счисления
В настоящее время общепринятой стала арабская десятичная система счисления, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Так было не всегда, в Китае, например, долгое время пользовались пятеричной системой счисления.
Однако для использования в ЭВМ десятичная система слишком сложна, так как для ее применения необходимо подобрать технические способы изображения десяти различных цифр. С точки зрения технической реализации компьютера, гораздо проще работать всего с двумя цифрами двоичной системы: 0 и1.
Преимущества двоичной системы:
· для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.);
· представление информации посредством только двух состояний надежно и помехоустойчиво;
· возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
· двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел. Кроме двоичной широко используются системы с основанием, являющимся целой степенью числа 2 (табл.3.1), а именно:
Таблица 3.1. Соответствие первых 16 чисел в различных системах счисления
| Система счисления | |||
| 10-я | 2-я | 8-я | 16-я |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).
Чтобы перевести восьмеричное или шестнадцатеричное число в двоичную систему достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр) из табл.3.1:
Пример 3.1.
Для перевода числа из двоичной системы в восьмеричную или шестнадцатеричную необходимо выполнить предыдущую операцию в обратном порядке: разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
Дата добавления: 2019-10-16 ; просмотров: 340 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Двоичная, восьмеричная и шестнадцатеричная системы счисления
Вы будете перенаправлены на Автор24
Данные системы счисления относятся к позиционным.
Двоичная система счисления
Используя двоичную систему счисления, можно закодировать любое натуральное число, представляя его как последовательность нулей и единиц. В двоичном виде можно представить не только числа, но и любую другую информацию: тексты, изображения, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что оно легко реализуется технически.
Готовые работы на аналогичную тему
Другой единицей измерения информации является байт.
Достоинства двоичной системы счисления заключаются в ее простоте, благодаря которой она широко используется в технике. Устройства, работающие в двух состояниях (включено, выключено), наиболее помехоустойчивы, и, как следствие, более надежны.
Восьмеричная система счисления
В таблице приведены соответствия чисел в восьмеричной и десятичной системах.
В технике данная система находит широкое применение, так с помощью нее можно компактно записывать двоичные числа.
Шестнадцатеричная система счисления
В таблице приведены соответствия чисел в шестнадцатеричной и десятичной системах.
Почему восьмеричное и шестнадцатеричное? Компьютеры используют двоичные числа и десятичные дроби человека
Почему мы используем другие базы, которые не являются ни двоичными (для компьютеров), ни десятичными (для людей)?
Компьютеры в конечном итоге представляют их в двоичном формате, и люди настоятельно предпочитают получать их десятичное представление. Почему бы не придерживаться этих двух баз?
Восьмеричное (основание-8) и шестнадцатеричное (основание-16) числа являются разумным компромиссом между компьютерами, использующими двоичную (основание-2) систему, и десятичной (основание-10) системой, которую использует большинство людей.
Компьютеры плохо разбираются в нескольких символах, поэтому для них подходит база 2 (где у вас всего 2 символа), в то время как более длинные строки, числа с большим количеством цифр, представляют меньшую проблему. Люди очень хороши с несколькими символами, но не так хороши в запоминании длинных строк.
Восьмеричное и шестнадцатеричное используют преимущество человека, заключающееся в том, что они могут работать с большим количеством символов, в то время как он все еще легко конвертируется назад и вперед между двоичными числами, потому что каждая шестнадцатеричная цифра представляет 4 двоичные цифры ( ), а каждая восьмеричная цифра представляет 3 ( 8 = 2 3 ). Я думаю, что hex побеждает восьмеричное, потому что его легко использовать для представления байтов и 16/32/64-битных чисел. 16 = 2 4 ‘ role=»presentation»> 16 = 2 4 8 = 2 3 ‘ role=»presentation»> 8 = 2 3
Мы используем их для удобства и краткости.
Итак, скажем, вам нужны 64-битные адреса памяти. Вы можете просмотреть все 64 двоичных разряда или сжать их до 16 шестнадцатеричных цифр. Часто вам не нужно сравнивать несколько адресов, чтобы увидеть, совпадают ли они или смежные. Вы бы предпочли посмотреть на 64 бит или 16 цифр?
Вступление
При рассмотрении представления чисел применяется то же самое. Внутри компьютера все является двоичным на самом низком уровне, хотя для некоторых приложений могут использоваться странные представления.
За пределами компьютера мы используем любое понятное человеку представление, в зависимости от удобства человека относительно вида представленной ценности. Двоичное представление часто слишком длинное и неструктурированное, чтобы его можно было легко прочитать и записать, что позволяет заменить его на шестнадцатеричное или восьмеричное. Выбор часто может быть связан с тем, как информация структурирована в двоичном слове, которое не обязательно должно представлять число.
Более широкий взгляд
2 n ‘ role=»presentation»> 2 N системы, в основном двоичные, восьмеричные и шестнадцатеричные.
Суть вопроса, похоже, никоим образом не ограничена компьютерами, а люди использовали и продолжают использовать несколько других систем нумерации. Некоторые из них даже используются в компьютерах, например, при работе с длинными целыми числами (не говоря уже о нецелых числах ).
Первое замечание состоит в том, что когда люди считают тысячи или миллионы как единое целое, это все еще считается десятичным числом, потому что это степени 10. Поэтому можно задаться вопросом, почему восьмеричное или шестнадцатеричное не следует считать просто вариацией двоичного числа. Одной из возможных причин может быть количество символов, используемых для представления чисел (хотя это спорный вопрос, как мы увидим в других системах).
Эти двухосновные системы называются биквинарными или квадрикунарными системами. Чистая квина редко используется.
Римская цифра может рассматриваться как бинарная система (которая показывает, как с ними делать арифметику). Китайские и японские счеты используют би-квинари. Quadri-Quinary был использован майя.
Причин для использования системы, вероятно, много. Одна веская причина в том, что это был первый местный проект, и теперь люди привыкли к нему. Например, можно также задаться вопросом, почему англоговорящие люди все еще используют чрезвычайно странную систему нумерации при попытке измерить расстояния. Можно утверждать, что это вопрос нескольких единиц, а не нумерации, но это очень слабое замечание. Числа используются в основном для измерения вещей.
Другими причинами сохранения системы является удобство в данном контексте. Может быть компромисс между количеством различных символов или позиций на счетах и количеством символов, необходимых для формирования достаточно больших чисел. База 2 работает с 2 различными символами, но имеет много случаев, что может быть неудобно для представления материала. Vigesimal base 20 потребует двадцать символов и очень большие таблицы умножения, которые люди не помнят. Но би-квинарная или квадри-кинарная система намного более управляема, особенно для построения счётов. Чистая система семейств, вероятно, была бы еще лучше, но она идет вразрез с привычками и интуицией, основанными на физиологии. И всегда приятно иметь возможность считать пальцами, когда мы не знаем ничего лучше.
Одной из очень старых и очень распространенных систем является система шестидесятых, используемая для измерения времени и углов (но мы знаем, что они связаны через вращение Земли). Он использует основание 60, но не использует 60 символов, поскольку это слишком много. Поэтому он использует другую систему для представления своих синболов (например, десятичную систему).
Круг можно разделить на 6 частей, соответствующих углам 60 градусов, которые проще всего построить с равносторонними треугольниками. Тогда каждый градус составляет 60 минут дуги, каждый делится на 60 секунд.
Учитывая происхождение, это была довольно удобная система, в то время как математика едва вступала в детство. Не только угол 60⁰ легко рисовать, но и угол 60 имеет много факторов, так что он позволяет делить на целые числа без остатка.
12 × 5 = 60 ‘ role=»presentation»> 12 × 5 знак равно 60
Почему мы до сих пор используем половозрелую систему. Я думаю, что мы просто привыкли к этому, и у нас может быть слишком много конфликтующих вопросов, чтобы изменение было полностью оправданным.
Двоичная, восьмеричная и шестнадцатеричная системы счисления
Показал полезность применения двоичной системы немецкий математик Г. Лейбниц в 1703 г. Однако лишь благодаря работам Дж. Фон Неймана, опубликованным в 1940-х гг., двоичная система получила практическое использование при создании компьютерных средств.
В современной вычислительной технике, в устройствах автоматики и связи используется в основном двоичная система счисления, что обусловлено рядом преимуществ перед другими системами. Так, для ее реализации нужны технические устройства лишь с двумя устойчивыми состояниями, например материал намагничен или размагничен. Это обеспечивает более надежное и помехоустойчивое представление информации, дает возможность применения аппарата булевой алгебры для выполнения логических преобразований информации. Кроме того, арифметические операции в двоичной системе счисления выполняются наиболее просто.
Недостаток двоичной системы – быстрый рост числа разрядов, необходимых для записи больших чисел. Этот недостаток имеет существенное значение. Если возникает необходимость кодировать информацию “вручную”, например при составлении программы на машинном языке, используют восьмеричную или шестнадцатеричную системы счисления.
Примеры изображения чисел в данных системах счисления представлены в таблице 4.2.
Представление чисел в двоичной, восьмеричной и
Шестнадцатеричной системах счисления
| 10-ичная | 2-ичная | 8-ичная | 16-ичная |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления осуществляется путем замены каждой цифры эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).







Чтобы перевести число из двоичной системы счисления в восьмеричную или шестнадцатеричную, его нужно разбить влево или вправо от запятой на триады ( для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной или шестнадцатеричной цифрой.





Пример 7. Переведем число 10101001,101112 в шестнадцатеричную систему счисления.




Выполнение арифметических операций в двоичной, восьмеричной и шестнадцатеричной системах счисления
Правила выполнения арифметических операций сложения, вычитания, умножения и деления в 2-, 8- и 16-ичной системах счисления будут такими же, как и в десятичной системе, только надо пользоваться особыми для каждой системы таблицами сложения и умножения.
Таблицы сложения для 2-ичной, 8-ичной и 16-ичной систем счисления представлены в таблицах 4.3-4.5.
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Сложение в двоичной системе
Сложение в восьмеричной системе