В чем заключается принцип гюйгенса френеля
В чем заключается принцип теории Гюйгенса Френеля
Как известно, свет проявляет свойства, волны и частицы. Одна из теорий, описывающих его поведение — это волновая теория света. Важнейший постулат этой теории — принцип Гюйгенса-Френеля. Он описывает и объясняет распространение волн, частным случаем которых и является свет — электромагнитное излучение в оптическом диапазоне.
Суть принципа Гюйгенса-Френеля
Это утверждение объясняет и описывает то, как распространяются колебания, например, свет. Оно состоит из двух частей. Первую часть (принцип Гюйгенса) предложил Христиан Гюйгенс в 1678 году. Он предположил, что при распространении излучения из каждой точки волнового фронта начинают исходить новые сферические волны.
Волновой фронт — это поверхность, на которой возмущение находится в одинаковой фазе. Проще говоря, это граница пространства, в котором уже распространилось возмущение. Например, если бросить камень в воду, пойдут круги — волны. Их фронт в этом случае — это самый внешний круг.
Огюстен Жан Френель в 1815 году развил предположение Гюйгенса.
Важно! Его дополнение заключается в том, что поле, получившееся при распространении возмущения, создается интерференцией вторичных колебаний, которые имеют одинаковую амплитуду. Огибающая вторичных волн дает положение волнового фронта через небольшой промежуток времени.
Интерференция — это наложение волн друг на друга. При этом в одних участках колебания они взаимно усиливают друг друга, в других ослабляют. Поэтому для света получается картина из светлых и темных полосок. Пример этого кольца Ньютона, картина из концентрических кругов, получающаяся, если плоско-выпуклую линзу положить на стеклянную пластинку.
Чтобы можно было наблюдать картину интерференции, излучение должно быть когерентным. Это значит, что оно должно иметь постоянную разность фаз и давать колебания такой же частоты, если их сложить.
Утверждение, сделанное Гюйгенсом, помогало определить только направление распространения возмущения и объясняло распространение света, как его описывает геометрическая оптика. Дополнение принципа Гюйгенса позволяет рассчитывать амплитуду и интенсивность.
Это интересно! Какие бывают системы отсчета в физике и что это такое
Краткая формулировка
Если говорить кратко, этот постулат заключается в следующем. Колебания в любой точке пространства — это результат интерференции возмущений, излученных точками на волновой поверхности.
Для любой точки пространства колебания — это наложение вторичных когерентных колебаний, излучаемых точками волнового фронта. Таким образом, в некоторых задачах можно один источник заменить на несколько одинаковых вторичных источников.
Применение
Рассматриваемое утверждение дает возможность объяснить различные оптические явления:
С помощью принципа Гюйгенса-Френеля можно рассчитать амплитуду и интенсивность светового излучения. Для этого используются методы зон Френеля.
Зоны Френеля
Это утверждение важно для решения задач по дифракция света по принципу Гюйгенса-Френеля. Строгое решение таких задач математически очень сложно, поэтому пользуются приближенными методами.
Благодаря открытиям Гюйгенса и Френеля в таких задачах можно заменить один первичный источник совокупностью вторичных источников.
Это существенно облегчает задачу, например, для сферического случая. Такой метод расчета называется методом зон Френеля.
Важно! Зоны Френеля — это участки, на которые делят поверхность, чтобы упростить расчет, например, амплитуды колебаний. На зоны можно разбить любую поверхность, через которую проходит свет.
Сферический случай
В случае сферической волны зоны Френеля выглядят как кольца. Для произвольной точки М их можно построить, проведя из этой точки сферы радиусы, различающиеся на 1/2 длины волны.
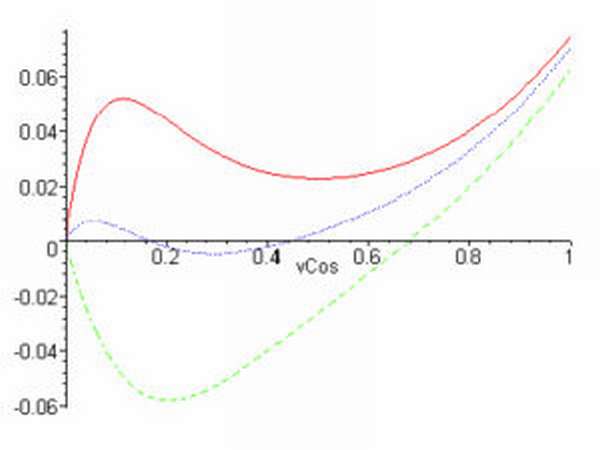
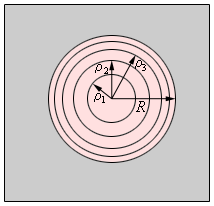
Для сферического случая можно посчитать радиус зоны. Это внешний радиус кольца.
Площади зон Френеля с небольшими номерами примерно одинаковы. Они не зависят от номера зоны m. Они считаются как разница площадей сегментов сферы. Если не углубляться в детали, площади зон Френеля в этом случае находят так. Нужно умножить длину волны на радиус сферического волнового фронта R, на расстояние до точки наблюдения a и на число пи, а затем поделить на сумму R и a.
Зоны Френеля находят применение в зонных пластинках со светлыми и темными кольцами-радиусами, соответствующими размерам зон. Они работают аналогично собирающей линзе.
Это интересно! Квантовые постулаты Нильса Бора: кратко об основных положениях
Дифракция
С помощью этого постулата объясняется дифракция света по принципу Гюйгенса-Френеля — огибание ими небольших предметов. Для света он дает обоснование того, почему возмущения распространяются и в область геометрической тени. Если бы они не огибали предметы, мы бы никогда не увидели полутени, все тени были бы резкими, как предполагает геометрическая оптика. Но реальная картина отличается от предположений геометрической оптики.
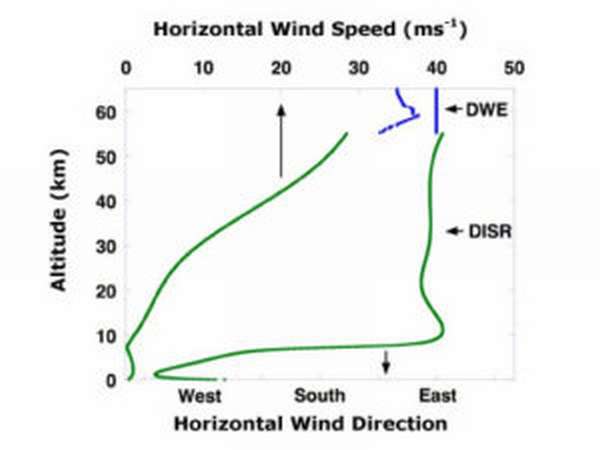
Пример — плоская волна, падающая на плоскость с отверстием. Когда она проходит через отверстие, все точки фронта излучают вторичные сферические колебания. С помощью построения огибающей увидим, что фронт волны оказывается там, куда согласно геометрической оптике свет попадать не должен.
Френель обосновал явление дифракции света по принципу Гюйгенса-Френеля и создал метод ее расчета. Развив принцип Гюйгенса, он установил, что:
Дифракция на прямоугольной щели
Прямоугольную щель можно поделить на N зон в виде узких полосок, параллельных ее длинной стороне. Если наблюдатель находится далеко от источника, то задача сводится к расчету интерференции от N одинаковых источников.
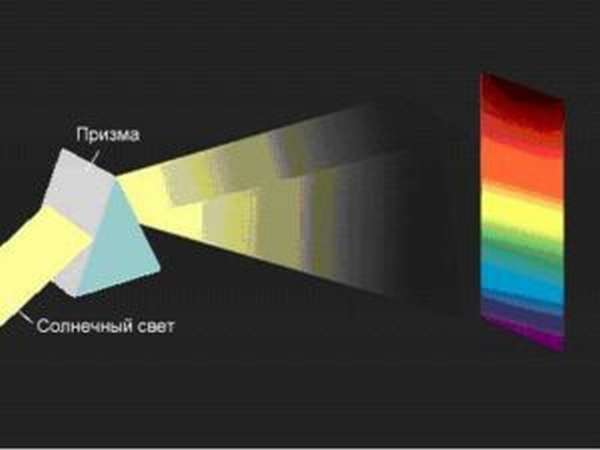
В таком случае интерференционная картина выглядит как светлые и темные полосы. Наиболее яркая светлая полоса — главный максимум — находится в центре.
Преломление
Когда свет попадает из одной среды в другую, например, из воздуха в воду, он меняет направление, т.е. преломляется. Согласно принципу Гюйгенса-Френеля на границе сред из каждой точки исходит вторичное излучение.
Из принципа Гюйгенса можно получить, что показатель преломления равен отношению скоростей светового колебания в одной и другой среде. Также можно найти и угол, на который отклоняется свет.
Это интересно! Изучаем термины: энтропия – что же это такое простыми словами
Видео
В интернете можно найти видео, демонстрирующие, как работает принцип Гюйгенса-Френеля. Например, наглядная демонстрация для отражения плоской волны от поверхности доказывает, что угол падения и угол отражения равны.
Если волна падает на плоскость, отражаясь от нее, различные точки волновой поверхности доходят до плоскости неодновременно. Начинают распространяться вторичные колебания.
Касательная к ним — это и есть волновой фронт отраженного колебания. Решив простую геометрическую задачу о равенстве треугольников, можно установить, что углы, под которыми излучение падает и отражается, равны.
Можно построить изображение источника в плоском зеркале. Фронт отраженного возмущения будет сферой с центром в некоторой точке. Эта точка и будет мнимым изображением плоского источника в зеркале.
Можно найти видео, иллюстрирующие и другие физические явления. Например, можно пронаблюдать зоны Френеля для электромагнитного колебания. Также можно найти лекции, посвященные принципу Гюйгенса-Френеля и другим вопросам оптики.
Это интересно! Формулировки законов Исаака Ньютона: кратко и понятно
Полезное видео
Заключение
Принцип Гюйгенса-Френеля дает возможность объяснить такие оптические явления, как рефракцию, дифракцию, распространение света по прямой, интерференцию. С его помощью можно приближенно решать задачи оптики, которые очень трудно решить точными методами. Это утверждение — основной постулат волновой теории и применимо не только к распространению светового излучения, но и к другим волновым процессам.
Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля
Дифракция света – это явление отклонения света от прямолинейного направления его распространения во время прохождения рядом с препятствиями.
Из опыта видно, что определенные условия влияют на захождение геометрической тени на область.
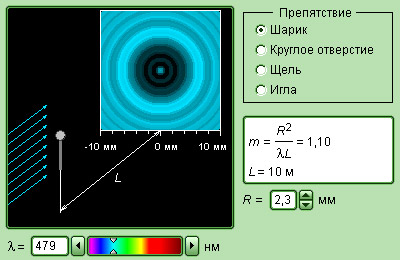
Когда на пути встречается препятствие в виде диска, шарика или круглого отверстия, тогда экран, расположенный на большом расстоянии, покажет дифракционную картину, то есть систему чередующихся светлых и темных колец. При отверстии линейного характера (щели или нити) экран показывает параллельные дифракционные полосы.
Принцип Гюйгенса-Френеля
Существование дифракционных явлений было задолго до времен Ньютона. Объяснение, основанное на корпускулярной теории, не давало должных результатов. Одним из первых объяснений явления дифракции, основанное на волновых представлениях, было дано Т. Юнгом. Еще в 1818 году была известна и развита количественная теория дифракционных явлений О. Френеля. Принцип Гюйгенса был заложен в основу. Он только дополнил при помощи идеи об интерференции вторичных волн.
Первоначальный вид данного принципа давал возможность нахождения положения фронтов в последующие моменты времени, иначе говоря, определял направление распространения волны. Это и есть принцип геометрической оптики. Впоследствии гипотеза Гюйгенса об огибающих вторичных волнах были заменены Френелем с помощью физически ясного положения, тогда вторичные волны в точке наблюдения интерферировали друг с другом.
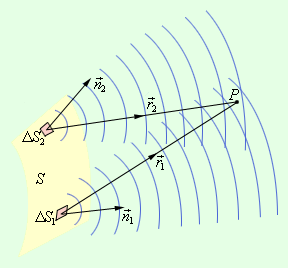
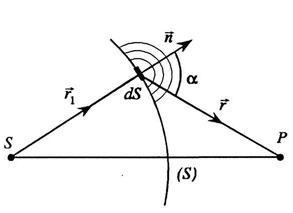
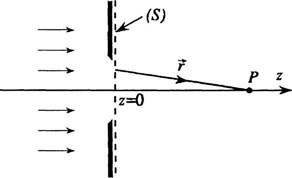
Принципом Гюйгенса-Френеля считалась гипотеза, которая была со временем подтверждена. При решении задач, где необходимо использовать данный принцип, получение результата достаточно точное. На иллюстрации изображен принцип Гюйгенса-Френеля.
Предположим, что поверхность S – положение волнового фронта в некоторый момент. Из теории волн известно, что он является поверхностью, где в заданных точках происходит колебание с одинаковым значением фазы. Волновыми фронтами плоской волны считают семейством параллельных плоскостей, которые перпендикулярно направлены относительно распространения волны. Волновые фронты сферической волны, которые испускаются при помощи точечного источника, относят к концентрическим сферам.
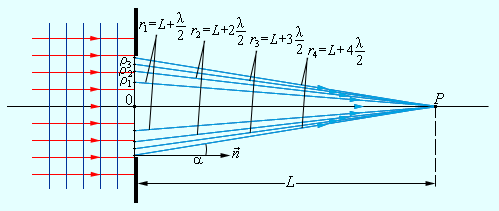
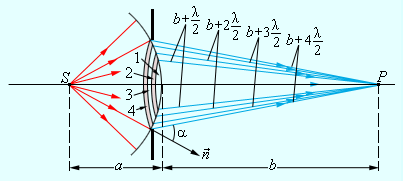
Для примера ниже приведена дифракционная задача прохождения плоской монохроматической волны, которая исходит от удаленного источника через отверстие с радиусом R непрозрачного экрана.
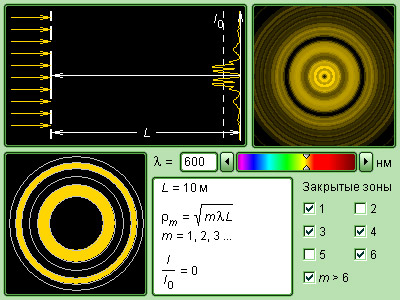
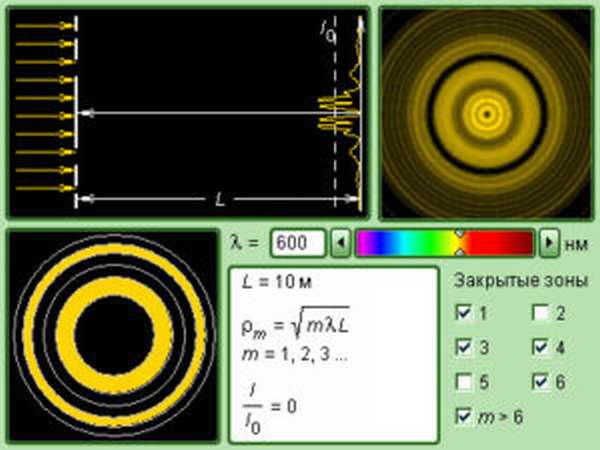
Чтобы расчеты были облегченными, волновая поверхность падающей волны разбивается на кольцевые зоны, называемыми зонами Френеля, исходя из правила: расстояния от границ соседних зон к точке Р имеют отличие на половину волны.
Зоны Френеля. Интерференционный максимум
Отличие от двух соседних точек расстоянием λ 2 говорит о том, что колебания, возбуждаемые этими зонами в состоянии противофазы. Соседние волны начинают гасить друг друга, а это приводит к тому, что суммарная амплитуда в точке запишется как:
Выражения в скобках равняются нулю, значит, амплитуда, вызванная волновым фронтом, равняется половине действий первой зоны.
Полученные пластинки обладают свойством фокусировки света, поэтому их называют зонными пластинками.
Круглый диск дает понять, что при дифракции зоны Френеля от 1 до m будут в закрытом состоянии. Отсюда получаем, что формула амплитуды колебаний примет вид:
Так как оптический диапазон имеет короткую волну, тогда соответственно зона Френеля также мала. Отчетливее проявление дифракционных явлений заметно при небольшом количестве зон на препятствии.
Получим формулы вида:
Когда количество зон Френеля из препятствия увеличивается, тогда дифракционные явления становятся незаметными:
Определение границы применимости геометрической оптики возможно при помощи заданного неравенства. При выполнении данного условия узкий пучок света может быть сформирован.
Отсюда следует вывод, что волновая оптика – это предельный случай геометрической.
При расчете видно, что радиусы ρ m зон Френеля на волне сферического фронта запишется, как
Выводы по теории Френеля справедливы.
Дифракция и интерференция света применима к любым волнам, так как имеется общность закономерностей. Начало XIX века – это было время, когда ученые только начинали изучать волны, а физическая природа света еще не была раскрыта.
В чем заключается принцип гюйгенса френеля
Дифракция света – в узком, но наиболее употребительном смысле – огибание лучами света границы непрозрачных тел (экранов); проникновение света в область геометрической тени. Наиболее рельефно дифракция света проявляется в областях резкого изменения плотности потока лучей: вблизи каустик, фокуса линзы, границ геометрической тени и др. дифракция волн тесно переплетается с явлениями распространения и рассеяния волн в неоднородных средах.
Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями, размеры которых сравнимы с длиной волны, и связанных с отклонениями от законов геометрической оптики.
Огибание препятствий звуковыми волнами (дифракция звуковых волн) наблюдается нами постоянно (мы слышим звук за углом дома). Для наблюдения дифракции световых лучей нужны особые условия, это связано с малой длиной световых волн.
Между интерференцией и дифракцией нет существенных физических различий. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн.
Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени.
Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис. 9.1). Каждая точка участка волнового фронта, выделенного отверстием, служит источником вторичных волн (в однородной изотопной среде они сферические).
Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т.е. волна огибает края отверстия.
Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде и интенсивности волн, распространяющихся по разным направлениям.
Решающую роль в утверждении волновой природы света сыграл О. Френель в начале XIX века. Он объяснил явление дифракции и дал метод ее количественного расчета. В 1818 году он получил премию Парижской академии за объяснение явления дифракции и метод его количественного расчета.
Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.
При рассмотрении дифракции Френель исходил из нескольких основных положений, принимаемых без доказательства. Совокупность этих утверждений и называется принципом Гюйгенса–Френеля.
Согласно принципу Гюйгенса, каждую точку фронта волны можно рассматривать как источник вторичных волн.
Френель существенно развил этот принцип.
· Все вторичные источники фронта волны, исходящей из одного источника, когерентны между собой.
· Равные по площади участки волновой поверхности излучают равные интенсивности (мощности).
· Каждый вторичный источник излучает свет преимущественно в направлении внешней нормали к волновой поверхности в этой точке. Амплитуда вторичных волн в направлении, составляющем угол α с нормалью, тем меньше, чем больше угол α, и равна нулю при 
.
· Для вторичных источников справедлив принцип суперпозиции: излучение одних участков волновой поверхности не влияет на излучение других (если часть волновой поверхности прикрыть непрозрачным экраном, вторичные волны будут излучаться открытыми участками так, как если бы экрана не было).
Используя эти положения, Френель уже мог сделать количественные расчеты дифракционной картины.
Формулировка принципа Гюйгенса-Френеля
Принцип Гюйгенса-Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых.
Описание принципа Гюйгенса
Что объясняет
В 1678 году Христиан Гюйгенс предположил, что каждая точка поверхности, куда добирается волна света, становится вторичным источником, отражающим волну. Это объясняло поведение световых волн в прозрачных средах и при контакте с зеркальными поверхностями, но не соответствовало принятой научным сообществом на тот момент корпускулярной теории света.
Основная проблема принципа
Принципа Гюйгенса недостаточно для полного объяснения такого явления, как дифракция. Интерференция в принципе Гюйгенса не учитывалась вовсе.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Работа Френеля над принципом Гюйгенса
Что он изменил и добавил
Большинство маститых учёных — и среди них Жан Био, Пьер Лаплас, Симеон Пуассон — вслед за Исааком Ньютоном считали свет потоком частиц, или корпускул. В рамках корпускулярной теории были сделаны самые значительные открытия в оптике, например, обнаруженная в 1808 году Этьеном Малюсом поляризация света при отражении.
Волновая теория света не могла объяснить поляризацию и двойное лучепреломление, в то время как у её противников имелись на этот счет хоть и громоздкие, но все же вполне приемлемые гипотезы. В 1815 году Огюстен Френель сопоставил волновую и корпускулярную теории света и, признав преимущества корпускулярной в объяснении прямолинейного распространения света, доказал, что те же явления можно объяснить и в рамках гипотезы колебаний. Через некоторое время, исследуя явления поляризации, Френель понял, что их можно объяснить, только приняв предположение о поперечном характере световых волн. Теоретические рассуждения Гюйгенса о том, как волны огибают препятствия, Френель заменил доказательством интерференции вторичных волн.
Формулировка
Дополнение Френеля к принципу Гюйгенса доказывает, что каждый элемент волнового фронта можно считать центром возбуждения вторичных сферических волн. Световое поле в каждой точке пространства будет определяться их интерференцией.
Что объясняет принцип Гюйгенса-Френеля
Независимость волны от источника
Каждая точка поверхности, куда попадает волна, становится вторичным источником волн. Эти волны, попадая в свободное пространство, при движении вперед интерферируют только друг с другом и усиливают друг друга в одинаковых фазах. При движении назад они гасятся при интерференции с первичной, прямой волной. Фазы вторичных волн отличаются от фаз первичных.
Явление дифракции
Если внимательно взглянуть на пятно света, прошедшего через узкое отверстие, можно заметить, что его граница окружена чередующимися тёмными и светлыми полосками. Возникают они за счёт дифракции на краях отверстия.
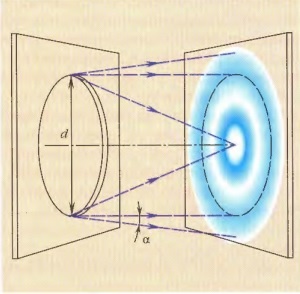
Рассмотрим сечение круглого волнового пучка, выходящего из отверстия диаметром d. Разбив пучок на множество маленьких вторичных источников, проследим, как ведут себя волны, приходящие от любого из них в разные точки пространства. Если выбрать точку наблюдения близко к оси пучка, то вторичные волны в этой точке окажутся в фазе и при сложении будут усиливать друг друга. По мере увеличения расстояния от оси разность фаз между самым близким и самым дальним источниками начнет увеличиваться, и можно обнаружить точку, где волны находятся в противофазе, гасят друг друга.
Чем дальше точка наблюдения от оси пучка, тем больше в нее приходит таких рассогласованных вторичных волн, тем слабее суммарная волна. Точный расчет показывает, что вторичные волны полностью гасят друг друга при распространении под углом к оси пучка. Следовательно, пучок из цилиндрического превращается в конический. Этот угол называют углом дифракции.
Несмотря на то, что абсолютно точно описать взаимодействие волн в процессе дифракции можно только в рамках векторной электромагнитной теории, скалярный принцип Гюйгенса-Френеля достаточно адекватно описывает формирование оптического изображения и применяется для решения большинства практических задач. Большая точность необходима лишь для описания работы субдлинноволновых оптических инструментов, а также оптических систем с большой числовой апертурой.
Решение уравнения по принципу
Интегральная формулировка принципа
Формулировка через интеграл по траекториям — это способ найти множество траекторий вторичных волн. Этот способ на основе принципа Гюйгенса-Френеля был адаптирован для расчета бесконечного множества траекторий квантовой амплитуды.
Сущность метода заключается в делении поверхности на столь малые части, чтобы их можно было принять за материальные точки, и последующем суммировании величин по всем участкам изменения конкретной величины. Волновой фронт, расходящийся от точечного источника, имеет вид сферы.
где \(f_0\left(\overrightarrow
\(K(\alpha)\) — коэффициент наклона;
\(\lambda\) — длина волны.
Когда в задаче идет речь о дифракции, нужно применить постулат о граничных условиях и проинтегрировать вышеприведенное выражение по поверхности S, разделяя затененные и не прикрытые экраном участки.
Определение комплексной амплитуды первичной волны в данном случае выглядит следующим образом:
Тогда комплексную амплитуду в точке наблюдения можно найти по формуле:
В оптических задачах часто используется метод зон Френеля. Он позволяет с помощью геометрических построений определить закономерности распределения интенсивности волн. С целью упрощения расчетов волновую поверхность делят на кольцевые зоны.
Примеры решения задач
Задача 1
Вычислить суммарную амплитуду плоской монохроматической дифрагированной волны на щели, плоскость которой перпендикулярна распространению волны, при условии, что экран расположен далеко от щели.
Решение
Так как экран далеко, можно считать, что для участка щели с координатой у расстояние до точки наблюдения равно \(у\;\times\;\sin\left(\psi\right).\)
Изменение угла psi между нормалью к плоскости щели и направлением наблюдения приведет к изменению угла d\varphi между векторами комплексных амплитуд волн, пришедших от соседних участков щели.
Чтобы найти суммарную амплитуду, нужно сложить комплексные числа с одинаковыми амплитудами и разными фазами \(\frac<2\mathrm\pi>\lambda\;\times\;у\;\times\;\sin\left(\psi\right).\)
Ответ: суммарную амплитуду можно вычислить по формуле:
\(E’ = \int_<0>^
Задача 2
Квадратное отверстие со стороной 0,2 см освещено параллельным пучком нормально падающих лучей света.
Найти размер изображения отверстия на экране, параллельном отверстию и удаленном от него на 50 метров. За границу изображения на экране принять положение дифракционного максимума первого порядка для наиболее отклоняемых лучей (видимый спектр от 400 до 700 нм).
Решение
Напряженность электрического поля волны в данных условиях можно вычислить с помощью формулы:
Введем углы дифракции \(\vartheta_1\) и \(\vartheta_2\) :
Так как расстояние l достаточно велико, углы дифракции малы, соответственно, есть основания предполагать, что их тангенс примерно равен синусу. Тогда формула напряженности поля с подставленными значениями будет выглядеть так:
Интегрировав выражение, получим:
Угловое выражение дифракционных максимумов первого порядка:
Вычислим линейное расстояние D между оптической осью системы и дифракционным максимумом:
Подставим в выражение максимальную длину волны видимого света, 700 нм.
Ответ: длина стороны квадрата на экране \(2D\;\approx\;5\;см.\)