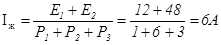В чем заключается расчет построение потенциальной диаграммы
Потенциальная диаграмма электрической цепи
Для построения потенциальной диаграммы выбирают замкнутый контур. Этот контур разбивают на участки таким образом, чтобы на участке находился один потребитель или источник энергии. Пограничные точки между участками необходимо обозначить буквами или цифрами.
Произвольно заземляют одну точку контура, её потенциал условно считается нулевым. Обходя контур по часовой стрелке от точки с нулевым потенциалом, определяют потенциал каждой последующей пограничной точки как алгебраической суммы потенциала предыдущей точки и изменения потенциала между этими соседними точками.
Изменение потенциала на участке зависит от состава цепи между точками. Если на участке включен потребитель энергии (резистор), то изменение потенциала численно равно падению напряжения на этом резисторе. Знак этого изменения определяют направлением тока. При совпадении направлений тока и обхода контура знак отрицательный, в противном случае он положительный.
Если на участке находится источник ЭДС, то изменение потенциала здесь численно равно величине ЭДС данного источника. При совпадении направления обхода контура и направления ЭДС изменение потенциала положительно, в противном случае оно отрицательно.
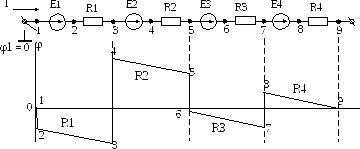
После расчета потенциалов всех точек строят в прямоугольной системе координат потенциальную диаграмму. На оси абсцисс откладывают в масштабе сопротивление участков в той последовательности, в которой они встречались при обходе контура, а по оси ординат – потенциалы соответствующих точек. Потенциальная диаграмма начинается с нулевого потенциала и заканчивается после обхода контура таковым.
Построение потенциальной диаграммы электрической цепи
В данном примере потенциальную диаграмму строим для первого контура цепи, схема которой изображена на рисунке 1.
Рис. 1. Схема сложной электрической цепи
В рассматриваемый контур входят два источника питания E1 и E2, а также два потребителя энергии r1, r2.
Следующей точкой на пути обхода контура будет точка b. На участке ab находится источник ЭДС Е1. Так как на данном участке мы идем от отрицательного полюса источника к положительному, то потенциал повышается на величину Е1 :
При переходе от точки b к точке c происходит уменьшение потенциала на величину падения напряжения на резисторе r1 (направление обхода контура совпадает с направлением тока в резисторе r1) :
При переходе к точке d потенциал возрастает на величину падения напряжения на резисторе r2 (на этом участке направление тока встречно направлению обхода контура) :
φ d = φ c + I2r2 = 12 + 0 х 4 = 12 В
Потенциал точки а меньше потенциала точки d на величину ЭДС источника E2 (направление ЭДС встречно направлению обхода контура) :
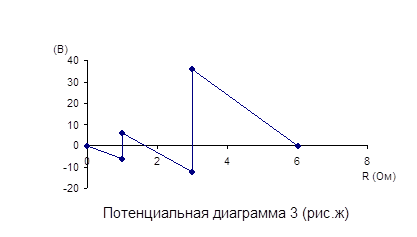
Результаты расчета используют для построения потенциальной диаграммы. На оси абсцисс откладывают сопротивление участков в той последовательности, как они встречаются при обходе контура от точки с нулевым потенциалом. Вдоль оси ординат откладывают рассчитанные ранее потенциалы соответствующих точек (рисунок 2 ).
Потенциальная диаграмма онлайн. Help.
Бесплатная онлайн программа для построения потенциальной диаграммы, цепей постоянного тока.
Программа позволяет произвести расчет и построение потенциальной диаграммы для выбранного контура цепи.
Рис. 1. Схема фрагмента электрической цепи — замкнутого контура
Перетаскиваем необходимые элементы на рабочее поле программы:
Вводим параметры элементов:
Параметры элемента R1
В поле «Номер тока на схеме» указываем номер тока проходящего через резистор, в поле «Ток» — величину тока.
«Номер тока на схеме» = 1;
Если через элементы проходит одинаковый ток — то указываем одинаковые значения в этих элементах.
Нажимаем кнопку РАССЧИТАТЬ и получаем результат:
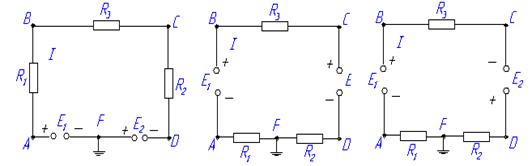
Примем положительное направление обхода схемы – по часовой стрелке.
Схема разбита на участки, каждый из которых содержит либо источник ЭДС, либо резистор.
Примем нулевым потенциал точки A
φA = 0 В
Следующая точка согласно выбранному направлению движения – B.
Следующая точка согласно выбранному направлению движения – C.
Следующая точка согласно выбранному направлению движения – D.
Следующая точка согласно выбранному направлению движения – E.
Следующая точка согласно выбранному направлению движения – A.
Построение потенциальной диаграммы
Потенциальная диаграмма – это графическое изображение изменения потенциала в электрической цепи в зависимости от сопротивлений участков при обходе замкнутого контура, то есть график зависимости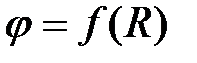 
.
По оси абсцисс в масштабе откладываются сопротивления между характерными точками, а по оси ординат – их потенциалы. Потенциальная диаграмма позволяет определить напряжения между любыми точками цепи, если на оси ординат отмечены потенциалы соответствующих точек.
Чтобы построить потенциальную диаграмму, необходимо выполнить следующее:
— рассчитать электрическую цепь;
— разбить цепь на характерные точки, между которыми содержится один элемент (сопротивление или ЭДС);
— заземлить любую точку, потенциал в которой будет равен нулю, а потенциалы других точек вычислить. Если Н.О. совпадает с направлением тока, то потенциал уменьшается, при совпадении Н.О с направлением ЭДС потенциал увеличивается;
— на оси абсцисс в выбранном масштабе откладываются сопротивления между характерными точками, начало координат должно соответствовать нулевой точке;
— на оси ординат в масштабе откладываются потенциалы характерных точек;
— полученные точки соединяются прямыми линиями.
В данной задаче потенциальная диаграмма строится для внешнего контура исходной электрической цепи (рис.1.2).
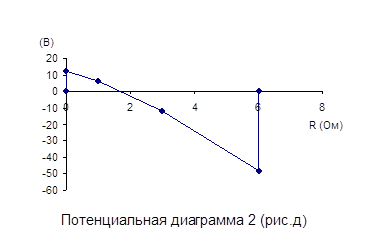
Заземляется точка а (потенциал в этой точке равный нулю), а далее рассчитываются потенциалы в каждой отдельной точке схемы и строиться потенциальная диаграмма (рис.1.3).
Рисунок 1.3 – Потенциальная диаграмма для внешнего контура схемы, изображенной на рисунке 1.2.
Варианты для задачи 1
Для схемы, соответствующей вашему варианту, изображенной на рисунке 1.1 – 1.30 необходимо выполнить следующее расчеты:
1. Составить систему уравнений для определения токов в схеме по первому и второму закону Кирхгофа.
2. Определить все токи методом узловых потенциалов.
3. Определить все токи методом контурных токов (МКТ).
4. Записать баланс мощностей для преобразованной схемы.
5. Построить потенциальную диаграмму в масштабе для внешнего контура схемы (исходной или преобразованной).
Потенциальная диаграмма.
Под потенциальной диаграммойпонимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат откладывают потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.
Потенциальная диаграмма строится, когда все токи и напряжения в цепи рассчитаны.
Отношение напряжения к сопротивлению рассматриваемого участка цепи будет соответствовать тангенсу угла наклона прямых, определяющих изменение потенциала, к оси абсцисс. Но поскольку ток в данной схеме остается неизменным, то и наклон прямых одинаков.
Баланс мощностей
Вытекает из закона сохранения энергии. Условие энергетического баланса для любой электрической цепи постоянного тока выражается в виде равенства нулю суммы мощностей по всем элементам:
Уравнение баланса мощностей можно записать в иной форме:
.
Суммарная мощность, развиваемая источниками электрической энергии, равна суммарной мощности, потребляемой приемниками.
Первая обычно называется генерируемой мощностью, а вторая – потребляемой.
Потребляемая энергия в цепях постоянного тока связана с выделением на сопротивлениях при протекании тока теплоты и определяется в соответствии с законом Джоуля – Ленца: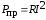 
.
Для идеального источника напряжения генерируемая мощность определяется как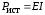 
, причем если направление тока совпадает с направлением ЭДС, то произведение берется со знаком «+». Это означает, что источник ЭДС доставляет в цепь энергию.
Если направление тока встречно направлению ЭДС, то источник не поставляет энергию, а потребляет ее (например, идет заряд аккумулятора). При этом произведение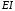 
в уравнение энергетического баланса входит со знаком «−».
 | Если источник неидеальный, то  |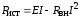
Для источника тока
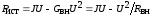 |  . Если направление тока источника совпадает с направлением напряжения, то 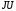 берется со знаком «+», в противном случае – со знаком «−». |
7 Определения в цепях переменного тока. Действующее значение тока, напряжения
Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.
В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение переменного тока.
Действующие значения тока и напряжения
Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?
При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.
Наиболее удобным оказалось введение понятий так называемыхдействующих значений тока и напряжения. В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.
Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.
Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р 2 r.
Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от (Im х sinωt) 2 х rза то же время.
Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √M,
Величина I называется действующим значением переменного тока.
Среднее значение i2 при переменном токе определим следующим образом.
Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.
Действующее значение переменного тока
Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины.
Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно1/2I 2 m. Следовательно, М = 1/2I 2 m
Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2
Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:
Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е).
На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.
Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.
При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √2 раз. От этого расположение векторов на диаграмме не изменяется.
; 
;
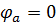
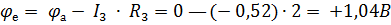
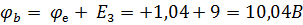
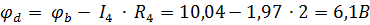
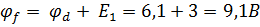
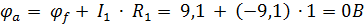
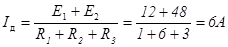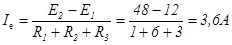