В чем заключается различие между точным и приближенным процентом
В чем заключается различие между точным и приближенным процентом
Начисление простых процентов
Начисление простых процентов обычно используется в двух случаях: при заключении краткосрочных контрактов (предоставлении краткосрочных кредитов и т.п.), срок которых не превышает одного года, и когда проценты не присоединяются к сумме долга, а выплачиваются периодически.
Ставка процентов обычно устанавливается в расчете за год, поэтому при продолжительности ссуды менее года необходимо выяснить какая часть процента уплачивается кредитору. Для этого величину п выражают в виде дроби
В этом случае наращенная сумма вычисляется по формуле:
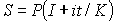
Возможно несколько вариантов расчета процентов, различающихся выбором временной базы К и способом измерения срока пользования ссудой.
Часто за базу измерения времени берут год, условно состоящий из 360 дней (12 месяцев по 30 дней в каждом). В этом случае говорят, что вычисляют обыкновенный или коммерческий процент. В отличие от него точный процент получают, когда за базу берут действительное число дней в году: 365 или 366 (год високосный).
Различные варианты временной базы и методов подсчета дней ссуды, приводят к следующим схемам расчета процентов, применяемых на практике:
— точные проценты с точным числом дней ссуды (британская схема 365/365, когда в году считается 365 дней, полугодие приравнивается к 182 дням и точная длительность месяцев). Используется в Великобритании, США, Португалии;
— обыкновенные проценты с точным числом дней ссуды (французская схема 365/360, в году принимается 360 дней и точная длительность месяцев). Используется во Франции, Бельгии, Испании;
— обыкновенные проценты с приближенным числом дней ссуды (германская схема 360/360, в году считается 360 дней и 30 дней в каждом месяце). Используется в Германии, России, США.
Поскольку точное число дней ссуды в большинстве случаев больше приближенного, то проценты с точным числом дней обычно больше, чем с приближенным.
Вариант расчета с точными процентами и приближенным измерением времени ссуды не применяется.
Точное и приближенное число дней для обыкновенных процентов связаны следующими зависимостями:
i 360 = 0,986301 × i365; i365 = 1,013889 × i360.
Пример 1.
Найти точное и приближенное число дней между 5 марта и 28 сентября.
По таблице (Приложение) 28 сентября является 271 днем, а 5 марта – 64 днем года. Поэтому точное число дней составляет
271 дн. – 64 дн. = 207 дн.
Найдем приближенное число дней между 5 марта и 28 сентября.
5 мес. × 30 дн. + (30 дн. – 5 дн.) + 28 дн. = 203 дн.
Между 5 марта и 28 сентября точное число дней составляет 207, приближенное – 203.
Ссуда в размере 3000 р. положена в банк под 10% годовых с 3 апреля по 29 ноября следующего года (год не високосный). Определить тремя способами наращенную сумму. Какой вариант наращения выгоден банку, а какой вкладчику.
Наращенную сумму найдем по формуле (1.5.).Рассмотрим различные варианты расчета:
1.Точные проценты с точным числом дней ссуды.
Точное количество дней – 604, временная база – 365 дней, тогда
S 1 = 3000 (1 + 0,1 × 604 / 365) = 3496,4 р.
2. Обыкновенные проценты с точным числом дней ссуды.
Точное количество дней – 604, временная база – 360 дней
S 2 = 3000 (1 + 0,1 × 604 / 360) = 3503,3 р.
3. Обыкновенные проценты с приближенным числом дней ссуды
Банку выгоден третий вариант расчета наращения. Заемщику – второй вариант расчета наращения.
Банковское дело
Сложные проценты
В банковской практике возможно использование сложного процента, как правило, при долгосрочном кредитовании, когда начисленные суммы не выплачиваются кредитору до окончания сделки, а увеличивают основную сумму долга. В отечественной практике метод начисления сложных процентов получил наибольшее распространение по депозитным счетам частных лиц.
При использовании этого метода размер начисленных средств включается в задолженность и на них продолжает начисляться процент. Формулу для начисления сложных процентов и определения обшей суммы задолженности можно представить в виде :
S = Р(1 + i) n — при постоянной ставке процентов;
S = Р(1 + i) n • (1 + i2) n 2 …(l + ik) n k — при переменной ставке процентов;
иде S — сумма долга через к лет;
Р — объем предоставленной ссуды;
ik — ставка процента;
nk — продолжительность ссуды в годах, в течение которых применялись данные ставки.
Рассмотрим условный пример.
Допустим, банком выдана ссуда заемщику в размере Р = 10 000 руб. на 5 лет с уплатой 10% годовых по истечении срока займа. Определить размер задолженности через 5 лет.
S5 = 10 000 х (1 + 0,1) 5 = 16 105 руб. Общая сумма начисленных за 5 лет процентов при указанном способе составит:
S5— P = (16 105 — 10 000) = 6 105 руб.
В случае если бы банк использовал простые проценты и взыскивал их ежегодно, то доход от этой сделки был бы равен:
Psixk = 10 000 X 10% х 5 = 5 000 руб.
Как видим, получено довольно ощутимое отклонение, которое ведет к увеличению чистого дохода банка на 1 105 руб. [6 105 — 5 000].
При начислении процентов несколько раз в году рассмотренная выше формула сложных процентов примет вид :
где m — число начислений процентов в году;
N — общее число периодов начисления процентов.
Банк должен тщательно анализировать все моменты, которые могут в конечном итоге повлиять на прибыльность банковских операций. Например, необходимо учитывать характер инфляции и в этой связи определять, что целесообразней для банка: либо наращивать сумму долга посредством начисленных, но невостребованных процентов, либо получать ежегодную плату за кредит.
Возможны различные способы начисления процента: они определяются характером измерения количества дней пользования ссудой и продолжительностью года в днях (временной базы для расчета процентов).
Так, число дней ссуды может определяться точно или приближенно, когда продолжительность любого полного месяца признается равной 30 дням. Временная база приравнивается либо к фактической продолжительности года (365 или 366 дней) или приближенно к 360 дням. Соответственно, применяют следующие варианты начисления сложных процентов :
1. Точные проценты с фактическим числом дней ссуды; этот способ дает самые точные результаты и применяется многими центральными и крупными коммерческими банками. Он характеризуется тем, что для расчета используется точное число дней ссуды, временная база равняется фактической продолжительности года. Например,
Р — сумма выданного кредита — 100 000 руб.,
i — ставка процента — 9% годовых.
К — точное число дней ссуды,
S — наращенная сумма долга.
S = 100 000 х (1+ 0,09% х 260 дн.: 365 дн;) = 106 411 руб.
2. Обыкновенные проценты с точным числом дней ссуды. В этом случае, так же как и в предыдущем, для расчета берется точное число дней ссуды, но временная база приравнивается к 360 дням. Если срок кредита превышает 360 дней, то сумма начисленных процентов будет больше, чем предусмотрено годовой ставкой (так, если период ссуды равен 364 дням, то 364 : 360 = 1,011). Рассмотрим данный способ на предложенном выше примере:
S2 = 100 000 х (1 + 0,09% х 260 дн. : 360 дн.) = 106 499 pуб.
3. Обыкновенные проценты с приближенным числом дней ссуды.
Здесь продолжительность ссуды в днях определяется приближенно, временная база равна 360 дням. Считается, что точное число дней ссуды в большинстве случаев больше приближенного, поэтому и размер начисленных процентов с точным числом дней обычно больше, чем с приближенным.
В нашем примере приближенное число дней ссуды равно 257 дням (S3), учитывая это:
S3 = 100 000 х (1 + 0,09% х 257 дн. : 360 дн.) = 106 424 руб.
Приведенные расчеты показывают, что второй способ начисления процентов, а именно обыкновенные проценты с точным числом дней ссуды дает несколько больший результат относительно двух других вариантов.
Банковская практика в России предусматривает начисление процентов по привлеченным и размещенным средствам (за исключением долговых обязательств и операций с платежными картами) по первому способу, а именно — как точные проценты с фактическим числом дней ссуды. По векселям и депозитным сертификатам применяется способ начисления обыкновенных процентов с приближенным числом дней ссуды.
В чем заключается различие между точным и приближенным процентом
Контрольные вопросы
1. Что показывает множитель наращения в формуле наращения простыми процентами?
2. Как связаны между собой наращение простыми процентами и арифметическая прогрессия?
3. В чем заключается различие между точным и приближенным процентом?
4. Что показывает множитель дисконтирования в формуле наращения про-стыми процентами?
5. Если простую процентную ставку увеличить в два раза, как изменится наращенная сумма
Задача 1. На какой срок клиент банка может взять кредит в размере 200 тыс.руб. под простые проценты с условием, чтобы величина возврата долга не превышала 220 тыс. руб., если процентная ставка равна 14% годовых, в расчет принимаются точные проценты с точным числом дней и год високосный?
Задача 2. Найдите величину дохода кредитора, если за предоставление в долг на полгода некоторой суммы денег он получил 555 тыс. руб. При этом приме-нялась простая процентная ставка в 22%
Задача 3. Банк выдал ссуду на 45 дней в размере 100 тыс. руб. под простую процентную ставку 12% годовых. Рассчитайте доход банка, если при начисле-нии простых процентов считается, что в году: а) 360 дней; б) 365 дней.
Задача 4. На какой срок необходимо поместить имеющуюся денежную сумму под простую процентную ставку 10% годовых, чтобы начисленные проценты были в 1,5 раза больше первоначальной суммы?
Задача 5. Вам 27 декабря будет нужна сумма 150 тыс. руб. Какую сумму 10 июня этого же года Вы должны положить в банк под простую процентную ставку 12 % годовых, если в расчете применяется обыкновенный процент с точным числом дней?
Задача 6. В финансовом договоре клиента с банком предусмотрено погашение долга в размере 240 тыс. руб. через 150 дней при взятом кредите в 200 тыс. руб. Определите доходность такой сделки для банка в виде годовой процентной ставки. При начислении банк использует простые обыкновенные проценты.
Расчет процентов для краткосрочных ссуд
Обычно к наращению по простым процентам прибегают при выдаче краткосрочных ссуд, т.е. на срок менее одного года. Поскольку ставка, как правило, фиксируется в расчете на год, то при сроке ссуды менее года необходимо определить, какая часть годового процента уплачивается кредитору. Аналогичная проблема возникает и в других случаях, когда срок ссуды меньше периода начисления.
Рассмотрим наиболее распространенный в практике случай – с годовым периодом начисления. Выразим общий срок ссуды в виде дроби
где t– число дней ссуды;
К – число дней в году, или временная база.



При расчете обычно полагают, что К = 360 (12 месяцев по 30 дней) или К = 365, 366 дней. Если К = 360 дней, проценты называются обыкновенными. В этом случае формула (7) примет вид:

При использовании действительной продолжительности года 365(366) получают точные проценты и в этом случае формула (7) примет вид:

Наращенная сумма S в формулах (8) и (9) становится разной в зависимости от особенностей определения t (срока ссуды), срок ссуды можно определить двумя способами:
Точный метод определения количества дней пользования ссудой состоит в следующем. Определяется фактическое число дней между двумя датами – выдачи ссуды (дата перечисления валюты ссуды со счета банка) и возврата долга (датой зачисления средств с учетом процентов на счет банка).
Приближенный метод – t определяется исходя из 30-дневной продолжительности каждого месяца.
При точном и приближенном методе дата выдачи и дата погашения ссуды принимается за один день.
Таким образом, можно выделить три варианта расчета процентов по ссудам сроком до 1 года.
1. Точные проценты с точным числом дней ссуды. Этот вариант дает самые точные результаты. Данный способ применяют центральные банки многих стран (Португалия, США) и крупные коммерческие банки, например в Великобритании. Обычно он обозначается как 365/365 или АСТ/АСТ.
2. Обыкновенные проценты с точным числом дней ссуды. Такой подход, называемый еще банковским, применяется в ссудных операциях коммерческих банков ряда стран: Франция, Бельгия, Испания, Швейцария, Югославия. Особенность этого метода в том, что при сроке ссуды более 360 дней, размер начисленных процентов больше, чем предусмотрено годовой ставкой.


Показатели t и k
| Измерение | t | k |
| Точное | Фактически дней в месяце | Фактически дней в году 365 или 366 |
| Приближенное | Число дней во всех месяцах принимается равным 30 | Продолжительность года 360 дней |
Например, срок ссуды равен 364 дня. Тогда множитель наращения составит:

Этот метод обозначается как 365/360 или АСТ/360 и дает несколько больший результат, чем применение точных процентов.
3. Обыкновенные проценты с приближенным числом дней ссуды. Такой метод применяется тогда, когда не требуется большой точности, например при промежуточных расчетах, а также при частичном погашении ссуды. Он принят в Германии, Дании, Швеции и обозначается как 360/360.
Вариант расчета точных процентов с приближенным числом дней ссуды лишен смысла и не применяется.
Так как точное число дней ссуды в большинстве случаев, но, разумеется, не всегда больше приближенного (в чем легко убедиться, определив среднее за год число дней в месяце, которое равно 30,58), то проценты с точным числом дней обычно дают больший рост.
Разумеется, клиенту и банку необходимо учитывать возможные варианты возврата долга. Так, для заемщика выгоднее вариант сделки по первому варианту, а для банка – по второму (или по третьему).
В Российской Федерации используются как точные, так и приближенные проценты. Совершенствование финансовых расчетов, конкуренция, приводят к тому, что получают распространение сделки, в которых применяются точные проценты.
Между точными и обыкновенными процентами при прочих равных условиях (одинаковой продолжительности ссуды, дохода и исходной суммы) существуют определенные отношения, которые используются для определения последствий выбора временной базы (K) в финансовых вычислениях или для определения эквивалентных (дающих одинаковые результаты) процентных ставок. Эти соотношения имеют вид:
 |
 |
Полученные формулы характеризуют эквивалентность процентных ставок при различной временной базе. Из этих формул вытекает, что, например, 40% годовых при начислении процентов с временной базой 360 дней (обыкновенные проценты) дает тот же финансовый результат, что и ставка i= 40,55% при временной базе 365 дней.
Пример 7.
Акционерное общество (АО) для погашения задолженности по счетам поставщиков считает возможным взять краткосрочный кредит под 40% годовых. Год не високосный. Ссуда 100 млн. руб. планируется с 20 января по 5 марта включительно. Определим возможные варианты возврата долга.
Точное число дней ссуды определяем по таблице 1. Оно равно: 64 – 20 = 44 дн.
Приближенное число дней ссуды равно:
11 дн. января (т.к. число дней принимается равным 30) + 30 дн. (один полный месяц) + 5 дн. марта – 1 = 45 дн.
Возможные варианты возврата долга:
1) по точным процентам с точным числом дней ссуды:
S = 100 (1 + 44/365 · 0,4) = 100 (1 + 0,1205479 · 0,4) = 104,82191 млн. руб.
2) по обыкновенным процентам с точным числом дней ссуды:
S = 100 (1 + 44/360 · 0,4) = 100 (1 + 0,1222222 · 0,4) = 104,88889 млн. руб.
3) по обыкновенным процентам с приближенным числом дней ссуды:
S = 100 (1 + 45/360 · 0,4) = 100 (1 + 0,125 · 0,4) = 105,0 млн. руб.
Вариационный размах наращенных сумм по вариантам ссуды значителен и составляет 180 тыс. руб. Такая разница в вариантах сделки весьма существенна, особенно если предположить, что речь идет об инвалюте.


ОСНОВНЫЕ ПОНЯТИЯ
Кредит в условиях рынка выступает в различных формах. Основными являются коммерческийибанковский кредиты.
Коммерческий кредит связан с продажей товаров и отсрочкой платежа на определенное время. Таким образом, объектом этого кредита являются средства в товарной форме. Кредитным документом является коммерческий вексель. Он представляет собой письменное долговое обязательство, составленное по установленной форме. Вексель предоставляет векселедержателю бесспорное право по истечении срока векселя требовать от должника (векселедателя) указанную в векселе сумму. Векселя бывают простые и переводные.
Простой вексель (соло-вексель) – это обязательство покупателя товара уплатить в указанный срок определенную сумму продавцу. Вексель выписывается покупателем и передается продавцу товара.
Переводной вексель (тратта) представляет собой письменный приказ продавца (трассанта) покупателю (трассату) об уплате обозначенной в векселе суммы в указанный срок третьему лицу (ремитенту). Передаточная надпись на обратной стороне векселя называется индоссамент. С помощью индоссамента вексель может передаваться многократно, по существу являясь денежным документом.
Банковский кредит состоит в предоставлении банками предпринимателям и другим заемщикам денежных кредитов или денежных ссуд. Здесь, в отличие от коммерческого кредита, объектом являются денежные средства. Использование в обращении банковских векселей расширяют масштабы вексельного оборота и делают его более обеспеченным вследствие гарантий, выдаваемых банками. Вексель используется как платежное средство. В случае необходимости получения денег по векселю ранее указанного срока векселедержатель может продать его банку по более низкой цене, т. е. ниже суммы, указанной на векселе. Сумма, указанная на векселе, является его номинальной стоимостью. Такая сделка носит название учета векселя или дисконтирования.
По существу, дисконтирование – это задача, обратная наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. Такая ситуация может возникнуть, например, при разработке условий контракта. Расчет P по S необходим и тогда, когда проценты с суммы S удерживаются вперед, т.е. непосредственно при выдаче ссуды. В этих случаях, говорят, что сумма S дисконтируется или учитывается, сам процесс начисления процентов и их удержание называется учетом, а удержанные проценты (или разница между номинальной стоимостью долгового обязательства и суммой, полученной векселедержателем в результате учета векселя) – дисконтом.

Величину P, найденную с помощью дисконтирования, называют современной величиной суммы S, а иногда, в зависимости от контекста – современной (текущей, капитализированной) стоимостью. Современная величина в сумме денег является одним из важнейших понятий в количественном анализе финансовых операций. В большинстве случаев именно с помощью дисконтирования, а не наращения учитывается такой фактор, как время.
Логика финансовых операций наращения и дисконтирования приведена на рис. 6.
В чем заключается различие между точным и приближенным процентом
Наращение и дисконтирование по простым процентным ставкам.
2.3 Практика наращеня простых процентов
Поскольку процентная ставка как правило, устанавливается в расчете за год, то при сроке ссуды мене года необходимо определить, какая часть годового процента уплачивается кредитору. Аналогичная проблема возникает и в случаях, когда срок ссуды меньше периода начисления.
Рассмотрим наиболее распространенный в практике случай – с годовыми периодами начисления. Очевидно, что срок ссуды необязательно равен целому числу лет. Выразим срок n в виде дроби

В этом случае формула 2.3 примет вид

Существует несколько вариантов расчета процентов различным выбором временной базы и способом измерения срока сделки:“Германская практика” – год делиться на 12 месяцев по 30 дней в каждом ( 
“Французская практика” Продолжительность года – 360 дней, а продолжительность месяца в днях соответствует календарю.
“Английская практика” Продолжительность года – 365 дней, а продолжительность месяца в днях соответствует календарю.
Расчет числа дней сделки может быть точным или приближенным. В первом случае вычисляется фактическое число дней между двумя датами. Во втором случае продолжительность сделки определяется числом с месяцев и дней ссуды, при этом продолжительность всех месяцев полагается равным 30 дням. В обоих случаях дата выдачи и дата погашения считается за 1 день.
Возможны применения на практике три варианта расчета простых процентов.
1. Точные проценты с точным числом дней ссуды. Этот вариант, естественно, дает самые точные результаты. Данный способ применяется центральными банками многих стран и крупными коммерческими банками, например, в Великобритании, США. В коммерческих документах он обозначается как 365/365 или АСТ/АСТ.
Очевидно, что вариант расчета с точными процентами и приближенным числом дней ссуды лишен смысла и не применяется.
Поскольку точное число дней ссуды в большинстве случаев, но разумеется, не всегда. Больше приближенного (в чем легко убедиться, определив среднее за год, число дней в месяце, которое равно 30,58), то метод начисления процентов с точным числом дней ссуды обычно дает больший рост, чем с приближенным.
Между величиной процентного дохода рассчитанного с использованием различной временной базы при равной продолжительности ссуды существует следующее соответствие:
Эти соотношения могут быть использованы при определении эквивалентных ставок, т.е. ставок, приносящих одинаковые процентные доходы при различных временных базах и равных первоначальных капиталов.
Если общий срок ссуды захватывает 2 смежных календарных года и есть необходимость в делении суммы процентов между ними, то общая сумма начисленных простых процентов составит сумму процентов за каждый год (срок)







