В чем заключается суть реактивного движения следствием какого закона оно является
Основные сведения о реактивном движении в природе
Что такое реактивное перемещение
Определение реактивного перемещения.
Реактивное перемещение — это движение тела, которое возникает благодаря отделению некоторой его части (массы) с определенной скоростью относительно него.
В основе реактивного движения лежит закон сохранения импульса.
Закон сохранения импульса — это сумма импульсов всех тел, которые входят в данную замкнутую систему и остаются постоянной при любых взаимодействиях этих тел между собой внутри данной системы.
Данный закон является следствием из второго и третьего законов Ньютона.
Также реактивное движение тесно связано с реактивной тягой.
Реактивная тяга — это такая сила, которая возникает из сопла летательного аппарата в результате истечения газов с определенной скоростью.
Знание закона сохранения импульса позволяет изменять скорость перемещения тела. К примеру, если человек при движении в лодке будет бросать камни в определенную сторону, то движение лодки будет осуществляться в противоположном направлении. В космическом пространстве закон сохранения импульса не пропадает. Для изменения направления движения используют реактивные двигатели.
Формула, описывающая реактивное движение:
Примеры реактивного движения в природе
В природе, в основном, реактивное движение присутствуют у животных, обитающих в водной среде.
Многие морские животные для передвижения используют реактивное движение. Среди этих животных: медузы, осьминоги, морские гребешки, кальмары, сальпы, каракатицы. Все эти животные используют реакцию выбрасываемой струи воды.
В качестве примера можно рассмотреть каракатиц и осьминогов. Они забирают воду в жаберную полость, а затем выбрасывают энергично струю воды через воронку. Каракатица направляет трубку воронки назад или в бок и, выдавливая из нее воду, может быстро двигаться в разные стороны. Осьминоги придают своему телу обтекаемую форму, благодаря складыванию щупальцев над головой, и могут таким образов управлять своим движением.
Большинство медуз пользуются реактивным способом движения, выталкивая воду из полости своего зонтика.
Некоторые представители насекомых также используют для перемещения реактивное движение. Так, например, длиннобрюхие личинки стрекоз используют реактивное движение в минуту опасности. Данные личинки используют свою заднюю кишку. Они наполняют ее водой, затем силой выбрасывают воду. Тем самым личинка перемещается по принципу реактивного движения.
Физические основы реактивного движения
В основы реактивного движения входит рассмотрение закона сохранения импульса. При реактивном движении появляется реактивная сила, толкающее тело.
Особенность реактивного движения заключается в том, что в результате взаимодействия между собой частей системы, в ней возникает движение без какого-либо взаимодействия с внешними телами.
Сила, сообщая ускорение телу, возникает за счет взаимодействия этих тел с землей, воздухом или водой.
Движение тела можно получить, например, с помощью вытекания струи жидкости или газа.
Реактивное движение в технике используется в автомобилестроении, в речном транспорте, в военном деле, в космонавтике и авиации.
Закон сохранения импульса. Реактивное движение
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.
Рассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через 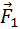
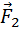
Если эти тела взаимодействуют в течение времени t, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны:
Применим к этим телам второй закон Ньютона:
Где 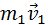
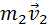
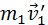
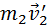
Закон сохранения импульса:
Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему.
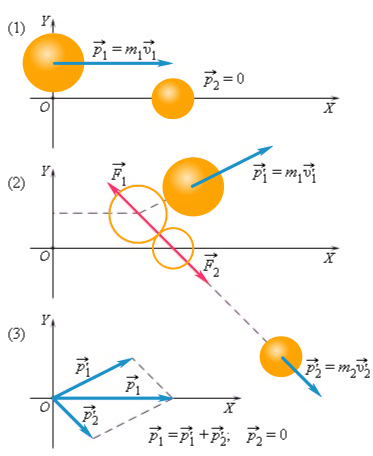
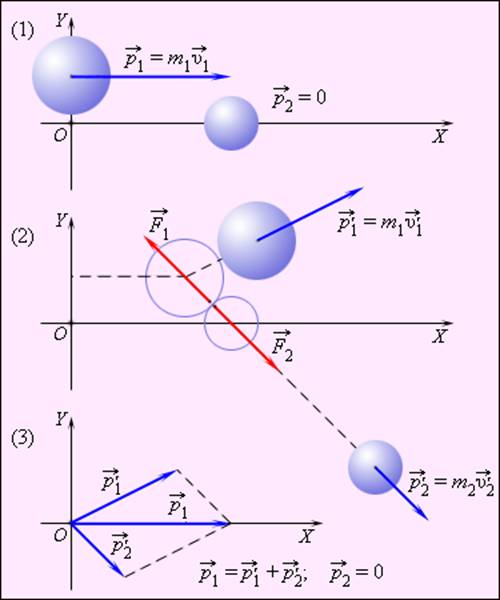
Рис. 1.17.1 иллюстрирует закон сохранения импульса на примере нецентрального соударения двух шаров разных масс, один из которых до соударения находился в состоянии покоя.
Нецентральное соударение шаров разных масс: 1 – импульсы до соударения; 2 – импульсы после соударения; 3 – диаграмма импульсов
Изображенные на рис. 1.17.1 вектора импульсов шаров до и после соударения можно спроектировать на координатные оси OX и OY. Закон сохранения импульса выполняется и для проекций векторов на каждую ось. В частности, из диаграммы импульсов (рис. 1.17.1) следует, что проекции векторов 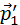
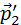
Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.
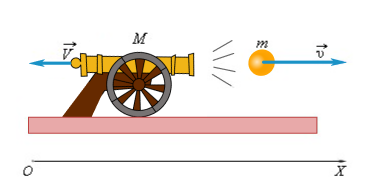
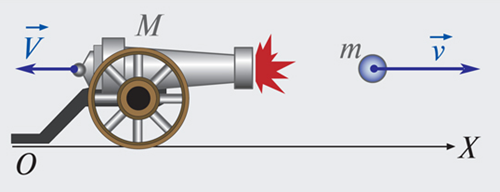
Отдача при выстреле из орудия
На принципе отдачи основано реактивное движение. В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью 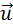
где V – скорость ракеты после истечения газов. В данном случае предполагается, что начальная скорость ракеты равнялась нулю.
Полученная формула для скорости ракеты справедлива лишь при условии, что вся масса сгоревшего топлива выбрасывается из ракеты одновременно. На самом деле истечение происходит постепенно в течение всего времени ускоренного движения ракеты. Каждая последующая порция газа выбрасывается из ракеты, которая уже приобрела некоторую скорость.
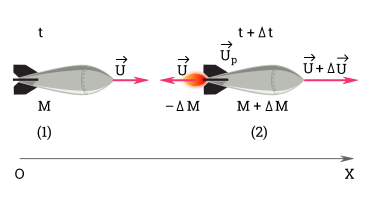
Для получения точной формулы процесс истечения газа из сопла ракеты нужно рассмотреть более детально. Пусть ракета в момент времени t имеет массу M и движется со скоростью 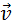
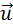
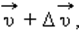
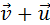
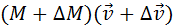
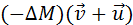
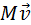
Величиной 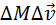
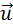
Величина 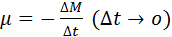
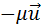
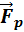
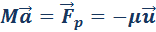
где u – модуль относительной скорости. С помощью математической операции интегрирования из этого соотношения можно получить формулу Циолковского для конечной скорости υ ракеты:
где 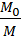
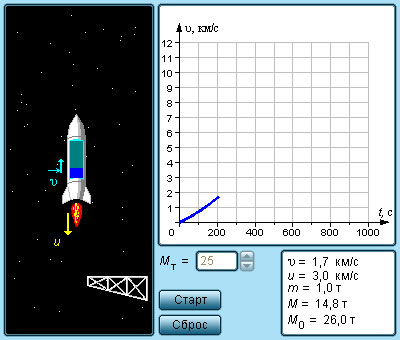
Из нее следует, что конечная скорость ракеты может превышать относительную скорость истечения газов. Следовательно, ракета может быть разогнана до больших скоростей, необходимых для космических полетов. Но это может быть достигнуто только путем расхода значительной массы топлива, составляющей большую долю первоначальной массы ракеты. Например, для достижения первой космической скорости υ = υ1 = 7,9·10 3 м/с при u = 3·10 3 м/с (скорости истечения газов при сгорании топлива бывают порядка 2–4 км/с) стартовая масса одноступенчатой ракеты должна примерно в 14 раз превышать конечную массу. Для достижения конечной скорости υ = 4u отношение 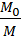
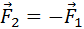
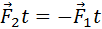
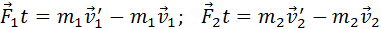
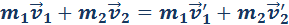
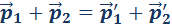
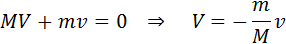
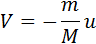
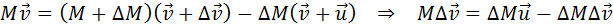
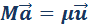
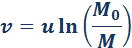



 — это реактивная сила.
— это реактивная сила.