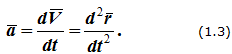В чем заключается векторный способ задания движения точки

Векторный способ задания движения точки

Введение

Связь векторного способа задания движения с координатным осуществляется по формуле:
,
где – единичные векторы (орты) в направлении осей выбранной системы координат.

Основные формулы при векторном способе задания движения

Скорость точки

Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы приводим основные результаты этой теории в векторном виде.

Итак, нам задана зависимость радиус-вектора материальной точки M от времени :
.

Дифференцируя радиус-вектор по времени, мы находим вектор скорости точки:
.
Модуль вектора скорости:
,
где в круглых скобках обозначено скалярное произведение векторов.

Единичный вектор в направлении касательной к траектории:
.

Ускорение точки

Дифференцируя вектор скорости по времени, находим вектор ускорения точки:
.
Модуль вектора ускорения:
.

Разложим вектор ускорения на две взаимно перпендикулярные компоненты: – параллельную касательной к траектории; и – перпендикулярную к ней.
.
Компонента называется касательным, или тангенциальным ускорением, а компонента – нормальным ускорением.

Тангенциальное ускорение

Нормальное ускорение

Радиус кривизны траектории:
.
Центр кривизны траектории:
.

Единичный вектор в направлении бинормали:
.

Источник

iSopromat.ru

Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.

Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.

В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.

Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Векторный способ задания движения точки

Средней скоростью называется физическая величина равная отношению изменения координаты точки к интервалу времени, в течение которого это изменение произошло.

Векторный способ задания движения точки

В этом случае положение точки на плоскости или в пространстве определяется вектором-функцией

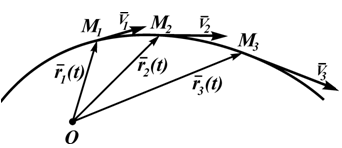
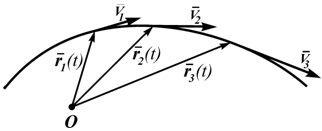
Годограф r, т.е. положение концов этого вектора в пространстве, определяет траекторию движущейся точки. Ее скорость в этом случае определяется как производная от радиуса-вектора и направлена по касательной к годографу r (по касательной к траектории движения точки, рисунок 1.1):

V=dr/dt (1.2)

Этот вектор откладывается от неподвижной точки, выбранной за начало отсчета, его конец определяет положение движущейся точки.

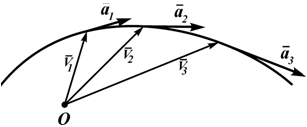
Ускорение точки (изменение ее скорости) определяется как производная от скорости:

Вектор ускорения направлен по касательной к годографу вектора скорости (рисунок 1.2, б).

Источник

В чем заключается векторный способ задания движения точки

Движение. Виды движений. Описание движения. Система отсчета.

Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.

А) Равномерное прямолинейное движение материальной точки.

Б) Равноускоренное прямолинейное движение материальной точки.

В) Движение тела по дуге окружности с постоянной по модулю скоростью.

Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.

1. Векторный способ описания движения

ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.

Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.

При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.

В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.

2. Координатный способ описания движения

ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.

В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.

Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )

Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: r_x = x , r_y = y , r_z = z .

3. Естественный способ описания движения

ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.

Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.

Источник

Способы задания движения точки (векторный способ)

При данном способе задания движения положение точки на плоскости или в пространстве определяется вектором-функцией

r = r(t) (1.1)

Этот вектор откладывается от неподвижной точки, выбранной за начало отсчета, его конец определяет положение движущейся точки.

Годограф r, т.е. положение концов этого вектора в пространстве, определяет траекторию движущейся точки. Ее скорость в этом случае определяется как производная от радиуса-вектора и направлена по касательной к годографу r (по касательной к траектории движения точки, рисунок 1.1):

V = dr/dt (1.2)

Ускорение точки (изменение ее скорости) определяется как производная от скорости:

Вектор ускорения направлен по касательной к годографу вектора скорости (рисунок 1.2, б).

Вектор скорости точки.

Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки. Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится в момент времени t в положении М, определяемом радиусом-вектором , а в момент t₁ приходит в положение M_l, определяемое вектором . Тогда перемещение точки за промежуток времени определяется вектором , который будем называть вектором перемещения точки. Этот вектор направлен по хорде, если точка движется криволинейно (рис. 4, а), и вдоль самой траектории АВ, когда движение является прямолинейным (рис. 4, б).

Из треугольника ОМ M₁ видно, что , следовательно, .

Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростьюточки за промежуток времени Δt:

Направлен вектор так же, как и вектор , т. е. при криволинейном движении вдоль хорды ММ₁ в сторону движения точки, а при прямолинейном движении — вдоль самой траектории (от деления на Δt направление вектора не изменяется).

Очевидно, что чем меньше будет промежуток времени Δt, для которого вычислена средняя скорость, тем велича будет точнее характеризовать движение точки. Чтобы получить точную характеристику движения, вводят понятие о скорости точки в данный момент времени.

Скоростью точки в данный момент времени t называется векторная величина , к которой стремится средняя скорость при стремлении промежутка времени Δt к нулю:

Предел отношения при представляет собой первую производную от вектора по аргументу t и обозначается, как и производная от скалярной функции, символом dr̅/dt. Окончательно получаем

Так как предельным направлением секущей ММ₁ является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.

Формула (8) показывает также, что вектор скорости v ̅ равен ототношению элементарного перемещения точки dr ̅, направленного по касательной к траектории, к соответствующему промежутку времени dt.

При прямолинейном движении вектор скорости v ̅ все время направлен вдоль прямой, по которой движется точка, и может изменяться лишь численно; при криволинейном движении кроме числового значения все время изменяется и направление вектора скорости точки. Размерность скорости L/T, т. е. длина/время; качестве единиц измерения применяют обычно м/с или км/ч. Вопрос об определении модуля скорости будет рассмотрен в позже.

Вектор ускорения точки

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.

В СИ единицей ускорения является метр на секунду в квадрате .

Пусть в некоторый момент времени t движущаяся точка находится в положении М и имеет скорость v, а в момент t₁ приходит в положение M₁ и имеет скорость v₁ (рис. 8).

Рис.8

Тогда за промежуток времени ∆t=t₁-t скорость точки получает приращение . Для построения вектора отложим от точки М вектор, равный v₁, и построим параллелограмм, в котором диагональю будет , a одной из сторон . Тогда, очевидно, вторая сторона и будет изображать вектор . Заметим, что вектор всегда направлен в сторону вог­нутости траектории.

Отношение приращения вектора скорости к соответствующему про­межутку времени ∆t определяет век­тор среднего ускорения точки за этот промежуток времени:

Вектор среднего ускорения имеет то же направление, что и век­тор , т.е. направлен в сторону вогнутости траектории.

Ускорением точки в данный момент времени t называется век­торная величина , к которой стремится среднее ускорение при стремлении промежутка времени ∆t к нулю: Вектор ускорения точки в данный момент време­ни равен первой производной от вектора скорости или второй произ­водной отрадиуса-вектора точки по времени.

Найдем, как располагается вектор по отношению к траекто­рии точки. При прямолинейном движении вектор направлен вдоль прямой, по которойдвижется точка.

При прямолинейном движении с возрастающей по модулю скоростью (рис. 9, а) векторы и сонаправлены ( ) и проекция ускорения на направление движения положительна.

При прямолинейном движении с убывающей по модулю скоростью (рис. 9, б) направления векторов и противоположны ( ) и проекция ускорения на направление движения отрицательна.

Рис.9

Если траекторией точки явля­ется плоская кривая, то вектор ускорения , так же как и вектор , лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор на­правлен в сторону вогнутости траектории и лежит в плоскости, про­ходящей через касательную к траектории в точке М и прямую, па­раллельную касательной в соседней точке M₁ (рис. 8). В пределе, когда точка М стремится к М, эта плоскость занимает положение так называемой соприкасающейся плоскости, т.е. плоскости, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки. Следовательно, в общем случае вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.

Дата добавления: 2019-02-22 ; просмотров: 202 ; Мы поможем в написании вашей работы!

Источник