Особенности стандартов, описывающих мощность в звукотехнике

Многим иногда приходилось задумываться, что же именно обозначает мощность, в том или ином виде приводимая в паспортах акустических систем и звукоусилительной аппаратуры. Материалов на эту тему в сети и печатных изданиях встречается на удивление мало, внятных ответов на вопросы тоже.

Попытаюсь хоть как-то уменьшить число белых пятен в этой области. Некоторые, более точные описания определений возникли у меня в диалоге, при попытке лучше объяснить собеседнику их смысл. Часть своих определений я попросту вытащил из конференции, где многократно уже пытался дать доступные ответы на подобные вопросы, попутно шлифуя тексты своих ответов.

Международные стандарты

RMS (Root Mean Squared) — среднеквадратичное значение мощности, ограниченной заданными нелинейными искажениями.

Мощность замеряется синусоидальным сигналом на частоте 1 кГц при достижении 10% THD. Она вычисляется, как произведение среднеквадратичных значений напряжения и тока при эквивалентном количестве теплоты, создаваемой постоянным током. То есть, эта мощность численно равна квадратному корню из произведения квадратов усредненных величин напряжения и тока.

Для синусоидального сигнала среднеквадратичное значение меньше амплитудного в V2 раз (× 0,707). Вообще же, это виртуальная величина, термин «среднеквадратичный», строго говоря, может быть применен к напряжению или силе тока, но не к мощности. Известный аналог — действующее значение (все знают его для сети электропитания переменным током — это те самые 220 В для России).

Таким образом, стандарт RMS был одной из не самых удачных попыток описать параметры звуковой аппаратуры, которые не отражают громкость, как величину.

В усилителях и акустике этот параметр тоже, по сути, имеет весьма ограниченное применение — усилитель, который выдает 10% искажений не на максимальной мощности (когда возникает клиппинг, ограничение амплитуды усиливаемого сигнала с возникающими специфическими динамическими искажениями), еще поискать. До достижения максимальной мощности искажения транзисторных усилителей, например, не превышают зачастую сотых долей процента, а уж выше резко возрастают (нештатный режим). Многие акустические системы при длительной работе с таким уровнем искажений уже способны выйти из строя.

Для совсем уж дешевой техники указывается другая величина — PMPO, совсем уж бессмысленный и никем не нормированный параметр, а значит, друзья-китайцы измеряют его так, как бог на душу положит. Если точнее, в попугаях, причем каждый в своих. Значения PMPO часто превышают номинальные вплоть до коэффициента 20.

PMPO (Peak Music Power Output) — пиковая кратковременная музыкальная мощность, величина, которая означает максимально достижимое пиковое значение сигнала независимо от искажений вообще за минимальный промежуток времени (обычно за 10 mS, но, вообще, не нормировано).

Как следует из описания, параметр еще более виртуальный и бессмысленный в практическом применении. Посоветую эти значения не воспринимать всерьез и на них не ориентироваться. Если вас угораздило покупать аппаратуру с параметрами мощности, указанными только, как PMPO, то единственный совет — послушать самостоятельно и определить, подходит это вам или нет.

DIN 45500 — комплекс общепринятых стандартов IEEE, описывающих различные звукоусилительные характеристики аппаратуры более достоверным образом.

DIN POWER — значение выдаваемой на реальной нагрузке (для усилителя) или подводимой (к АС) мощности, ограниченной нелинейными искажениями.

Измеряется подачей сигнала с частотой 1 кГц на вход устройства в течение 10 минут. Мощность замеряется при достижении 1 % THD (нелинейных искажений).

Строго говоря, есть и другие виды измерений, например, DIN MUSIC POWER, описывающая мощность уже музыкального сигнала. Обычно указываемая величина DIN music выше, чем приводимая как DIN.

Информации по данному стандарту у меня немного, привожу только то, что удалось собрать.

Отечественные стандарты

Иногда это приводило к парадоксам — при искажениях типа «ступенька», возникающих в усилителях класса АВ на малых уровнях громкости, уровень искажений мог снижаться при увеличении выходной мощности сигнала до номинальной. Таким образом достигались рекордные номинальные характеристики в паспортах усилителей, с крайне низким уровнем искажений при высокой номинальной мощности усилителя. Тогда как наивысшая статистическая плотность музыкального сигнала лежит в диапазоне амплитуд 5–15% от максимальной мощности усилителя. Вероятно, поэтому российские усилители заметно проигрывали на слух западным, у которых оптимум искажений мог быть на средних уровнях громкости, тогда как в СССР шла гонка за минимумом гармонических и иногда интермодуляционных искажений любой ценой на одном, номинальном (почти максимальном) уровне мощности.

Максимальная долговременная мощность определяется нарушением тепловой прочности громкоговорителей АС (сползанием витков звуковой катушки и др.).

Общая терминология

Розовый шум (используемый в этих испытаниях) — группа сигналов со случайным характером и равномерной спектральной плотностью распределения по частотам, убывающей с увеличением частоты со спадом 3 дБ на октаву во всем диапазоне измерений, с зависимостью среднего уровня от частоты в виде 1/f. Розовый шум имеет постоянную (по времени) энергию на любом из участков частотной полосы.

Белый шум — группа сигналов со случайным характером и равномерной и постоянной спектральной плотностью распределения по частотам. Белый шум имеет одинаковую энергию на любом из участков частот.

Октава. Музыкальная полоса частот, соотношение крайних частот которой равно 2.

Электрическая мощность. Мощность, рассеиваемая на омическом эквивалентном сопротивлении, равном по величине номинальному электрическому сопротивлению АС, при напряжении, равном напряжению на зажимах АС. То есть, на сопротивлении, эмулирующем реальную нагрузку в тех же условиях.

Источник

Параметры переменного напряжения

Как вы помните из предыдущей статьи, переменное напряжение — это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.

Среднее значение напряжения

Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.

Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком «минус». А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.

То же самое касается и других сигналов, например, двухполярного меандра. Меандр — это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.

Средневыпрямленное значение напряжения

Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая «пробивает пол» берут не с отрицательным знаком, а с положительным.

средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.

На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:

Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:

Среднеквадратичное значение напряжения

Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже простым графиком не отделаешься. Среднеквадратичное значение — это значение постоянного напряжения, который, проходя через нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение обозначается так: RMS (rms) — root mean square.

Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды K_a:

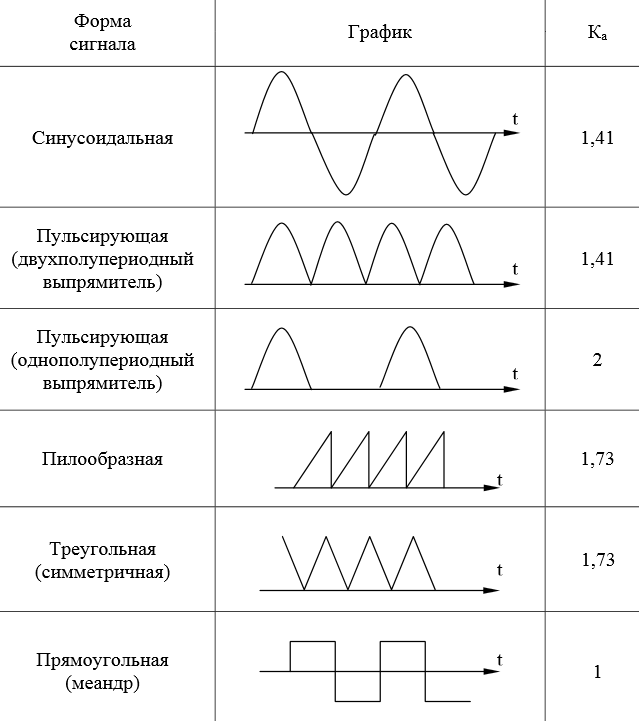
Вот некоторые значения коэффициента амплитуды K_a для некоторых сигналов переменного напряжения:

Более точные значения 1,41 и 1,73 — это √2 и √3 соответственно.

Как измерить среднеквадратичное значение напряжения

Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS — как вы уже знаете — это среднеквадратическое значение. А что за буква «T» впереди? Думаю, вы помните, как раньше была мода на одно словечко: «тру». «Она вся такая тру…», «Ты тру или не тру?» и тд. Тру (true) — с англ. правильный, верный.

Так вот, T-RMS расшифровывается как True RMS — «правильное среднеквадратическое значение». Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип «T-RMS».

мультиметр с True RMS

Проведем небольшой опыт. Давайте соберем вот такую схемку:

Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц

генератор частоты

А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

треугольный сигнал

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?

Так как один квадратик у нас равняется 1 Вольт (мы это видим внизу осциллограммы в красной рамке), то получается, что амплитуда Umax этого треугольного сигнала равняется 4 Вольта. Для того, чтобы рассчитать среднеквадратическое напряжение, мы воспользуемся формулой:

Итак, смотрим нашу табличку и находим интересующий нас сигнал:

Для нас не важно, пробивает ли сигнал «пол» или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды K_a= 1,73.

Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала

Проверяем нашим прибором, так ли оно на самом деле?

Супер! И в правду Тrue RMS.

Замеряем это же самое напряжение с помощью моего китайского мультиметра

Он меня обманул :-(. Он умеет измерять только среднеквадратическое значение синусоидального сигнала, а у нас сигнал треугольный.

Самый интересный сигнал в плане расчетов — это двуполярный меандр, ну тот есть тот, который «пробивает пол».

Его амплитудное Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.

Вот вам небольшая картинка, чтобы не путаться

Так что же все-таки показывает мультиметр при измерении переменного напряжения? Показывает он НЕ амплитудное, НЕ среднее и НЕ среднее выпрямленное напряжение, а среднее квадратическое, то есть действующее напряжение! Об этом всегда помним.

Источник

Важность использования RMS измерений для описания факторов, влияющих на качество электрической энергии

Каждый из нас слышал, что занятие письмом под шум прибоя может оказывать лечебный эффект.

Морские волны подобны синусоидальной волне переменного напряжения, которая используется в качестве эталонной при при определении качества питания. Отклонения от чисто синусоидальной формы волны могут быть обусловлены гармоническими составляющими, некратными гармониками, а также импульсными или колебательными переходными процессами. Изменения амплитуды синусоидального сигнала можно классифицировать следующим образом: падения, всплески и продолжительное перенапряжение либо пониженное напряжение. В то время как изменения в частоте питающего напряжения сравнительно редки и возникают при серьезных неполадках оборудования, чаще имеет место сдвиг фаз при провалах и всплесках. Для того чтобы охарактеризовать или описать синусоидальный сигнал, находящийся под воздействием описанных факторов, влияющих на качество электроэнергии, используются измерения истинных среднеквадратичных значений (Root Mean Squared — RMS). Являющиеся полезными во многих ситуациях, в ряде случаев такие измерения могут оказаться неадекватными либо вводить в заблуждение.

Что же представляют собой RMS?

Среднеквадратичные значения получаются в результате математической процедуры, используемой для расчета единичного значения по последовательности отсчетов. Это позволяет сравнивать один цикл с другим, или одну фазу с другой. RMS-напряжение является эффективным значением изменяющегося или переменного напряжения. Это значение должно соответствовать такой же мощности, как и в случае постоянного напряжения, приложенного к чистому сопротивлению. В нынешнем мире дискретных волновых сигналов, вырабатываемых кристаллами процессоров цифровой обработки сигнала (ЦОС), такие измерения являются одними из наиболее легко реализуемых. Каждое значение данных в течение предопределенного периода (обычно это один цикл) умножается само на себя (возведение в квадрат), а затем все такие значения в течение периода усредняются (суммируются с последующим делением на общее количество) и из полученного значения извлекается квадратный корень.

Для стабильного постоянного сигнала каждый отсчет имеет одно и то же значение, следовательно, любой из них может служить эквивалентом RMS-значения. В случае же синусоидальной волны значения нарастают в пределах первой четверти цикла, затем уменьшаются до нуля и переходят в область отрицательных значений вплоть до минимального значения в пределах второй четверти цикла (см. рис. 1).

Рисунок 1. Форма волны на нагрузке однофазного источника питания с полноволновым измерителем.

RMS-значение чистого синусоидального сигнала составляет примерно 70,7% пикового значения. При искаженной форме волны это не верно, что является ответом на вопрос, почему приборы, измеряющие не в терминах истинных среднеквадратичных значений, могут выдавать совершенно различные результаты при различных степенях искажений и, следовательно, не могут использоваться при наличии гармоник. Те приборы, которые лишь вычисляют 71% от пикового значения будут давать неверный результат для формы тока, показанного на рис. 1. На рисунке изображена классическая форма токового сигнала однофазного источника питания с выпрямлением полной волны, присутствующего во многих электронных устройствах. Эта форма волны с гармоническими искажениями (THD) на уровне 108% имела пиковое значение 3,6 А и истинное среднеквадратичное значение 1,4 А, что не совпадает с рассчитанной величиной 0,707×3,6=2,55 А.

Невысокого качества анализаторы электроэнергии, которые настроены на RMS-значения, могут пропускать некоторые данные. Ряд приборов рассчитывают RMS-значения в ходе нескольких циклов. Весьма вероятно, что эти мониторы не зафиксируют многофазовый провал в течение одного цикла, изображенный на рис. 2.

Рисунок 2. Провал в течение одного цикла в двух фазах.

Такое искажение сигнала типично для случая, когда неполадка устраняется с помощью защитного предохранителя. На рис. 3 провал в течение одного цикла, возникший вследствие пробоя при пиковом напряжении (возможно из-за неисправности изоляции или удара молнии) будет давать различные RMS-значения на каждом из трех циклов.

Рисунок 3. Однофазный провал при пробое пиковым напряжением.

В зависимости от механизма включения триггера и пороговых значений, возможно необнаружение провала вплоть до третьего цикла, поскольку RMS-значение неисправных циклов может превышать порог срабатывания триггера. Неисправность, выражающаяся в сдвиге фаз, может иметь идентичные значения от одного цикла к следующему, несмотря на изменения амплитуды волны. Это происходит, когда используются электроанализаторы со многими механизмами включения триггера, например при переходных процессах или искажениях формы волны. Следует помнить, что хотя прибор не замечает таких неисправностей, это не значит, что они не существуют.

Справка

Консультативно-торговая компания «Энергометрика» поставляет компоненты автоматизации для: АСУ ТП, «интеллектуальное» здание, шкаф электрический, конденсаторная установка, системы учета параметров электроэнергии. SCADA системы.

Источник

Что показывает вольтметр, или математика розетки

О чем эта статья

Сегодня я ненадолго отступлю от своей обычной темы о визуальном программировании контроллеров и обращусь к теме измерений напряжения прямо в ней, в розетке!

Родилась эта статья из дискуссий за чаем, когда разразился спор среди «всезнающих и всеведающих» программистов о том, чего многие из них не понимают, а именно: как измеряется напряжение в розетке, что показывает вольтметр переменного напряжения, чем отличается пиковое и действующие значения напряжений.

Скорее всего, это статья будет интересна тем, кто начинает творить свои устройства. Но, возможно, поможет и кому-то опытному освежить память.

В статье рассказано о том, какие напряжения есть в сети переменного тока, как их измеряют и о том, что следует помнить при проектировании электронных схем.
Всему дано краткое и упрощённое математическое обоснование, чтобы было ясно не только «как», но и «почему».

Кому не интересно читать про интегралы, ГОСТы и фазы — могут сразу переходить к заключению.

Вступление

Когда люди начинают говорить о напряжении в розетке, очень часто стереотип «в розетке 220В» скрывает от их взора реальное положение дел.

Начнем с того, что согласно ГОСТ 29322-2014, сетевое напряжение должно составлять 230В±10% при частоте 50±0,2Гц (межфазное напряжение 400В, напряжение фаза-нейтраль 230В). Но в том же ГОСТ имеется примечание: «Однако системы 220/380 В и 240/415 В до сих пор продолжают применять».

Согласитесь, что это уже совсем не то однозначное «в розетке 220В», к которому мы привыкли. А когда речь начинает идти о «фазном», «линейном», «действующем» и «пиковом» напряжениях — вообще каша получается знатная. Так сколько же вольт в розетке?

Чтобы ответить на этот вопрос начнем с того, как измеряется напряжение в сети переменного тока.

Как измерять переменное напряжение?

Прежде, чем углубиться в дебри цепей переменного тока и напряжения, вспомним школьную физику цепей тока постоянного.

Цепи постоянного тока — вещь простая. Если мы возьмем некоторую активную нагрузку (пусть это будет обычная лампа накаливания, как на рисунке) и воткнем ее в цепь постоянного тока, то все, что происходит в нашей цепи будет характеризоваться всего двумя величинами: напряжением на нагрузке U и током, протекающим через нагрузку I. Мощность, которая потребляется нагрузкой однозначно вычисляется по формуле, известной со школы: .

Или, если учесть, что по закону Ома , то мощность P, потребляемую нагрузкой-лампочкой, можно вычислить по формуле .

С переменным напряжением все куда сложнее: в каждый момент времени — оно может иметь разное мгновенное значение. Следовательно, в разные моменты времени, на нагрузке, подключенной к источнику переменного напряжения (например, на лампе накаливания, воткнутой в розетку) будет выделяться разная мощность. Это очень неудобно с точки зрения описания электрической цепи.

Но нам повезло: форма напряжения в розетке синусоидальная. А синусоида, как известно, полностью описывается тремя параметрами: амплитудой, периодом и фазой. В однофазных сетях (а обычная розетка с двумя дырочками именно и есть однофазная сеть) про фазу можно забыть. На рисунке подробно показаны два периода сетевого однофазного напряжения. Того самого, что в розетке.

Рассмотрим, что означают все эти буковки на рисунке.

Период T — это время между двумя соседними минимумами или соседними максимумами синусоиды. Для осветительной сети РФ этот период составляет 20 миллисекунд, что соответствует частоте 50Гц. Частота колебаний напряжения электрической сети выдерживается очень точно, до долей процента.

Очевидно, что в любых двух точках синусоиды, отстоящих друг от друга на целое число периодов, напряжения всегда равны между собой.

Амплитуда Um — это максимальное напряжение, пик синусоиды. Про действующее напряжение Uд поговорим чуть ниже.

Напряжение в розетке (или однофазной сети) описывается формулой

где t — текущий момент времени, Um — амплитуда (или пиковое значение) напряжения, T — период сетевого напряжения.

Если с однофазным переменным напряжением более или менее все ясно, то попробуем посчитать мощность, которая выделяется на нашей любимой лампе накаливания, при втыкании ее прямо в розетку.

Так как лампа накаливания является активной нагрузкой (а это значит, что ее сопротивление не зависит от частоты напряжения и тока), то мгновенная мощность, выделяемая на лампе накаливания, воткнутой в розетку, будет вычисляться по формуле

где t — текущий момент времени, а R — сопротивление лампы накаливания при нагретой спирали. Зная амплитуду переменного напряжения Um, можно записать:

Понятно, что мгновенная мощность — неудобный параметр, да и на практике не особо нужный. Поэтому практически обычно применяется мощность, усредненная за период.
Именно усредненная мощность указана на лампочках, нагревателях и прочих бытовых утюгах.

Рассчитывается усредненная мощность в общем случае по формуле:

А для нашей синусоиды — по гораздо более простой формуле:

Можете сами подставить вместо функцию и взять интеграл, если не верите.

Не думайте, что про мощность я вспомнил просто так, из вредности. Сейчас поймете, зачем она нам была нужна. Переходим к следующему вопросу.

Что же показывает вольтметр?

Для цепей постоянного тока, тут все однозначно — вольтметр показывает единственное напряжение между двумя контактами.

С цепями переменного тока все опять сложнее. Некоторые (и этих некоторых не так мало, как я убедился) считают, что вольтметр показывает пиковое значение напряжения Um, но это не так!

На самом деле, вольтметры обычно показывают действующее или эффективное, оно же среднеквадратичное, напряжение в сети Uд.

Разумеется, речь идет о вольтметрах переменного напряжения! Поэтому, если будете измерять вольтметром напряжение сети, обязательно убедитесь, что он находится в режиме измерения переменного напряжения.

Оговорюсь, что «пиковые вольтметры», показывающие амплитудные значения напряжения, тоже существуют, но на практике при измерении напряжения питающей сети в быту обычно не применяются.

Разберемся, почему такие сложности. Почему бы не измерять просто амплитуду? Зачем выдумали какое-то «действующее значение» напряжения?

А все дело в потребляемой мощности. Я ведь не просто так писал о ней. Дело в том, что действующее (эффективное) значение переменного напряжения равно величине такого постоянного напряжения, которое за время, равное одному периоду этого переменного напряжения, произведет такую же работу, что и рассматриваемое переменное напряжение.

Или, по-простому, лампочка накаливания будет светить одинаково ярко, воткнем ли мы ее в сеть постоянного напряжения 220В или в цепь переменного тока с действующим значением напряжения 220В.

Для тех, кто уже знаком с интегралами или еще не забыл математику, приведу общую формулу расчета действующего напряжения произвольной формы:

Из этой формулы также становится ясно, почему действующее (эффективное) значение переменного напряжения также называют «среднеквадратичным».

Заметим, что подкоренное выражение и есть та самая «усредненная за период мощность», стоит только поделить это выражение на сопротивление нагрузки R.

Применительно к синусоидальной форме напряжения, страшный интеграл после несложных преобразований превратится в простую формулу:

где Uд — действующее или среднеквадратичное значение напряжение (то самое, которое обычно показывает вольтметр), а Um — амплитудное значение.

Действующее напряжение хорошо тем, что для активной нагрузки, расчет усредненной мощности полностью совпадает с расчетом мощности на постоянном токе:

Это и не удивительно, если вспомнить определение действующего значения напряжения, которое было дано чуть выше.

Ну и, наконец, посчитаем, чему же равна амплитуда напряжения в розетке «на 220В«:

В худшем случае, если у вас сеть на 240В, да еще и с допуском +10%, амплитуда будет аж !

Поэтому, если хотите, чтобы ваши устройства, питающиеся от сети, работали стабильно и не сгорали, выбирайте элементы, которые выдерживают пиковые напряжения не менее 400В. Разумеется, речь идет об элементах, на которые непосредственно подаётся сетевое напряжение.

Отмечу, что для не-синусоидальной формы сигнала действующее значение напряжения рассчитывается по иным формулам. Кому интересно — могут сами взять интегралы или обратиться к справочникам. Нас же интересует питающая сеть, а там всегда должна быть синусоида.

Фазы, фазы, фазы…

Помимо обычной однофазной осветительной сети

220В все слышали и о трехфазной сети

380В. Что такое 380В? А это межфазное эффективное напряжение.

Помните, я сказал, что в однофазной сети про фазу синусоиды можно забыть? Так вот, в трехфазной сети этого делать нельзя!

Если говорить по простому, то фаза — это сдвиг во времени одной синусоиды относительно другой. В однофазной сети мы всегда могли принять за начало отсчета любой момент времени — на расчеты это не влияло. В трехфазной сети необходимо учитывать насколько одна синусоида отстоит от другой. В трехфазных сетях переменного тока каждая из фаз отстоит от другой на треть периода или на 120 градусов. Напомню, что период измеряется также в градусах и полный период равен 360 градусов.

Если мы возьмем осциллограф с тремя лучами и прицепимся к трем фазам и одному нулю, то увидим такую картину.

«Синяя» фаза — начинается от нуля отсчета. «Красная» фаза — на треть периода (120 градусов) позже. И, наконец «зеленая» фаза начинается на две трети периода (240 градусов) позже «синей». Все фазы абсолютно симметричны друг относительно друга.

Какую именно фазу брать за точку отсчета — не важно. Картина будет одинаковой.

Математически можно записать уравнения всех трех фаз:

«Синяя» фаза:

«Красная» фаза:

«Зеленая» фаза:

Если измерить напряжение между любой из фаз и нулем в трехфазной сети — то получим обычные 220В (или 230В или 240В — как повезет, см. ГОСТ).

А если измерить напряжение между двумя фазами — то получим 380В (или 400В или 415В — не забываем об этом).

То есть трехфазная сеть — многолика. Ее можно использовать как три однофазные сети с напряжением 220В или как одну трехфазную сеть с напряжением 380В.

Откуда взялось 380В? А вот откуда.

Если мы подставим в формулу расчета действующего напряжения наши данные о двух любых фазах, то получим:

Uдф — действующее межфазное, оно же линейное напряжение.

Учитывая, что амплитуда каждой фазы получим, чтодля межфазного напряжения. На рисунке наглядно показано, как образуется межфазное напряжение, которое обозначено F1-F2 из двух фазных напряжений фаз F1 и F2. Напряжение фаз F1 и F2 измеряется относительно нулевого провода. Линейное напряжение F1-F2 измеряется между двумя разными фазными проводами.

Как видим, что действующее межфазное напряжение больше амплитуды синусоидального напряжения одной фазы.

Амплитуда межфазного напряжения составляет:

Для наихудшего случая (сеть 240В и межфазное напряжение 415В, да еще 10% сверху) амплитуда межфазного напряжения составит:

Учтите это при работе в трехфазных сетях и выбирайте элементы, рассчитанные не менее, чем на 650В, если им предстоит работать между двумя фазами!

Надеюсь, теперь понятно что показывает вольтметр переменного тока?

Заключение

Итак, очень кратко, почти на пальцах, мы ознакомились с тем какие напряжения действуют в бытовых сетях переменного тока. Подведем краткие итоги всего, изложенного выше.

Источник