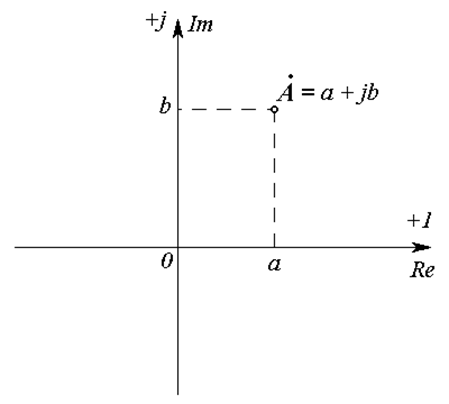X с волной вверху что это
X с чертой наверху символ
Помимо использования разных видов форматирования текста таких как: изменение шрифта, применение полужирного или курсивного начертания, иногда необходимо сделать верхнее подчеркивание в Ворде. Расположить черту над буквой довольно просто, рассмотрим несколько способов решения данной задачи.
С помощью «Диакритических знаков»
Благодаря панели символов сделать черточку сверху можно следующим образом. Установите курсор мыши в нужном месте по тексту. Перейдите во вкладку «Вставка» далее найдите и нажмите в области «Символы» на кнопку «Формула» и выберите из выпадающего меню «Вставить новую формулу».
Откроется дополнительная вкладка «Работа с формулами» или «Конструктор». Из представленных вариантов в области «Структуры» выберите «Диакритические знаки» и кликните по окну с названием «Черта».
В добавленном окне напечатайте необходимое слово или букву.
В результате получится такой вид.
Подчеркивание сверху посредством фигуры
Используя фигуры в Ворде, можно подчеркнуть слово как сверху, так и снизу. Рассмотрим верхнее подчеркивание. Изначально необходимо напечатать нужный текст. Далее перейти во вкладку «Вставка» в области «Иллюстрации» выбрать кнопку «Фигуры». В новом окне кликнуть по фигуре «Линия».
Поставить крестик над словом в начале, нажать и протянуть линию до конца слова, двигая вверх или вниз выровнять линию и отпустить.
Можно изменить цвет верхнего подчеркивания, нужно нажать по линии и открыть вкладку «Формат». Нажав по кнопке «Контур фигуры» указать нужный цвет. Также можно изменить вид подчеркивания и толщину. Для этого перейдите в подпункт ниже «Толщина» или «Штрихи».
В соответствии с настройками палочку можно преобразовать в штрихпунктирную линию, либо изменить на стрелку, в нужном направлении.
Благодаря таким простым вариантам, поставить черту над буквой или цифрой не займёт много времени. Стоит лишь выбрать наиболее подходящий способ из вышепредставленных.
Сре́днее арифмети́ческое (в математике и статистике) множества чисел — число, равное сумме всех чисел множества, делённой на их количество. Является одной из наиболее распространённых мер центральной тенденции.
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
При стремлении количества элементов множества чисел стационарного случайного процесса к бесконечности среднее арифметическое стремится к математическому ожиданию случайной величины.
Содержание
Введение [ править | править код ]
Обозначим множество чисел X = (x1, x2, …, xn), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной ( x ¯ >> 
Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E есть математическое ожидание этой выборки.
На практике разница между μ и x ¯ >> 

Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Примеры [ править | править код ]
Непрерывная случайная величина [ править | править код ]
Если существует интеграл от некоторой функции f ( x ) 

Некоторые проблемы применения среднего [ править | править код ]
Отсутствие робастности [ править | править код ]
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент [ править | править код ]
Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только около 8,16653826392 % ≈ 8,2 %.
Направления [ править | править код ]
При расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 1 ∘ + 359 ∘ 2 = +359^ > >=> 
Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360°==0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).
Здесь легко и интересно общаться. Присоединяйся!
в ворде набирай код – маркер перед знаком.
знак у, код 035F,Alt+X : результат ͟y снизу
k, 035E,Alt+X ; результат ͞k – сверху.
В символах есть коды. и волнистых, и прочих…: )
если в ворде то вставить символ или надстрочным шрифтом (в свойствах шривта поставить галочку надстрочныу и в нужном месте поставить черточку)
В ворде есть переход в формулы жми:
ВСТАВКА – ФОРМУЛЫ – ДИАКРИТИЧЕСКИЕ ЗНАКИ и выбирай знак, в квадратике пиши переменную.
А так есть мастера формул. Международный – это MathType. В нём можно сделать всё, только язык надо зхнать : TeX
Разбираемся в физике частиц: 3) волны, классический вид
Разобравшись с уравнениями для колебаний – описывающими практически всё, что скачет, вибрирует, катается вперёд-назад, как шар на пружине – можно переходить к настолько же распространённому явлению природы, волнам. Волны есть везде: звук и свет, землетрясения, рябь на поверхности пруда, и т.п.
Но перед этим предупреждаю, что термин «волна» может вводить в заблуждение, поскольку в физике он означает не то же самое, что в английском языке. В физике он не означает того, что мы обычно могли бы назвать волной на краю океана – один гребень и одна впадина. В физике волны – это последовательность волн, несколько гребней и впадин, совместно движущихся в одном направлении. У волны простейшего вида все гребни одинаковой высоты и отстоят друг от друга на одно расстояние. Мы будем рассматривать именно такой случай.
Волны – выдающееся явление, если задуматься. Представьте, что вы с другом взяли длинную верёвку и туго натянули её в комнате (рис. 2). Затем представьте, что ваш друг поболтал несколько раз вверх и вниз одним концом верёвки (зелёным). На его конце верёвки появится волна, и она пройдёт по комнате к вашему концу верёвки (красному).
Это удивительно. Я имею в виду – на самом деле поразительно, сильно и критически важно для всего в нашей Вселенной, включая и вас лично. Посмотрите, что произошло. Ни один физический объект слева направо не перемещался – до того, как ваш друг начал двигать конец верёвки, она была протянута через комнату, а в конце, после того, как ваш конец верёвки закончит колебаться и волна пропадёт, верёвка так и останется натянутой через всю комнату, как и было. И всё-таки! Энергия и информация переместились по комнате. Волна в пути переносит энергию, потраченную вашим другом на колебания верёвки – и несёт в своей форме информацию о том, сколько раз и как быстро он её дёргал – к вам, где она заставляет трястись уже вашу руку. И в этом случае она даже тряханёт вашу руку именно столько раз и именно в такой последовательности. Вот это да! Ни один физический объект не перемещался через комнату, а энергия и информация – переместились.
Или, подождите. А не должны ли мы рассматривать волну, как физический объект? Такой же физический, как сама верёвка?
Помня этот глубочайший вопрос, обратимся к небольшому количеству математических формул, необходимых для описания внешнего вида и поведения волны, а затем используем чуть больше математики, чтобы записать уравнения, решениями которых будут волны. Это похоже на то, что мы делали для классического шара на пружине.
Формула для бесконечной волны в определённый момент времени
Эта серия статей сразу после шара на пружине переходит к волнам потому, что волна – это разновидность двойного осциллятора. Она колеблется как во времени, так и в пространстве. Время мы обозначим буквой «t», а пространство – «x».
Обратите внимание на рис. 3. На нём изображена волна, простирающаяся в обоих направлениях на большое расстояние, на которой уместилось множество гребней и впадин. Это отличается от волны на рис. 2, у которой всего несколько гребней и впадин. Но это различие не имеет отношения к делу – на рис. 2 мне нужно был проиллюстрировать то, для чего не имела значения точная форма волны; теперь же мы сконцентрируемся на математической формуле для волн, а это гораздо проще сделать, если у волны есть большое количество гребней и впадин одинакового размера. Также этот случай окажется очень полезным для понимания того, как квантовая механика влияет поведение волн.


Рис. 3
Сначала нам нужно определиться с обозначениями и записать формулу, описывающую движение и форму волны на рис. 3, как мы делали для шара на пружине.
На графике показана величина волны Z как функция от пространства в определённый период времени t = t0 — мы записываем это, как Z(x, t0). Отслеживая волну в пространстве мы видим, что она колеблется вперёд и назад, и Z периодически увеличивается и уменьшается. В любой момент времени волна колеблется в пространстве.
Заметьте, что Z не обязательно должна быть связана с физическим расстоянием. Это может быть высота верёвки, как на рис. 2, или это может быть нечто совсем другое, к примеру, температура воздуха в определённой точке пространства и времени или ориентация магнитного атома в определённом месте магнита. Но x всё же представляет физическое расстояние, а t – время.
У снимка этой волны, Z(x, t0), есть три интересных свойства, два из которых также относятся и к шару на пружине.
1. Существует значение равновесия Z0, лежащее посередине между самым большим значением Z на гребне и самым малым значением Z во впадине. Большую часть времени мы изучаем волны, у которых Z0 = 0, поскольку часто величина Z0 не имеет значения – но не всегда.
2. У волны есть амплитуда А, величина, на которую меняется Z от равновесного значения до вершины каждого гребня или на ту же величину до дна каждой впадины.
3. У волны есть длина – расстояние λ между соседними гребнями, или, что то же самое, между соседними впадинами, или, что то же самое, удвоенное расстояние между соседними гребнем и впадиной. Она описывает колебания в пространстве так же, как период (равный 1/частоту) описывает колебание во времени шара на пружине.

Рис. 4
Что же напоминает нам форма на рис. 3? Она выглядит, как график функции синуса или косинуса – см. рис. 4, где cos(w) построен на графике по w. Cos(w) – функция осциллирующая, у которой есть очевидная позиция равновесия в нуле, её амплитуда 1, а длина волны — 2π. Как перейти от рис. 4 к формуле для волны на рис. 3? Сначала мы умножим cos(w) на А, чтобы амплитуда сравнялась с А. Затем мы добавим Z0 ко всей формуле, чтобы сдвинуть её до нужного значения равновесия (если А = 0, то колебаний нет, и всё покоится в точке Z = Z0). И, наконец, заменим w на 2πx/λ, поскольку у cos(w) гребни на w = 0 и w = 2 π, поэтому у cos(2πx/λ) гребни будут на x = 0 и x = λ. Всё вместе это даёт нам
Это практически та же формула, что описывала движение шара на пружине во времени:
Где ν – частота колебаний, а T = 1/ν – период колебаний. Видите аналогию: период относится ко времени, как длина волны к пространству.
Ещё одно замечание до того, как мы продолжим. Я мог записать также:
Поскольку cos[w] = cos[-w]. То, что мы спокойно можем подставить минус в формулу формы волны, будет важно позднее.
Формула для бесконечной волны в определённом месте

Рис. 5
Теперь зададим другой вопрос: посмотрим, как волна меняется во времени, отслеживая определённую точку на верёвке, и увидим, как она себя ведёт и двигается. Это показано на рис. 5: там я обозначил определённую точку x0, которая в момент времени t0 находится на гребне. Волна двигается вправо и следует размеру волны Z в точке x0, меняясь во времени: Z(x0, t). И вы немедленно увидите, что высота волны в определённой точке ведёт себя точно так же, как шар на пружине! Поэтому у неё будет точно такая же формула, как у шара на пружине, как функция частоты ν, или периода T = 1/ν, где T – это время между моментом, когда волна в x0 находится н а гребне, и моментом, когда она снова приближается к гребню в следующий раз.
Полная формула бесконечной волны
Теперь нам нужна формула для Z(x, t), описывающая волну, изображённую на рис. 3 и 5 (или любую похожую) в точках x в любой момент времени t. Правильный ответ:
Он включает обе формулы, для фиксированной точки во времени и для фиксированной точки в пространстве.
Отметим знак минуса перед x. Я упоминал, что в формулу для Z(x, t0) можно подставить минус по желанию. С минусом перед x и плюсом перед t формула описывает волну, движущуюся вправо, как на анимациях. Чтобы проверить это, заметьте, что когда t/T – x/λ = 0, волна будет гребнем, потому что cos[0]=1. Когда t = 0, в точке x = 0 гребень. Но если немного сдвинуть t вперёд, допустим, на T/10, то гребень будет в точке x = λ/10, правее от того места, где он был в t = 0 – поэтому гребень (и вся волна) движется вправо.

Рис. 6
Волны, являющиеся функциями x и t, могут двигаться в любом направлении, так что нам просто нужно выбрать правильную формулу для заданной волны. Вообще говоря, когда мы работаем с волнами, которые могут двигаться не только вдоль одного пространственного измерения x, но вдоль всех трёх координат x, y и z, то эти волны могут двигаться в любом направлении, и нам нужно будет выбрать правильную формулу на основании направления движения волны.
Символический метод позволяет перейти от графоаналитических расчетов с помощью векторных диаграмм к расчетам аналитическим. Это, с одной стороны, повышает точность расчетов, а с другой – значительно облегчает выполнение математических операций с синусоидальными функциями. Кроме того, символический метод позволяет без ограничений использовать для расчета цепей синусоидального тока все законы и методы, полученные для цепей постоянного тока.
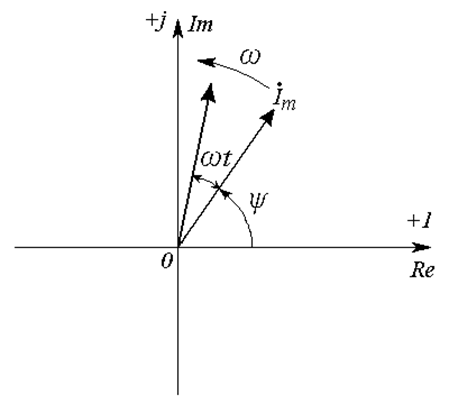
Основная идея метода состоит в перенесении известной нам векторной диаграммы на комплексную плоскость. Пусть на комплексной плоскости со скоростью 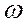
Сразу заметим, что в теоретической электротехнике принято обозначать мнимую единицу (то есть квадратный корень из минус единицы) буквой j (читается по-немецки, «йот»), чтобы не путать ее с обозначением тока.
Также все комплексные величины, изображающие токи, напряжения и мощности, принято обозначать прописной буквой с точкой сверху. Комплексные величины, изображающие параметры цепи (сопротивления, проводимости), принято обозначать прописной буквой, подчеркнутой снизу. Модуль комплексного числа будем обозначать прописной буквой, без точки и черты.
Если функция тока имеет вид:
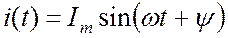
то изображающая ее комплексная функция:
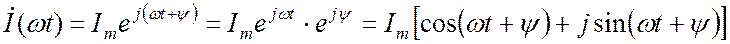
Очевидно, что исходная синусоидальная функция (18.1) совпадает с мнимой частью комплексной функции (18.2).
Как правило, в цепях действуют источники одной и той же частоты, поэтому нет необходимости вращать векторы. А это означает, что сомножитель 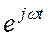
Итак, все реальные синусоидальные функции заменяются комплексными числами. Расчеты проводятся в комплексной форме. Окончательный результат переводится в синусоидальную форму.
Заметим, что чаще всего при расчетах используются не амплитудные, а действующие значения токов и напряжений. Следует придерживаться этого правила.
Рассмотрим некоторые свойства комплексных чисел.
Как известно, любое комплексное число можно изобразить точкой на комплексной плоскости. В зависимости от способа описания координат этой точки можно выделить две формы комплексного числа – алгебраическую и показательную.
Алгебраическая форма комплексного числа соответствует декартовой системе координат на комплексной плоскости (Рис. 18.2):
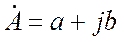
где a – действительная часть числа (координата по оси Re);
b – мнимая часть числа (координата по оси Im).
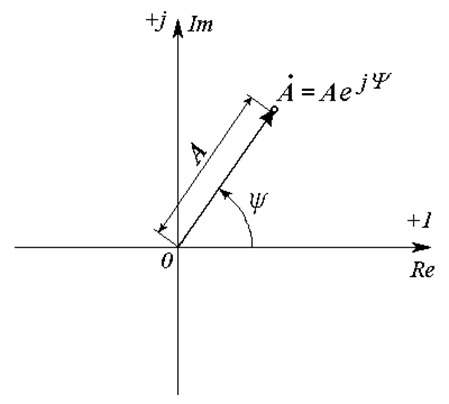
Показательная форма комплексного числа соответствует полярной системе координат на комплексной плоскости (Рис. 18.3):
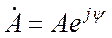
где A – модуль комплексного числа (длина радиус-вектора, соединяющего начало координат
с точкой 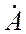
Ψ – угол комплексного числа (откладывается от положительной полуоси действительных
чисел; против часовой стрелки – со знаком плюс, по часовой стрелке – со знаком минус).
Алгебраическая и показательная формы связаны друг с другом через тригонометрическую форму комплексного числа:
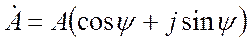
Из (18.5) выводятся формулы для перевода комплексного числа из одной формы в другую.
При переводе комплексного числа из показательной формы в алгебраическую используют соотношения:
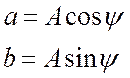
При переводе комплексного числа из алгебраической формы в показательную используют соотношения:
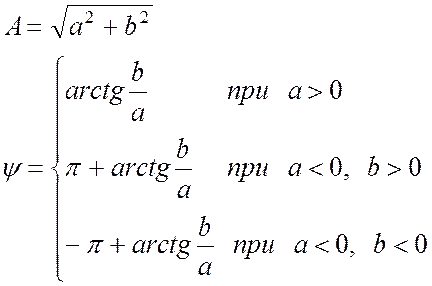
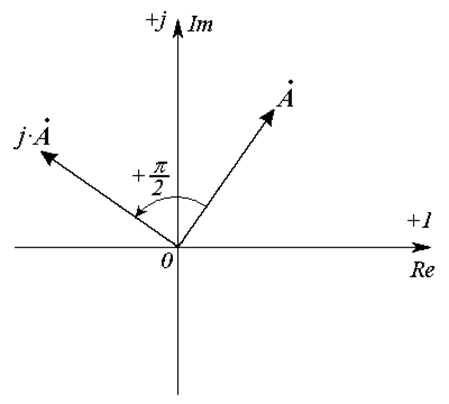
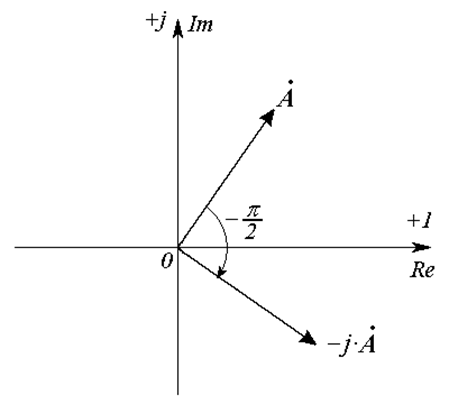
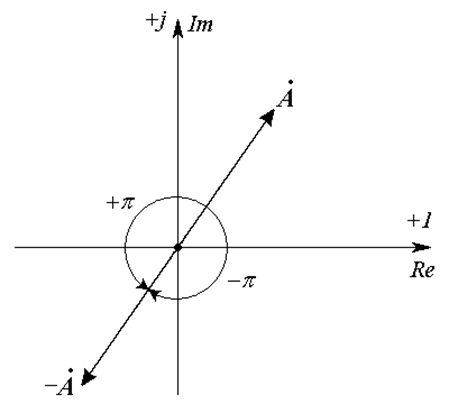
Умножение комплексного числа на 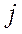
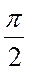
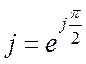
Умножение комплексного числа на 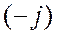
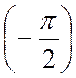
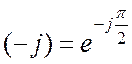
Умножение комплексного числа на 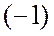
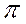
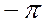
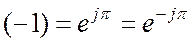
Дифференцирование синусоидальной функции соответствует умножению ее комплексного изображения на 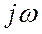
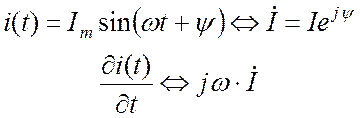
Интегрирование синусоидальной функции соответствует делению ее комплексного изображения на 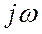
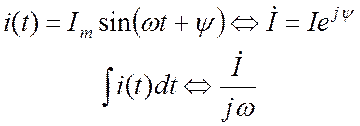
Если в знаменателе дроби стоит чисто мнимое число (то есть число, действительная часть которого равна нулю), мнимая единица переносится в числитель путем умножения числителя и знаменателя на 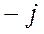
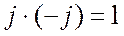
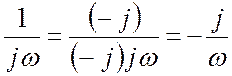
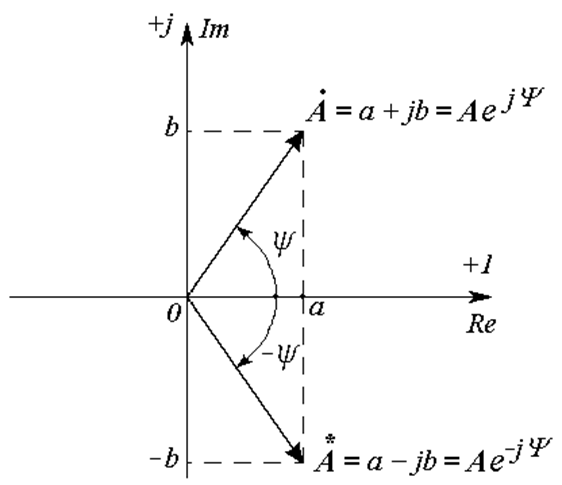
Если в знаменателе дроби стоит число с неравной нулю действительной частью, числитель и знаменатель дроби умножают на комплексно-сопряженное число. Комплексно-сопряженным числом называют число, симметричное данному относительно действительной оси (Рис. 18.7). Обозначается звездочкой сверху.
Здесь используется известное равенство:
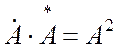
Произведение двух комплексно-сопряженных чисел равно квадрату их модуля.
Для переноса мнимой единицы в числитель умножим числитель и знаменатель на комплексно-сопряженное число:
Чтобы распечатать файл, скачайте его (в формате Word).