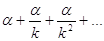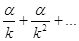Апория зенона стадий показывает что
Апория зенона стадий показывает что
Проблема – как, в конечном счете, устроены геометрические объекты, из чего они «состоят» – была важной проблемой для греческой философии. Эта проблема привлекла внимание и Зенона – представителя Элейской философской школы. Элейская школа выступала с парадоксальным учением, что существует только единое и неподвижное и неизменное бытие, повсюду одинаковое: хотя людям кажется, что бытие множественно и подвержено переменам, это мнение ведет к противоречиям и поэтому должно быть отброшено.
Наиболее известными и важными для математики стали сформулированные Зеноном четыре апории (т. е. парадокса), направленных против существования движения. По-видимому, первые две апории Зенона подразумевали, что пространство и время делимы до бесконечности, а другие две основывались на противоположном представлении, будто пространственная протяженность и временная длительность состоят из неделимых моментов. Зенон пытался показать, что каждое из двух противоположных воззрений в результате ведет к противоречию, а значит, должна быть отвергнута сама идея движения, которое представляет собой лишь иллюзию.
Движущееся тело никогда не достигнет конца пути, потому что оно сначала должно дойти до середины пути, потом до середины оставшегося пути, потом опять до середины остатка и т. д. – таким образом, прежде чем дойти до конца пути, тело должно пройти бесконечное множество середин, а это потребует бесконечного времени.
Быстроногий Ахиллес никогда не сможет догнать медлительной черепахи, если в начале движения она находится на некотором расстоянии впереди Ахиллеса: пока Ахиллес достигнет черты, с которой стартовала черепаха, она сама проползет на некоторое расстояние, пусть и меньшее; пока Ахиллес пробежит это расстояние, черепаха продвинется еще дальше, и т. д.
В каждый момент времени летящая стрела занимает равное самой себе пространство. Следовательно, она в течение некоторого времени покоится. Таким образом, она и вовсе не движется.
По стадиону мимо группы равных тел А1, А2, А3, А4 движутся в противоположные стороны с одинаковыми скоростями еще две такие же группы – В1, В2, В3, В4 и Г1, Г2, Г3, Г4. Раз они движутся с равной скоростью, то в равное время пройдут равное расстояние. Если за некоторое время первое из тел В пройдет мимо всех Г, то за это же время первое из тел Г пройдет мимо половины тел А, а значит, оно пройдет лишь половину того расстояния, который прошло тело В, а значит – так как В и Г движутся с равными скоростями – оно прошло и половину того времени, за которое тело В прошло все тела Г. С другой стороны, за одно и то же время первое из тел Г пройдет мимо всех В, а первое из В пройдет лишь половину тел А, и значит, в два раза меньшее расстояние, затратив в два раза меньшее время, чем тело Г, прошедшее все тела В. Получается, что одно и то же время и вдвое длиннее, и вдвое короче, чем оно же само.
Хотя большинство философов не могли принять странные выводы Зенона о несуществовании движения, поставленные Зеноном проблемы заставили более пристально вглядываться в понятия, связанные с пространством и временем. Так, Аристотель полагал, что пространство и время не состоят из некоторого числа отдельных точек и моментов, но представляют собой особый тип сущего – нечто непрерывное, или, как еще говорят, континуум (лат. continuum – непрерывное). Пространственные и временные отрезки в действительности делимы до бесконечности, но делимы лишь потенциально, в том смысле, что любой отрезок можно разделить некоторой точкой, то, что осталось, тоже можно разделить, и т. д., но невозможно в какой-то момент реализовать бесконечное количество делений, – точно так же, как всякий раз возможно продлить имеющийся отрезок на некоторую величину, но нельзя считать бесконечное число таких продлений уже реализованным. Невозможно иметь в наличии бесконечную прямую, и нельзя сказать, что на отрезке уже находится бесконечное количество точек. Вот если бы в первой апории идущий человек каждый раз, проходя середину очередного отрезка, останавливался бы, отмечая эту середину, – тогда его движение не было бы непрерывным и он никогда бы не смог пройти весь отрезок. Решение Аристотеля было принято многими математиками: с подобными соображениями связано и разграничение Евклида между прерывными числами, с одной стороны, и непрерывными величинами, с другой стороны (см. урок 6). Тем не менее, на этом рассмотрение бесконечности в математике не закончилось: так, уже в XIX в. Г. Кантор развил теорию множеств, позволявшую рассматривать отрезок как бесконечное множество точек. Такое рассмотрение позволило открыть новые ценные результаты, а также поставить новые интересные проблемы, связанные, в частности, с некоторыми противоречиями, содержащимися в теории бесконечных множеств.
Кроме того, апории Зенона связаны и с рядом других вопросов, касающихся математики (суммирование бесконечного числа слагаемых, относительность движения, соотношение математической теории и физической реальности и т. д.).
Интересно, а Вы что думаете об этих апориях?
Апории Зенона
Проблема бесконечности и развитие античной диалектики
Зенон выдвинул ряд парадоксальных положений, которые получили название апорий («апория» в переводе с греческого означает «затруднение», «безвыходное положение»). С их помощью он хотел доказать, что бытие едино и неподвижно, а множественность и движение не могут быть мыслимы без противоречия, и потому они не суть бытие.
Первая из апорий — «Дихотомия» (что в переводе с греческого означает «деление пополам») доказывает невозможность мыслить движение. Зенон рассуждает так: чтобы пройти какое бы то ни было, пусть самое малое расстояние, надо сначала пройти его половину и т. д. без конца, поскольку любой отрезок линии можно делить до бесконечности. И в самом деле, если непрерывная величина (в данном случае — отрезок линии) мыслится как актуально данное бесконечное множество точек, то «пройти», «просчитать» все эти точки ни в какой конечный отрезок времени невозможно.
Группа ВКонтакте — Философия одной Души
На том же допущении актуальной бесконечности элементов непрерывной величины основана и другая апория Зенона — «Ахиллес и черепаха». Зенон доказывает, что быстроногий Ахиллес никогда не сможет догнать черепаху, потому что, когда он преодолеет разделяющее их расстояние, черепаха проползет еще немного, и так всякий раз до бесконечности.
В третьей апории — «Стрела» — Зенон доказывает, что летящая стрела на самом деле покоится и, значит, движения опятьтаки на самом деле нет. Он разлагает непрерывность времени на сумму дискретных (неделимых) моментов, отдельных «теперь», а непрерывность пространства — на сумму отдельных неделимых отрезков. В каждый момент времени стрела, согласно Зенону, занимает определенное место, равное ее величине. Но это означает, что она в каждый момент неподвижно покоится, ибо движение, будучи непрерывным, предполагает, что предмет занимает место большее, чем он сам. Значит, движение можно мыслить только как сумму состояний покоя, и, стало быть, никакого движения нет, что и требовалось доказать. Таков результат, вытекающий из допущения, что протяженность состоит из суммы неделимых «мест», а время — из суммы неделимых мгновений. Движение ведь предполагает бесконечную делимость как пространства, так и времени.
Таким образом, как из допущения бесконечной делимости (которая, видимо, по Зенону, предполагает актуально бесконечное множество «точек» в любом отрезке), так и из допущения неделимости отдельных моментов времени Зенон делает один и тот же вывод: ни множество, ни движение не могут быть мыслимы без противоречия, а поскольку для элеатов бытие и мышление — одно и то же, тождественны, то движение и множественность не существует поистине, а только во мнении.
Парадоксы Зенона нередко рассматривались как софизмы, сбивающие людей с толку и ведущие к скептицизму. Характерно одно из опровержений Зенона философом Антисфеном. Выслушав аргументы Зенона, Антисфен встал и начал ходить, полагая, что доказательство действием сильнее всякого словесного возражения.
Несмотря на то что с точки зрения здравого смысла апории Зенона могут восприниматься как софизмы, на самом деле это — не просто игра ума: впервые в истории человеческого мышления здесь обсуждаются проблемы непрерывности и бесконечности. Зенон сформулировал вопрос о природе континуума, который является одним из «вечных вопросов» для человеческого ума.
Апории Зенона сыграли важную роль в развитии античной диалектики, как и античной науки, особенно логики и математики. Диалектика единого и многого, конечного и бесконечного составляет одну из наиболее важных заслуг Платона, в чьих диалогах мы находим классические образцы древнегреческой диалектики. Интересно, что понятие актуально бесконечного, введенное Зеноном для того, чтобы с его помощью доказать от противного основные положения онтологии Парменида, было исключено из употребления как в греческой философии (его не признавали ни Платон, ни Аристотель), так и в греческой математике. И та, и другая оперировала понятием потенциальной бесконечности, то есть бесконечной делимости величин, но не признавала их составленности из бесконечно большого числа актуально данных элементов.
Итак, в понятии бытия, как его осмыслили элеаты, содержится три момента: 1) бытие есть, а небытия нет; 2) бытие едино, неделимо; 3) бытие познаваемо, а небытие непознаваемо: его нет для разума, а значит, оно не существует.
Понятие единого играло важную роль также у пифагорейцев. Последние объясняли сущность всех вещей с помощью чисел и их соотношений, тем самым способствуя становлению и развитию древнегреческой математики. Началом числа у пифагорейцев выступало единое, или единица («монада»). Определение единицы, как его дает Евклид в VII книге «Начал», восходит к пифагорейскому: «Единица есть то, через что каждое из существующих считается единым». Единое, согласно пифагорейскому учению, по своему статусу выше множественности; оно служит началом определенности, дает всему предел, как бы стягивая, собирает множественное. А там, где налицо определенность, только и возможно познание: неопределенное — непознаваемо.
Апория «Стадий» («Стадион»)
2.2.3. Апория «Стадий» («Стадион»).
2.2.3.1. Формулировка апории.
Пусть по стадиону движутся по параллельным прямым равные массы с равной скоростью, но в противоположных направлениях. Пусть ряд А1, А2, А3, А4 означает неподвижные массы. Ряд В1, В2, В3, В4 означает массы, движущиеся вправо, а ряд Г1, Г2, Г3, Г4 означает массы, движущиеся влево.
2.2.3.2. Логическая ошибка в основе апории «Стадий»
2.2.4. «Ахиллес и черепаха».
Быстроногий Ахиллес никогда не догонит черепаху, если в начале движения черепаха находилась на некотором расстоянии впереди него. Действительно, пусть начальное расстояние есть α и пусть Ахиллес бежит в k раз быстрее черепахи. Когда Ахиллес пройдет расстояние α, черепаха отползет на α/k, когда Ахиллес пройдет это расстояние, черепаха отползет на α/k2, и так далее, то есть всякий раз между состязающимися будет оставаться отличное от нуля расстояние.
2.2.4.2. Противоречивость апории.
В этой апории, помимо того же затруднения отсчитанной бесконечности, имеется и еще одно. Предположим, что в некоторый момент времени tω Ахиллес догонит черепаху. Запишем путь Ахиллеса
SA=
SA=
Каждому отрезку пути 
, пройденному Ахиллесом, соответствует отрезок пути 
черепахи. Поэтому к моменту встречи Ахиллес должен пройти «столько же» отрезков пути, сколько и черепаха. С другой стороны, каждому отрезку пути , пройденному черепахой, можно сопоставить равный ему по величине отрезок пути Ахиллеса. Но, кроме того, Ахиллес должен пробежать еще один отрезок длины α, то есть он должен пройти на единицу больше отрезков, чем черепаха. Если количество отрезков, пройденное последней, есть α, то получаем
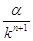
Зенон, как известно, не отрицавший реальности движения, не смог лишь логически последовательно осмыслить последнее, допуская трудно обнаружимое нарушение основных логических принципов. Констатируя этот факт, В.И. Ленин высказал свое замечание: «Вопрос не в том, есть ли движение, а как его выразить в логике понятий», чтобы избежать при этом формально логической непоследовательности. Задача эта вполне разрешима уже с помощью средств, которыми располагает современная символическая логика и которые позволяют логически непротиворечиво отобразить диалектическую противоречивость объективно реального процесса движения.
2.2.5.1. Формулировка апории.
Если время и пространство состоят из неделимых частиц, то летящая стрела неподвижна, так как в каждый неделимый момент времени она занимает равное себе положение, то есть покоится, а отрезок времени и есть сумма таких неделимых моментов.
Эта апория направлена против представления о непрерывной величине как о сумме бесконечного числа неделимых частиц.
2.2.5.2. Основная логическая ошибка в апории «Стрела»
однотипна ошибкам в уже рассмотренных нами апориях: налицо непосредственное нарушение прежде всего логического принципа тождества, а отсюда следует нарушение прочих принципов. Оно выражается в неявном смешении понятий покоя и механического движения, осуществляемом посредством употребления понятия «находиться», «пребывать» в качестве ближайшего родового понятия по отношению к понятиям покоя и движения. Однако покой тела в онтологическом плане не является движением (в противном случае движение действительно должно было бы считать суммой состояний покоя), а выступает как абсолютное, недиалистическое отрицание механического движения в момент пересечения последнего. Поэтому и в логическом плане нельзя считать «покой» и «движение» видовыми в отношении понятий «находиться», «пребывать».
3. Влияние Зенона на философию Древней Греции как подтверждение реконструированного учения.
В своей работе я коснулся только некоторых математико-философских вопросов, связанных с парадоксами Зенона. Но сам Зенон придал своим апориям ярко выраженный физический смысл: он направил их против возможности движения. Основной вопрос состоит в соотношении математической модели и реального физического пространства.
В апориях Зенона предполагается, что пространство в малом устроено так же, как и в большом, факты из области движения величин определенного порядка переносятся на все величины. Между тем согласно современным физическим взглядам физические величины вовсе не являются делимыми до бесконечности. Современная физика открывает все новые и новые замечательные факты о строении микромира. Д. Гильберт и П. Бернайс в своей книге «Основания математики» (1934) писали, что решение парадокса «дихотомия» состоит «в указании на то обстоятельство, что мы вовсе не обязательно должны верить в то, что математическое пространственно-временное представление движения имеет физическое значение для произвольно малых интервалов пространства и времени; скорее, мы имеем все основания предполагать, что эта математическая модель экстраполирует факты из некоторой области опыта, а именно из области движений в пределах того порядка величин, который пока доступен нашему наблюдению, экстраполирует просто в смысле образования идей, подобно тому, как механика сплошной среды совершает экстраполяцию, предполагающую непрерывное заполнение пространства материей… Ситуация оказывается сходной во всех случаях, когда имеется вера в возможность непосредственного узрения(актуальной) бесконечности как данной посредством опыта или восприятия… Более подробное исследование показывает затем, что бесконечность вовсе не была нам дана, а была только интерполирована или экстраполирована посредством некоторого интеллектуального процесса».
Мы видим, что апории Зенона затронули действительно глубокие и сложные вопросы. Как же ответила на них античная наука? В частности, как она разрешила вопрос о том, допустимо ли пользоваться в математике актуально бесконечно большими и актуально бесконечно малыми величинами? Мы можем судить о тех точках зрения, которые имели место в античной математике, и о тех дискуссиях, которые там велись, по косвенным данным, главным образом по сообщениям Аристотеля и других философов этого времени.
Четырьмя парадоксами Зенон очень хорошо достигает того, чего хотел. Он логически строго показывает, что в пифагорейских представлениях о движении, пространстве и времени что-то неверно. Эти демонстрационные примеры Зенона не убедили более поздних мыслителей принять выводы Парменида, однако заставили этих мыслителей проникнуться уважением к формальной логике и увидеть новые возможности ее применения. Еще они, естественно, заставили их попытаться сформулировать пифагорейские понятия по-новому, таким образом, чтобы исключить показанные Зеноном противоречия. Эти попытки имели много форм: у Анаксагора – отказ от представления об отдельных точках и замена их непрерывной последовательностью, у Аристотеля – полное отделение арифметики от геометрии, а в атомистической теории – лежащее в ее основе четкое разграничение физической и математической «делимости».
Грюнбаум А. Философские проблемы пространства и времени. М., 1969.
История математики с древнейших времен до начала XIX столетия. Том 1, 1970.
Комарова В. Я. Учение Зенона Элейского. //Вестник Ленинградского университета, 1981.
Манеев А. К. Философский анализ зеноновских апорий. Минск, 1972.
Отношение движения тела и покоя в апориях Зенона Элейского
Древнегреческого философа Зенона Элейского (около 490-430 до н. э.) Аристотель считал основателем диалектики. Зенон Элейский принял за основу своих апорий отношение друг к другу состояния движения тела к его состоянию покоя. Он установил, что, что движение есть покой, покой не есть движение. Движение тела есть его покой постольку, поскольку они едины и неразличимы. Покой тела не есть его движение постольку, поскольку они прямо противоположны. Состояние движения тела и его состояние покоя неразделимы, взаимно друг друга определяют, предполагают и исключают. Их отношение друг к другу представляет собой единство противоположностей, каждая из которых переходит в свою противоположность.
Единство состояния движения и состояния покоя тела выражено Зеноном Элейским в его парадоксах (апориях) в такой иносказательной форме, в которой они озадачивают, вызывают недоумение и напрашиваются на опровержение. Он целенаправленно маскирует и затемняет их опосредствованное отношение друг к другу, чтобы выдать его за непосредственное отношение. С этой целью единство движения и покоя Зеноном изымается из поля зрения, переход их друг в друга утаивается, а их относительная противоположность ярко высвечивается и выдаётся за абсолютную противоположность. По Зенону, движение тела преходяще, конечно, недостоверно и немыслимо, а покой этого же тела вечен, бесконечен, достоверен и мыслим.
Зенон Элейский непрерывному мыслимому единому бытию противопоставлял дискретное чувственно воспринимаемое множество многообразных вещей, существующих в состоянии движения и изменения. Это им делалось и выражалось не в явной форме математических предложений, а в камуфляжной форме загадок-парадоксов. Сам о себе он мог бы сказать: я установил для философов, физиков и математиков множество исключительно красивых загадок.
За две с лишним тысячи лет своего существования загадки-апории Зенона Элейского не утратили своего значения. Они и в наше время доставляют много труда каждому, кто проявляет к ним глубокий интерес.
Формулировки дихотомии, Ахиллеса и стрелы мной взяты из книги «Творцы математики» Э. Т. Белла /Э.Т.Белл «Творцы математики». М.,1979, стр.33 /.
«1. ДИХОТОМИЯ (разделение на два). Движение невозможно, так как, что бы ни двигалось, оно ПРЕЖДЕ, чем достичь конца пути, должно достигнуть его середины, а ещё РАНЬШЕ этого должно достигнуть одной четверти пути и т. д. — без КОНЦА. Следовательно, движение не может никогда даже начаться»
«2. АХИЛЛЕС. Бегущий Ахиллес никогда не сможет догнать ползущую перед ним черепаху, так как прежде всего он должен добежать до того места, откуда отправилась черепаха, но, пока Ахиллес сделает это, черепаха уже уползёт с того места и снова окажется впереди. Повторяя этот довод и дальше, мы заключаем, что черепаха всегда будет впереди».
Утверждение о том, что бегущий Ахиллес никогда не сможет догнать ползущую перед ним черепаху, является заключением правильного математического предложения. Существование правильного условия, из которого следует данное заключение, можно будет найти. Условием заключения может быть определённая форма существования Ахиллеса в собственном времени и пространстве.
По предложению 1, если Ахиллес находится в состоянии движения, то он существует определённое время в неопределённом пространстве. Неопределённое пространство не имеет определённой длины, определённого направления, начала и конца. Бег Ахиллеса в течение определённого промежутка времени в неопределённом пространстве, которое не имеет определённого направления и определённоё длины на не приведёт его к определённому месту, откуда отправилось черепаха.
Если Ахиллес находится на определённом расстоянии от места, откуда отправились черепаха, то он существует на определённой длине определённого пространства неопределённое время.
По предложению 4, если Ахиллес существует на определённоё длине определённого пространства, имеющей начало и конец, неопределённое время, то он находится в состоянии покоя. В состоянии покоя он может находиться в положении стоя, сидя, лёжа, или в каком-нибудь другом положении, но в любом случае он не сможет даже сдвинуться со своего места и тем более не сможет добежать до того места, откуда отправилась черепаха.
Итак, открылись два прямо противоположных условия, из которых следует одно и то же заключение: бегущий Ахиллес никогда не сможет догнать ползущую перед ним черепаху.
По первому условию, Ахиллес существует в собственном определённом времени в неопределённом пространстве в состоянии движения. По второму условию, он существует неопределённое время в определённом пространстве в состоянии покоя. Оба условия соответствуют отношению времени и пространства Ахиллеса как соотношению неопределённостей, но не соответствуют их отношению друг к другу, как единству противоположностей, каждая одна из которых переходит в другую.
В данной апории тайно и умышленно Зеноном Элейским изъято время обращения состояния движения Ахиллеса в состояние покоя. Кроме этого, изъят процесс их обращения. Действительное отношение друг к другу этих состояний Ахиллеса представлено в апории в искусственной абстрактной форме математического предложения, в котором заключение следует из условия непосредственно вне времени, минуя процесс обращения. В условии математического предложения состояние движения и покоя Ахиллеса абсолютно неразличимы, а в его заключении состояние покоя абсолютно противоположно состоянию движения. Недостоверность абстрактного математического предложения, представляющего собой основу апории, не может быть никем ни доказана, ни опровергнута. Она может быть только разгадана.
«3. СТРЕЛА. Движущаяся стрела в каждый момент времени либо находится в покое, либо нет, т.е. движется. Если момент времени неделим, то стрела в этот момент не может двигаться, ибо если бы она двигалась, то момент немедленно можно было бы разделить. Но если стрела не может двигаться в каждый момент, то она не может двигаться вообще, ибо время складывается из моментов. Следовательно, она всегда пребывает в покое».
Первая фраза апории представляет собой математическое предложение, которое утверждает, что состояние покоя и состояние равномерного прямолинейного движения стрелы неразличимы: она либо находится в покое, либо движется.
На основании того, что состояния стрелы неразличимы, можно прийти к заключению о том, что движущаяся стрела существует в собственном времени и в собственном пространстве, которые различить невозможно: промежуток времени есть длина пространства, длина пространства есть промежуток времени.
Вся последующая часть апории «Стрела» представляет собой математическое предложение, которое утверждает абсолютную противоположность состояния покоя стрелы и её состояния равномерного прямолинейного движения: покой не есть движение, длина пространства не есть промежуток времени.
Сколько собственного времени существует стрела в состоянии движения, столько же времени она существует, осуществляя переход из состояния движения в состояние покоя, и столько же времени она существует в состоянии покоя. Средняя форма существования стрелы существования стрелы и время существования стрелы в этой форме Зеноном в глубокой тайне приравнивается нулю. Дело представляется таким образом, что будто бы стрела в каждый момент времени момент времени либо находится в покое, либо движется, а в следующий неделимый момент времени не может двигаться и не может двигаться вообще, «ибо время складывается из моментов».
Да, определённое делимое время складывается из делимых моментов. Но Зенон Элейский умышленно лукавит: ни какое время тела — как определённое, так и неопределённое — не складывается из делимых и неделимых моментов времени.
Сложение Зеноном делимых моментов времени и неделимого моментов времени стрелы в одну общую сумму является ошибочным и недопустимым. Но на действие сложения надевается маска, чтобы нельзя было догадаться о том, что слагаемые не складываются. Результат сложения принимается за «достоверное» условие математического предложения, из которого выводится «правильное» заключение: если стрела не может двигаться в каждый момент времени, то она не может двигаться вообще. Следовательно, она всегда пребывает в покое.
«4. СТАДИЙ. Если два тела движутся друг к другу с одинаковой скоростью, то они встретятся на половине пути через определённый промежуток времени. Если же одно тело будет двигаться с этой же скоростью, а другое покоиться, то они встретятся через промежуток времени вдвое больший. Следовательно, движение, то есть приближение одного тела к другому, будет разным в зависимости от точки зрения на него, то есть само по себе оно вовсе не есть движение».
Первая фраза апории «Стадий» представляет собой кромешную темноту, в которой ничего невозможно видеть.
Только ведь противоречие состояния движения тела требует своего разрешения, требует реализации процесса обращения возможности в действительность. Нереализованная возможность остаётся лишь возможностью и не становится действительностью. Поэтому в апории состояния движения тела остаётся только возможностью, а состояние покоя тела не образуется из состояния покоя, а берётся как данная единственная реальность, которая утверждает невозможность состояния движения. На этой основе и принимается заключение: движение, т. е. приближение одного тела к другому, будет разным в зависимости от точки зрения на него, т. е. само по себе оно вовсе не есть движение.
Можно предположить, и не без основания, что Зенон исключал самый процесс обращения состояния движения в свою противоположность не потому, что не знал, что он существует. Он знал его, но исключал с определённой целью: создать апорию-загадку, заключающую в себе противоречие, разрешение которого доставит философам много труда.
Имеются свидетельства о том, что Зенон Элейский не происходил из знатного рода. По этой причине, надо полагать, испытывал на себе пренебрежительное отношение со стороны лиц знатного происхождения, которые его третировали ещё и как самоучку. Он же обладал непревзойдённым уровнем диалектического мышления и способностью создавать апории, которые его кичливые недоброжелатели не могли ни принять, ни опровергнуть.
Отношение движения тела и покоя в апориях Зенона Элейского: 3 комментария
Завершая начинания Зенона на примере парадоксов разносторонне показавшего абсурдность применения МЕТОДА ЗАВУАЛИРОВАННОГО ОТРИЦАНИЯ (МЗО) к сфере чувственно постигаемого, основанного на отождествлении с математической точкой составляющих этой сферы, Леметр санкционировал законность применение МЗО к сфере умопостигаемого! Баланс в постижении обоих сфер нарушенный констатациями элейца «восстановился» благодаря предположениям бельгийского священника-физика… Не разобравшись с сутью апорий трудно противостоять научной интерпретации космологического вопроса!
Для того, чтобы представить ИЗНАЧАЛЬНОЕ БЕСПРЕДЕЛЬНОЕ ПРОСТРАНСТВО (изн. БП-о) разновидно ЭЛЕМЕНТНО (Эл-тно) завершённым НЕОБХОДИМО И ДОСТАТОЧНО (НИД-о) постулировать присутствие в нём двух Эл-тов с ПРОСТО и СЛОЖНО/ замкнуто системно проявляемыми СУЩНОСТЯМИ (Сщ-ями), а для представления изн. БП-а разнородно Эл-тно завершённым НИД-о постулировать присутствие в нём ещё одного Эл-та – Всевышнего и Всемогущего Бога – имеющего незамкнуто системно проявляемую Сщ-ь. Нетрудно предположить то, что уже при НИД-ном минимальном прирашении НЕМАТЕРИАЛЬНОЙ СОСТАВЛЯЮЩЕЙ (неМ-ой Сс-ей) Сщ-и Бога – Духа Божьего – НИД-о минимально нисходяще направленно постоянно развёртываемой от М-ой Сс-ей Сщ-и Бога происходит преодоление противопроявляемости Его Сщ-и вследствие распада Сщ-ей ПРОСТО и СЛОЖНО ввиду блокирования исхождения восходяще направленно постоянно развёртываемых неМ-ых Сс-их их Сщ-ей. На основе М-ых Сс-их от бывших ПРОСТО и СЛОЖНО Богом развёртываются Сщ-но противопроявляемые (Адаму изначально противостоят ангелы в числе которых ещё не проявившийся сатана) Эл-ты производного БП-а. /остальное изложено в завершающем варианте «Кратчайшей философии бытия»/
Зенон раскрыл картину дискредитации как фиксируемого в ОТНОШЕНИЯХ (Отн-ях) с Сс-ими сферы ЧУВСТВЕННО ПОСТИГАЕМОГО объективного /Отн-ях №2/, так и самих Отн-й №2 с их представляющим пространственно-временным континуумом, что, однако, не могло удержать тех, кто легко оперирует зафиксированным в Отн-ях №2 от попыток:
1. дискредитации Отн-й с Сс-ими сферы УМОПОСТИГАЕМОГО объективного /Отн-й №1/ и их представляющего БП-а понятиями «изотропная однородность», «сингулярность» не отвечающим требованиям принципа качественно и количественно Эл-тной НИД-ости для представления изн.БП-а – так полагается базис для космологии.
2. экстраполяции фиксируемого в Отн-ях №2 на Отн-я №1 – так посредством понятий ложных для Отн-й №1, но верных для Отн-й №2 развёртывается надстройка космологии. Неудивительно, что доказательной базой для такой «науки» должен был стать канувший в бесперспективность БАК (большой андроидный коллайдер).