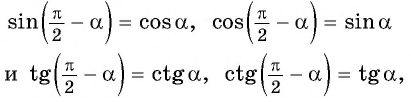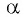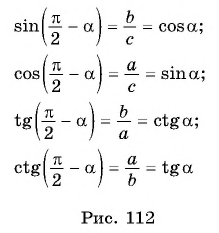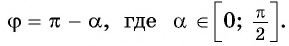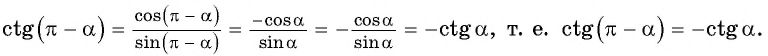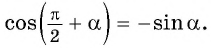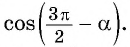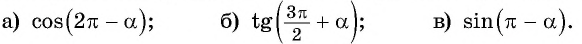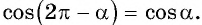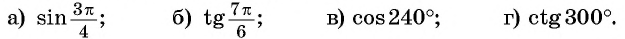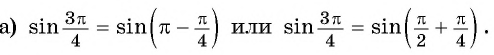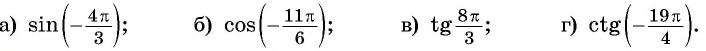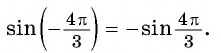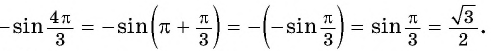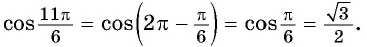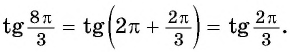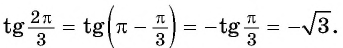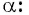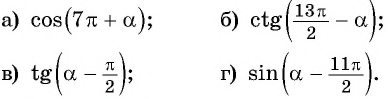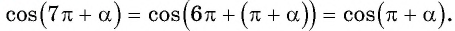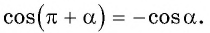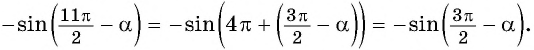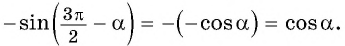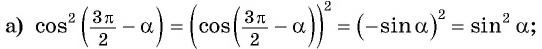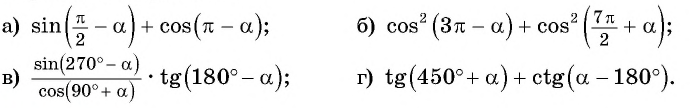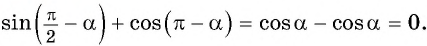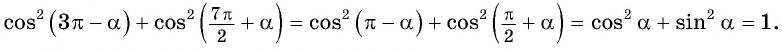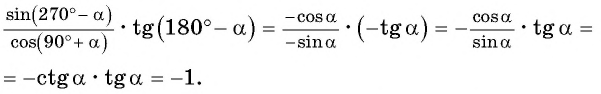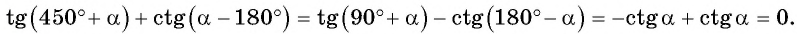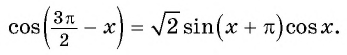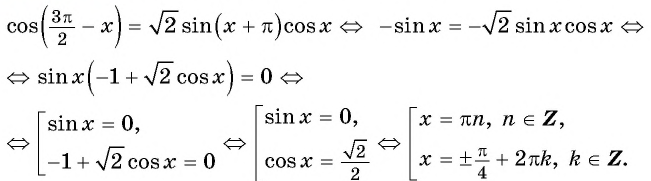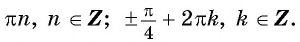Как использовать формулу приведения тригонометрия

Формулы приведения. Как быстро получить любую формулу приведения

Формулы приведения разработаны для углов, представленных в одном из следующих видов: \(\frac<\pi><2>+a\), \(\frac<\pi><2>-a\), \(π+a\), \(π-a\), \(\frac<3\pi><2>+a\), \(\frac<3\pi><2>-a\), \(2π+a\) и \(2π-a\). Аналогично их можно использовать для углов представленных в градусах: \(90^°+a\), \(90^°-a\), \(180^°+a\), \(180^°-a\), \(270^°+a\), \(270^°-a\), \(180^°+a\), \(180^°-a\). К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.

Как быстро получить любую формулу приведения

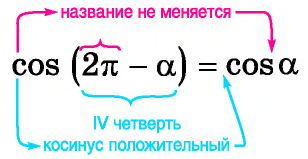
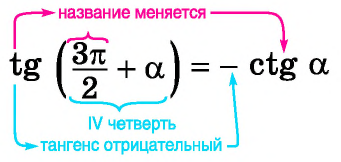
Для начала обратите внимание, что все формулы имеют похожий вид:

Едем дальше. Так как исходная функция и ее аргумент нам обычно даны, то весь вывод нужной формулы сводится к двум вопросам:
— как определить знак перед конечной функцией (плюс или минус)?
— как определить меняется ли функция на кофункцию или нет?

Как определить знак перед конечной функцией (плюс или минус)?

Какой знак был у исходной функции в исходной четверти, такой знак и нужно ставить перед конечной функцией.

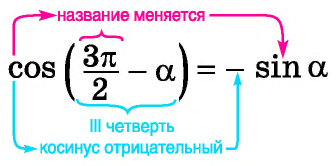
Для того, чтобы ответить на этот вопрос, представим, что \(a\) – угол от \(0\) до \(\frac<\pi><2>\), т.е. лежит в пределах \(0°…90^°\) (хотя это может быть не так, но для определения знака данная условность необходима). В какой четверти тригонометрической окружности при таком условии будет находиться точка, обозначающая угол \(\frac<3\pi><2>-a\)?
Чтобы ответить на вопрос, надо от точки, обозначающей \(\frac<3\pi><2>\), повернуть в отрицательную сторону на угол \(a\).

В какой четверти мы окажемся? В третьей. А какой же знак имеет косинус в третьей четверти? Минус. Поэтому перед итоговой функцией будет стоят минус: \(cos(\frac<3\pi><2>-a)=-. \)

Источник

Формулы приведения тригонометрических функций

Формулы приведения — это соотношения, которые позволяют перейти от тригонометрических функций синус, косинус, тангенс и котангенс с углами `\frac <\pi>2 \pm \alpha`, `\pi \pm \alpha`, `\frac <3\pi>2 \pm \alpha`, `2\pi \pm \alpha` к этим же функциям угла `\alpha`, который находится в первой четверти единичной окружности. Таким образом, формулы приведения «приводят» нас к работе с углами в пределе от 0 до 90 градусов, что очень удобно.

Формулы приведения: список и таблицы

Всех вместе формул приведения есть 32 штуки. Они несомненно пригодятся на ЕГЭ, экзаменах, зачетах. Но сразу предупредим, что заучивать наизусть их нет необходимости! Нужно потратить немного времени и понять алгоритм их применения, тогда для вас не составит труда в нужный момент вывести необходимое равенство.

Сначала запишем все формулы приведения:

Для угла (`\frac <\pi>2 \pm \alpha`) или (`90^\circ \pm \alpha`):

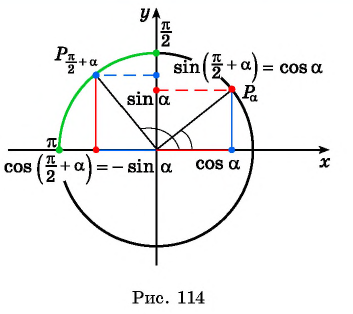
`sin(\frac <\pi>2 — \alpha)=cos \ \alpha;` ` sin(\frac <\pi>2 + \alpha)=cos \ \alpha`
`cos(\frac <\pi>2 — \alpha)=sin \ \alpha;` ` cos(\frac <\pi>2 + \alpha)=-sin \ \alpha`
`tg(\frac <\pi>2 — \alpha)=ctg \ \alpha;` ` tg(\frac <\pi>2 + \alpha)=-ctg \ \alpha`
`ctg(\frac <\pi>2 — \alpha)=tg \ \alpha;` ` ctg(\frac <\pi>2 + \alpha)=-tg \ \alpha`

Для угла (`\pi \pm \alpha`) или (`180^\circ \pm \alpha`):

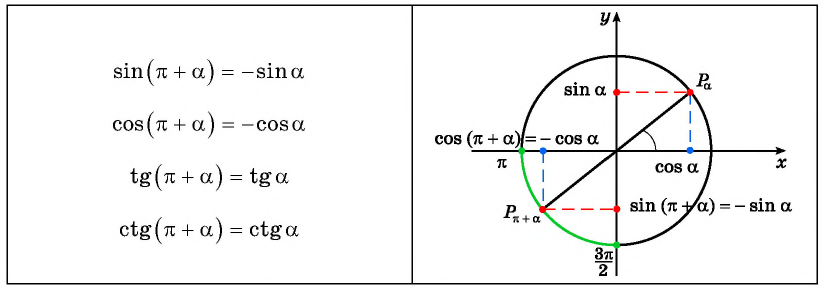
`sin(\pi — \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi — \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi — \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi — \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`

Для угла (`\frac <3\pi>2 \pm \alpha`) или (`270^\circ \pm \alpha`):

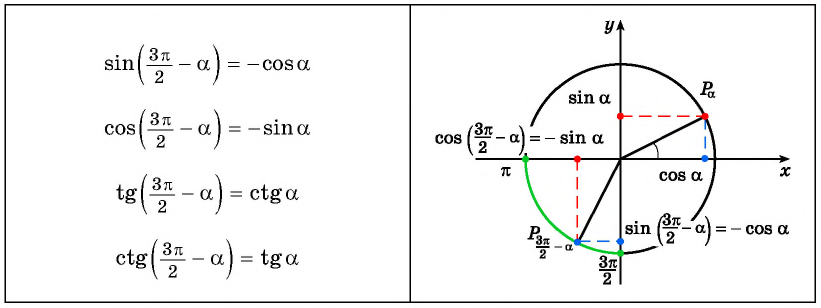
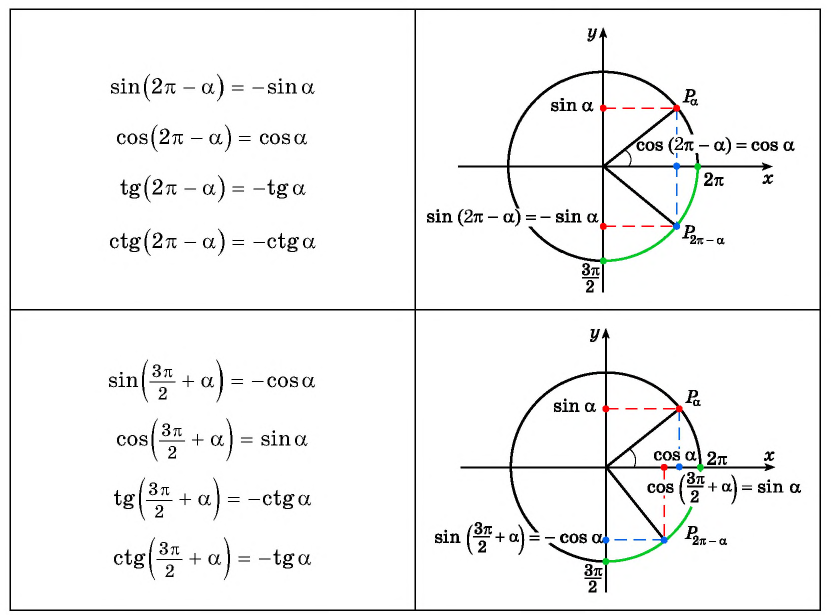
`sin(\frac <3\pi>2 — \alpha)=-cos \ \alpha;` ` sin(\frac <3\pi>2 + \alpha)=-cos \ \alpha`
`cos(\frac <3\pi>2 — \alpha)=-sin \ \alpha;` ` cos(\frac <3\pi>2 + \alpha)=sin \ \alpha`
`tg(\frac <3\pi>2 — \alpha)=ctg \ \alpha;` ` tg(\frac <3\pi>2 + \alpha)=-ctg \ \alpha`
`ctg(\frac <3\pi>2 — \alpha)=tg \ \alpha;` ` ctg(\frac <3\pi>2 + \alpha)=-tg \ \alpha`

Для угла (`2\pi \pm \alpha`) или (`360^\circ \pm \alpha`):

`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`

Часто можно встретить формулы приведения в виде таблицы, где углы записаны в радианах:

Чтобы воспользоваться ею, нужно выбрать строку с нужной нам функцией, и столбец с нужным аргументом. Например, чтобы узнать с помощью таблицы, чему будет равно ` sin(\pi + \alpha)`, достаточно найти ответ на пересечении строки ` sin \beta` и столбца ` \pi + \alpha`. Получим ` sin(\pi + \alpha)=-sin \ \alpha`.

И вторая, аналогичная таблица, где углы записаны в градусах:

Мнемоническое правило формул приведения или как их запомнить

Как мы уже упоминали, заучивать все вышеприведенные соотношения не нужно. Если вы внимательно на них посмотрели, то наверняка заметили некоторые закономерности. Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.

Сразу отметим, что для применения этого правила нужно хорошо уметь определять (или запомнить) знаки тригонометрических функций в разных четвертях единичной окружности.Само привило содержит 3 этапа:

Чтобы посмотреть, как на практике можно применить это правило, преобразим несколько выражений:

Ответ: ` cos(\pi + \alpha)= — cos \alpha`

2. `sin(\frac <3\pi>2 — \alpha)`.

Ответ: `sin(\frac <3\pi>2 — \alpha)= — cos \alpha`

3. `cos(\frac <7\pi>2 — \alpha)`.

`cos(\frac <7\pi>2 — \alpha)=cos(\frac <6\pi>2+\frac <\pi>2-\alpha)=cos (3\pi+(\frac<\pi>2-\alpha))`. Представим `3\pi` как `2\pi+\pi`. `2\pi` — период функции.

Важно: Функции `cos \alpha` и `sin \alpha` имеют период `2\pi` или `360^\circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.

Исходя из этого, наше выражение можно записать следующим образом: `cos (\pi+(\frac<\pi>2-\alpha)`. Применив два раза мнемоническое правило, получим: `cos (\pi+(\frac<\pi>2-\alpha)= — cos (\frac<\pi>2-\alpha)= — sin \alpha`.

Ответ: `cos(\frac <7\pi>2 — \alpha)=- sin \alpha`.

Лошадиное правило

Второй пункт вышеописанного мнемонического правила еще называют лошадиным правилом формул приведения. Интересно, почему лошадиным?

Итак, мы имеем функции с аргументами `\frac <\pi>2 \pm \alpha`, `\pi \pm \alpha`, `\frac <3\pi>2 \pm \alpha`, `2\pi \pm \alpha`, точки `\frac <\pi>2`, `\pi`, `\frac <3\pi>2`, `2\pi` — ключевые, они располагаются на осях координат. `\pi` и `2\pi` на горизонтальной оси абсцисс, а `\frac <\pi>2` и `\frac <3\pi>2` на вертикальной оси ординат.

Задаем себе вопрос: «Меняется ли функция на кофункцию?». Чтобы ответить на этот вопрос, нужно подвигать головой вдоль оси, на которой расположена ключевая точка.

То есть для аргументов с ключевыми точками, расположенными на горизонтальной оси, мы отвечаем «нет», мотая головой в стороны. А для углов с ключевыми точками, расположенными на вертикальной оси, мы отвечаем «да», кивая головой сверху вниз, как лошадь 🙂

Рекомендуем посмотреть видеоурок, в котором автор подробно объясняет, как запомнить формулы приведения без заучивания их наизусть.

Практические примеры использования формул приведения

Применение формул приведения начинается еще в 9, 10 классе. Немало задач с их использованием вынесено на ЕГЭ. Вот некоторые из задач, где придется применять эти формулы:

Пример 1. Вычислите при помощи формул приведения а) `sin 600^\circ`, б) `tg 480^\circ`, в) `cos 330^\circ`, г) `sin 240^\circ`.

Решение: а) `sin 600^\circ=sin (2 \cdot 270^\circ+60^\circ)=-cos 60^\circ=-\frac 1 2`;

б) `tg 480^\circ=tg (2 \cdot 270^\circ-60^\circ)=ctg 60^\circ=\frac<\sqrt 3>3`;

в) `cos 330^\circ=cos (360^\circ-30^\circ)=cos 30^\circ=\frac<\sqrt 3>2`;

г) `sin 240^\circ=sin (270^\circ-30^\circ)=-cos 30^\circ=-\frac<\sqrt 3>2`.

Пример 2. Выразив косинус через синус по формулам приведения, сравнить числа: 1) `sin \frac <9\pi>8` и `cos \frac <9\pi>8`; 2) `sin \frac <\pi>8` и `cos \frac <3\pi>10`.

Решение: 1)`sin \frac <9\pi>8=sin (\pi+\frac <\pi>8)=-sin \frac <\pi>8`

`cos \frac <9\pi>8=cos (\pi+\frac <\pi>8)=-cos \frac <\pi>8=-sin \frac <3\pi>8`

2) `cos \frac <3\pi>10=cos (\frac <\pi>2-\frac <\pi>5)=sin \frac <\pi>5`

`sin \frac <\pi>8 Доказательство формул приведения

Докажем сначала две формулы для синуса и косинуса аргумента `\frac <\pi>2 + \alpha`: ` sin(\frac <\pi>2 + \alpha)=cos \ \alpha` и` cos(\frac <\pi>2 + \alpha)=-sin \ \alpha`. Остальные выводятся из них.

Возьмем единичную окружность и на ней точку А с координатами (1,0). Пусть после поворота на угол `\alpha` она перейдет в точку `А_1(х, у)`, а после поворота на угол `\frac <\pi>2 + \alpha` в точку `А_2(-у,х)`. Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac <\pi>2 + \alpha)=x`, ` cos(\frac <\pi>2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac <\pi>2 + \alpha)=cos \alpha` и ` cos(\frac <\pi>2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac <\pi>2 + \alpha`.

Выходя из определения тангенса и котангенса, получим ` tg(\frac <\pi>2 + \alpha)=\frac 2 + \alpha)>2 + \alpha)>=\frac <-sin \alpha>=-ctg \alpha` и ` сtg(\frac <\pi>2 + \alpha)=\frac 2 + \alpha)>2 + \alpha)>=\frac <-sin \alpha>=-tg \alpha`, что доказывает формулы приведения для тангенса и котангенса угла `\frac <\pi>2 + \alpha`.

Чтобы доказать формулы с аргументом `\frac <\pi>2 — \alpha`, достаточно представить его, как `\frac <\pi>2 + (-\alpha)` и проделать тот же путь, что и выше. Например, `cos(\frac <\pi>2 — \alpha)=cos(\frac <\pi>2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.

Углы `\pi + \alpha` и `\pi — \alpha` можно представить, как `\frac <\pi>2 +(\frac <\pi>2+\alpha)` и `\frac <\pi>2 +(\frac <\pi>2-\alpha)` соответственно.

А `\frac <3\pi>2 + \alpha` и `\frac <3\pi>2 — \alpha` как `\pi +(\frac <\pi>2+\alpha)` и `\pi +(\frac <\pi>2-\alpha)`.

Источник

Формулы приведения с примерами решения

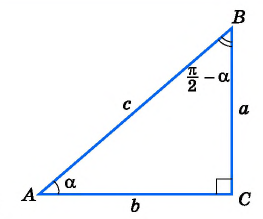
При изучении геометрии вы установили, что

если

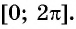
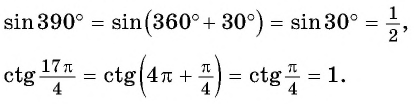
Свойство периодичности тригонометрических функций позволяет свести вычисление значений синуса, косинуса, тангенса и котангенса произвольного угла к вычислению значений этих функций при значениях аргумента, принадлежащих промежутку Например,

На практике принято сводить значения тригонометрических функций произвольного угла к вычислению значений этих функций для угла, принадлежащего промежутку .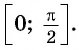

Это можно делать с помощью формул приведения.

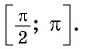
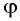
Рассмотрим промежуток Любое число из этого промежутка можно пред ставить в виде

Например,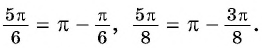
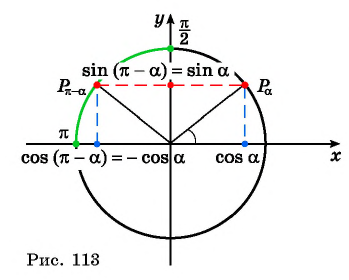
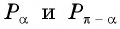
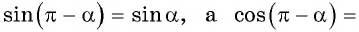
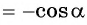
Поскольку ординаты точек равны, а абсциссы отличаются только знаком, то: (рис. 113).
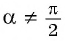
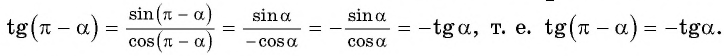
Тогда для получим, что
А для 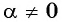имеем:

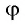
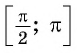
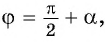
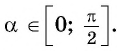
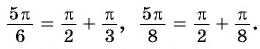
Вместе с тем любое число из промежутка можно также представить в виде где Например,
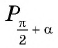
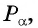
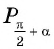
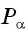
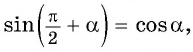
Так как ордината точки равна абсциссе точки а абсцисса точки отличается от ординаты точки только знаком (рис. 114), то: а

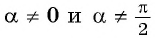
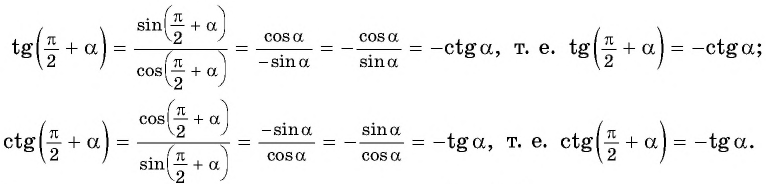
Для получим:

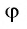
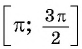
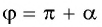
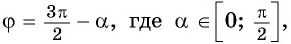
Так как любое число из промежутка можно представить в виде или то, рассуждая аналогично, получим формулы приведения:

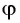
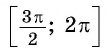
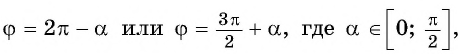
Поскольку любое число из промежутка можно представить в виде то получим:

Проанализировав полученные формулы, можно заметить закономерности, позволяющие сформулировать правило, с помощью которого можно применять формулы приведения, не заучивая их:

В правой части формулы приведения ставится тот знак, который имеет в соответствующей четверти исходная функция, если считать, что угол 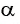— острый.

Если в формуле приведения аргумент имеет вид:

Например, применим полученное правило для выражения

Пример:

Приведите выражение к тригонометрической функции числа 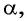применив формулы приведения:

Решение:

а) 1. Так как 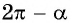— угол четвертой четверти, в которой косинус положительный, то в правой части равенства не нужно ставить знак «минус».

2. Поскольку аргумент имеет вид 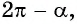то название функции «косинус» не меняется. Значит,

б) 1. Так как 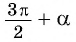— угол четвертой четверти, в которой тангенс отрицательный, то в правой части равенства нужно поставить знак «минус».

2.Поскольку аргумент имеет вид 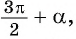название функции «тангенс» нужно поменять на «котангенс». Тогда

в) 1. Так как 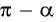— угол второй четверти, в которой синус положительный, то в правой части равенства части равенства не нужно ставить знак «минус»

2. Поскольку аргумент имеет вид 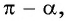то название функции «синус» не меняется. Значит,

Пример:

Используйте формулы приведения и найдите значение выражения:

Решение:

Первый способ:

Второй способ:

(в третьей четверти тангенс положительный, название функции не меняется).

(в третьей четверти косинус отрицательный, название функции не меняется). (в четвертой четверти котангенс отрицательный, название функции не меняется).

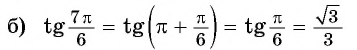
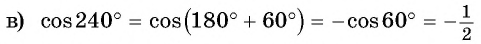
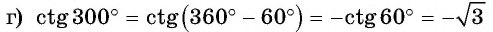
Пример:

Вычислите, используя формулы приведения:

Решение:

(в четвертой четверти косинус положительный, название функции не меняется);

(во второй четверти синус положительный, название функции не меняется);

(в третьей четверти котангенс положительный, название функции меняется);

(в четвертой четверти тангенс отрицательный, название функции не меняется).

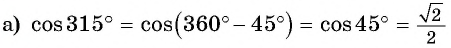
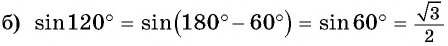
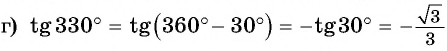
Пример:

Найдите значение выражения:

Решение:

а) Так как синус — нечетная функция, то

Применим формулы приведения:

б) Воспользуемся свойством четности косинуса и получим:

По формулам приведения:

в) Воспользуемся свойством периодичности тангенса и получим:

Применим формулы приведения:

г) Поскольку котангенс — нечетная функция, то

Используем свойство периодичности котангенса и получим:

Пример:

По формулам приведения:

Приведите к тригонометрической функции угла

Решение:

а) Используем свойство периодичности косинуса и получим:

По формулам приведения:

б) Воспользуемся свойством периодичности котангенса:

Применим формулы приведения:

в) Так как тангенс — нечетная функция, то 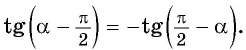По формулам приведения:

г) Поскольку синус — нечетная функция, то

Воспользуемся свойством периодичности синуса и получим:

По формулам приведения:

Пример:

Приведите к тригонометрической функции угла

Решение:

Пример:

Решение:

Пример:

Решение:

а) Применим формулы приведения:

б)Воспользуемся периодичностью косинуса и формулами приведения и получим:

в)Применим формулы приведения:

г) Используем периодичность тангенса, нечетность котангенса и формулы приведения:

Пример:

Решите уравнение:

Решение:

Применим формулы приведения и получим:

Ответ:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник